Section 4.4 – Sum-to-Product and Product-to-Sum Formulas
Learning Objectives
Welcome to Section 4.4! In this section you will…
- Express products as sums.
- Express sums as products.

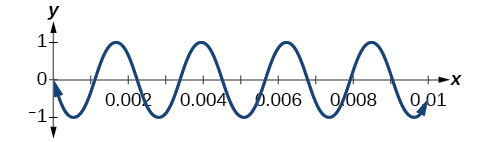
A band marches down the street creating an amazing sound that bolsters the crowd. That sound travels as a wave that can be interpreted using trigonometric functions. For example, Figure 2 represents a sound wave for the musical note A. In this section, we will investigate trigonometric identities that are the foundation of everyday phenomena such as sound waves.
Expressing Products as Sums
We have already learned a number of formulas useful for expanding or simplifying trigonometric expressions, but sometimes we may need to express the product of cosine and sine as a sum. We can use the product-to-sum formulas, which express products of trigonometric functions as sums. Let’s investigate the cosine identity first and then the sine identity.
Expressing Products as Sums for Cosine
We can derive the product-to-sum formula from the sum and difference identities for cosine. If we add the two equations, we get:
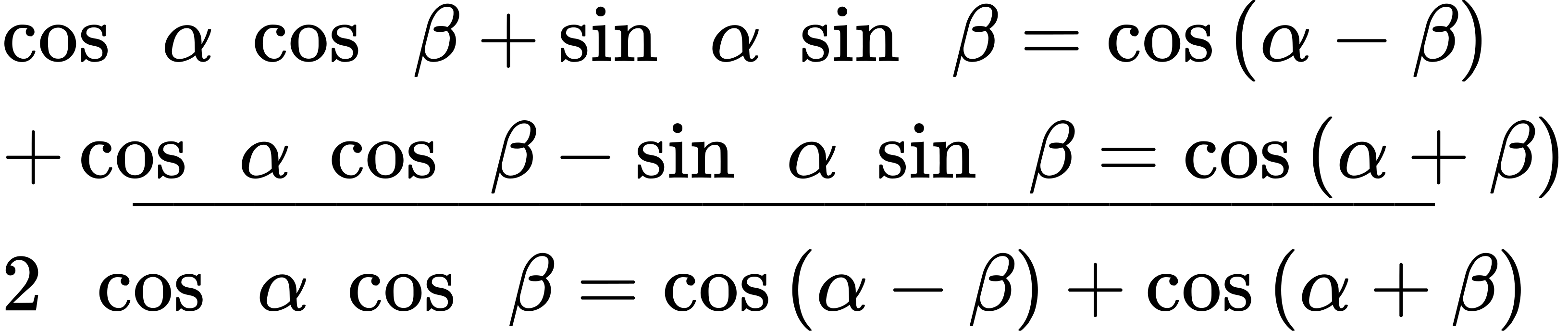
Then, we divide by 2 to isolate the product of cosines:
How To
Given a product of cosines, express as a sum.
- Write the formula for the product of cosines.
- Substitute the given angles into the formula.
- Simplify.
Example 1
Writing the Product as a Sum Using the Product-to-Sum Formula for Cosine
Write the following product of cosines as a sum: 2 [latex]cos[/latex] ([latex]\frac{7x}{2}[/latex]) [latex]cos[/latex] ([latex]\frac{3x}{2}[/latex]).
Show/Hide Solution
Solution
We begin by writing the formula for the product of cosines:
[latex]cos[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] = [latex]\dfrac{1}{2}[/latex][[latex]cos[/latex] ([latex]α[/latex] − [latex]β[/latex]) + [latex]cos[/latex] ([latex]α[/latex] + [latex]β[/latex])]
We can then substitute the given angles into the formula and simplify.
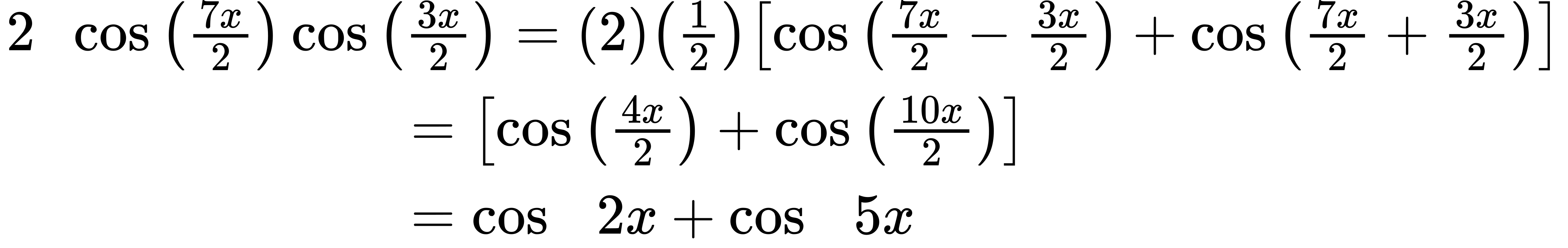
Try It #1
Use the product-to-sum formula to write the product as a sum or difference:
[latex]cos[/latex] ([latex]2θ[/latex]) [latex]cos[/latex] ([latex]4θ[/latex])
Expressing the Product of Sine and Cosine as a Sum
Next, we will derive the product-to-sum formula for sine and cosine from the sum and difference formulas for sine. If we add the sum and difference identities, we get:
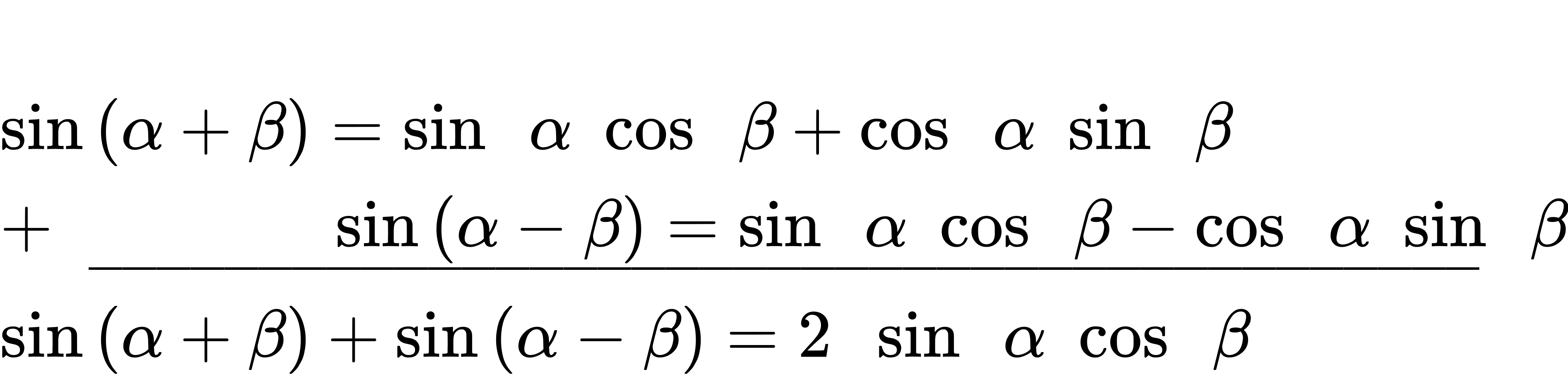
Then, we divide by 2 to isolate the product of cosine and sine:
[latex]sin[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] = [latex]\dfrac{1}{2}[/latex][latex][sin(α − β) + sin(α+ β)][/latex]
Example 2
Writing the Product as a Sum Containing only Sine or Cosine
Express the following product as a sum containing only sine or cosine and no products:
[latex]sin (4θ)[/latex] [latex]cos (2θ)[/latex]
Show/Hide Solution
Solution
Write the formula for the product of sine and cosine. Then substitute the given values into the formula and simplify.
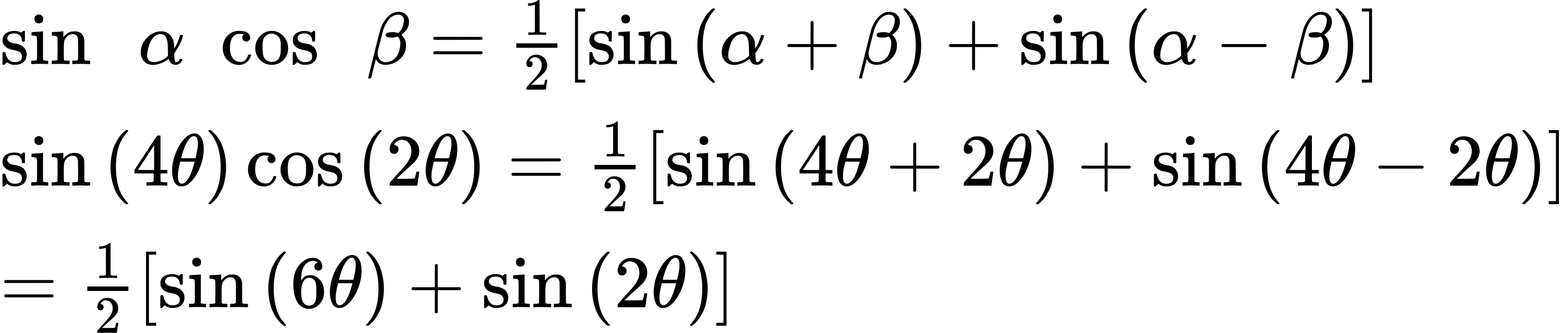
Try It #2
Use the product-to-sum formula to write the following product as a sum containing only sine or cosine: [latex]sin(x + y)[/latex] [latex]cos(x − y)[/latex].
Expressing Products of Sines in Terms of Cosine
Expressing the product of sines in terms of cosine is also derived from the sum and difference identities for cosine. In this case, we will first subtract the two cosine formulas:
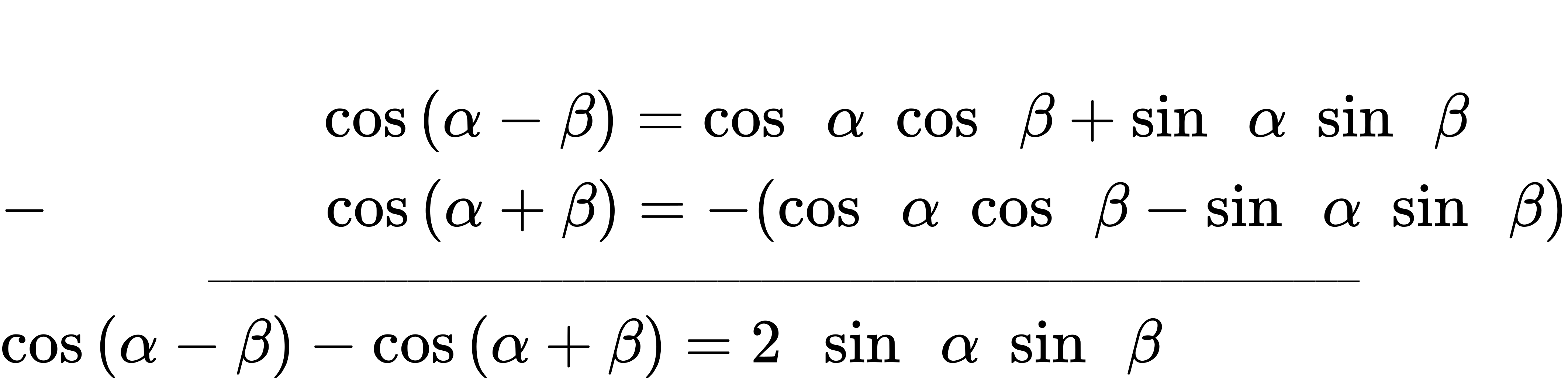
Then, we divide by 2 to isolate the product of sines:
[latex]sin[/latex] [latex]α[/latex] [latex]sin[/latex] [latex]β[/latex] = [latex]\dfrac{1}{2}[/latex][[latex]cos[/latex] ([latex]α[/latex] − [latex]β[/latex]) − [latex]cos[/latex] ([latex]α[/latex] + [latex]β[/latex])]
Similarly we could express the product of cosines in terms of sine or derive other product-to-sum formulas.
The Product-to-Sum Formulas
The product-to-sum formulas are as follows:
Example 3
Express the Product as a Sum or Difference
Write [latex]cos[/latex] ([latex]3θ[/latex]) [latex]cos[/latex] ([latex]5θ[/latex]) as a sum or difference.
Show/Hide Solution
Solution
We have the product of cosines, so we begin by writing the related formula. Then we substitute the given angles and simplify.
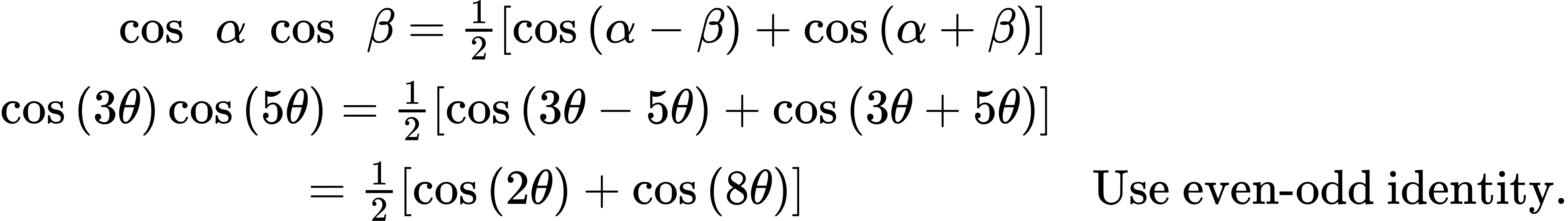
Try It #3
Use the product-to-sum formula to evaluate [latex]cos[/latex] ([latex]\frac{11π}{12}[/latex]) [latex]cos[/latex] ([latex]\frac{π}{12}[/latex]).
Expressing Sums as Products
Some problems require the reverse of the process we just used. The sum-to-product formulas allow us to express sums of sine or cosine as products. These formulas can be derived from the product-to-sum identities. For example, with a few substitutions, we can derive the sum-to-product identity for sine. Let [latex]\frac{u + v}{2}[/latex] = [latex]α[/latex] and [latex]\frac{u − v}{2}[/latex] = [latex]β[/latex].
Then,
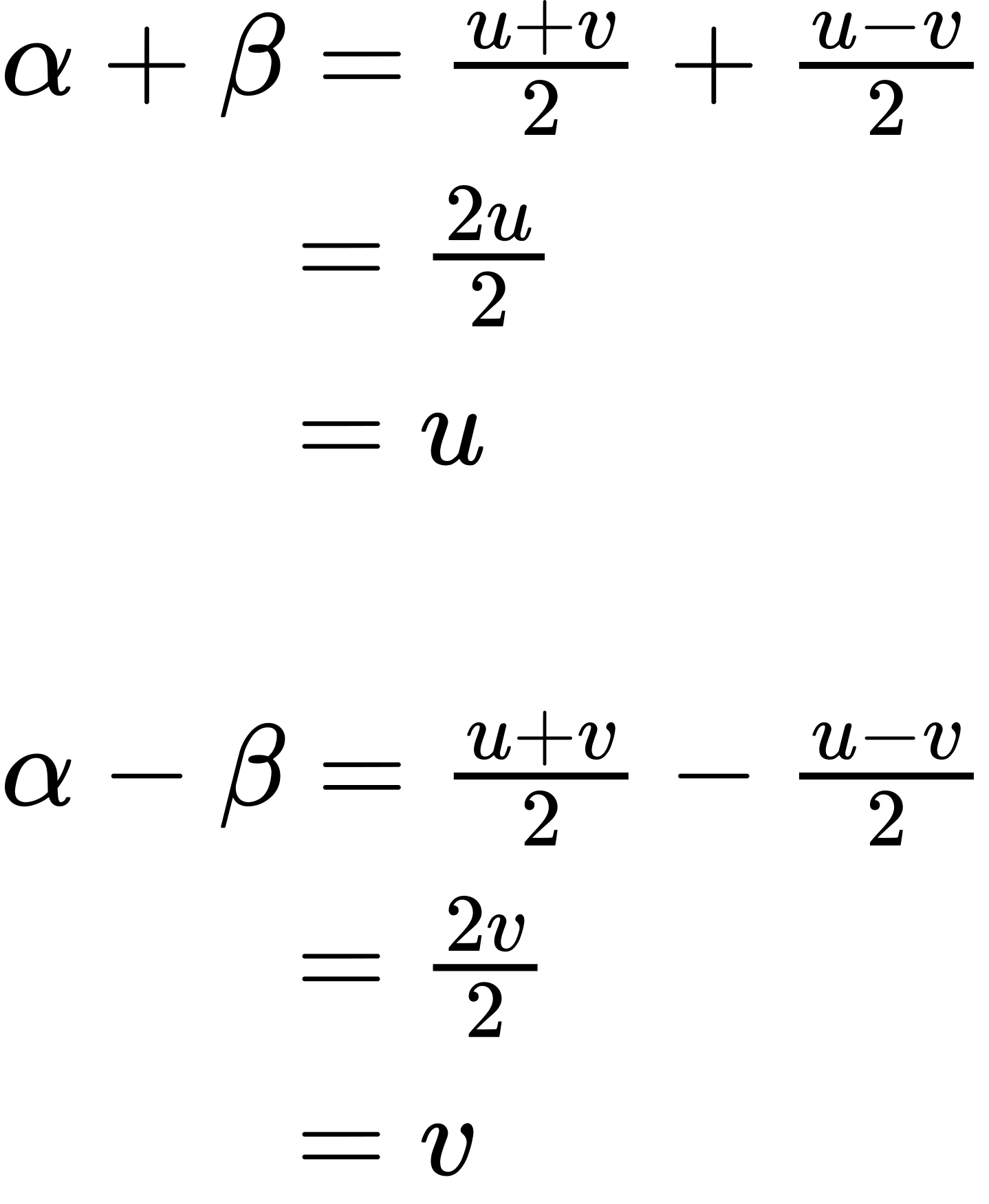
Thus, replacing [latex]α[/latex] and [latex]β[/latex] in the product-to-sum formula with the substitute expressions, we have
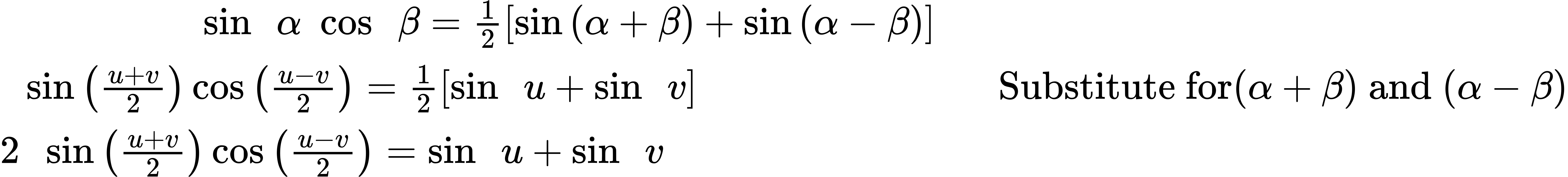
The other sum-to-product identities are derived similarly.
Sum-to-Product Formulas
The sum-to-product formulas are as follows:
Example 4
Writing the Difference of Sines as a Product
Write the following difference of sines expression as a product: [latex]sin[/latex] ([latex]4θ[/latex]) − [latex]sin[/latex] ([latex]2θ[/latex]).
Show/Hide Solution
Solution
We begin by writing the formula for the difference of sines.
[latex]sin[/latex] [latex]α[/latex] − [latex]sin[/latex] [latex]β[/latex] = 2 [latex]sin[/latex] ([latex]\dfrac{α − β}{2}[/latex]) [latex]cos[/latex] ([latex]\dfrac{α + β}{2}[/latex])
Substitute the values into the formula, and simplify.
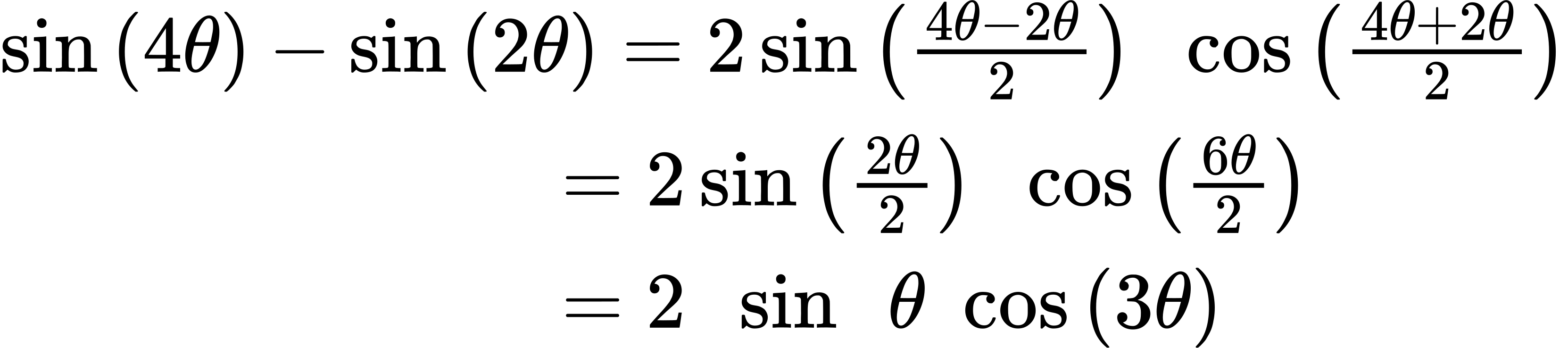
Try It #4
Use the sum-to-product formula to write the sum as a product: [latex]sin[/latex] ([latex]3θ[/latex]) + [latex]sin[/latex] ([latex]θ[/latex]).
Example 5
Evaluating Using the Sum-to-Product Formula
Evaluate [latex]cos[/latex] (15°) − [latex]cos[/latex] (75°).
Show/Hide Solution
Solution
We begin by writing the formula for the difference of cosines.
[latex]cos[/latex] [latex]α[/latex] − [latex]cos[/latex] [latex]β[/latex] = −2 [latex]sin[/latex] ([latex]\dfrac{α + β}{2}[/latex]) [latex]sin[/latex] ([latex]\dfrac{α − β}{2}[/latex])
Then we substitute the given angles and simplify.
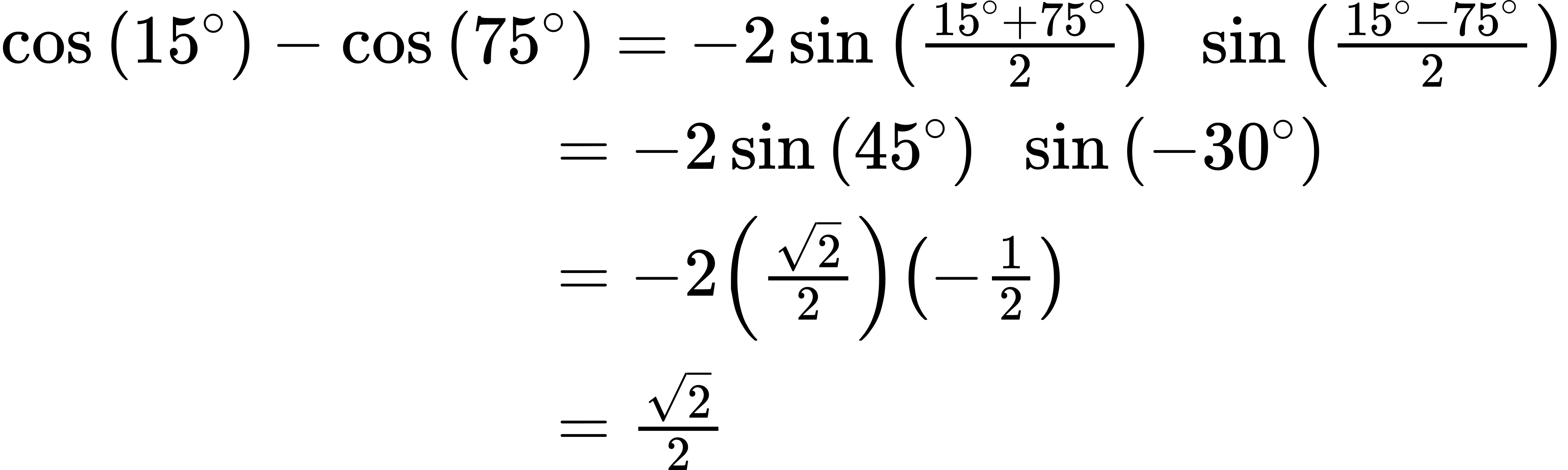
Example 6
Proving an Identity
Prove the identity:
Show/Hide Solution
Solution
We will start with the left side, the more complicated side of the equation, and rewrite the expression until it matches the right side.
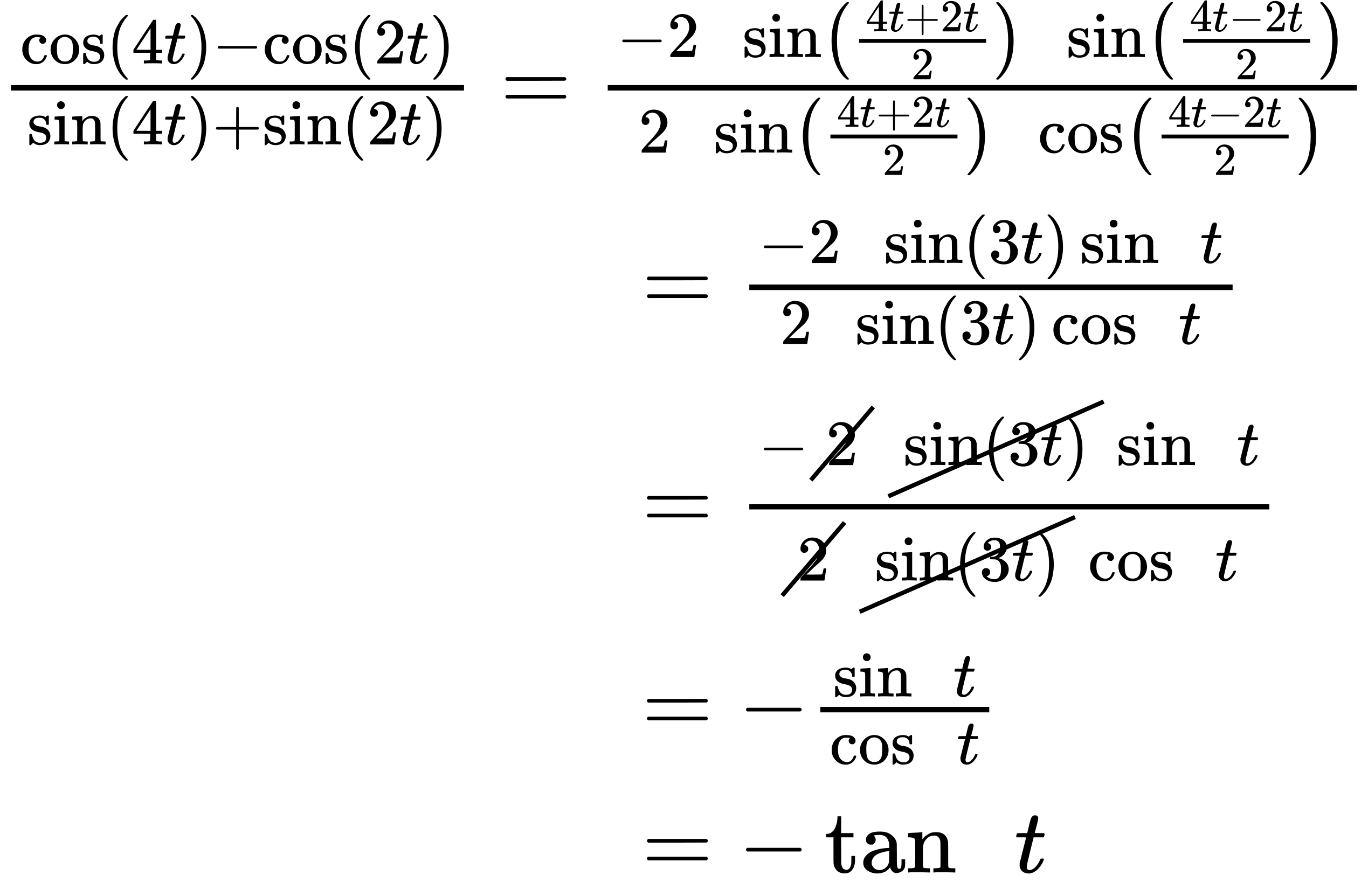
Analysis
Recall that verifying trigonometric identities has its own set of rules. The procedures for solving an equation are not the same as the procedures for verifying an identity. When we prove an identity, we pick one side to work on and make substitutions until that side is transformed into the other side.
Example 7
Verifying the Identity Using Double-Angle Formulas and Reciprocal Identities
Verify the identity.
Show/Hide Solution
Solution
For verifying this equation, we are bringing together several of the identities. We will use the double-angle formula and the reciprocal identities. We will work with the right side of the equation and rewrite it until it matches the left side.
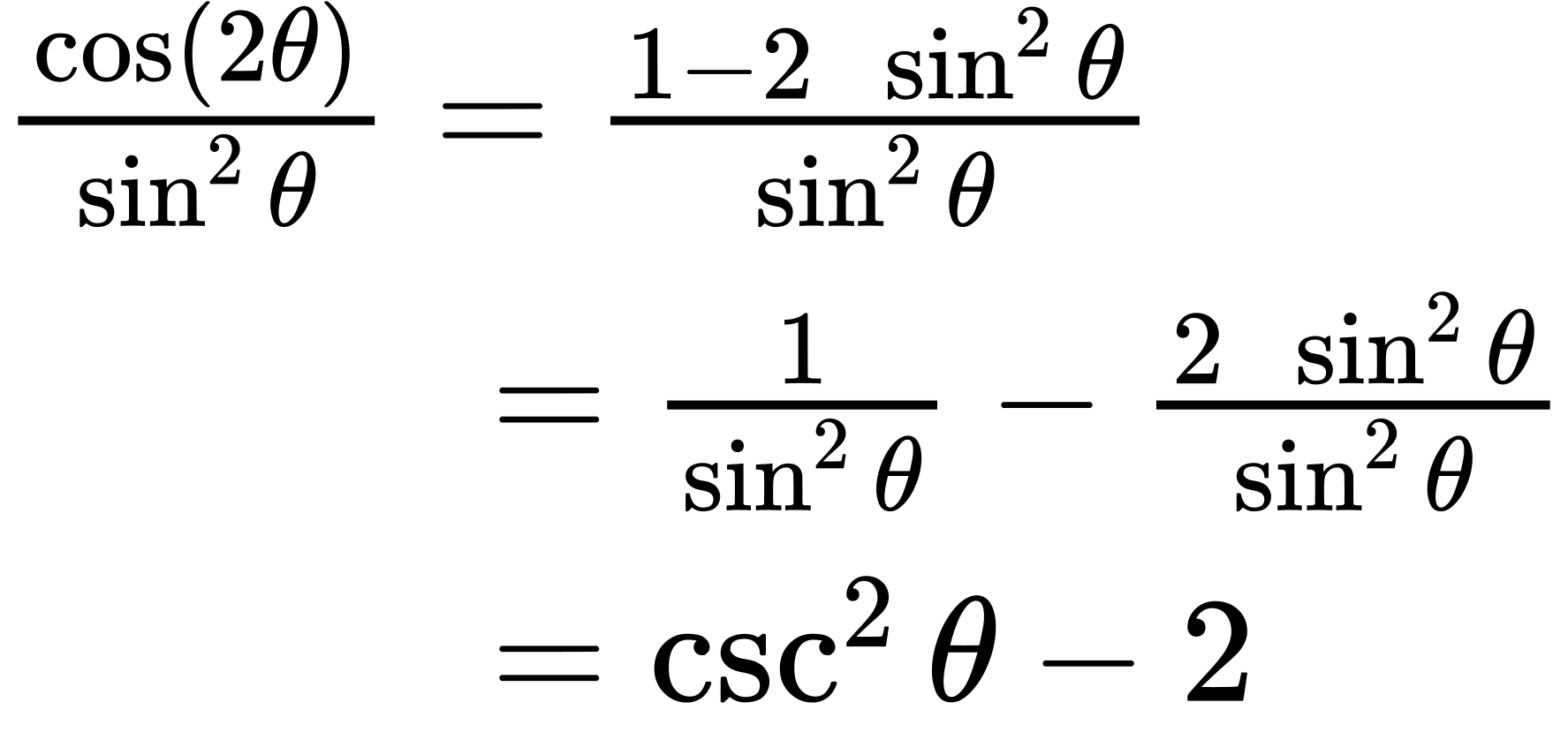
Try It #5
Verify the identity [latex]tan[/latex] [latex]θ[/latex] [latex]cot[/latex] [latex]θ[/latex] − [latex]cos^2[/latex] [latex]θ[/latex] = [latex]sin^2[/latex] [latex]θ[/latex].
Media
Access these online resources for additional instruction and practice with the product-to-sum and sum-to-product identities.
Section Exercises
Verbal
1. Starting with the product to sum formula, [latex]sin[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] = [latex]\dfrac{1}{2}[/latex][[latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]) + [latex]sin[/latex] ([latex]α[/latex] − [latex]β[/latex])], explain how to determine the formula for [latex]cos[/latex] [latex]α[/latex] [latex]sin[/latex] [latex]β[/latex].
2. Explain two different methods of calculating [latex]cos[/latex] (195°) [latex]cos[/latex] (105°), one of which uses the product to sum. Which method is easier?
3. Explain a situation where we would convert an equation from a sum to a product and give an example.
4. Explain a situation where we would convert an equation from a product to a sum and give an example.
Algebraic
For the following exercises, rewrite the product as a sum or difference.
5. 16 [latex]sin[/latex] ([latex]16x[/latex]) [latex]sin[/latex] ([latex]11x[/latex])
6. 20 [latex]cos[/latex] ([latex]36t[/latex]) [latex]cos[/latex] ([latex]6t[/latex])
7. 2 [latex]sin[/latex] ([latex]5x[/latex]) [latex]cos[/latex] ([latex]3x[/latex])
8. 10 [latex]cos[/latex] ([latex]5x[/latex]) [latex]sin[/latex] ([latex]10x[/latex])
9. [latex]sin[/latex] (−[latex]x[/latex]) [latex]sin[/latex] ([latex]5x[/latex])
10. [latex]sin[/latex] ([latex]3x[/latex]) [latex]cos[/latex] ([latex]5x[/latex])
For the following exercises, rewrite the sum or difference as a product.
11. [latex]cos[/latex] ([latex]6t[/latex]) + [latex]cos[/latex] ([latex]4t[/latex])
12. [latex]sin[/latex] ([latex]3x[/latex]) + [latex]sin[/latex] ([latex]7x[/latex])
13. [latex]cos[/latex] ([latex]7x[/latex]) + [latex]cos[/latex] ([latex]−7x[/latex])
14. [latex]sin[/latex] ([latex]3x[/latex]) − [latex]sin[/latex] ([latex]−3x[/latex])
15. [latex]cos[/latex] ([latex]3x[/latex]) + [latex]cos[/latex] ([latex]9x[/latex])
16. [latex]sin[/latex] [latex]h[/latex] − [latex]sin[/latex] ([latex]3h[/latex])
For the following exercises, evaluate the product for the following using a sum or difference of two functions.
17. [latex]cos[/latex] (45°) [latex]cos[/latex] (15°)
18. [latex]cos[/latex] (45°) [latex]sin[/latex] (15°)
19. [latex]sin[/latex] (−345°) [latex]sin[/latex] (−15°)
20. [latex]sin[/latex] (195°) [latex]cos[/latex] (15°)
21. [latex]sin[/latex] (−45°) [latex]sin[/latex] (−15°)
For the following exercises, evaluate the product using a sum or difference of two functions. Leave in terms of sine and cosine.
22. [latex]cos[/latex] (23°) [latex]sin[/latex] (17°)
23. 2 [latex]sin[/latex] (100°) [latex]sin[/latex] (20°)
24. 2 [latex]sin[/latex] (−100°) [latex]sin[/latex] (−20°)
25. [latex]sin[/latex] (213°) [latex]cos[/latex] (8°)
26. 2 [latex]cos[/latex] (56°) [latex]cos[/latex] (47°)
For the following exercises, rewrite the sum as a product of two functions. Leave in terms of sine and cosine.
27. [latex]sin[/latex] (76°) + [latex]sin[/latex] (14°)
28. [latex]cos[/latex] (58°) − [latex]cos[/latex] (12°)
29. [latex]sin[/latex] (101°) − [latex]sin[/latex] (32°)
30. [latex]cos[/latex] (100°) + [latex]cos[/latex] (200°)
31. [latex]sin[/latex] (−1°) + [latex]sin[/latex] (−2°)
For the following exercises, prove the identity.
32. [latex]\frac{cos (a + b)}{cos (a − b)}[/latex] = [latex]\frac{1 − tan a tan b}{1 + tan a tan b}[/latex]
33. 4 [latex]sin[/latex] ([latex]3x[/latex]) [latex]cos[/latex] ([latex]4x[/latex]) = 2 [latex]sin[/latex] ([latex]7x[/latex]) − 2 [latex]sin[/latex] [latex]x[/latex]
34. [latex]\frac{6 cos (8x) sin (2x)}{sin (−6x)}[/latex] = −3 [latex]sin[/latex] ([latex]10x[/latex]) [latex]csc[/latex] ([latex]6x[/latex]) +3
35. [latex]sin[/latex] [latex]x[/latex] + [latex]sin[/latex] ([latex]3x[/latex])= 4 [latex]sin[/latex] [latex]x[/latex] [latex]cos^2[/latex] [latex]x[/latex]
36. 2 ([latex]cos^3[/latex] [latex]x[/latex] − [latex]cos[/latex] [latex]x[/latex] [latex]sin^2[/latex] [latex]x[/latex]) = [latex]cos[/latex] ([latex]3x[/latex]) + [latex]cos[/latex] [latex]x[/latex]
37. 2 [latex]tan[/latex] [latex]x[/latex] [latex]cos[/latex] ([latex]3x[/latex]) = [latex]sec[/latex] [latex]x[/latex] ([latex]sin[/latex] ([latex]4x[/latex]) − [latex]sin[/latex] ([latex]2x[/latex]))
38. [latex]cos[/latex] ([latex]a[/latex] + [latex]b[/latex]) + [latex]cos[/latex] ([latex]a[/latex] − [latex]b[/latex]) = 2 [latex]cos[/latex] [latex]a[/latex] [latex]cos[/latex] [latex]b[/latex]
Numeric
For the following exercises, rewrite the sum as a product of two functions or the product as a sum of two functions. Give your answer in terms of sines and cosines. Then evaluate the final answer numerically, rounded to four decimal places.
39. [latex]cos[/latex] (58°) + [latex]cos[/latex] (12°)
40. [latex]sin[/latex] (2°) − [latex]sin[/latex] (3°)
41. [latex]cos[/latex] (44°) − [latex]cos[/latex] (22°)
42. [latex]cos[/latex] (176°) [latex]sin[/latex] (9°)
43. [latex]sin[/latex] (−14°) [latex]sin[/latex] (85°)
Extensions
For the following exercises, prove the following sum-to-product formulas.
44. [latex]sin[/latex] [latex]x[/latex] − [latex]sin[/latex] [latex]y[/latex] = 2 [latex]sin[/latex] ([latex]\frac{x − y}{2}[/latex]) [latex]cos[/latex] ([latex]\frac{x + y}{2}[/latex])
45. [latex]cos[/latex] [latex]x[/latex] + [latex]cos[/latex] [latex]y[/latex] = 2 [latex]cos[/latex] ([latex]\frac{x + y}{2}[/latex]) [latex]cos[/latex] ([latex]\frac{x − y}{2}[/latex])
For the following exercises, prove the identity.
46. [latex]\frac{sin (6x) + sin(4x)}{sin (6x) − sin (4x)}[/latex]= [latex]tan[/latex] ([latex]5x[/latex]) [latex]cot[/latex] [latex]x[/latex]
47. [latex]\frac{cos (3x) + cos x}{cos (3x) − cos x}[/latex]= −[latex]cot[/latex] ([latex]2x[/latex]) [latex]cot[/latex] [latex]x[/latex]
48. [latex]\frac{cos (6y) + cos (8y)}{sin (6y) − sin (4y)}[/latex]= [latex]cot[/latex] [latex]y[/latex] [latex]cos[/latex] ([latex]7y[/latex]) [latex]sec[/latex] ([latex]5y[/latex])
49. [latex]\frac{cos (2y) − cos (4y)}{sin (2y) + sin (4y)}[/latex]= [latex]tan[/latex] [latex]y[/latex]
50. [latex]\frac{sin (10x) − sin (2x)}{cos (10x) + cos (2x)}[/latex]= [latex]tan[/latex] ([latex]4x[/latex])
51. [latex]cos[/latex] [latex]x[/latex] − [latex]cos[/latex] ([latex]3x[/latex]) = 4 [latex]sin^2[/latex] [latex]x[/latex] [latex]cos[/latex] [latex]x[/latex]
52. ([latex]cos[/latex] ([latex]2x[/latex]) − [latex]cos[/latex] ([latex]4x[/latex]))2 + ([latex]sin[/latex] ([latex]4x[/latex]) + [latex]sin[/latex] ([latex]2x[/latex]))2 = 4 [latex]sin^2[/latex] ([latex]3x[/latex])
53. tan([latex]\frac{π}{4}[/latex]− t) = [latex]\frac{1 − tan t}{1 + tan t}[/latex]

