Chapter 3 – Periodic Functions
"Try It" Exercises
Section 3.1 - Graphs of the Sine and Cosine Functions
1. 6π
2. [latex]\frac{1}{2}[/latex] compressed
3. [latex]\frac{π}{2}[/latex]; right
4. 2 units up
5.
midline: y=0; amplitude: |A|=12; period: [latex]P=\frac{2π}{|B|}=6π[/latex]; phase shift: [latex]\frac{C}{B}[/latex]=π
6. f(x)=sin(x)+2
7. two possibilities: [latex]y=4sin(\frac{π}{5}x−\frac{π}{5}+4)[/latex] or [latex]y=−4sin(\frac{π}{5}x+\frac{4π}{5}+4)[/latex]
8.
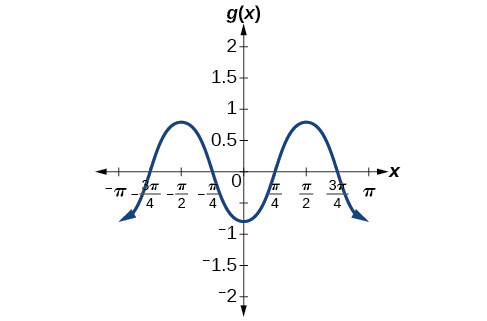
midline: y=0; amplitude: |A|=0.8; period: [latex]P=\frac{2π}{|B|}=π[/latex]; phase shift: [latex]\frac{C}{B}=0[/latex] or none
9.
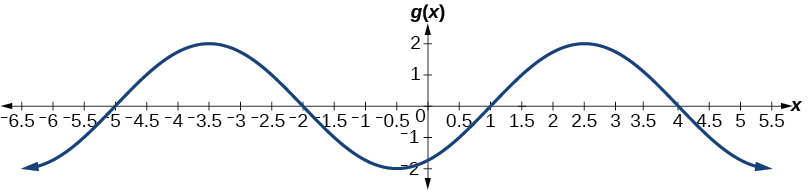
midline: y=0; amplitude: |A|=2; period: [latex]P=\frac{2π}{|B|}=6[/latex]; phase shift: [latex]\frac{C}{B}=−12[/latex]
10. 7
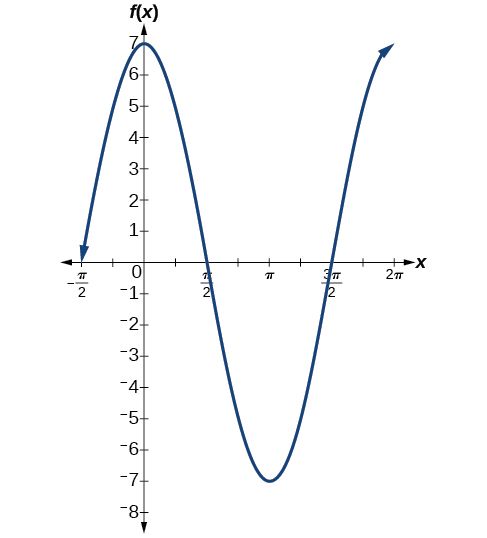
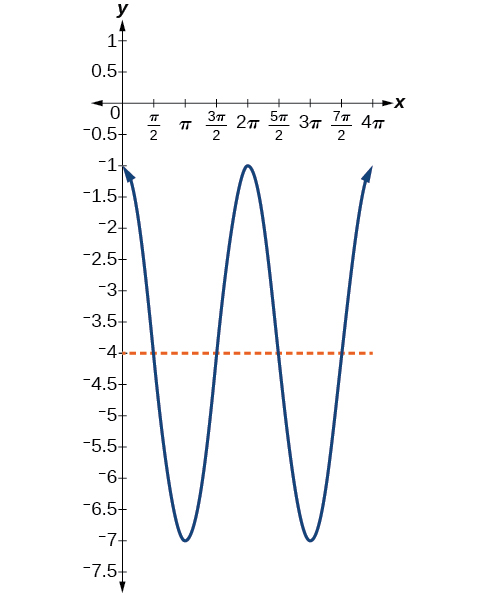
11. y=3cos(x)−4
Section 3.2 - Graphs of the Other Trigonometric Functions
1.
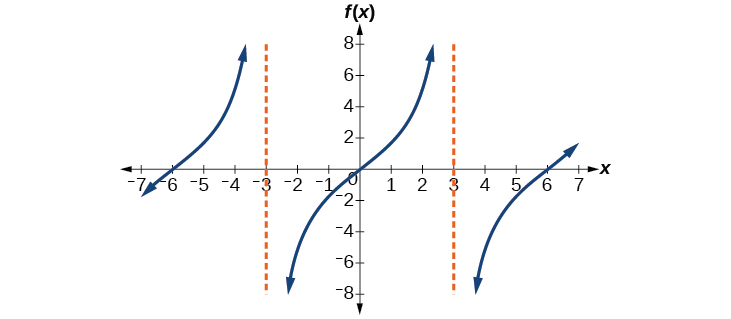
2. It would be reflected across the line y=−1, becoming an increasing function.
3. g(x)=4tan(2x)
4. This is a vertical reflection of the preceding graph because A is negative.
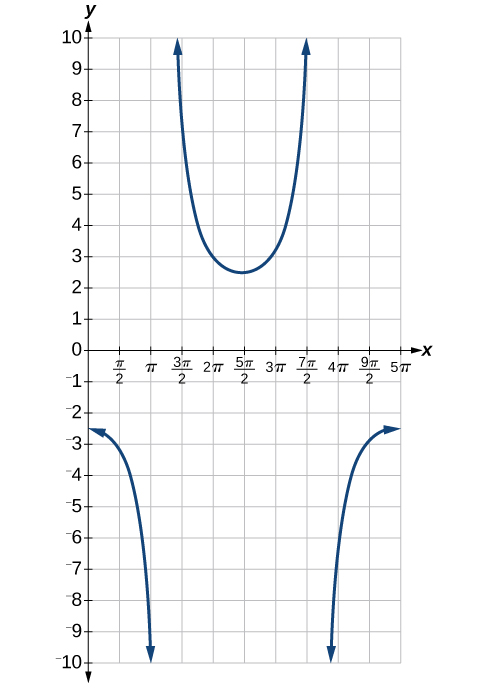
5.
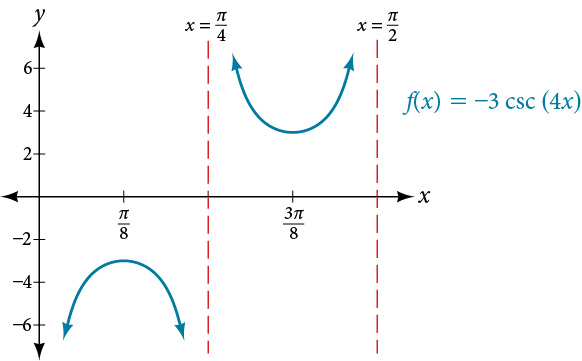
6.
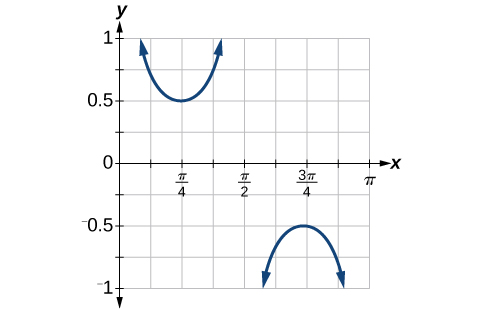
7.
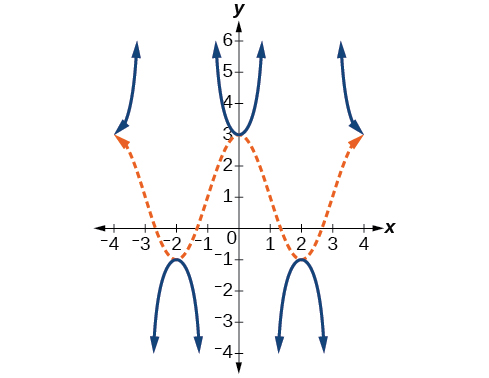
Section 3.3 - Inverse Functions
1. h(2)=6
2. No
3. Yes
4. The domain of function [latex]f^{−1}[/latex] is (−∞,−2) and the range of function [latex]f^{−1}[/latex] is (1,∞).
5.
- ⓐ f(60)=50. In 60 minutes, 50 miles are traveled.
- ⓑ[latex]f^{−1}(60)[/latex]=70. To travel 60 miles, it will take 70 minutes.
6. a. 3; b. 5.6
7. x=3y+5
8. [latex]f^{−1}(x)=(2−x)^2[/latex]; domain of f: [0,∞); domain of f−1: (−∞,2]
9.
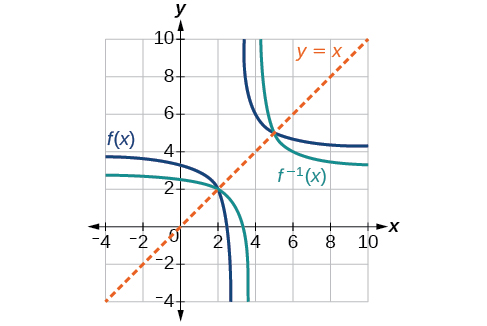
Section 3.4 - Inverse Trigonometric Functions
1. arccos(0.8776)≈0.5
2.
ⓐ [latex]−\frac{π}{2}[/latex];
ⓑ [latex]−\frac{π}{4}[/latex];
ⓒ π;
ⓓ [latex]\frac{π}{3}[/latex]
3. 1.9823 or 113.578°
4. [latex]sin^{−1}(0.6)=36.87∘=0.6435[/latex] radians
5. [latex]\frac{π}{8};\frac{2π}{9}[/latex]
6. [latex]\frac{3π}{4}[/latex]
7. [latex]\frac{12}{13}[/latex]
8. [latex]\frac{4\sqrt{2}}{9}[/latex]
9. [latex]\frac{4x}{\sqrt{16x^2+1}}[/latex]
Section Exercises
Section 3.1 - Graphs of the Sine and Cosine Functions
1. The sine and cosine functions have the property that f(x+P)=f(x) for a certain P. This means that the function values repeat for every P units on the x-axis.
3. The absolute value of the constant A (amplitude) increases the total range and the constant D (vertical shift) shifts the graph vertically.
5. At the point where the terminal side of t intersects the unit circle, you can determine that the sin t equals the y-coordinate of the point.
7.
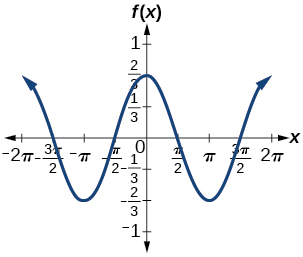
amplitude: [latex]\frac{2}{3}[/latex]; period: 2π; midline: y=0; maximum: [latex]y=\frac{2}{3}[/latex] occurs at x=0; minimum: [latex]y=-\frac{2}{3}[/latex] occurs at x=π; for one period, the graph starts at 0 and ends at 2π
9.
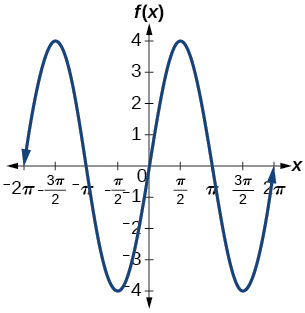
amplitude: 4; period 2π; midline: y=0; maximum y=4 occurs at [latex]x=\frac{π}{2}[/latex]; minimum: y=−4 occurs at [latex]x=\frac{3π}{2}[/latex]; one full period occurs from x=0 to x=2π
11.
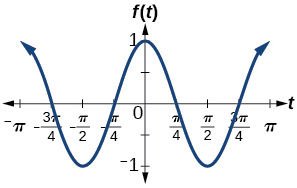
amplitude: 1; period π; midline: y=0; maximum: y=1 occurs at x=π; minimum: y=−1 occurs at [latex]x=\frac{π}{2}[/latex]; one full period is graphed from x=0 to x=π
13.
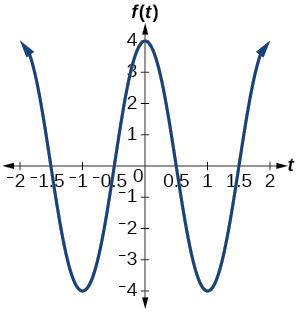
amplitude: 4; period: 2; midline y=0; maximum: y=4 occurs at x=0; minimum: y=−4 occurs at x=1
15.
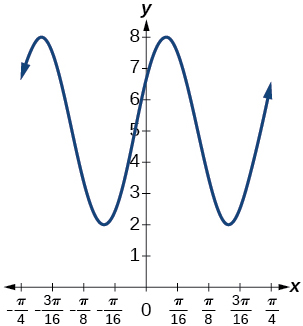
amplitude: 3; period [latex]\frac{π}{4}[/latex]; midline: y=5; maximum: y=8 occurs at x=0.12; minimum: y=2 occurs at x=0.516; horizontal shift: −4; vertical translation 5; one period occurs from x=0 to [latex]x=\frac{π}{4}[/latex]
17.
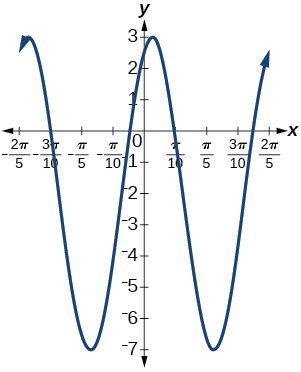
amplitude: 5; period [latex]\frac{2π}{5}[/latex]; midline: y=−2; maximum: y=3 occurs at x=0.08; minimum: y=−7 occurs at x=0.71; phase shift: −4; vertical translation: −2; one full period can be graphed on x=0 to x=[latex]\frac{2π}{5}[/latex]
19.
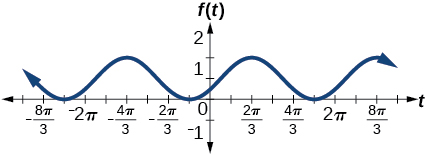
amplitude: 1 ; period 2π; midline: y=1; maximum: y=2 occurs at x=2.09; maximum: y=2 occurs at t=2.09; minimum: y=0 occurs at t=5.24; phase shift: [latex]−\frac{π}{3}[/latex]; vertical translation: 1; one full period is from t=0 to t=2π
21.
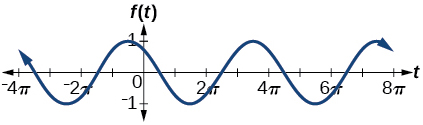
amplitude: 1; period 4π; midline: y=0; maximum: y=1 occurs at t=11.52; minimum: y=−1 occurs at t=5.24; phase shift: [latex]-\frac{10π}{3}[/latex]; vertical shift: 0
23. amplitude: 2; midline: y=−3; period: 4; equation: [latex]f(x)=2sin(\frac{π}{2}x)−3[/latex]
25. amplitude: 2; period: 5; midline: y=3; equation: [latex]f(x)=−2cos(\frac{2π}{5}x)+3[/latex]
27. amplitude: 4; period: 2; midline: y=0; equation: [latex]f(x)=−4cos(π(x−\frac{π}{2})[/latex]
29. amplitude: 2; period: 2; midline: y=1; equation: [latex]f(x)=2cos(πx)+1[/latex]
31. 0,π
33. [latex]sin(\frac{π}{2})=1[/latex]
35. [latex]\frac{π}{2}[/latex]
37. f(x)=sin(x) is symmetric
39. [latex]\frac{π}{3}[/latex],[latex]\frac{5π}{3}[/latex]
41. Maximum: 1 at x=0 ; minimum: −1 at x=π
43. A linear function is added to a periodic sine function. The graph does not have an amplitude because as the linear function increases without bound the combined function h(x)=x+sin(x) will increase without bound as well. The graph is bounded between the graphs of y=x+1 and y=x−1 because sine oscillates between −1 and 1.
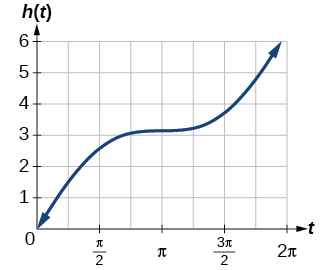
45. There is no amplitude because the function is not bounded.
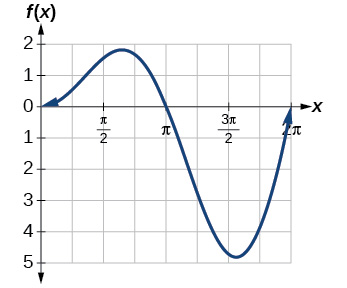
47. The graph is symmetric with respect to the y-axis and there is no amplitude because the function’s bounds decrease as |x| grows. There appears to be a horizontal asymptote at y=0 .
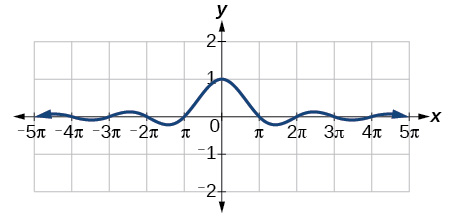
Section 3.2 - Graphs of the Other Trigonometric Functions
1. Since y=csc x is the reciprocal function of y=sin x, you can plot the reciprocal of the coordinates on the graph of y=sin x to obtain the y-coordinates of y=csc x. The x-intercepts of the graph y=sin x are the vertical asymptotes for the graph of y=csc x.
3. Answers will vary. Using the unit circle, one can show that tan(x+π)=tan x.
5. The period is the same: 2π.
7. IV
9. III
11. period: 8; horizontal shift: 1 unit to left
13. 1.5
15. 5
17. −cot(x)cos(x)−sin(x)
19.
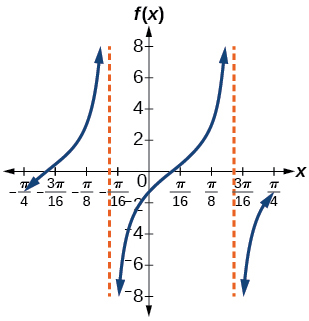
stretching factor: 2; period [latex]\frac{π}{4}[/latex]; asymptotes: [latex]x=\frac{1}{4}(\frac{π}{2}+πk)+8[/latex], where k is an integer
21.
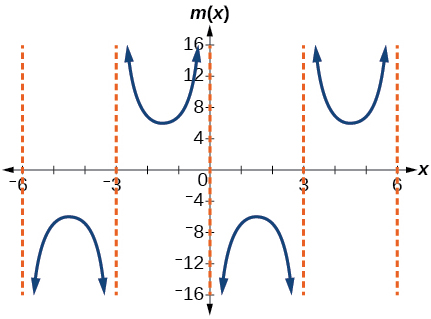
stretching factor: 6; period: 6; asymptotes x=3k, where k is an integer
23.
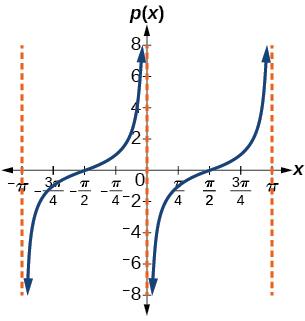
stretching factor: 1; period π; asymptotes: x=πk, where k is an integer
25.
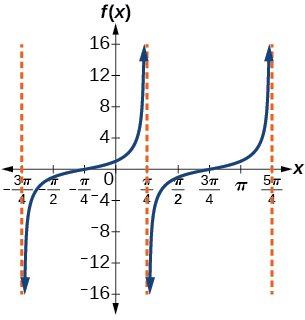
Stretching factor: 1; period π; asymptotes: [latex]x=\frac{π}{4}+πk[/latex], where k is an integer
27.
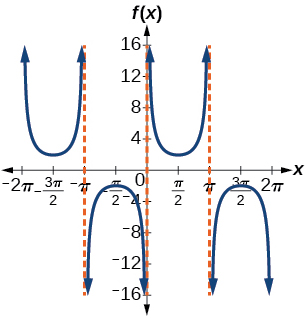
stretching factor: 2; period 2π; asymptotes: x=πk, where k is an integer
29.
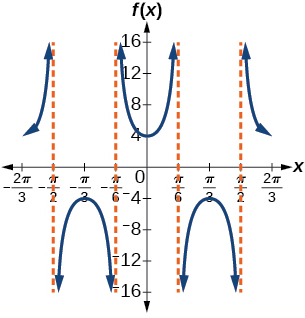
stretching factor: 4; period [latex]\frac{2π}{3}[/latex]; asymptotes: [latex]x=\frac{π}{6}k[/latex], where k is an odd integer
31.
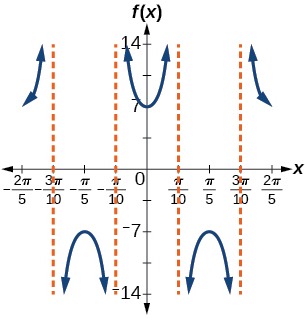
stretching factor: 7; period [latex]\frac{2π}{5}[/latex]; asymptotes: [latex]x=\frac{π}{10}k[/latex], where k is an odd integer
33.
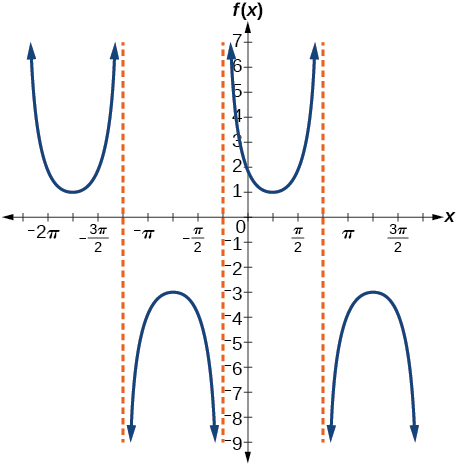
stretching factor: 2; period 2π; asymptotes: x=[latex]−\frac{π}{4}+πk[/latex], where k is an integer
35.
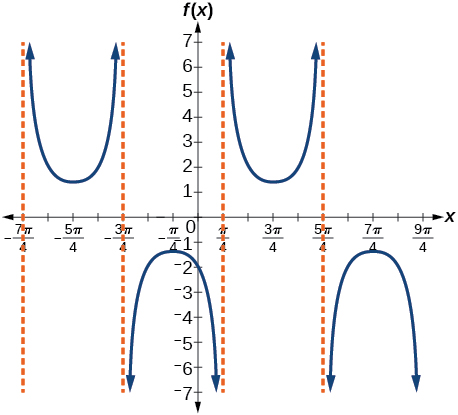
stretching factor [latex]\frac{7}{5}[/latex]; period: 2π; asymptotes: [latex]x=\frac{π}{4}+πk[/latex], where k is an integer
37. [latex]y=tan(3(x−\frac{π}{4}))+2[/latex]
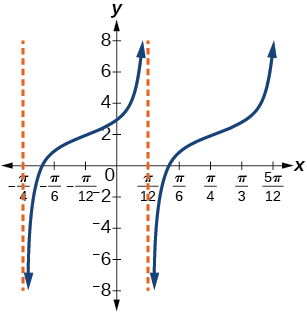
39. f(x)=css(2x)
41. f(x)=csc(4x)
43. f(x)=2csc(x)
45. [latex]f(x)=\frac{1}{2}tan(100πx)[/latex]
47.
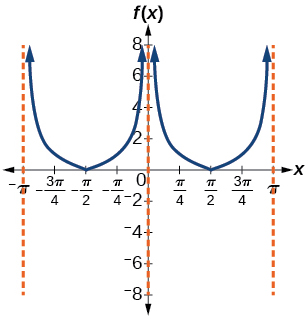
49.
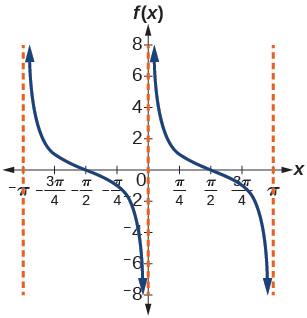
51.
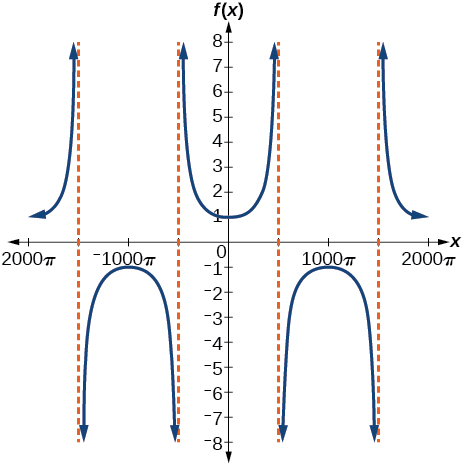
53.
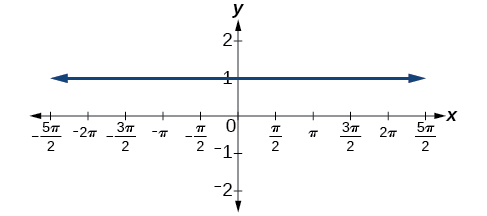
55.
ⓐ([latex]−\frac{π}{2}[/latex], [latex]\frac{π}{2}[/latex]);
ⓑ
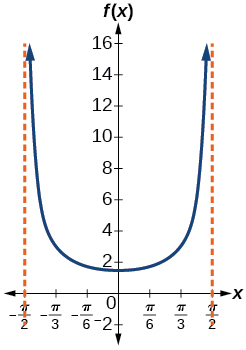
ⓒ [latex]x=−\frac{π}{2}[/latex] and [latex]x=\frac{π}{2}[/latex]; the distance grows without bound as |x| approaches [latex]\frac{π}{2}[/latex] —i.e., at right angles to the line representing due north, the boat would be so far away, the fisherman could not see it;
ⓓ3; when [latex]x=−\frac{π}{3}[/latex], the boat is 3 km away;
ⓔ 1.73; when [latex]x=\frac{π}{6}[/latex], the boat is about 1.73 km away;
ⓕ 1.5 km; when x=0
57.
ⓐ [latex]h(x)=2tan\frac{π}{120}x[/latex];
ⓑ
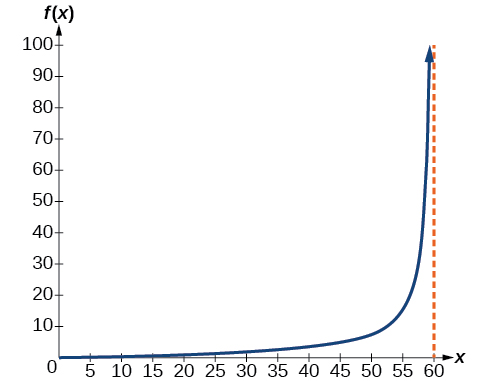
ⓒ h(0)=0: after 0 seconds, the rocket is 0 mi above the ground; h(30)=2: after 30 seconds, the rockets is 2 mi high;
ⓓAs x approaches 60 seconds, the values of h(x) grow increasingly large. The distance to the rocket is growing so large that the camera can no longer track it.
Section 3.3 - Inverse Functions
1. Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that y -values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no y -values repeat and the function is one-to-one.
3. Yes. For example, [latex]f(x)=\frac{1}{x}[/latex] is its own inverse.
5. Given a function y=f(x), solve for x in terms of y. Interchange the x and y. Solve the new equation for y. The expression for y is the inverse, [latex]y=f^{−1}(x)[/latex].
7. [latex]f^{−1}(x)=x−3[/latex]
9. [latex]f^{−1}(x)=2−x[/latex]
11. [latex]f^{−1}(x)=\frac{−2x}{x−1}[/latex]
13. domain of [latex]f(x): [−7,∞); f^{−1}(x)=\sqrt{x}−7[/latex]
15. domain of [latex]f(x): [0,∞); f^{−1}(x)=\sqrt{x+5}[/latex]
16.
- ⓐ f(g(x))=x and g(f(x))=x.
- ⓑ This tells us that f and g are inverse functions
17. f(g(x))=x, g(f(x))=x
19. one-to-one
21. one-to-one
23. not one-to-one
25. 3
27. 2
29.
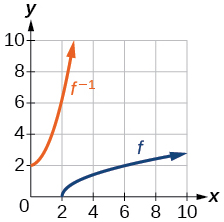
31. [2,10]
33. 6
35. −4
37. 0
39. 1
41.
| x |
1 |
4 |
7 |
12 |
16 |
| [latex]f^{−1}(x)[/latex] |
3 |
6 |
9 |
13 |
14 |
43. [latex]f^{−1}(x)=(1+x)^{\frac{1}{3}}[/latex]
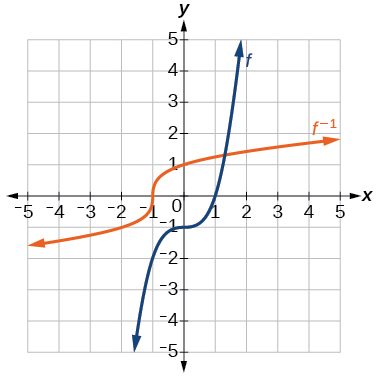
45. [latex]f^{−1}(x)=\frac{5}{9}(x−32)[/latex]. Given the Fahrenheit temperature, x, this formula allows you to calculate the Celsius temperature.
47. [latex]t(d)=\frac{d}{50}, t(180)=\frac{180}{50}[/latex]. The time for the car to travel 180 miles is 3.6 hours.
Section 3.4 - Inverse Trigonometric Functions
1. The function y=sin(x) is one-to-one on [[latex]−\frac{π}{2}[/latex][latex],\frac{π}{2}[/latex]]; thus, this interval is the range of the inverse function of [latex]y=sin(x), f(x)=sin^{−1}x[/latex]. The function y=cos(x) is one-to-one on [0,π]; thus, this interval is the range of the inverse function of [latex]y=cos(x), f(x)=cos^{−1}x[/latex].
3. [latex]\frac{π}{6}[/latex] is the radian measure of an angle between [latex]−\frac{π}{2}[/latex] and [latex]\frac{π}{2}[/latex] whose sine is 0.5.
5. In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval [[latex]−\frac{π}{2}[/latex],[latex]\frac{π}{2}[/latex]] so that it is one-to-one and possesses an inverse.
7. True . The angle, [latex]θ_1[/latex] that equals arccos(−x) , x>0 , will be a second quadrant angle with reference angle, [latex]θ_2[/latex] , where [latex]θ_2[/latex] equals arccosx , x>0 . Since [latex]θ2[/latex] is the reference angle for [latex]θ_1[/latex] , [latex]θ_2=π−θ_1[/latex] and arccos(−x) = π−arccosx
9. [latex]−\frac{π}{6}[/latex]
11. [latex]\frac{3π}{4}[/latex]
13. [latex]−\frac{π}{3}[/latex]
15. [latex]\frac{π}{3}[/latex]
17. 1.98
19. 0.93
21. 1.41
23. 0.56 radians
25. 0
27. 0.71
29. -0.71
31. [latex]−\frac{π}{4}[/latex]
33. 0.8
35. 513
37. [latex]\frac{x−1}{\sqrt{−x^2+2x}}[/latex]
39. [latex]\frac{\sqrt{x^2−1}}{x}[/latex]
41. [latex]\frac{x+0.5}{\sqrt{−x^2−x+\frac{3}{4}}}[/latex]
43. [latex]\frac{\sqrt{2x+1}}{x+1}[/latex]
45. [latex]\frac{\sqrt{2x+1}}{x}[/latex]
47. [latex]t[/latex]
49.
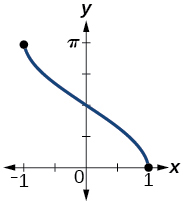
domain [−1,1]; range [0,π]
51. approximately x=0.00
53. 0.395 radians
55. 1.11 radians
57. 1.25 radians
59. 0.405 radians
61. No. The angle the ladder makes with the horizontal is 60 degrees.

