At the end of 2019, the first cases of the coronavirus disease (COVID-19) began to surface. By the beginning of 2020, not only were cities like San Antonio rapidly starting to record larger numbers of new cases for the virus but the World Health Organization declared the spread of COVID-19 to be a global pandemic.

In the face of these substantial global challenges, the utilization of mathematical models becomes even more crucial in understanding and predicting the various dynamics of the pandemic. The progression of the outbreak exhibits a pattern that aligns itself well with the mathematical applications of both exponential and logarithmic functions. Exponential functions capture the growth rate of infections, which offer an insight into the rapid spread that characterizes the early stages of the virus. On the other hand, logarithmic functions can highlight the decay rate of infections as numerous interventions, vaccinations, and social policies begin to take effect.

An example of the power of mathematics to establish infectious disease models comes from our own department. Between 2020 and 2022, UTSA Mathematics Department Chair Dr. Juan B. Gutiérrez conducted extensive research on the community transmission of COVID-19. A component of this research was attempting to develop different mathematical models to graphically and functionally represent the spread of the virus. As with most mathematical models, there are limitations and challenges associated with modeling these trends, and there is a need for constant refinement in response to the evolving circumstances. However, through the use of deliberate parameters, Dr. Gutiérrez successfully established an exponential function that modeled the growth rate of COVID-19 cases at the beginning of the pandemic.

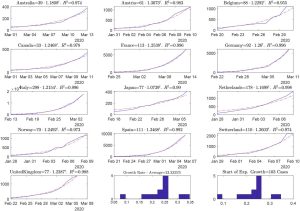
As revealed, the fundamental concepts of mathematics are used every day to explore and connect these ideas to the experiences of our world, and COVID-19 is no exception. By establishing exponential and logarithmic functions based on real data, we are able to create models which predict future trends, ultimately assisting policymakers, healthcare professionals, and the public in making informed decisions.

♠     ♣     ♥     ♦

In Chapter 6 we will learn important features of and details about exponential functions. An exponential function is a growth or decay function that grows or shrinks at a constant percentage or by a constant factor. In this module, you will explore exponential functions in terms of growth or decay and learn to formulate an equation for exponential functions. You will also have the opportunity to recognize graphs of exponential functions, transformations of these graphs, and state features such as domain and range, asymptotes, and intercepts. You will also consider these functions in real-world contexts.

Chapter 6 also introduces us to logarithmic functions. A logarithmic function is the inverse of an exponential function. In this module, you will solve logarithms without a calculator and explore the properties of logarithmic graphs such as domain, range, asymptotes, and intercepts. You will also have the opportunity to formulate exponential and logarithmic expressions and equations using their properties, convert equations between logarithmic and exponential form, identify graphs of translated logarithmic and exponential equations, and solve equations that are exponential and logarithmic in form.

These are just a few of the important concepts and ideas included in Chapter 6. A complete list of the Key Takeaways from the chapter is organized in the table below: