You head to the UC to grab a Mountain Dew from a vending machine. As you swipe your UTSA ID card and push B9, you wonder how the machine knows that pressing B9 means you want a Mountain Dew? Taking a sip of your sugary and refreshing beverage, you contemplate the dwindling Rowdy Dollars in your account. How does the vending machine deduct money from your account and not your roommates’ when you pay by swipe using your UTSA ID card? The answer to these questions is functions, of course! A helpful image to make sense of these relationships is a function machine:

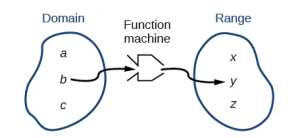
In the case of the vending machine, B9 is an element in the Domain of the function that corresponds to a single item in the Range (the can of Mountain Dew). Is B9 the only element in the Domain that maps to the can of Mountain Dew? If not, this is not a one-to-one function. On the other hand, your UTSA ID card is a unique form of identification that is associated only with you (and your financial account!). A swipe of your card maps to only your account, and your financial account corresponds with only your personal identification! This is a one-to-one function.

♠     ♣     ♥     ♦

In this chapter, we will explore these kinds of relationships and their properties. We will start by describing the difference between functions and relations so you can answer the question what is so special about a function? We will differentiate between the many different forms of a function in both abstract and real-world models. Finally, we’ll discuss domain and range, and what it means for a function to be one-to-one (what we like to call, the ultimate function).

These are just a few of the important concepts and ideas included in Chapter 1. A complete list of the Key Takeaways from the chapter is organized in the table below: