Chapter 6 – Exponential and Logarithmic Functions
"Try It" Exercises
Section 6.1 - Exponential Functions
1. [latex]g(x)=0.875^x[/latex] and [latex]j(x)=1095.6^{−2x}[/latex] represent exponential functions.
2. [latex]5.5556[/latex]
3. About [latex]1.548[/latex] billion people; by the year 2031, India’s population will exceed China’s by about 0.001 billion, or 1 million people.
4. [latex](0,129)[/latex] and [latex](2,236)[/latex]; [latex]N(t)=129(1.3526)^t[/latex]
5. [latex]f(x)=2(1.5)^x[/latex]
6. [latex]f(x)=\sqrt{2}(\sqrt{2})^x[/latex]. Answers may vary due to round-off error. The answer should be very close to [latex](1.4142)(1.4142)^x[/latex].
7. about $3,644,675.88
8. $13,693
9. $3,659,823.44
10. 3.77E-26 (This is calculator notation for the number written as [latex]3.77×10^{−26}[/latex] in scientific notation. While the output of an exponential function is never zero, this number is so close to zero that for all practical purposes we can accept zero as the answer.)
11. The domain is [latex](−∞,∞)[/latex]; the range is [latex](0,∞)[/latex]; the horizontal asymptote is [latex]y=0[/latex].
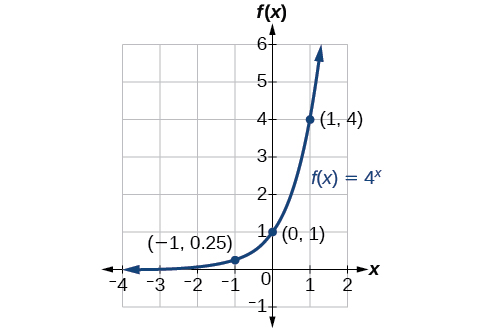
12. [latex]f(x)=−\frac{1}{3}e^x−2[/latex]; the domain is [latex](−∞,∞)[/latex]; the range is [latex](−∞,−2)[/latex]; the horizontal asymptote is [latex]y=−2[/latex].
Section 6.2 - Logarithmic Functions
1. ⓐ [latex]log_{10}(1,000,000)=6[/latex] is equivalent to [latex]10^6=1,000,000[/latex]
ⓑ [latex]log_5(25)=2[/latex] is equivalent to [latex]5^2=25[/latex]
2. ⓐ [latex]3^2=9[/latex] is equivalent to [latex]log_3(9)=2[/latex]
ⓑ [latex]5^3=125[/latex] is equivalent to [latex]log_5(125)=3[/latex]
ⓒ [latex]2^{−1}=\frac{1}{2}[/latex] is equivalent to [latex]log_2(\frac{1}{2})=−1[/latex]
3. [latex]log_{121}(11)=\frac{1}{2}[/latex] (recalling that [latex]\sqrt{121}=(121)^{\frac{1}{2}}=11[/latex])
4. [latex]log_2(\frac{1}{32})=−5[/latex]
5. [latex]log(1,000,000)=6[/latex]
6. [latex](2,∞)[/latex]
7. [latex](5,∞)[/latex]
8.
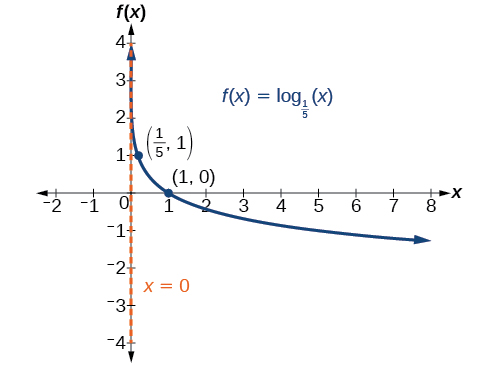
The domain is [latex](0,∞)[/latex], the range is [latex](−∞,∞)[/latex], and the vertical asymptote is [latex]x=0[/latex].
9. [latex]x=1[/latex]
10. [latex]f(x)=2ln(x+3)−1[/latex]
Section 6.3 - Logarithmic Properties
1. [latex]log_b(2)+log_b(2)+log_b(2)+log_b(k)=3log_b(2)+log_b(k)[/latex]
2. [latex]log_3(x+3)−log_3(x−1)−log_3(x−2)[/latex]
3. [latex]2ln(x)[/latex]
4. [latex]−2ln(x)[/latex]
5. [latex]log_3(16)[/latex]
6. [latex]2log(x)+3log(y)−4log(z)[/latex]
7. [latex]\frac{2}{3}ln(x)[/latex]
8. [latex]\frac{1}{2}ln(x−1)+ln(2x+1)−ln(x+3)−ln(x−3)[/latex]
9. [latex]log(\frac{3⋅5}{4⋅6})[/latex]; can also be written [latex]log(\frac{5}{8})[/latex]
by reducing the fraction to lowest terms.
10. [latex]log(\frac{5(x−1)^3\sqrt{x}}{(7x−1)})[/latex]
11. [latex]log(\frac{x^{12}(x+5)^4}{(2x+3)^4})[/latex]; this answer could also be written [latex]log(\frac{x^3(x+5)}{(2x+3)})^4[/latex].
12. The pH increases by about 0.301.
13. [latex]\frac{ln(8)}{ln(0.5)}[/latex]
Section 6.4 - Exponential and Logarithmic Equations
1. [latex]x=−2[/latex]
2. [latex]x=−1[/latex]
3. [latex]x=\frac{1}{2}[/latex]
4. The equation has no solution.
5. [latex]x=\frac{ln(3)}{ln(\frac{2}{3})}[/latex]
6. [latex]t=2ln(\frac{11}{3})[/latex] or [latex]ln(\frac{11}{3})^2[/latex]
7. [latex]t=ln(\frac{1}{\sqrt{2}})=−\frac{1}{2}ln(2)[/latex]
8. [latex]x=ln(2)[/latex]
9. [latex]x=e^4[/latex]
10. [latex]x=e^5−1[/latex]
11. [latex]x≈9.97[/latex]
12. [latex]x=1[/latex] or [latex]x=−1[/latex]
13. [latex]t=703,800,000×\frac{ln(0.8)}{ln(0.5)}[/latex] years [latex]≈ 226,572,993[/latex] years.
Section Exercises
Section 6.1 - Exponential Functions
1. Linear functions have a constant rate of change. Exponential functions increase based on a percent of the original.
3. An asymptote is a line that the graph of a function approaches, as [latex]x[/latex] either increases or decreases without bound. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.
5. exponential; the population decreases by a proportional rate. .
7. The forest represented by the function [latex]B(t)=82(1.029)^t[/latex].
9. After [latex]t=20[/latex] years, forest A will have [latex]43[/latex] more trees than forest B.
11. exponential growth; The growth factor, [latex]1.06[/latex], is greater than [latex]1[/latex].
13. [latex]f(x)=2000(0.1)^x[/latex]
15. Linear
17. $15,281.04
19. 10 years
21. continuous decay; the growth rate is less than [latex]0[/latex].
23. [latex]g(x)=4(3)^{−x}[/latex]; y-intercept: [latex](0,4)[/latex]; Domain: all real numbers; Range: all real numbers greater than [latex]0[/latex].
25. y-intercept: [latex](0,−2)[/latex]

27. B
29. A
31. E
33. D
35. As [latex]x→∞[/latex], [latex]f(x)→−∞[/latex];
As [latex]x→−∞[/latex], [latex]f(x)→−1[/latex]
37. As [latex]x→∞[/latex], [latex]f(x)→2[/latex];
As [latex]x→−∞[/latex], [latex]f(x)→∞[/latex]
39. Horizontal asymptote: [latex]h(x)=3[/latex]; Domain: all real numbers; Range: all real numbers strictly greater than [latex]3[/latex].
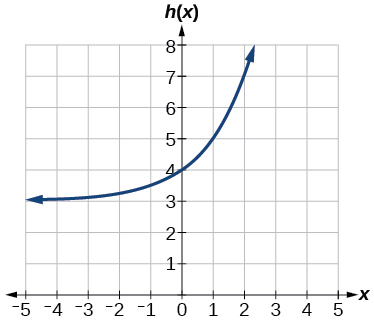
41. [latex]f(x)=4^x+4[/latex]
43. [latex]f(x)=-4^x[/latex]
45. [latex]f(x)=-2^{x+2}+1[/latex]
47. [latex]y=−2(3)^x+7[/latex]
49. [latex]f(−1)=−4[/latex]
51. [latex]f(−1)≈−0.2707[/latex]
53. [latex]h(−7)=−58[/latex]
55. Let [latex]f[/latex] be the exponential decay function [latex]f(x)=a⋅(\frac{1}{b})^x[/latex] such that [latex]b>1[/latex]. Then for some number [latex]n>0[/latex], [latex]f(x)=a⋅(\frac{1}{b})^x=a(b^{−1})^x=a((e^n)^{−1})^x=a(e^{−n})^x=a(e)^{−nx}[/latex].
57. The graphs of [latex]g(x)[/latex] and [latex]h(x)[/latex] are the same and are a horizontal shift to the right of the graph of [latex]f(x)[/latex]; For any real number n, real number [latex]b>0[/latex], and function [latex]f(x)=b^x[/latex], the graph of [latex](\frac{1}{b^n})b^x[/latex] is the horizontal shift [latex]f(x−n)[/latex].
59. 47,622 fox
61. 1.39%; $155,368.09
Section 6.2 - Logarithmic Functions
1. A logarithm is an exponent. Specifically, it is the exponent to which a base [latex]b[/latex] is raised to produce a given value. In the expressions given, the base [latex]b[/latex] has the same value. The exponent, [latex]y[/latex], in the expression [latex]b^y[/latex] can also be written as the logarithm, [latex]log_bx[/latex], and the value of [latex]x[/latex] is the result of raising [latex]b[/latex] to the power of [latex]y[/latex].
3. Since the equation of a logarithm is equivalent to an exponential equation, the logarithm can be converted to the exponential equation [latex]b^y=x[/latex], and then properties of exponents can be applied to solve for [latex]x[/latex].
5. Since the functions are inverses, their graphs are mirror images about the line [latex]y=x[/latex]. So for every point [latex](a,b)[/latex] on the graph of a logarithmic function, there is a corresponding point [latex](b,a)[/latex] on the graph of its inverse exponential function.
7. Shifting the function right or left and reflecting the function about the y-axis will affect its domain.
9. [latex]a^c=b[/latex]
11. [latex]15^b=a[/latex]
13. [latex]e^n=w[/latex]
15. [latex]log_{19}(y)=x[/latex]
17. [latex]ln(h)=k[/latex]
19. [latex]x=e^2[/latex]
21. 32
23. 1.06
25. Domain: [latex](−\frac{17}{4},∞)[/latex]; Range: [latex](−∞,∞)[/latex]
27. Domain: [latex](−\frac{1}{3},∞)[/latex]; Vertical asymptote: [latex]x=−\frac{1}{3}[/latex]
29. Domain: [latex](1,∞)[/latex]; Range: [latex](−∞,∞)[/latex]; Vertical asymptote: [latex]x=1[/latex]; x-intercept: [latex](\frac{5}{4},0)[/latex]; y-intercept: DNE
31. Domain: [latex](0,∞)[/latex]; Range: [latex](−∞,∞)[/latex]; Vertical asymptote: [latex]x=0[/latex]; x-intercept: [latex](e^3,0)[/latex]; y-intercept: DNE
33. Domain: [latex](\frac{3}{7},∞)[/latex]; Vertical asymptote: [latex]x=\frac{3}{7}[/latex]; End behavior: as
35. Domain: [latex](\frac{4}{3},∞)[/latex]; Vertical asymptote: [latex]x=\frac{4}{3}[/latex];
End behavior: as [latex]x→(\frac{4}{3})+[/latex], [latex]f(x)→∞[/latex] and as [latex]x→∞[/latex], [latex]f(x)→-∞[/latex]
37. B
39. C
41. [latex]f(x)=log_2(−(x−1))[/latex]
43. [latex]\frac{1}{2}[/latex]
45. 4
47. −12
49. 0
51. No, the function has no defined value for [latex]x=0[/latex]. To verify, suppose [latex]x=0[/latex] is in the domain of the function [latex]f(x)=log(x)[/latex]. Then there is some number
53. Yes. Suppose there exists a real number [latex]x[/latex] such that [latex]ln(x)=2[/latex]. Rewriting as an exponential equation gives [latex]x=e^2[/latex], which is a real number. To verify, let [latex]x=e^2[/latex]. Then, by definition, [latex]ln(x)=ln(e^2)=2[/latex].
55. Recall that the argument of a logarithmic function must be positive, so we determine where [latex]\frac{x+2}{x−4}>0[/latex]. From the graph of the function [latex]f(x)=\frac{x+2}{x−4}[/latex], note that the graph lies above the x-axis on the interval [latex](−∞,−2)[/latex] and again to the right of the vertical asymptote, that is [latex](4,∞)[/latex]. Therefore, the domain is [latex](−∞,−2)∪(4,∞)[/latex].
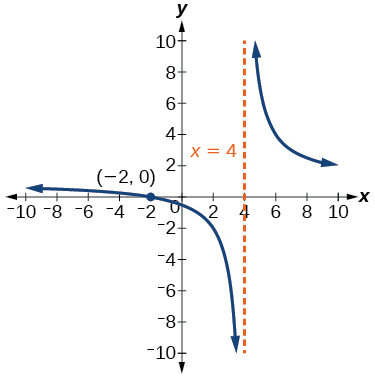
Section 6.3 - Logarithmic Properties
1. Any root expression can be rewritten as an expression with a rational exponent so that the power rule can be applied, making the logarithm easier to calculate. Thus, [latex]log_b(x^{\frac{1}{n}})=\frac{1}{n}log_b(x).[/latex]
3. [latex]log_b(2)+log_b(7)+log_b(x)+log_b(y)[/latex]
5. [latex]log_b(13)−log_b(17)[/latex]
7. [latex]−kln(4)[/latex]
9. [latex]ln(7xy)[/latex]
11. [latex]log_b(4)[/latex]
13. [latex]log_b(7)[/latex]
15. [latex]15log(x)+13log(y)−19log(z)[/latex]
17. [latex]\frac{3}{2}log(x)−2log(y)[/latex]
19. [latex]\frac{8}{3}log(x)+\frac{14}{3}log(y)[/latex]
21. [latex]ln(2x^7)[/latex]
23. [latex]log(\frac{xz^3}{\sqrt{y}})[/latex]
25. [latex]log_7(15)=\frac{ln(15)}{ln(7)}[/latex]
27. [latex]log_{11}(5)=\frac{log_5(5)}{log_5(11)}=\frac{1}{b}[/latex]
29. [latex]log_11(\frac{6}{11})=\frac{log_5(\frac{6}{11})}{log_5(11)}=\frac{log_5(6)−log_5(11)}{log_5(11)}=\frac{a−b}{b}=\frac{a}{b}−1[/latex]
31. [latex]3[/latex]
33. [latex]2.81359[/latex]
35. [latex]0.93913[/latex]
37. [latex]−2.23266[/latex]
39. [latex]x=4[/latex]; By the quotient rule: [latex]log_6(x+2)−log_6(x−3)=log_6(\frac{x+2}{x−3})=1[/latex]. Rewriting as an exponential equation and solving for [latex]x[/latex]:
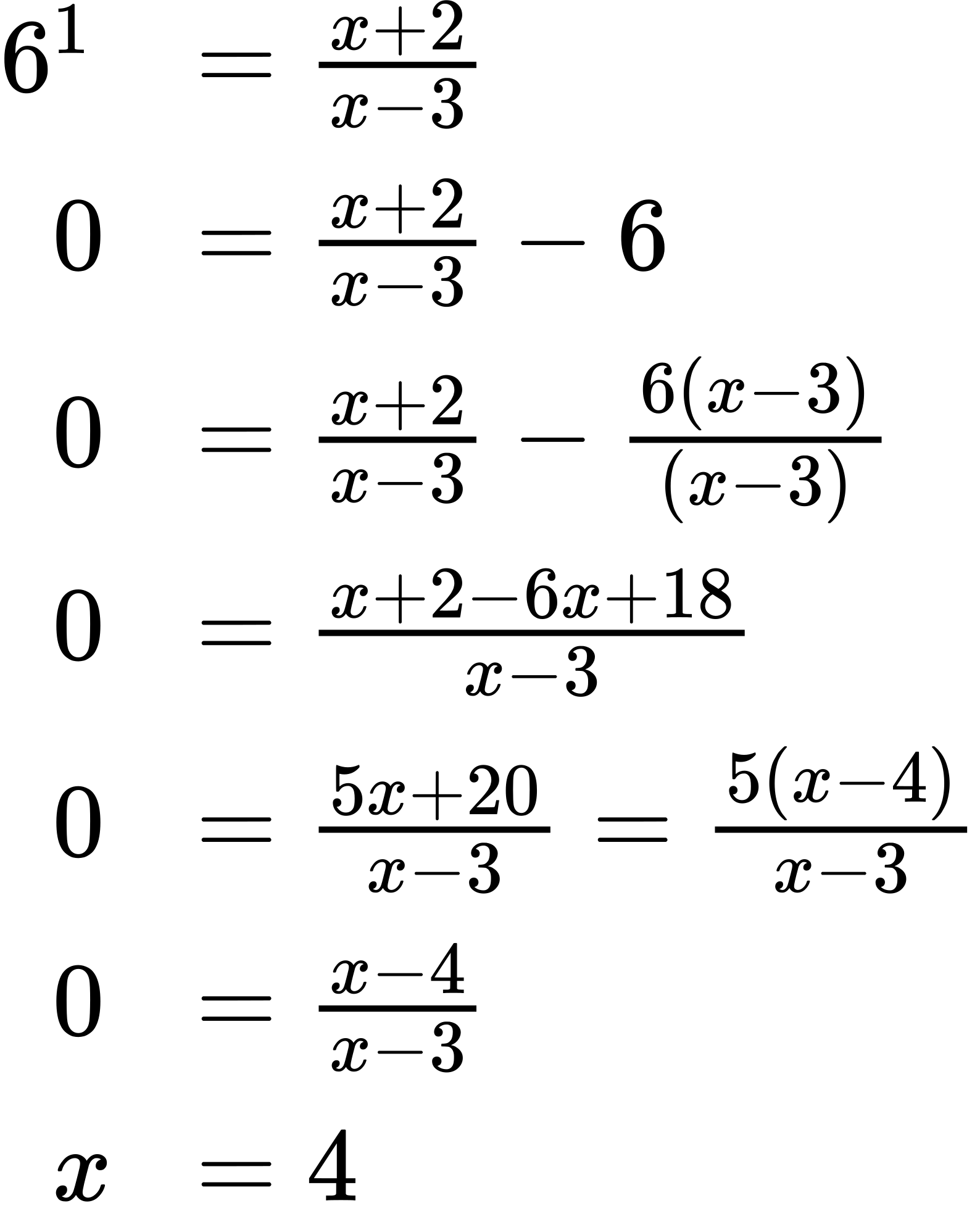
Checking, we find that [latex]log_6(4+2)−log_6(4−3)=log_6(6)−log_6(1)[/latex] is defined, so [latex]x=4[/latex].
41. Let [latex]b[/latex] and [latex]n[/latex] be positive integers greater than [latex]1[/latex]. Then, by the change-of-base formula, [latex]log_b(n)=\frac{log_n(n)}{log_n(b)}=\frac{1}{log_n(b)}[/latex].
Section 6.4 - Exponential and Logarithmic Equations
1. Determine first if the equation can be rewritten so that each side uses the same base. If so, the exponents can be set equal to each other. If the equation cannot be rewritten so that each side uses the same base, then apply the logarithm to each side and use properties of logarithms to solve.
3. The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.
5. [latex]x=−\frac{1}{3}[/latex]
7. [latex]n=−1[/latex]
9. [latex]b=\frac{6}{5}[/latex]
11. [latex]x=10[/latex]
13. No solution
15. [latex]p=log(\frac{17}{8})−7[/latex]
17. [latex]k=−\frac{ln(38)}{3}[/latex]
19. [latex]x=\frac{ln(\frac{38}{3})−8}{9}[/latex]
21. [latex]x=ln(12)[/latex]
23. [latex]x=\frac{ln(\frac{3}{5})−3}{8}[/latex]
25. No solution
27. [latex]x=ln(3)[/latex]
29. [latex]10^{−2}=\frac{1}{100}[/latex]
31. [latex]n=49[/latex]
33. [latex]k=\frac{1}{36}[/latex]
35. [latex]x=\frac{9−e}{8}[/latex]
37. [latex]n=1[/latex]
39. No solution
41. No solution
43. [latex]x=±\frac{10}{3}[/latex]
45. [latex]x=10[/latex]
47. [latex]x=0[/latex]
49. [latex]x=\frac{3}{4}[/latex]
51. [latex]x=9[/latex]
53. [latex]x=\frac{e^2}{3}≈2.5[/latex]
55. [latex]x=−5[/latex]
57. [latex]x=\frac{e+10}{4}≈3.2[/latex]
59. No solution
61. [latex]x=\frac{11}{5}≈2.2[/latex]
63. [latex]x=\frac{101}{11}≈9.2[/latex]

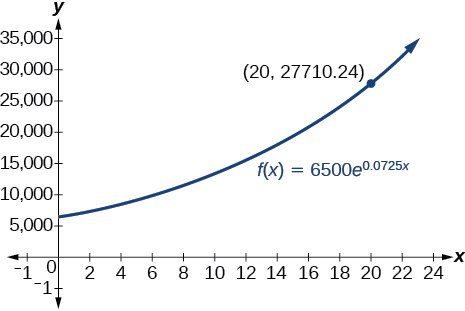
65. about $[latex]27,710.24[/latex]
67. about 5 years
69. [latex]t=ln((\frac{y}{A})^{\frac{1}{k}})[/latex]
71. [latex]t=ln((\frac{T−T_s}{T_0−T_s})^{−\frac{1}{k}})[/latex]

