Chapter 4 – Trigonometric Identities and Equations
"Try It" Exercises
Section 4.1 - Solving Trigonometric Equations with Identities
1.
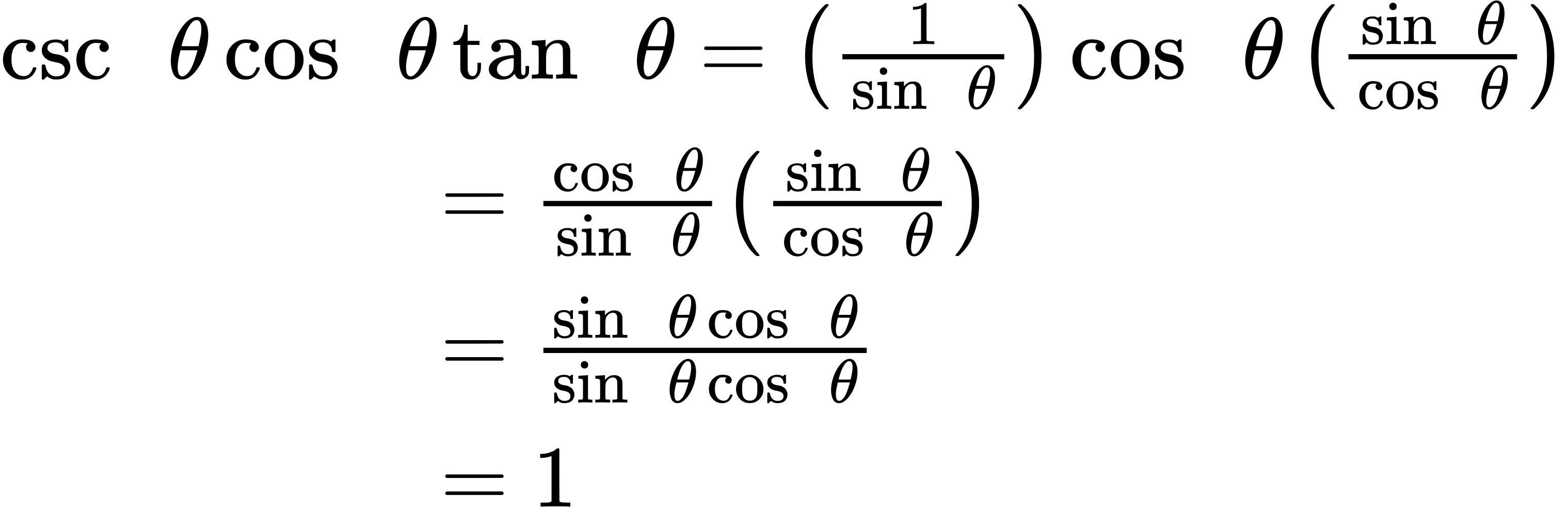
2.
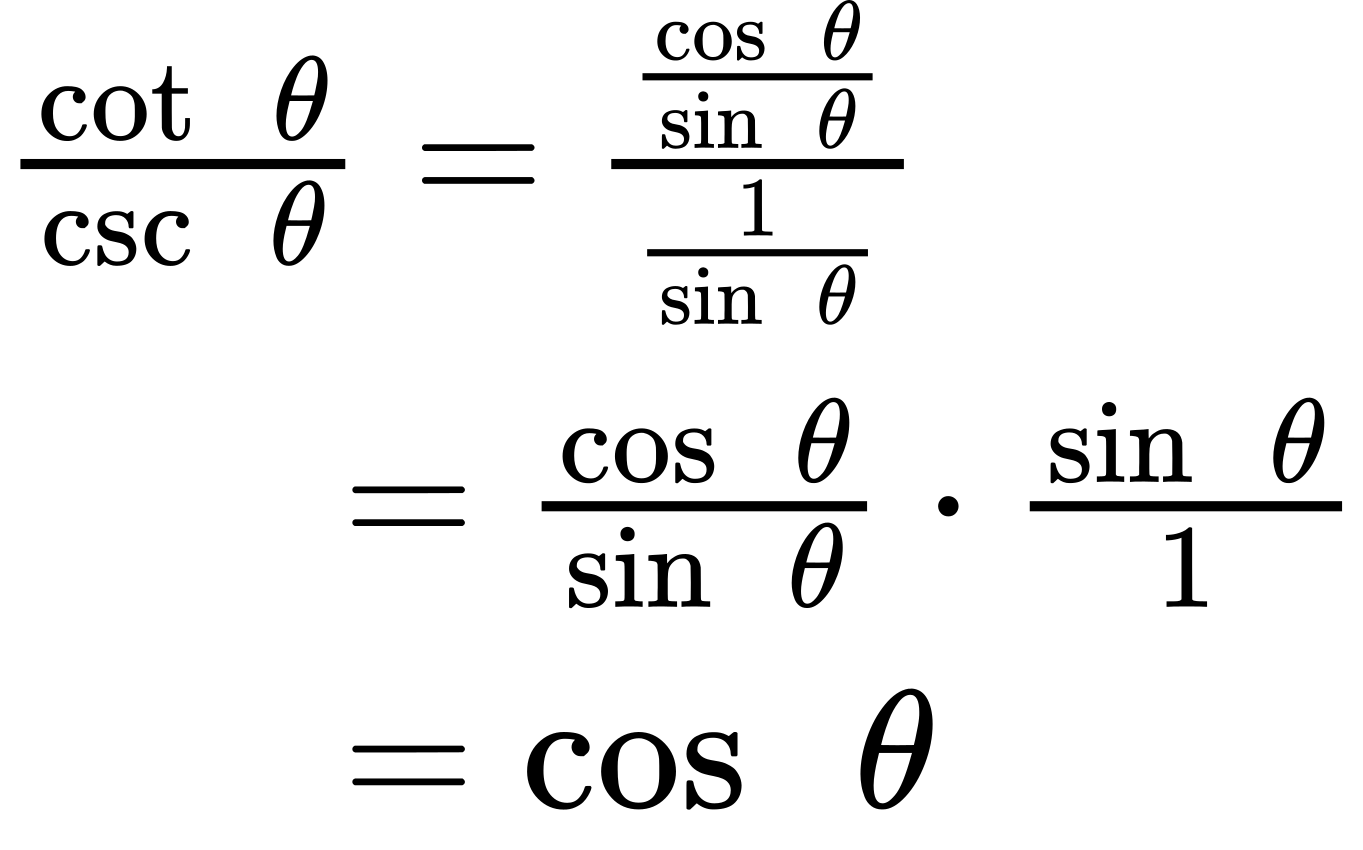
3.
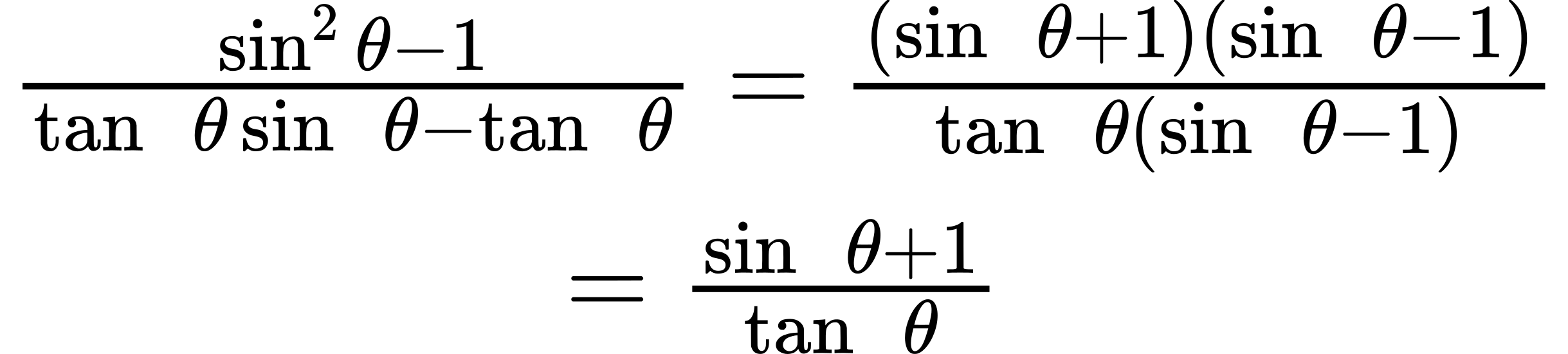
4. This is a difference of squares formula: 25 − 9 [latex]sin^2[/latex] [latex]θ[/latex] = (5 − 3 [latex]sin[/latex] [latex]θ[/latex])(5 + 3 [latex]sin[/latex] [latex]θ[/latex]).
5.
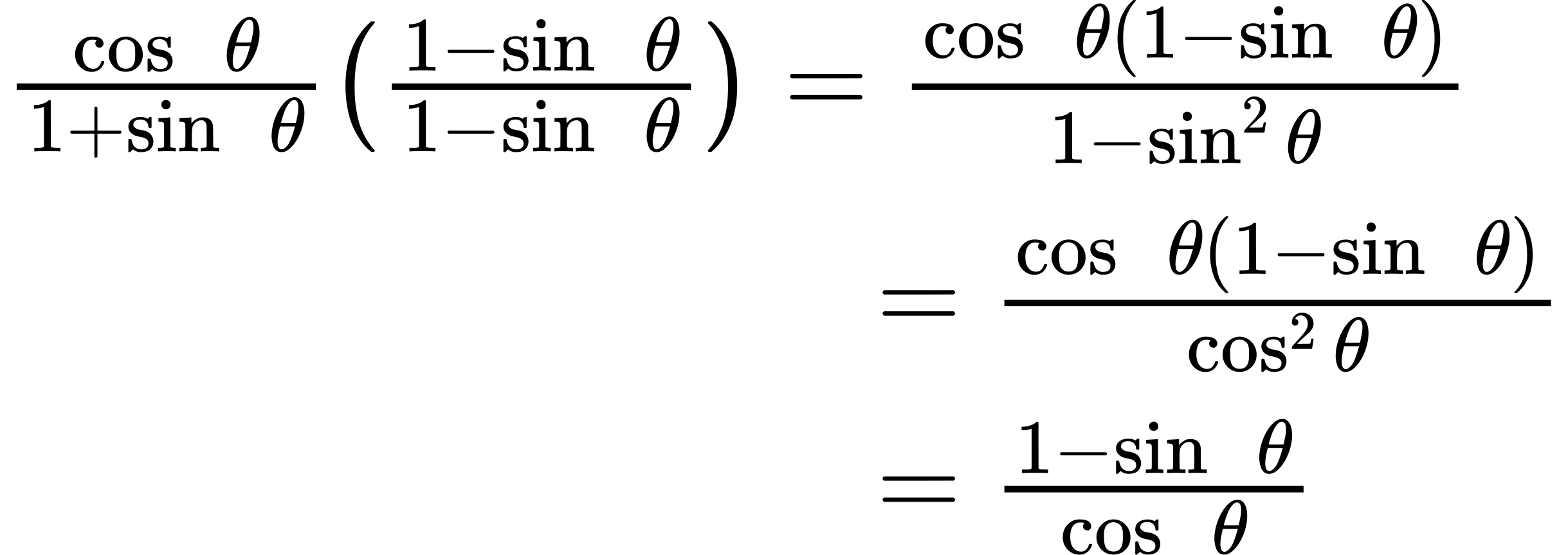
Section 4.2 - Sum and Difference Identities
1. [latex]\frac{\sqrt{2} + \sqrt{6}}{4}[/latex]
2. [latex]\frac{\sqrt{2} − \sqrt{6}}{4}[/latex]
3. [latex]\frac{1 − \sqrt{3}}{1 + \sqrt{3}}[/latex]
4. [latex]cos[/latex] ([latex]\frac{5π}{14}[/latex])
5.
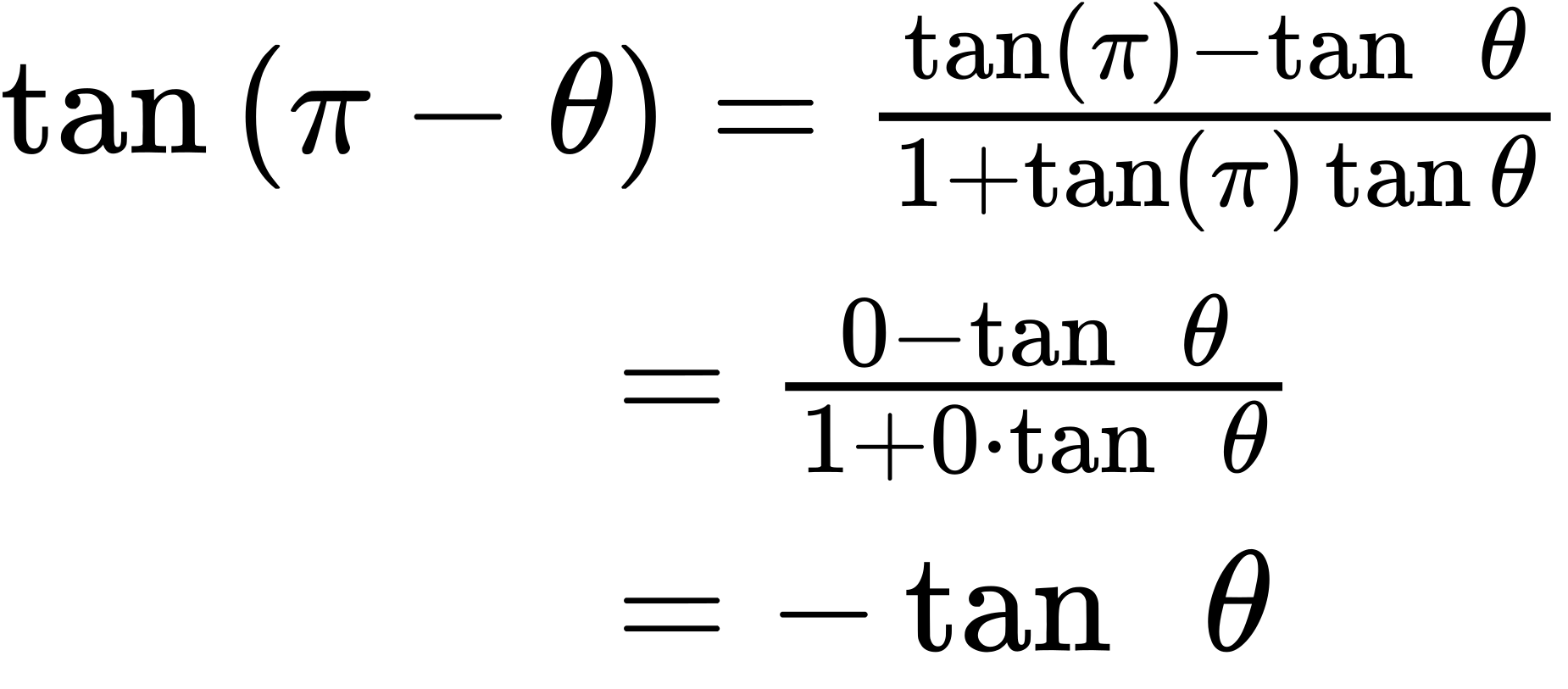
Section 4.3 - Double-Angle, Half-Angle, and Reduction Formulas
1. [latex]cos[/latex] ([latex]2α[/latex]) = [latex]\frac{7}{32}[/latex]
2. [latex]cos^4[/latex] [latex]θ[/latex] − [latex]sin^4[/latex] [latex]θ[/latex] = ([latex]cos^2[/latex] [latex]θ[/latex] + [latex]sin^2[/latex] [latex]θ[/latex])([latex]cos^2[/latex] [latex]θ[/latex] − [latex]sin^2[/latex] [latex]θ[/latex]) = [latex]cos[/latex] ([latex]2θ[/latex])
3. [latex]cos[/latex] ([latex]2θ[/latex]) [latex]cos[/latex] [latex]θ[/latex] = ([latex]cos^2[/latex] [latex]θ[/latex] − [latex]sin^2[/latex] [latex]θ[/latex]) [latex]cos[/latex] [latex]θ[/latex] = [latex]cos^3[/latex] [latex]θ[/latex] − [latex]cos[/latex] [latex]θ[/latex] [latex]sin^2[/latex] [latex]θ[/latex]
4.

5. [latex]{−2}{\sqrt{5}}[/latex]
Section 4.4 - Sum-to-Product and Product-to-Sum Formulas
1. [latex]\frac{1}{2}[/latex] ([latex]cos[/latex] [latex]6θ[/latex] + [latex]cos[/latex] [latex]2θ[/latex])
2. [latex]\frac{1}{2}[/latex] ([latex]sin[/latex] [latex]2x[/latex] + [latex]sin[/latex] [latex]2y[/latex])
3. [latex]\frac{−2 − \sqrt{3}}{4}[/latex]
4. 2 [latex]sin[/latex] ([latex]2θ[/latex]) [latex]cos[/latex] ([latex]θ[/latex])
5.
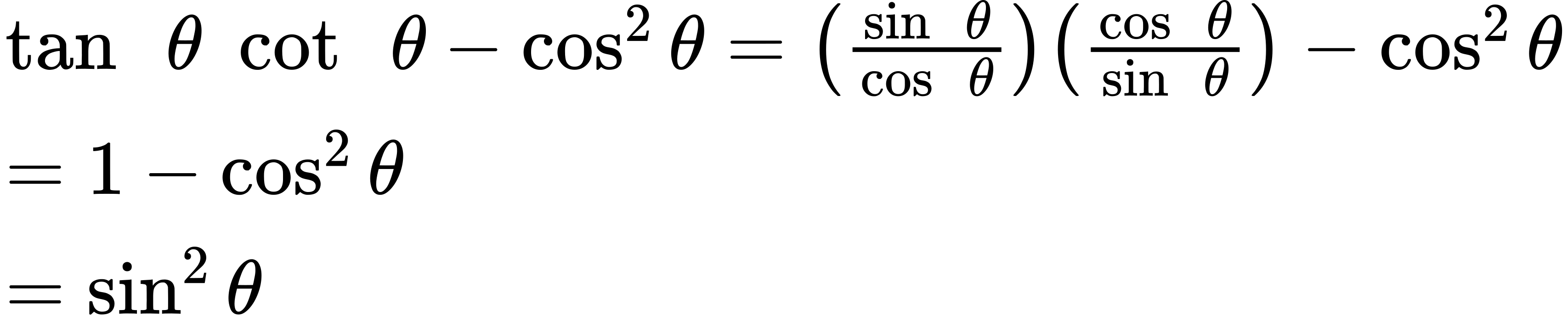
Section 4.5 - Solving Trigonometric Equations
1. [latex]x[/latex] = [latex]\frac{7π}{6}[/latex], [latex]\frac{11π}{6}[/latex]
2. [latex]\frac{π}{3}[/latex] ± [latex]πk[/latex]
3. [latex]cos[/latex] [latex]θ[/latex] = −1, [latex]θ[/latex] = [latex]π[/latex]
4. [latex]\frac{π}{2}[/latex], [latex]\frac{2π}{3}[/latex], [latex]\frac{4π}{3}[/latex], [latex]\frac{3π}{2}[/latex]
Section Exercises
Section 4.1 - Solving Trigonometric Equations with Identities
1. All three functions, [latex]F[/latex], [latex]G[/latex], and [latex]H[/latex], are even.
This is because [latex]F[/latex](−[latex]x[/latex]) = [latex]sin[/latex] (−[latex]x[/latex]) [latex]sin[/latex] (−[latex]x[/latex]) = (−[latex]sin[/latex] [latex]x[/latex])(−[latex]sin[/latex] [latex]x[/latex]) = [latex]sin^2[/latex] [latex]x[/latex] = [latex]F[/latex]([latex]x[/latex]), [latex]G[/latex](−[latex]x[/latex]) = [latex]cos[/latex] (−[latex]x[/latex]) [latex]cos[/latex] (−[latex]x[/latex]) = ([latex]cos[/latex] [latex]x[/latex])([latex]cos[/latex] [latex]x[/latex]) = [latex]cos^2[/latex] [latex]x[/latex] = [latex]G[/latex]([latex]x[/latex]) and [latex]H[/latex](−[latex]x[/latex]) = [latex]tan[/latex] (−[latex]x[/latex]) [latex]tan[/latex] (−[latex]x[/latex]) = (−[latex]tan[/latex] [latex]x[/latex])(−[latex]tan[/latex] [latex]x[/latex]) = [latex]tan^2[/latex] [latex]x[/latex] = [latex]H[/latex]([latex]x[/latex]).
3. When [latex]cos[/latex] [latex]t[/latex] = 0, then [latex]sec[/latex] [latex]t[/latex] = [latex]\frac{1}{0}[/latex], which is undefined.
5. [latex]sin[/latex] [latex]x[/latex]
7. [latex]sec[/latex] [latex]x[/latex]
9. [latex]csc[/latex] [latex]t[/latex]
11. −1
13. [latex]sec^2[/latex] [latex]x[/latex]
15. [latex]sin^2[/latex] [latex]x[/latex] + 1
17. [latex]\frac{1}{sin x}[/latex]
19. [latex]\frac{1}{cot x}[/latex]
21. [latex]tan[/latex] [latex]x[/latex]
23. −4 [latex]sec[/latex] [latex]x[/latex] [latex]tan[/latex] [latex]x[/latex]
25. ± [latex]\sqrt{\frac{{1}{cot^2 x}} + 1}[/latex]
27. ± [latex]\frac{\sqrt{1 − sin^2 x}}{sin x}[/latex]
29. Answers will vary. Sample proof:
31. Answers will vary. Sample proof:
33. Answers will vary. Sample proof:
35. False
37. False
39. Proved with negative and Pythagorean Identities.
41. True. Proof:
3 [latex]sin^2[/latex] [latex]θ[/latex] + 4 [latex]cos^2[/latex] [latex]θ[/latex] = 3 [latex]sin^2[/latex] [latex]θ[/latex] + 3 [latex]cos^2[/latex] [latex]θ[/latex] + [latex]cos^2[/latex] [latex]θ[/latex] = 3 ([latex]sin^2[/latex] [latex]θ[/latex] + [latex]cos^2[/latex] [latex]θ[/latex]) + [latex]cos^2[/latex] [latex]θ[/latex] = 3 + [latex]cos^2[/latex] [latex]θ[/latex]
Section 4.2 - Sum and Difference Identities
1. The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if one of those angles measures [latex]x[/latex], the second angle measures [latex]\frac{π}{2}[/latex] − [latex]x[/latex]. Then [latex]sin[/latex] [latex]x[/latex] = [latex]cos[/latex] ([latex]\frac{π}{2}[/latex] − [latex]x[/latex]). The same holds for the other cofunction identities. The key is that the angles are complementary.
3. [latex]sin[/latex] (−[latex]x[/latex]) = −[latex]sin[/latex] [latex]x[/latex], so [latex]sin[/latex] [latex]x[/latex] is odd. [latex]cos[/latex] (−[latex]x[/latex]) = [latex]cos[/latex] (0 − [latex]x[/latex]) = [latex]cos[/latex] [latex]x[/latex], so [latex]cos[/latex] [latex]x[/latex] is even.
5. [latex]\frac{\sqrt{2} + \sqrt{6}}{4}[/latex]
7. [latex]\frac{\sqrt{6} − \sqrt{2}}{4}[/latex]
9. −2 − [latex]\sqrt{3}[/latex]
11. −[latex]\frac{\sqrt{2}}{2}[/latex] [latex]sin[/latex] [latex]x[/latex] − [latex]\frac{\sqrt{2}}{2}[/latex] [latex]cos[/latex] [latex]x[/latex]
13. −[latex]\frac{1}{2}[/latex] [latex]cos[/latex] [latex]x[/latex] − [latex]\frac{\sqrt{3}}{2}[/latex] [latex]sin[/latex] [latex]x[/latex]
15. [latex]csc[/latex] [latex]θ[/latex]
17. [latex]cot[/latex] [latex]x[/latex]
19. [latex]tan[/latex] ([latex]\frac{x}{10}[/latex])
21. [latex]sin[/latex] ([latex]a[/latex] − [latex]b[/latex])= ([latex]\frac{4}{5}[/latex])([latex]\frac{1}{3}[/latex]) − ([latex]\frac{3}{5}[/latex])([latex]\frac{2\sqrt{2}}{3}[/latex]) = [latex]\frac{4 − 6\sqrt{2}}{15}[/latex]
[latex]cos[/latex] ([latex]a[/latex] + [latex]b[/latex])= ([latex]\frac{3}{5}[/latex])([latex]\frac{1}{3}[/latex]) − ([latex]\frac{4}{5}[/latex])([latex]\frac{2\sqrt{2}}{3}[/latex]) = [latex]\frac{3 − 8\sqrt{2}}{15}[/latex]
23. [latex]\frac{\sqrt{2} − \sqrt{6}}{4}[/latex]
25. [latex]sin[/latex] [latex]x[/latex]
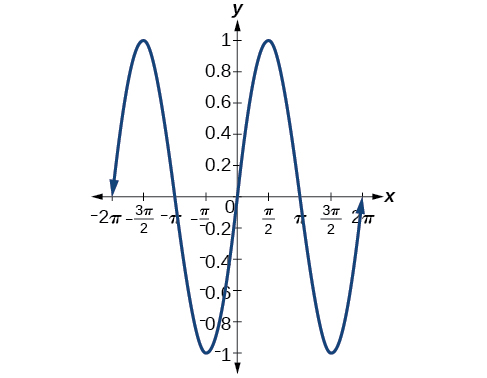
27. [latex]cot[/latex] ([latex]\frac{π}{6}[/latex] − [latex]x[/latex])
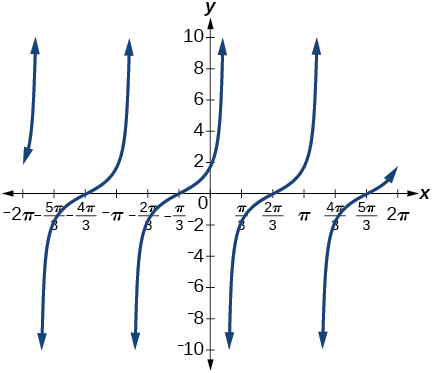
29. [latex]cot[/latex] ([latex]\frac{π}{4}[/latex] + [latex]x[/latex])
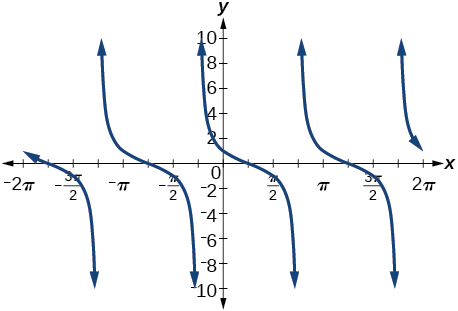
31. [latex]{sin x}{\sqrt{2}}[/latex] + [latex]{cos x}{\sqrt{2}}[/latex]
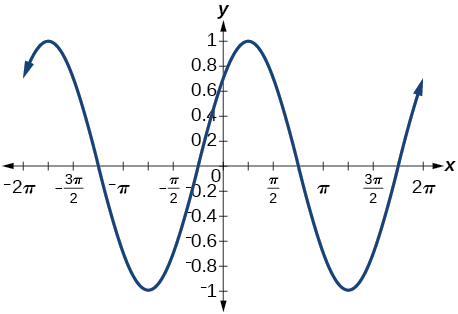
33. They are the same.
35. They are the different, try [latex]g[/latex]([latex]x[/latex]) = [latex]sin[/latex] ([latex]9x[/latex]) − [latex]cos[/latex]([latex]3x[/latex]) [latex]sin[/latex] ([latex]6x[/latex]).
37. They are the same.
39. They are the different, try [latex]g[/latex]([latex]θ[/latex]) = [latex]\frac{2 tan θ}{1 − tan^2 θ}[/latex].
41. They are different, try [latex]g[/latex]([latex]x[/latex]) =[latex]\frac{tan x − tan (2x)}{1 + tan (x) tan (2x)}[/latex].
43. True
45. True. Note that [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]) = [latex]sin[/latex] ([latex]π[/latex] − [latex]γ[/latex]) and expand the right hand side.
47.
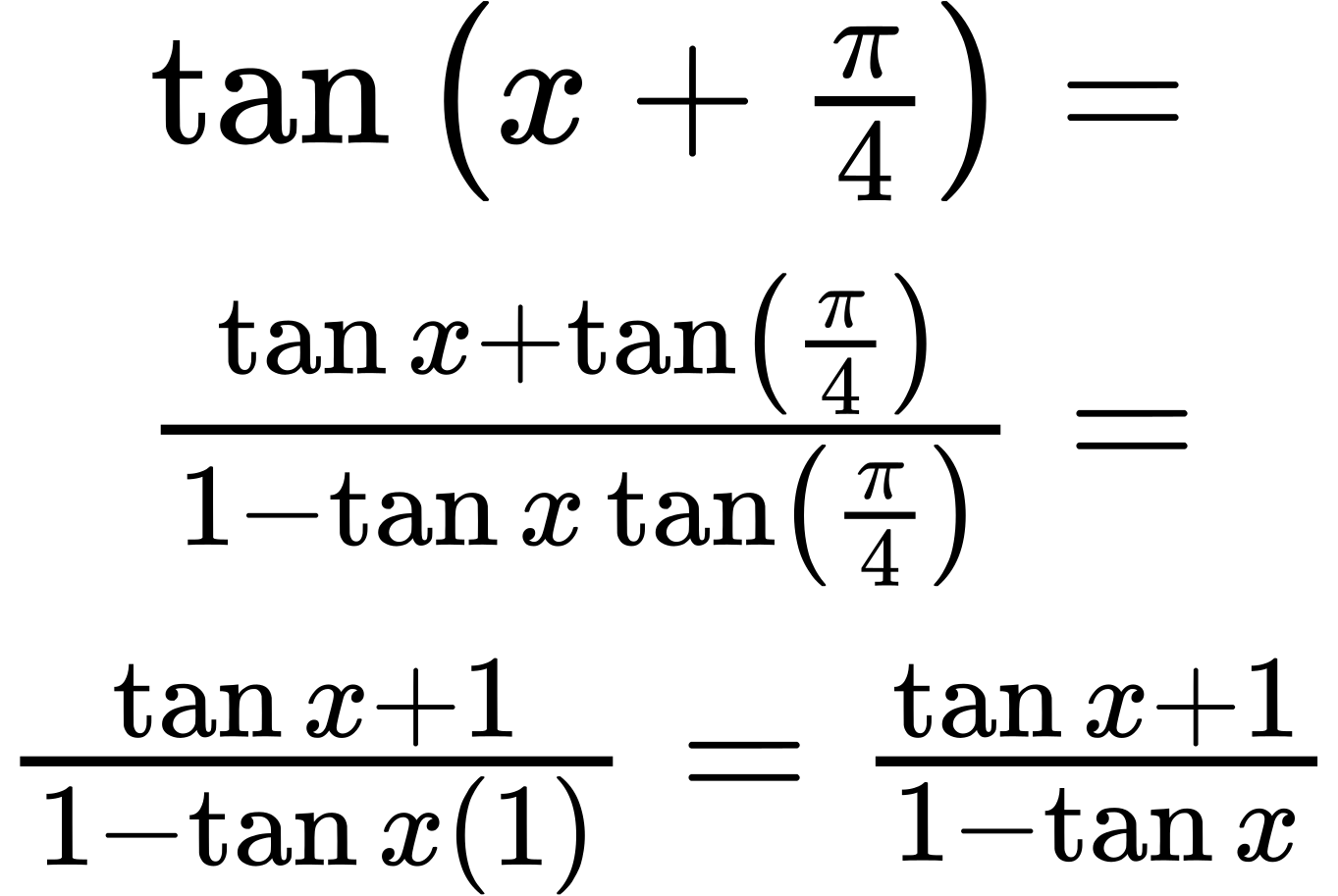
49.
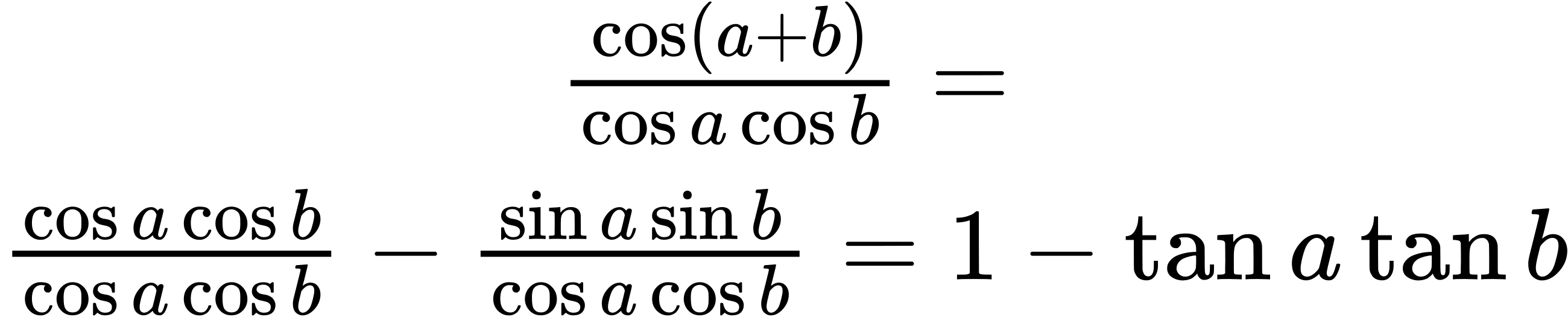
51.
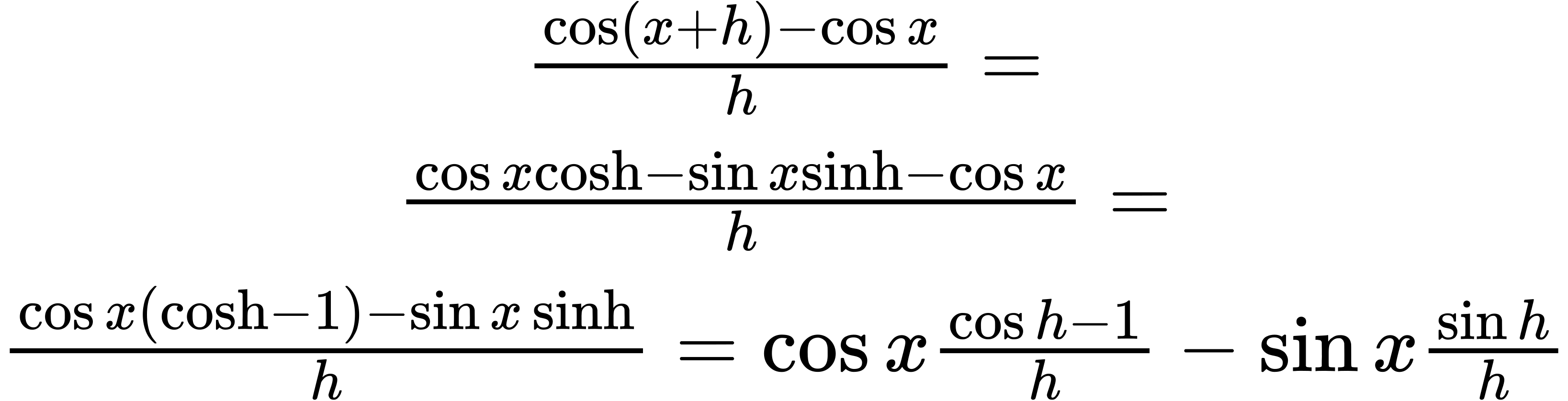
Section 4.3 - Double-Angle, Half-Angle, and Reduction Formulas
1. Use the Pythagorean identities and isolate the squared term.
3. [latex]\frac{1 − cos x}{sin x}[/latex], [latex]\frac{sin x}{1 + cos x}[/latex], multiplying the top and bottom by [latex]\sqrt{1 − cos x}[/latex] and [latex]\sqrt{1 + cos x}[/latex], respectively.
5. a) [latex]\frac{3\sqrt{7}}{32}[/latex], b) [latex]\frac{31}{32}[/latex], c) [latex]\frac{3\sqrt{7}}{31}[/latex]
7. a) [latex]\frac{\sqrt{3}}{2}[/latex], b) −[latex]\frac{1}{2}[/latex], c) −[latex]\sqrt{3}[/latex]
9. [latex]cos[/latex] [latex]θ[/latex] = −[latex]\frac{2\sqrt{5}}{5}[/latex], [latex]sin[/latex][latex]θ[/latex] = [latex]\frac{\sqrt{5}}{5}[/latex], [latex]tan[/latex][latex]θ[/latex] = −[latex]\frac{1}{2}[/latex], [latex]csc[/latex][latex]θ[/latex] = [latex]\sqrt{5}[/latex], [latex]sec[/latex] [latex]θ[/latex] = −[latex]\frac{\sqrt{5}}{2}[/latex], [latex]cot[/latex] [latex]θ[/latex] = −2
11. 2 [latex]sin[/latex] ([latex]\frac{π}{2})[/latex]
13. [latex]\frac{\sqrt{2 − \sqrt{2}}}{2}[/latex]
15. [latex]\frac{\sqrt{2 − \sqrt{3}}}{2}[/latex]
17. 2 + [latex]\sqrt{3}[/latex]
19. −1 −[latex]\sqrt{2}[/latex]
21. a) [latex]\frac{3\sqrt{13}}{13}[/latex], b) −[latex]\frac{2\sqrt{13}}{13}[/latex], c) −[latex]\frac{3}{2}[/latex]
23. a) [latex]\frac{\sqrt{10}}{4}[/latex], b) [latex]\frac{\sqrt{6}}{4}[/latex], c) [latex]\frac{\sqrt{15}}{3}[/latex]
25. [latex]\frac{120}{169}[/latex], –[latex]\frac{119}{169}[/latex], –[latex]\frac{120}{119}[/latex]
27. [latex]\frac{2\sqrt{13}}{13}[/latex], −[latex]\frac{3\sqrt{13}}{13}[/latex], −[latex]\frac{2}{3}[/latex]
29. [latex]cos[/latex] (74°)
31. [latex]cos[/latex] (18[latex]x[/latex])
33. 3 [latex]sin[/latex] (10[latex]x[/latex])
35. −2 [latex]sin[/latex] (−[latex]x[/latex]) [latex]cos[/latex] (−[latex]x[/latex]) = −2(−[latex]sin[/latex] ([latex]x[/latex]) [latex]cos[/latex] ([latex]x[/latex])) = [latex]sin[/latex] (2[latex]x[/latex])
37.
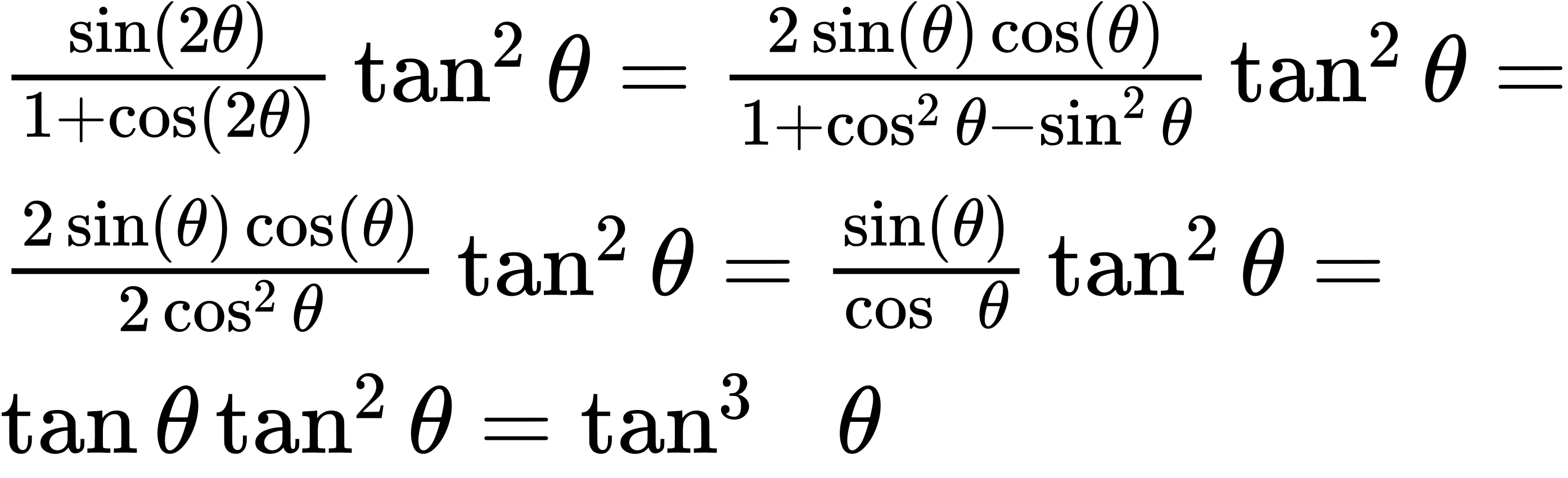
39. [latex]\frac{1 + cos (12x)}{2}[/latex]
41. [latex]\frac{3 + cos (12x) − 4 cos (6x)}{8}[/latex]
43. [latex]\frac{2 + cos (2x) −2 cos (4x) − cos (6x)}{32}[/latex]
45. [latex]\frac{2 tan x}{1 + tan^2 x}[/latex] = [latex]\frac{\frac{2 sin x}{cos x}}{1 + \frac{sin^2 x}{cos^2 x}}[/latex] = [latex]\frac{\frac{2sin x}{cos x}}{\frac{cos^2 x + sin^2 x}{cos^2 x}}[/latex] = [latex]\frac{2sin x}{cos x}[/latex] ([latex]\frac{cos^2 x}{1}[/latex]) = 2 [latex]sin[/latex] [latex]x[/latex] [latex]cos[/latex] [latex]x[/latex] = [latex]sin[/latex] ([latex]2x[/latex])
47. [latex]\frac{2 sin x cos x}{2 cos^2 x − 1}[/latex] = [latex]\frac{sin (2x)}{cos (2x)}[/latex] = [latex]tan[/latex] (2[latex]x[/latex])
49.
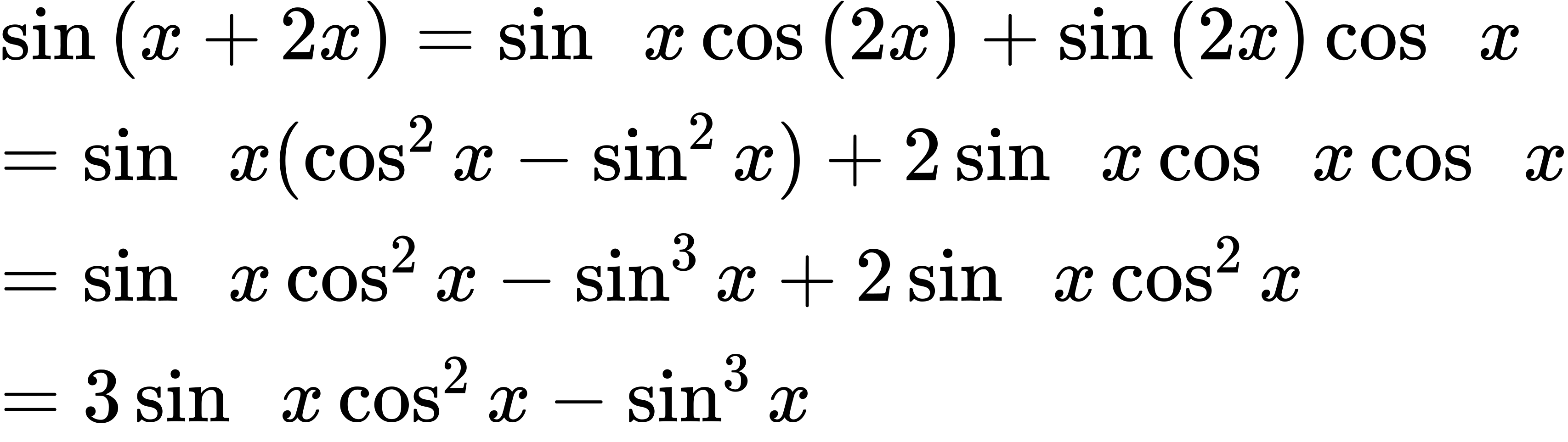
51.
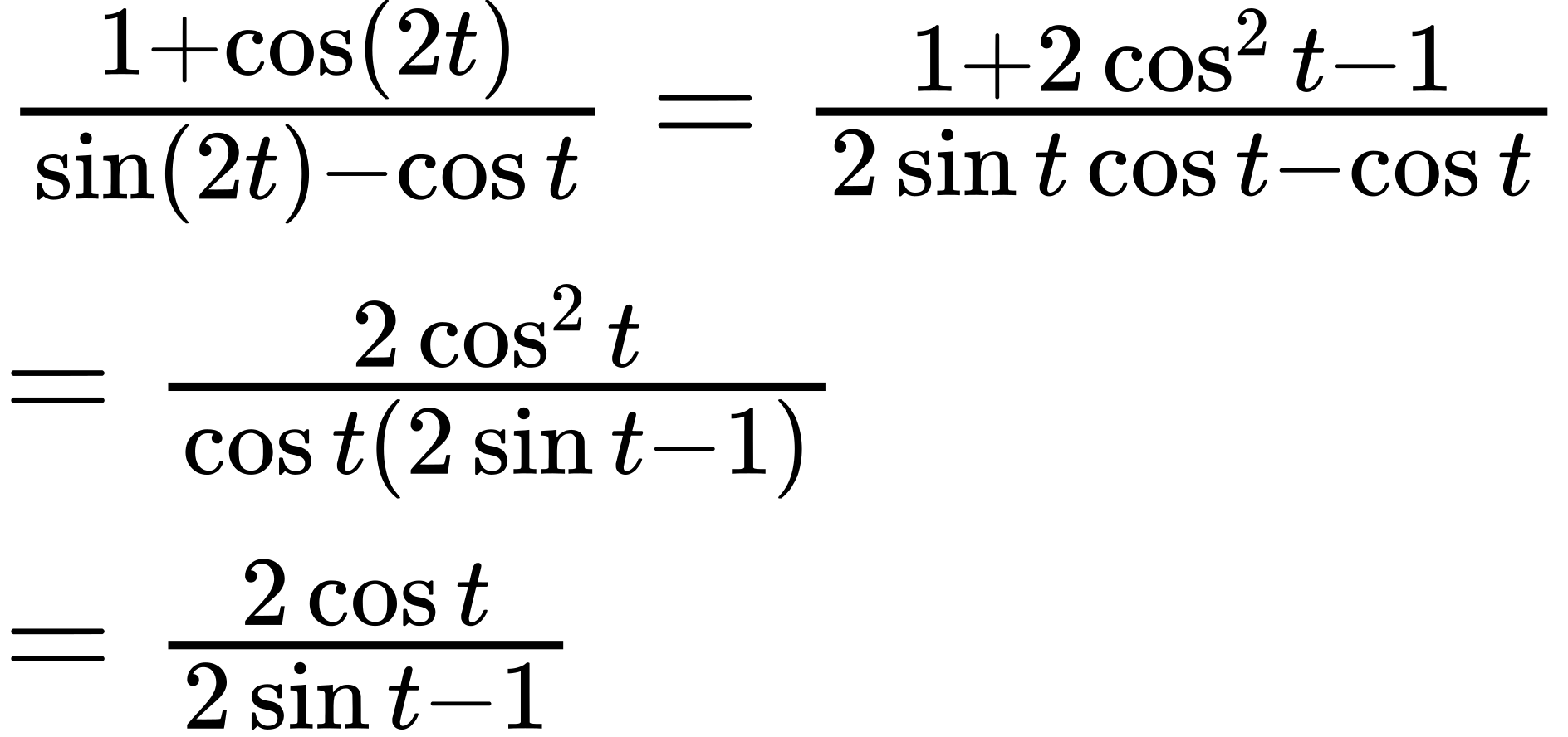
53.
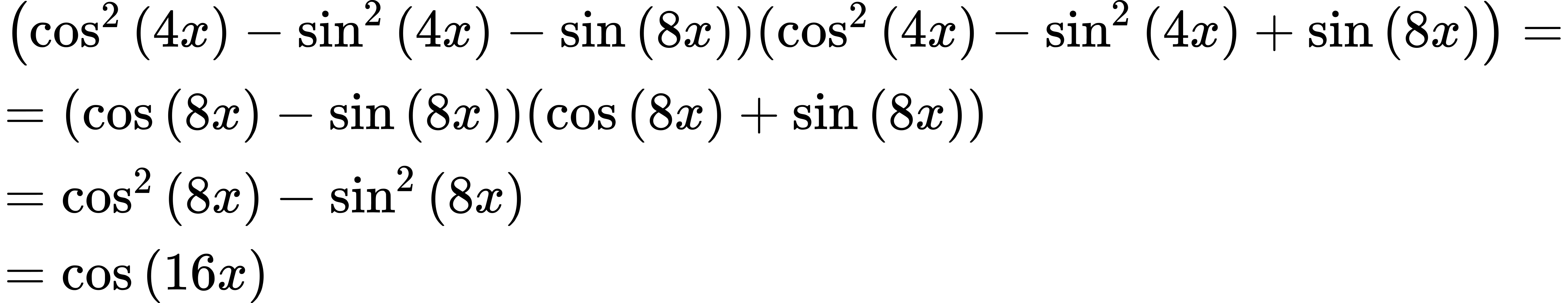
Section 4.4 - Sum-to-Product and Product-to-Sum Formulas
1. Substitute [latex]α[/latex] into cosine and [latex]β[/latex] into sine and evaluate.
3. Answers will vary. There are some equations that involve a sum of two trig expressions where when converted to a product are easier to solve. For example: [latex]\frac{sin (3x) + sin x}{cos x}[/latex] = 1. When converting the numerator to a product the equation becomes: [latex]\frac{2 sin (2x) cos x}{cos x}[/latex] = 1 .
5. 8 ([latex]cos[/latex] (5[latex]x[/latex]) − [latex]cos[/latex] (27[latex]x[/latex]))
7. [latex]sin[/latex] (2[latex]x[/latex]) + [latex]sin[/latex] (8[latex]x[/latex])
9. [latex]\frac{1}{2}[/latex] ([latex]cos[/latex] (6[latex]x[/latex]) − [latex]cos[/latex] (4[latex]x[/latex]))
11. 2 [latex]cos[/latex] (5[latex]t[/latex]) [latex]cos[/latex] [latex]t[/latex]
13. 2 [latex]cos[/latex] (7[latex]x[/latex])
15. 2 [latex]cos[/latex] (6[latex]x[/latex]) [latex]cos[/latex] (3[latex]x[/latex])
17. [latex]\frac{1}{4}[/latex] (1 + [latex]\sqrt{3}[/latex])
19. [latex]\frac{1}{4}[/latex] ([latex]\sqrt{3}[/latex] − 2)
21. [latex]\frac{1}{4}[/latex] ([latex]\sqrt{3}[/latex] − 1)
23. [latex]cos[/latex] (80°) − [latex]cos[/latex] (120°)
25. 12 ([latex]sin[/latex] (221°) + [latex]sin[/latex] (205°))
27. [latex]\sqrt{2}[/latex] [latex]cos[/latex] (31°)
29. 2 [latex]cos[/latex] (66.5°) [latex]sin[/latex] (34.5°)
31. 2 [latex]sin[/latex] (−1.5°) [latex]cos[/latex] (0.5°)
33.
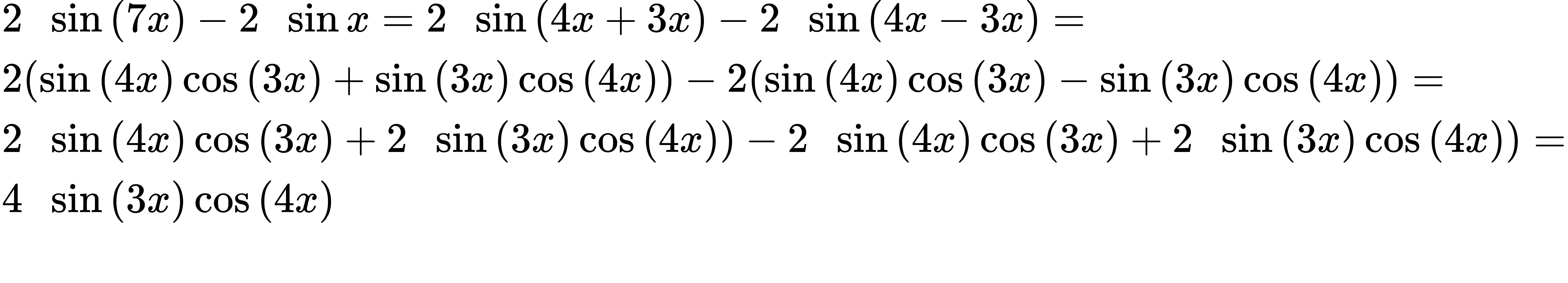
35. [latex]sin[/latex] [latex]x[/latex] + [latex]sin[/latex] (3[latex]x[/latex]) = 2 [latex]sin[/latex] ([latex]\frac{4x}{2}[/latex]) [latex]cos[/latex] ([latex]\frac{−2x}{2}[/latex]) = 2 [latex]sin[/latex](2[latex]x[/latex]) [latex]cos[/latex] [latex]x[/latex] = 2 (2 [latex]sin[/latex] [latex]x[/latex] [latex]cos[/latex] [latex]x[/latex]) [latex]cos[/latex] [latex]x[/latex] = 4 [latex]sin[/latex] [latex]x[/latex] [latex]cos^2[/latex] [latex]x[/latex]
37. 2 [latex]tan[/latex] [latex]x[/latex] [latex]cos[/latex] (3[latex]x[/latex]) = [latex]\frac{2 sin x cos (3x)}{cos x}[/latex] = [latex]\frac{2 (.5 (sin (4x) − sin (2x)))}{cos x}[/latex] = [latex]\frac{1}{cos x}[/latex] ([latex]sin[/latex] (4[latex]x[/latex]) − [latex]sin[/latex] (2[latex]x[/latex])) = [latex]sec[/latex] [latex]x[/latex] ([latex]sin[/latex] (4[latex]x[/latex]) − [latex]sin[/latex] (2[latex]x[/latex]))
39. 2 [latex]cos[/latex] (35°) [latex]cos[/latex] (23°), 1.5081
41. −2 [latex]sin[/latex] (33°) [latex]sin[/latex] (11°), −0.2078
43. [latex]\frac{1}{2}[/latex] ([latex]cos[/latex] (99°) − [latex]cos[/latex] (71°)), −0.2410
45. Start with [latex]cos[/latex] [latex]x[/latex] + [latex]cos[/latex] [latex]y[/latex]. Make a substitution and let [latex]x[/latex] = [latex]α[/latex] + [latex]β[/latex] and let [latex]y[/latex] = [latex]α[/latex] − [latex]β[/latex], so [latex]cos[/latex] [latex]x[/latex] + [latex]cos[/latex] [latex]y[/latex] becomes [latex]cos[/latex] ([latex]α[/latex] + [latex]β[/latex]) + [latex]cos[/latex] ([latex]α[/latex] − [latex]β[/latex]) = [latex]cos[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] − [latex]sin[/latex] [latex]α[/latex] [latex]sin[/latex] [latex]β[/latex] + [latex]cos[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] + [latex]sin[/latex] [latex]α[/latex] [latex]sin[/latex] [latex]β[/latex] = 2 [latex]cos[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] . Since [latex]x[/latex] = [latex]α[/latex] + [latex]β[/latex] and [latex]y[/latex] = [latex]α[/latex] − [latex]β[/latex], we can solve for [latex]α[/latex] and [latex]β[/latex] in terms of x and y and substitute in for 2 [latex]cos[/latex] [latex]α[/latex] [latex]cos[/latex] [latex]β[/latex] and get 2 [latex]cos[/latex] ([latex]\frac{x + y}{2}[/latex]) [latex]cos[/latex] ([latex]\frac{x−y}{2}[/latex]).
47. [latex]\frac{cos (3x) + cos x}{cos (3x) − cos x}[/latex] = [latex]\frac{2 cos (2x) cos x}{−2 sin (2x) sin x}[/latex] = − [latex]cot[/latex] (2[latex]x[/latex]) [latex]cot[/latex] [latex]x[/latex]
49.
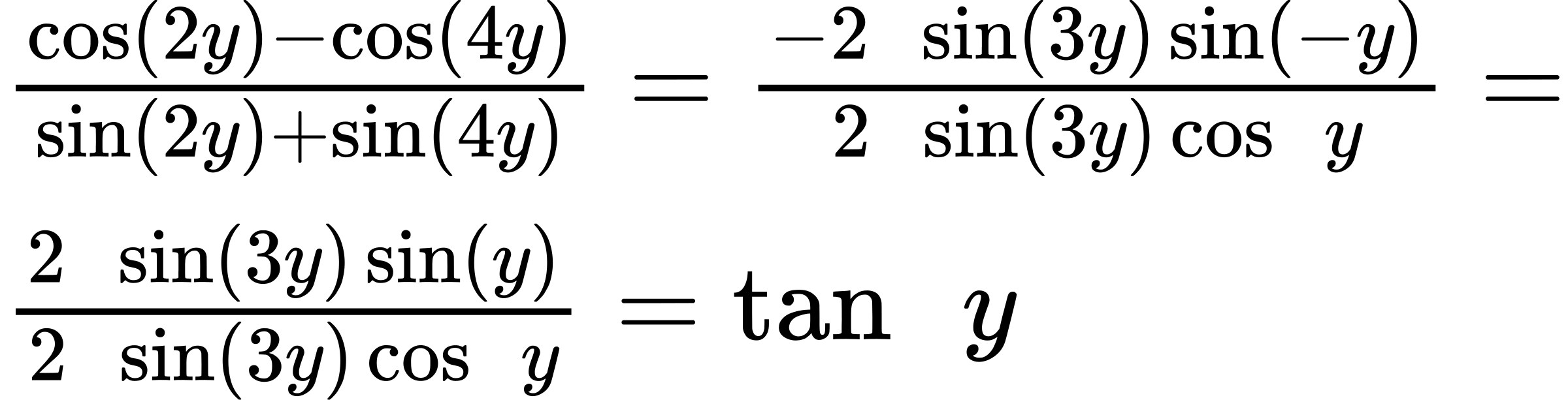
51.
![]()
53. [latex]tan[/latex] ([latex]\frac{π}{4}[/latex] − [latex]t[/latex]) = [latex]\frac{tan (\frac{π}{4}) − \text{tan t}}{1 + tan (\frac{π}{4}) tan (t)}[/latex] = [latex]\frac{1 − \text{tan t}}{1 + \text{tan t}}[/latex]
Section 4.5 - Solving Trigonometric Equations
1. There will not always be solutions to trigonometric function equations. For a basic example, [latex]cos[/latex] ([latex]x[/latex]) = −5.
3. If the sine or cosine function has a coefficient of one, isolate the term on one side of the equals sign. If the number it is set equal to has an absolute value less than or equal to one, the equation has solutions, otherwise it does not. If the sine or cosine does not have a coefficient equal to one, still isolate the term but then divide both sides of the equation by the leading coefficient. Then, if the number it is set equal to has an absolute value greater than one, the equation has no solution.
5. [latex]\frac{π}{3}[/latex], [latex]\frac{2π}{3}[/latex]
7. [latex]\frac{3π}{4}[/latex], [latex]\frac{5π}{4}[/latex]
9. [latex]\frac{π}{4}[/latex], [latex]\frac{5π}{4}[/latex]
11. [latex]\frac{π}{4}[/latex], [latex]\frac{3π}{4}[/latex], [latex]\frac{5π}{4}[/latex], [latex]\frac{7π}{4}[/latex]
13. [latex]\frac{π}{4}[/latex], [latex]\frac{7π}{4}[/latex]
15. [latex]\frac{7π}{6}[/latex], [latex]\frac{11π}{6}[/latex]
17. [latex]\frac{π}{18}[/latex], [latex]\frac{5π}{18}[/latex], [latex]\frac{13π}{18}[/latex], [latex]\frac{17π}{18}[/latex], [latex]\frac{25π}{18}[/latex], [latex]\frac{29π}{18}[/latex]
19. [latex]\frac{3π}{12}[/latex], [latex]\frac{5π}{12}[/latex], [latex]\frac{11π}{12}[/latex], [latex]\frac{13π}{12}[/latex], [latex]\frac{19π}{12}[/latex], [latex]\frac{21π}{12}[/latex]
21. [latex]\frac{1}{6}[/latex], [latex]\frac{5}{6}[/latex], [latex]\frac{13}{6}[/latex], [latex]\frac{17}{6}[/latex], [latex]\frac{25}{6}[/latex], [latex]\frac{29}{6}[/latex], [latex]\frac{37}{6}[/latex]
23. 0, [latex]\frac{π}{3}[/latex], [latex]π[/latex], [latex]\frac{5π}{3}[/latex]
25. [latex]\frac{π}{3}[/latex], [latex]π[/latex], [latex]\frac{5π}{3}[/latex]
27. [latex]\frac{π}{3}[/latex], [latex]\frac{3π}{2}[/latex], [latex]\frac{5π}{3}[/latex]
29. 0, [latex]π[/latex]
31. [latex]π[/latex] − [latex]sin^{−1}[/latex] (−[latex]\frac{1}{4}[/latex]), [latex]\frac{7π}{6}[/latex], [latex]\frac{11π}{6}[/latex], [latex]2π[/latex] + [latex]sin^{−1}[/latex] (−[latex]\frac{1}{4}[/latex])
33. [latex]\frac{1}{3}[/latex] ([latex]sin^{−1}[/latex] ([latex]\frac{9}{10}[/latex])), [latex]\frac{π}{3}[/latex] − [latex]\frac{1}{3}[/latex] ([latex]sin^{−1}[/latex] ([latex]\frac{9}{10}[/latex])), [latex]\frac{2π}{3}[/latex] + [latex]\frac{1}{3}[/latex] ([latex]sin^{−1}[/latex] ([latex]\frac{9}{10}[/latex])), [latex]π[/latex] − [latex]\frac{1}{3}[/latex] ([latex]sin^{−1}[/latex] ([latex]\frac{9}{10}[/latex])), [latex]\frac{4π}{3}[/latex] + [latex]\frac{1}{3}[/latex] ([latex]sin^{−1}[/latex] ([latex]\frac{9}{10}[/latex])), [latex]\frac{5π}{3}[/latex] − [latex]\frac{1}{3}[/latex] ([latex]sin^{−1}[/latex] ([latex]\frac{9}{10}[/latex]))
35. 0
37. [latex]θ[/latex] = [latex]sin^{−1}[/latex] ([latex]\frac{2}{3}[/latex]), [latex]π[/latex] − [latex]sin^{−1}[/latex] ([latex]\frac{2}{3}[/latex]), [latex]π[/latex] + [latex]sin^{−1}[/latex] ([latex]\frac{2}{3}[/latex]), [latex]2π[/latex] − [latex]sin^{−1}[/latex] ([latex]\frac{2}{3}[/latex])
39. [latex]\frac{3π}{2}[/latex], [latex]\frac{π}{6}[/latex], [latex]\frac{5π}{6}[/latex]
41. 0, [latex]\frac{π}{3}[/latex], [latex]π[/latex], [latex]\frac{4π}{3}[/latex]
43. There are no solutions.
45. [latex]cos^{−1}[/latex] ([latex]\frac{1}{3}[/latex] (1 − [latex]\sqrt{7}[/latex])), [latex]2π[/latex] − [latex]cos^{−1}[/latex] ([latex]\frac{1}{3}[/latex] (1 − [latex]\sqrt{7}[/latex]))
47. [latex]tan^{−1}[/latex] ([latex]\frac{1}{2}[/latex] ([latex]\sqrt{29}[/latex] − 5)), [latex]π[/latex] + [latex]tan^{−1}[/latex] ([latex]\frac{1}{2}[/latex] (−[latex]\sqrt{29}[/latex] − 5)), [latex]π[/latex] + [latex]tan^{−1}[/latex] ([latex]\frac{1}{2}[/latex] ([latex]\sqrt{29}[/latex] − 5)), [latex]2π[/latex] + [latex]tan^{−1}[/latex] ([latex]\frac{1}{2}[/latex] (−[latex]\sqrt{29}[/latex] − 5))
49. There are no solutions.
51. There are no solutions.
53. 0, [latex]\frac{2π}{3}[/latex], [latex]\frac{4π}{3}[/latex]
55. [latex]\frac{π}{4}[/latex], [latex]\frac{3π}{4}[/latex], [latex]\frac{5π}{4}[/latex], [latex]\frac{7π}{4}[/latex]
57. [latex]sin^{−1}[/latex] ([latex]\frac{3}{5}[/latex]), [latex]\frac{π}{2}[/latex], [latex]π[/latex] − [latex]sin^{−1}[/latex] ([latex]\frac{3}{5}[/latex]), [latex]\frac{3π}{2}[/latex]
59. [latex]cos^{−1}[/latex] (−[latex]\frac{1}{4}[/latex]), [latex]2π[/latex] − [latex]cos^{−1}[/latex] (−[latex]\frac{1}{4}[/latex])
61. [latex]\frac{π}{3}[/latex], [latex]cos^{−1}[/latex] (−[latex]\frac{3}{4}[/latex]), [latex]2π[/latex] − [latex]cos^{−1}[/latex] (−[latex]\frac{3}{4}[/latex]), [latex]\frac{5π}{3}[/latex]
63. [latex]cos^{−1}[/latex] ([latex]\frac{3}{4}[/latex]), [latex]cos^{−1}[/latex] (−[latex]\frac{2}{3}[/latex]), [latex]2π[/latex] − [latex]cos^{−1}[/latex] (−[latex]\frac{2}{3}[/latex]), [latex]2π[/latex] − [latex]cos^{−1}[/latex] (−[latex]\frac{3}{4}[/latex])
65. 0, [latex]\frac{π}{2}[/latex], [latex]π[/latex], [latex]\frac{3π}{2}[/latex]
67. [latex]\frac{π}{3}[/latex], [latex]cos^{−1}[/latex] (−[latex]\frac{1}{4}[/latex]), [latex]2π[/latex] − [latex]cos^{−1}[/latex] (−[latex]\frac{1}{4}[/latex]), [latex]\frac{5π}{3}[/latex]
69. There are no solutions.
71. [latex]π[/latex] + [latex]tan^{−1}[/latex] (−2), [latex]π[/latex] + [latex]tan^{−1}[/latex] (−[latex]\frac{3}{2}[/latex]), [latex]2π[/latex] + [latex]tan^{−1}[/latex] (−2), [latex]2π[/latex] + [latex]tan^{−1}[/latex] (−[latex]\frac{3}{2}[/latex])
73. [latex]sin^{−1}[/latex] ([latex]\frac{1}{4}[/latex]), [latex]π[/latex] − [latex]sin^{−1}[/latex] ([latex]\frac{1}{4}[/latex]), [latex]\frac{3π}{2}[/latex]
75. [latex]\frac{π}{2}[/latex], [latex]\frac{3π}{2}[/latex]
77. There are no solutions.
79. 0, [latex]\frac{π}{2}[/latex], [latex]π[/latex], [latex]\frac{3π}{2}[/latex]
81. There are no solutions.
83. 7.2°
85. 5.7°
87. 82.4°
89. 31.0°
91. 88.7°
93. 59.0°
95. 36.9°

