“Try It” Exercises

Section 2.1 – Angles

1.

2. [latex]\frac{3π}{2}[/latex]

3. −135°

4. [latex]\frac{7π}{10}[/latex]

5. [latex]α[/latex] = 150°

6. [latex]β[/latex] = 60​°

7. [latex]\frac{7π}{6}[/latex]

8. [latex]\frac{215π}{8}[/latex] = 37.525 units

9. 1.88

10. −[latex]\frac{3π}{2}[/latex] rad/s

11. 1655 kilometers per hour

Section 2.2 – Unit Circle: Sine and Cosine Functions

1. [latex]cos(t)[/latex] = −[latex]\frac{\sqrt{2}}{2}[/latex], [latex]sin(t)[/latex] = [latex]\frac{\sqrt{2}}{2}[/latex]

2. [latex]cos(π)[/latex] = −1, [latex]sin(π)[/latex] = 0

3. [latex]sin(t)[/latex] = −[latex]\frac{7}{25}[/latex]

4. [latex]\frac{π}{3}[/latex]

5. ⓐ [latex]cos[/latex](315​°) = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]sin[/latex](315​°) = –[latex]\frac{\sqrt{2}}{2}[/latex]

    ⓑ [latex]cos[/latex](−[latex]\frac{π}{6}[/latex]) = [latex]\frac{\sqrt{3}}{2}[/latex], [latex]sin[/latex](−[latex]\frac{π}{6}[/latex]) = −[latex]\frac{1}{2}[/latex]

6. ([latex]\frac{1}{2}[/latex], −[latex]\frac{\sqrt{3}}{2}[/latex])

Section 2.3 – The Other Trigonometric Functions

1. [latex]sin t[/latex] = −[latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos t[/latex] = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]tan t[/latex] = −1, [latex]sec t[/latex] = [latex]\sqrt{2}[/latex], [latex]csc t[/latex] = −[latex]\sqrt{2}[/latex], [latex]cot t[/latex] = −1

2. [latex]sin[/latex] [latex]\frac{π}{3}[/latex] = [latex]\frac{\sqrt{3}}{2}[/latex], [latex]cos[/latex] [latex]\frac{π}{3}[/latex] = [latex]\frac{1}{2}[/latex], [latex]tan[/latex] [latex]\frac{π}{3}[/latex]= [latex]\sqrt{3}[/latex], [latex]sec[/latex] [latex]\frac{π}{3}[/latex] = 2, [latex]csc[/latex] [latex]\frac{π}{3}[/latex] = [latex]\frac{2\sqrt{3}}{3}[/latex], [latex]cot[/latex] [latex]\frac{π}{3}[/latex] = [latex]\frac{\sqrt{3}}{3}[/latex]

3. [latex]sin[/latex] (−[latex]\frac{7π}{4}[/latex]) = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos[/latex] (−[latex]\frac{7π}{4}[/latex]) = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]tan[/latex] (−[latex]\frac{7π}{4}[/latex]) = 1,

[latex]sec[/latex] −([latex]\frac{7π}{4}[/latex]) = [latex]\sqrt{2}[/latex], [latex]csc[/latex] (−[latex]\frac{7π}{4}[/latex]) = [latex]\sqrt{2}[/latex], [latex]cot[/latex] (−[latex]\frac{7π}{4}[/latex]) = 1

4. −[latex]\sqrt{3}[/latex]

5. −[latex]\sqrt{2}[/latex]

6. [latex]sin t[/latex]

7. [latex]cos t[/latex] = −[latex]\frac{8}{17}[/latex], [latex]sin t[/latex] = [latex]\frac{15}{17}[/latex], [latex]tan t[/latex] = −[latex]\frac{15}{8}[/latex], [latex]csc t[/latex] = [latex]\frac{17}{15}[/latex], [latex]cot t[/latex] = −[latex]\frac{8}{15}[/latex]

8.

 

 

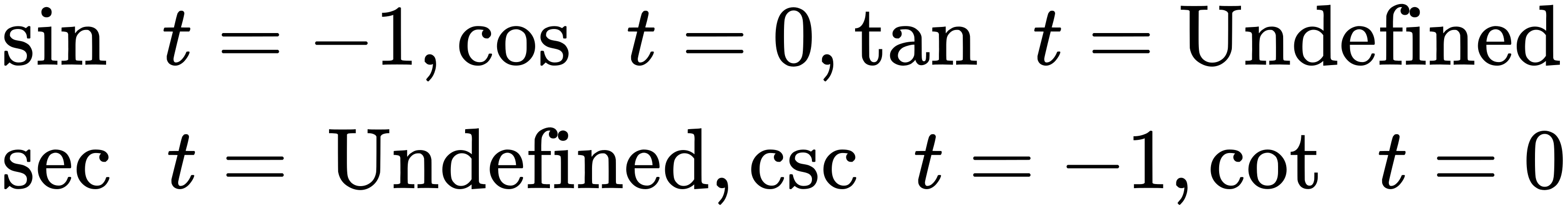
9. [latex]sec t[/latex] = [latex]\sqrt{2}[/latex], [latex]csc t[/latex] = [latex]\sqrt{2}[/latex], [latex]tan t[/latex] = 1, [latex]cot t[/latex] = 1

Section 2.4 – Right Triangle Trigonometry

1. [latex]\frac{7}{25}[/latex]

2.

 

 

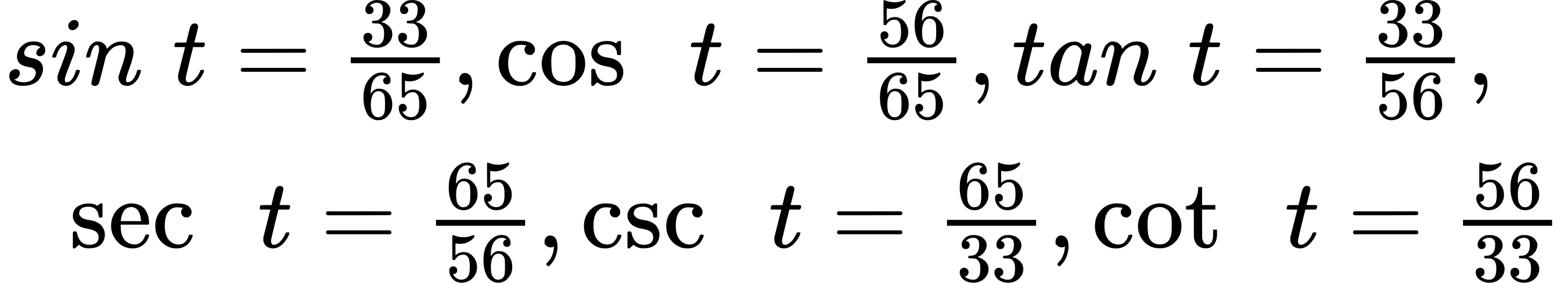
3. [latex]sin[/latex] ([latex]\frac{π}{4}[/latex]) = [latex]\frac{1}{\sqrt{2}}[/latex], [latex]cos[/latex] ([latex]\frac{π}{4}[/latex]) = [latex]\frac{1}{\sqrt{2}}[/latex], [latex]tan[/latex]([latex]\frac{π}{4}[/latex]) = 1,

[latex]sec[/latex] ([latex]\frac{π}{4}[/latex]) = [latex]\sqrt{2}[/latex], [latex]csc[/latex] ([latex]\frac{π}{4}[/latex]) = [latex]\sqrt{2}[/latex], [latex]cot[/latex] ([latex]\frac{π}{4}[/latex]) = 1

4. 2

5. adjacent = [latex]10[/latex]; opposite = [latex]10\sqrt{3}[/latex]; missing angle is [latex]\frac{π}{6}[/latex]

6. About 52 ft

Section Exercises

Section 2.1 – Angles

1.

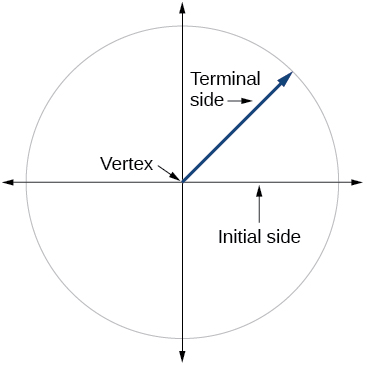
3. Whether the angle is positive or negative determines the direction. A positive angle is drawn in the counterclockwise direction, and a negative angle is drawn in the clockwise direction.

5. Linear speed is a measurement found by calculating distance of an arc compared to time. Angular speed is a measurement found by calculating the angle of an arc compared to time.

7.

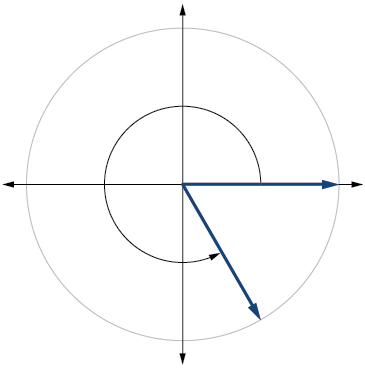
9.

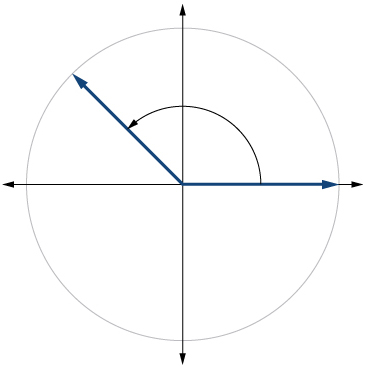
11.

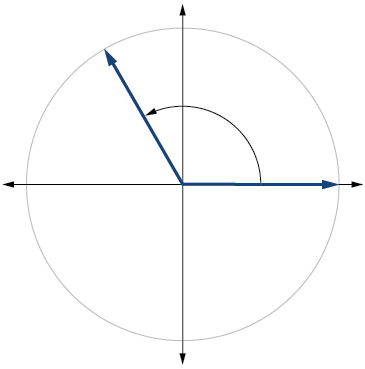
13.

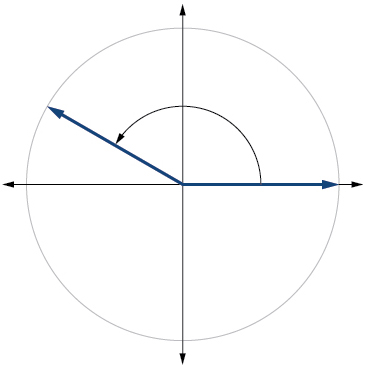
15.

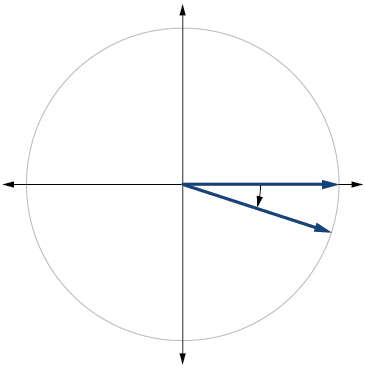
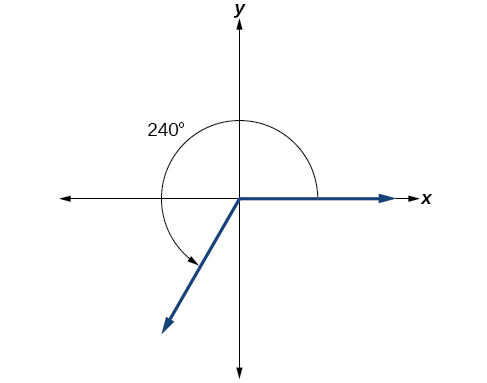
17. 240°

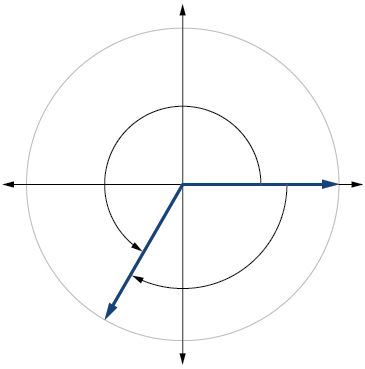
19. [latex]\frac{4π}{3}[/latex]

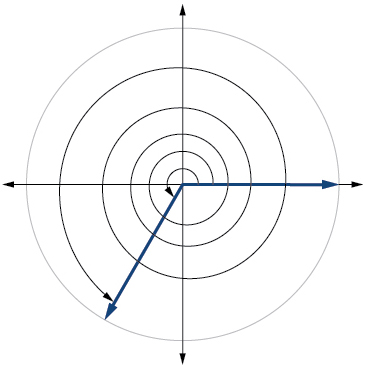
21. [latex]\frac{2π}{3}[/latex]

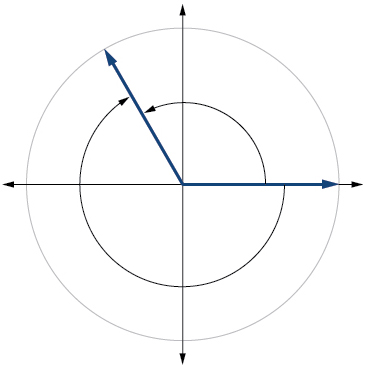
23. [latex]\frac{7π}{2}[/latex] ≈ 11.00 in²

25. [latex]\frac{81π}{20}[/latex] ≈ 12.72 cm²

27. 20°

29. 60°

31. −75°

33. [latex]\frac{π}{2}[/latex] radians

35. −[latex]3π[/latex] radians

37. [latex]π[/latex] radians

39. [latex]\frac{5π}{6}[/latex] radians

41. [latex]\frac{5.02π}{3}[/latex] ≈ 5.26 miles

43. [latex]\frac{25π}{9}[/latex] ≈ 8.73 centimeters

45. [latex]\frac{21π}{10}[/latex] ≈ 6.60 meters

47. 104.7198 cm²

49. 0.7697 in²

51. 250°

53. 320°

55. [latex]\frac{4π}{3}[/latex]

57. [latex]\frac{8π}{9}[/latex]

59. 1320 rad 210.085 RPM

61. 7 in./s, 4.77 RPM, 28.65 deg/s

63. 1,809,557.37 mm/min=30.16 m/s

65. 5.76 miles

67. 120°

69. 794 miles per hour

71. 2,234 miles per hour

73. 11.5 inches

Section 2.2 – Unit Circle: Sine and Cosine Functions

1. The unit circle is a circle of radius 1 centered at the origin.

3. Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis.

5. The sine values are equal.

7. I

9. IV

11. [latex]\frac{\sqrt{3}}{2}[/latex]

13. [latex]\frac{1}{2}[/latex]

15. [latex]\frac{\sqrt{2}}{3}[/latex]

17. 0

19. −1

21. [latex]\frac{\sqrt{3}}{2}[/latex]

23. 60​°

25. 80​°

27. 45​°

29. [latex]\frac{π}{3}[/latex]

31. [latex]\frac{π}{3}[/latex]

33. [latex]\frac{π}{8}[/latex]

35. 60​°, Quadrant IV, [latex]sin[/latex] (300​°) = −[latex]\frac{\sqrt{3}}{2}[/latex], [latex]cos[/latex] (300°) = [latex]\frac{1}{2}[/latex]

37. 45​°, Quadrant II, [latex]sin[/latex] (135​°) = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos[/latex] (135​°) = −[latex]\frac{\sqrt{2}}{2}[/latex]

39. 60​°, Quadrant II, [latex]sin[/latex] (120​°) = [latex]\frac{\sqrt{3}}{2}[/latex], [latex]cos[/latex] (120​°) = −[latex]\frac{1}{2}[/latex] 

41. 30​°, Quadrant II, [latex]sin[/latex] (150​°) = [latex]\frac{1}{2}[/latex], [latex]cos[/latex] (150​°) = −[latex]\frac{\sqrt{3}}{2}[/latex]

43. [latex]\frac{π}{6}[/latex], Quadrant III, [latex]sin[/latex] ([latex]\frac{7π}{6}[/latex]) = −[latex]\frac{1}{2}[/latex], [latex]cos[/latex] ([latex]\frac{7π}{6}[/latex]) = −[latex]\frac{\sqrt{3}}{2}[/latex]

45. [latex]\frac{π}{4}[/latex], Quadrant II, [latex]sin[/latex] ([latex]\frac{3π}{4}[/latex]) = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos[/latex] ([latex]\frac{3π}{4}[/latex]) = −[latex]\frac{\sqrt{2}}{2}[/latex]

47. [latex]\frac{π}{3}[/latex], Quadrant II, [latex]sin[/latex] ([latex]\frac{2π}{3}[/latex]) = [latex]\frac{\sqrt{3}}{2}[/latex], [latex]cos[/latex] ([latex]\frac{2π}{3}[/latex]) = −[latex]\frac{1}{2}[/latex]

49. [latex]\frac{π}{4}[/latex], Quadrant IV, [latex]sin[/latex] ([latex]\frac{7π}{4}[/latex]) = −[latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos[/latex] ([latex]\frac{7π}{4}[/latex]) = [latex]\frac{\sqrt{2}}{2}[/latex]

51. [latex]\frac{\sqrt{77}}{9}[/latex]

53. −[latex]\frac{\sqrt{15}}{4}[/latex] 

55. (−10, [latex]10\sqrt{3}[/latex])

57. (–2.778, 15.757)

59. [–1, 1]

61. [latex]sin t[/latex] = [latex]\frac{1}{2}[/latex], [latex]cos t[/latex] = −[latex]\frac{\sqrt{3}}{2}[/latex]

63. [latex]sin t[/latex] = −[latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos t[/latex] = −[latex]\frac{\sqrt{2}}{2}[/latex]

65. [latex]sin t[/latex] = [latex]\frac{\sqrt{3}}{2}[/latex], [latex]cos t[/latex] = −[latex]\frac{1}{2}[/latex]

67. [latex]sin t[/latex] = −[latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos t[/latex] = [latex]\frac{\sqrt{2}}{2}[/latex]

69. [latex]sin t[/latex] = 0, [latex]cos t[/latex] = −1

71. [latex]sin t[/latex] = −0.596, [latex]cos t[/latex] = 0.803

73. [latex]sin t[/latex] = [latex]\frac{1}{2}[/latex], [latex]cos t[/latex] = [latex]\frac{\sqrt{3}}{2}[/latex]

75. [latex]sin t[/latex] = −[latex]\frac{1}{2}[/latex], [latex]cos t[/latex] = [latex]\frac{\sqrt{3}}{2}[/latex]

77. [latex]sin t[/latex] = 0.761, [latex]cos t[/latex] = −0.649

79. [latex]sin t[/latex] = 1, [latex]cos t[/latex] = 0

81. [latex]\frac{\sqrt{2}}{4}[/latex]

83. −[latex]\frac{\sqrt{6}}{4}[/latex]

85. [latex]\frac{\sqrt{2}}{4}[/latex]

87. [latex]\frac{\sqrt{2}}{4}[/latex]

89. 0

91. (0, –1)

93. 37.5 seconds, 97.5 seconds, 157.5 seconds, 217.5 seconds, 277.5 seconds, 337.5 seconds

Section 2.3 – The Other Trigonometric Functions

1. Yes, when the reference angle is [latex]\frac{π}{4}[/latex] and the terminal side of the angle is in quadrants I and III. Thus, at [latex]x[/latex] = [latex]\frac{π}{4}[/latex], [latex]\frac{5π}{4}[/latex], the sine and cosine values are equal.

3. Substitute the sine of the angle in for [latex]y[/latex] in the Pythagorean Theorem [latex]x^2[/latex] + [latex]y^2[/latex] = [latex]1[/latex]. Solve for [latex]x[/latex] and take the negative solution.

5. The outputs of tangent and cotangent will repeat every [latex]π[/latex] units.

7. [latex]\frac{2\sqrt{3}}{3}[/latex]

9. [latex]\sqrt{3}[/latex]

11. [latex]\sqrt{2}[/latex]

13. 1

15. 2

17. [latex]\frac{\sqrt{3}}{3}[/latex]

19. −[latex]\frac{2\sqrt{3}}{3}[/latex]

21. [latex]\sqrt{3}[/latex]

23. −[latex]\sqrt{2}[/latex]

25. −1

27. −2

29. −[latex]\frac{\sqrt{3}}{3}[/latex]

31. 2

33. [latex]\frac{\sqrt{3}}{3}[/latex]

35. −2

37. −1

39. If [latex]sin t[/latex] = −[latex]\frac{2\sqrt{2}}{3}[/latex], [latex]sec t[/latex] = −3, [latex]csc t[/latex] = −[latex]\frac{3\sqrt{2}}{4}[/latex], [latex]tan t[/latex] = [latex]2\sqrt{2}[/latex], [latex]cot t[/latex] = [latex]\frac{\sqrt{2}}{4}[/latex]

41. [latex]sec t[/latex] = 2, [latex]csc t[/latex] = [latex]\frac{2\sqrt{3}}{3}[/latex], [latex]tan t[/latex] = [latex]\sqrt{3}[/latex], [latex]cot t[/latex] = [latex]\frac{\sqrt{3}}{3}[/latex]

43. −[latex]\frac{\sqrt{2}}{2}[/latex]

45. 3.1

47. 1.4

49. [latex]sin t[/latex] = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]cos t[/latex] = [latex]\frac{\sqrt{2}}{2}[/latex], [latex]tan t[/latex] = 1, [latex]cot t[/latex] = 1, [latex]sec t[/latex] = [latex]\sqrt{2}[/latex], [latex]csc t[/latex] = [latex]\sqrt{2}[/latex]

51. [latex]sin t[/latex] = −[latex]\frac{\sqrt{3}}{2}[/latex], [latex]cos t[/latex] = −[latex]\frac{1}{2}[/latex], [latex]tan t[/latex] = [latex]\sqrt{3}[/latex], [latex]cot t[/latex] = [latex]\frac{\sqrt{3}}{3}[/latex], [latex]sec t[/latex] = −2, [latex]csc t[/latex] = −[latex]\frac{2\sqrt{3}}{3}[/latex]

53. [latex]sin t[/latex] ≈ 0.79

55. [latex]csc t[/latex] ≈ 1.16 

57. even

59. even

61. [latex]\frac{sin t}{cos t}[/latex]  = [latex]tan t[/latex]

63. 13.77 hours, period: [latex]1000π[/latex]

65. 7.73 inches

Section 2.4 – Right Triangle Trigonometry

1.

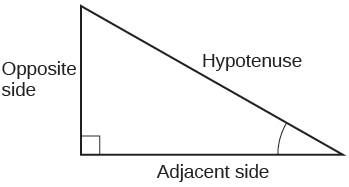
3. The tangent of an angle is the ratio of the opposite side to the adjacent side.

5. For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.

7. [latex]\frac{π}{6}[/latex]

9. [latex]\frac{π}{4}[/latex]

11. [latex]b[/latex] = [latex]\frac{20\sqrt{3}}{3}[/latex], [latex]c[/latex] = [latex]\frac{40\sqrt{3}}{3}[/latex]

13. [latex]a[/latex] = 10,000, [latex]c[/latex] = 10,000.5

15. [latex]b[/latex] = [latex]\frac{5\sqrt{3}}{3}[/latex], [latex]c[/latex] = [latex]\frac{10\sqrt{3}}{3}[/latex]

17. [latex]\frac{5\sqrt{29}}{29}[/latex]

19. [latex]\frac{5}{2}[/latex]

21. [latex]\frac{\sqrt{29}}{2}[/latex]

23. [latex]\frac{5\sqrt{41}}{41}[/latex]

25. [latex]\frac{5}{4}[/latex]

27. [latex]\frac{\sqrt{41}}{4}[/latex]

29. [latex]c[/latex] = 14, [latex]b[/latex] = 73

31. [latex]a[/latex] = 15, [latex]b[/latex] = 15

33. 188.3159

35. 200.6737

37. 498.3471 ft

39. 1060.09 ft

41. 27.372 ft

43. 22.6506 ft

45. 368.7633 ft