Section 3.4 – Inverse Trigonometric Functions
Learning Objectives
Welcome to Section 3.4! In this section, you will…
- Understand and use the inverse sine, cosine, and tangent functions.
- Find the exact value of expressions involving the inverse sine, cosine, and tangent functions.
- Find exact values of composite functions with inverse trigonometric functions.
For any right triangle, given one other angle and the length of one side, we can figure out what the other angles and sides are. But what if we are given only two sides of a right triangle? We need a procedure that leads us from a ratio of sides to an angle. This is where the notion of an inverse to a trigonometric function comes into play. In this section, we will explore the inverse trigonometric functions.
Understanding and Using the Inverse Sine, Cosine, and Tangent Functions
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure 1.

For example, if [latex]f(x)=sin x[/latex], then we would write [latex]f^{−1}(x)=sin^{−1}(x)[/latex]. Be aware that [latex]sin^{−1}(x)[/latex] does not mean [latex]\frac{1}{sinx}[/latex]. The following examples illustrate the inverse trigonometric functions:
- Since [latex]sin\frac{π}{6}=\frac{1}{2}[/latex], then [latex]\frac{π}{6}=sin^{−1}(\frac{1}{2}[/latex].
- Since [latex]cosπ=−1[/latex], then [latex]π=cos^{−1}(−1)[/latex].
- Since [latex]tan\frac{π}{4}=1[/latex], then [latex]\frac{π}{4}=tan^{−1}(1)[/latex].
In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function, if [latex]f(a)=b[/latex], then an inverse function would satisfy [latex]f^{−1}(b)=a[/latex].
Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. Figure 2 shows the graph of the sine function limited to [latex][-\frac{π}{2},\frac{π}{2}][/latex] and the graph of the cosine function limited to [latex][0,π][/latex]
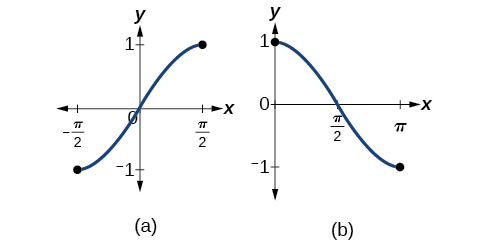
Figure 3 shows the graph of the tangent function limited to [latex](−\frac{π}{2},\frac{π}{2})[/latex].
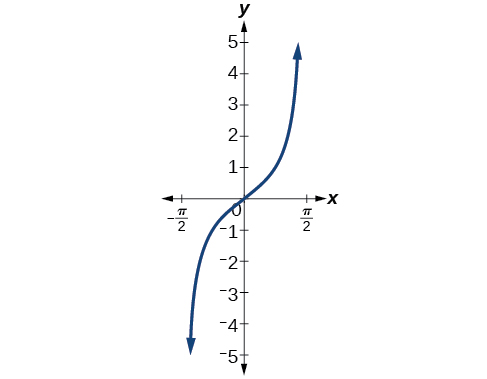
These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.
On these restricted domains, we can define the inverse trigonometric functions.
- The inverse sine function [latex]y=sin^{-1}x[/latex] means [latex]x=sin y[/latex]. The arcsine function, and notated [latex]arcsinx[/latex].
[latex]y=sin^{−1}(x)[/latex] has domain [latex][−1,1][/latex] and range [latex]−\frac{π}{2},\frac{π}{2}[/latex]
- The inverse cosine function [latex]y=cos^{-1}x[/latex] means [latex]x=cos y[/latex]. The arccosine function, and notated [latex]arccos x[/latex].
[latex]y=cos^{−1}(x)[/latex] has domain [latex][−1,1][/latex] and range [latex][0,π][/latex]
- The inverse tangent function [latex]y=tan^{-1}x[/latex] means [latex]x=tan y[/latex]. The arctangent function, and notated [latex]arctan x[/latex].
[latex]y=tan^{−1}(x)[/latex] has domain [latex](−∞,∞)[/latex] and range [latex]−\frac{π}{2},\frac{π}{2}[/latex]
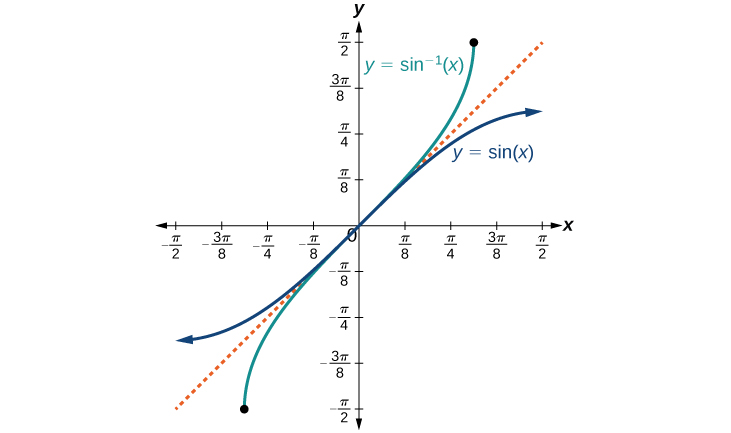
The graphs of the inverse functions are shown in Figure 4, Figure 5, and Figure 6. Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that [latex]sin^{−1}(x)[/latex] has domain [latex][−1,1][/latex] and range [latex][−\frac{π}{2},\frac{π}{2}][/latex], [latex]cos^{−1}(x)[/latex] has domain [latex][−1,1][/latex] and range [latex][0,π][/latex], and [latex]tan^{−1}(x)[/latex] has domain of all real numbers and range [latex](−\frac{π}{2},\frac{π}{2})[/latex]. To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line [latex]y=x[/latex].
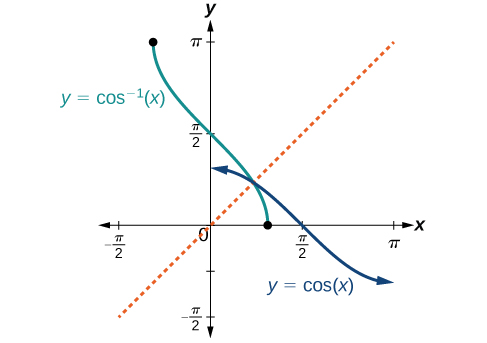
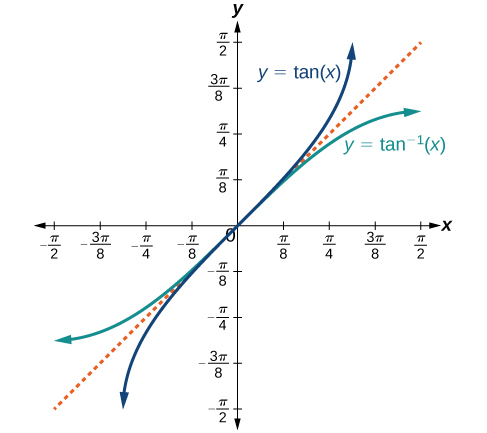
Relations for Inverse Sine, Cosine, and Tangent Functions
For angles in the interval [latex][−\frac{π}{2},\frac{π}{2}][/latex], if [latex]sin y=x[/latex], then [latex]sin^{−1}(x)=y[/latex].
For angles in the interval [latex][0,π][/latex], if [latex]cos y=x[/latex], then [latex]cos^{−1}(x)=y[/latex].
For angles in the interval [latex](−\frac{π}{2},\frac{π}{2})[/latex], if [latex]tan y=x[/latex], then [latex]tan^{−1}(x)=y[/latex].
Example 1
Writing a Relation for an Inverse Function
Given [latex]sin(\frac{5π}{12})≈0.96593[/latex], write a relation involving the inverse sine.
Show/Hide Solution
Use the relation for the inverse sine. If [latex]sin y=x[/latex], then [latex]sin^{−1}(x)=y[/latex] .
In this problem, [latex]x=0.96593[/latex], and [latex]y=\frac{5π}{12}[/latex].
[latex]sin^{−1}(0.96593)≈\frac{5π}{12}[/latex]
Try It #1
Given [latex]cos(0.5)≈0.8776[/latex], write a relation involving the inverse cosine.
Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions
Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically [latex]\frac{π}{6}[/latex] (30°), [latex]\frac{π}{4}[/latex] (45°), and [latex]\frac{π}{3}[/latex] (60°), and their reflections into other quadrants.
How To
Given a “special” input value, evaluate an inverse trigonometric function.
- Find angle [latex]x[/latex] for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
- If [latex]x[/latex] is not in the defined range of the inverse, find another angle [latex]y[/latex] that is in the defined range and has the same sine, cosine, or tangent as [latex]x[/latex], depending on which corresponds to the given inverse function.
Example 2
Evaluating Inverse Trigonometric Functions for Special Input Values
Evaluate each of the following.
ⓐ [latex]sin^{−1}(\frac{1}{2})[/latex]
ⓑ [latex]sin^{−1}(-\frac{\sqrt{2}}{2})[/latex]
ⓒ [latex]cos^{−1}(-\frac{\sqrt{3}}{2})[/latex]
ⓓ [latex]tan^{−1}(1)[/latex]
Show/Hide Solution
ⓐ Evaluating [latex]sin^{−1}(\frac{1}{2})[/latex] is the same as determining the angle that would have a sine value of [latex]\frac{1}{2}[/latex]. In other words, what angle [latex]x[/latex] would satisfy [latex]sin(x)=\frac{1}{2}[/latex]? There are multiple values that would satisfy this relationship, such as [latex]\frac{π}{6}[/latex] and [latex]\frac{5π}{6}[/latex], but we know we need the angle in the interval [latex][−\frac{π}{2},\frac{π}{2}][/latex], so the answer will be [latex]sin^{−1}(\frac{1}{2})=\frac{π}{6}[/latex]. Remember that the inverse is a function, so for each input, we will get exactly one output.
ⓑ To evaluate [latex]sin^{−1}(−\frac{\sqrt{2}}{2})[/latex], we know that [latex]\frac{5π}{4}[/latex] and [latex]\frac{7π}{4}[/latex] both have a sine value of [latex]\frac{\sqrt{−2}}{2}[/latex], but neither is in the interval [latex][−\frac{π}{2},\frac{π}{2}][/latex]. For that, we need the negative angle coterminal with [latex]\frac{7π}{4}: [latex]sin^{−1}(−\frac{\sqrt{2}}{2})=−\frac{π}{4}[/latex].
ⓒTo evaluate [latex]cos^{−1}(−\frac{\sqrt{3}}{2})[/latex], we are looking for an angle in the interval [latex][0,π][/latex] with a cosine value of [latex]−\frac{\sqrt{3}}{2}[/latex]. The angle that satisfies this is [latex]cos^{−1}(−\frac{\sqrt{3}}{2})=\frac{5π}{6}[/latex].
ⓓ Evaluating [latex]tan^{−1}(1)[/latex], we are looking for an angle in the interval [latex](−\frac{π}{2},\frac{π}{2})[/latex] with a tangent value of 1. The correct angle is [latex]tan^{−1}(1)=\frac{π}{4}[/latex].
Try It #2
Evaluate each of the following.
ⓐ [latex]sin^{−1}(−1)[/latex]
ⓑ [latex]tan^{−1}(−1)[/latex]
ⓒ [latex]cos^{−1}(−1)[/latex]
ⓓ [latex]cos^{−1}(\frac{1}{2})[/latex]
How To
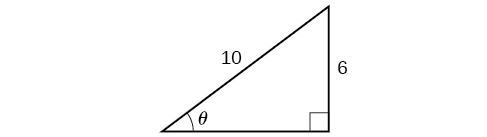
Given two sides of a right triangle like the one shown in Figure 7, find an angle.
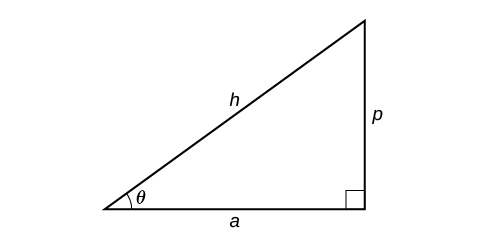
- If one given side is the hypotenuse of length [latex]h[/latex] and the side of length [latex]a[/latex] adjacent to the desired angle is given, use the equation [latex]θ=cos^{−1}(\frac{a}{h})[/latex].
- If one given side is the hypotenuse of length [latex]h[/latex] and the side of length [latex]p[/latex] opposite to the desired angle is given, use the equation [latex]θ=sin^{−1}(\frac{p}{h})[/latex].
- If the two legs (the sides adjacent to the right angle) are given, then use the equation [latex]θ=tan^{−1}(\frac{p}{a})[/latex].
Example 3
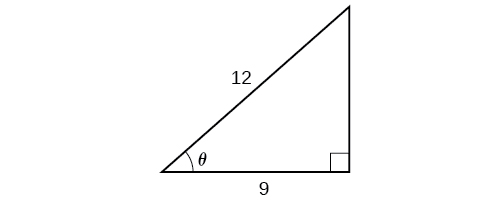
Applying the Inverse Cosine to a Right Triangle
Solve the triangle in Figure 8 for the angle [latex]θ[/latex].
Show/Hide Solution
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.

Finding Exact Values of Composite Functions with Inverse Trigonometric Functions
There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let [latex]f(x)[/latex] and [latex]g(x)[/latex] be two different trigonometric functions belonging to the set [latex]\{sin(x),cos(x),tan(x)\}[/latex] and let [latex]f^{−1}(y)[/latex] and [latex]g^{−1}(y)[/latex] be their inverses.
Evaluating Compositions of the Form [latex]f(f^{−1}(y))[/latex] and [latex]f^{-1}(f(x))[/latex]
For any trigonometric function, [latex]f(f^{−1}(y))=y[/latex] for all [latex]y[/latex] in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of [latex]f[/latex] was defined to be identical to the domain of [latex]f^{−1}[/latex]. However, we have to be a little more careful with expressions of the form [latex]f^{−1}(f(x))[/latex].
Compositions of a trigonometric function and its inverse
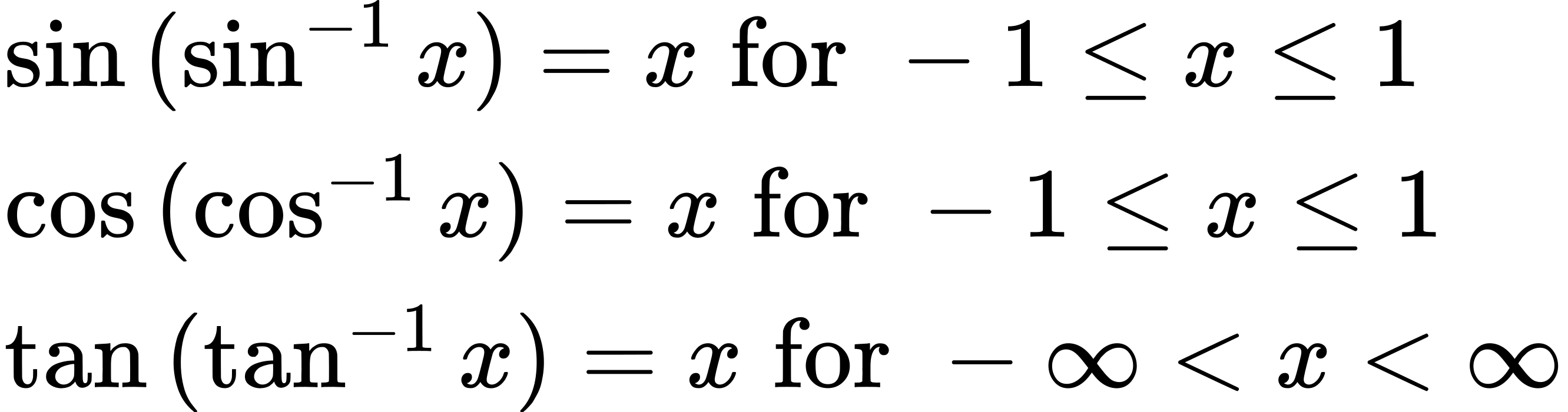
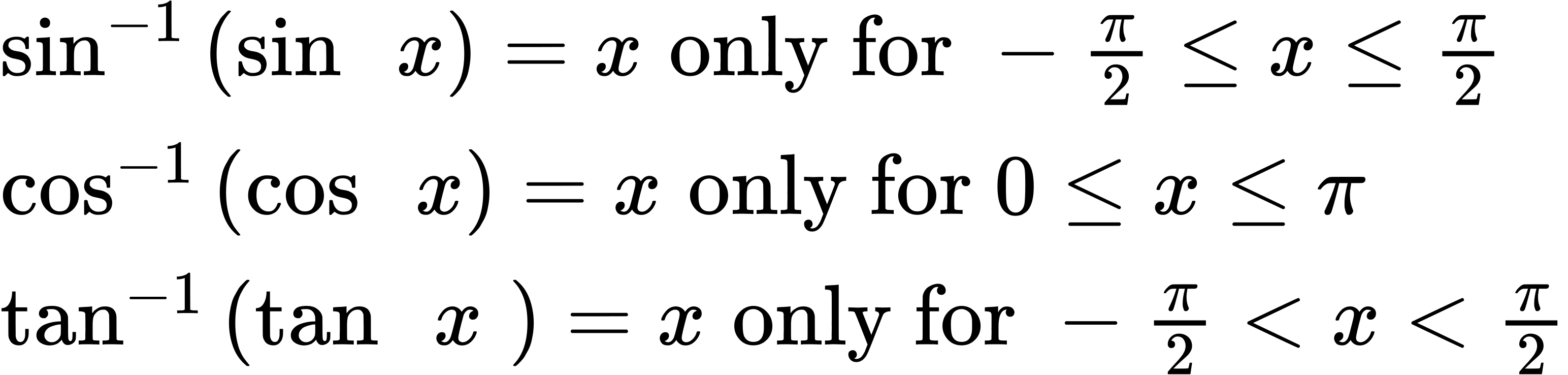
Q&A
Is it correct that [latex]sin^{−1}(sin x)=x?[/latex]
No. This equation is correct if [latex]x[/latex] belongs to the restricted domain [latex]−\frac{π}{2},\frac{π}{2}[/latex], but sine is defined for all real input values, and for [latex]x[/latex] outside the restricted interval, the equation is not correct because its inverse always returns a value in [latex]−\frac{π}{2},\frac{π}{2}[/latex]. The situation is similar for cosine and tangent and their inverses. For example, [latex]sin^{−1}(sin\frac{3π}{4})=\frac{π}{4}[/latex].
How To
Given an expression of the form f−1(f(θ)) where [latex]f(θ)=sin θ[/latex], [latex]cos θ[/latex], or [latex]tan θ[/latex], evaluate.
- If [latex]θ[/latex] is in the restricted domain of [latex]f[/latex], then [latex]f^{−1}(f(θ))=θ[/latex].
- If not, then find an angle [latex]ϕ[/latex] within the restricted domain of [latex]f[/latex] such that [latex]f(ϕ)=f(θ)[/latex]. Then [latex]f^{−1}(f(θ))=ϕ[/latex].
Example 4
Using Inverse Trigonometric Functions
Evaluate the following:
ⓐ [latex]sin^{−1}(sin(\frac{π}{3}))[/latex]
ⓑ [latex]sin^{−1}(sin(\frac{2π}{3}))[/latex]
ⓒ [latex]cos^{−1}(cos(\frac{2π}{3}))[/latex]
ⓓ [latex]cos^{−1}(cos(−\frac{π}{3}))[/latex]
Show/Hide Solution
ⓐ [latex]\frac{π}{3}[/latex] is in [latex][−\frac{π}{2},\frac{π}{2}][/latex], so [latex]sin^{−1}(sin(\frac{π}{3}))=\frac{π}{3}[/latex].
ⓑ [latex]\frac{2π}{3}[/latex] is not in [latex]−\frac{π}{2},\frac{π}{2}][/latex], but [latex]sin(\frac{2π}{3})=sin(\frac{π}{3})[/latex], so [latex]sin^{−1}(sin(\frac{2π}{3}))=\frac{π}{3}[/latex].
ⓒ [latex]\frac{2π}{3}[/latex] is in [latex][0,π][/latex], so [latex]cos^{−1}(cos(\frac{2π}{3}))=\frac{2π}{3}[/latex].
ⓓ [latex]−\frac{π}{3}[/latex] is not in [latex][0,π][/latex], but [latex]cos(−\frac{π}{3})=cos\frac{π}{3}[/latex] because cosine is an even function. [latex]\frac{π}{3}[/latex] is in [latex][0,π][/latex], so [latex]cos^{−1}(cos(−\frac{π}{3}))=\frac{π}{3}[/latex].
Try It #5
Evaluate [latex]tan^{−1}(tan(\frac{π}{8})) and tan^{−1}(tan(\frac{11π}{9}))[/latex].
Evaluating Compositions of the Form [latex]f^{−1}(g(x))[/latex]
Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form [latex]f^{−1}(g(x))[/latex]. For special values of [latex]x[/latex], we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is [latex]θ[/latex], making the other [latex]\frac{π}{2}−θ[/latex]. Consider the sine and cosine of each angle of the right triangle in Figure 10.
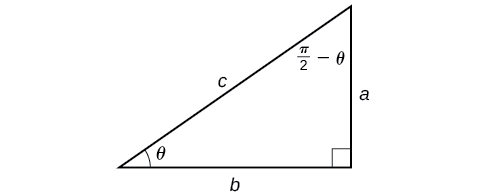
Because [latex]cos θ=\frac{b}{c}=sin(\frac{π}{2}−θ)[/latex], we have [latex]sin^{−1}(cos θ)=\frac{π}{2}−θ[/latex] if [latex]0≤θ≤π[/latex]. If [latex]θ[/latex] is not in this domain, then we need to find another angle that has the same cosine as [latex]θ[/latex] and does belong to the restricted domain; we then subtract this angle from [latex]\frac{π}{2}[/latex]. Similarly, [latex]sin θ=\frac{a}{c}=cos(\frac{π}{2}−θ)[/latex], so [latex]cos^{−1}(sin θ)=\frac{π}{2}−θ[/latex] if [latex]−\frac{π}{2}≤θ≤\frac{π}{2}[/latex]. These are just the function-cofunction relationships presented in another way.
How To
Given functions of the form [latex]sin^{−1}(cos x)[/latex] and [latex]cos^{−1}(sin x)[/latex], evaluate them.
- If [latex]x[/latex] is in [latex][0,π][/latex], then [latex]sin^{−1}(cos x=\frac{π}{2}−x[/latex].
- If x is not in [latex][0,π][/latex], then find another angle y in [latex][0,π][/latex] such that [latex]cos y=cos x[/latex].
[latex]sin^{−1}(cos x)=\frac{π}{2}−y[/latex]
- If [latex]x[/latex] is in [latex][−\frac{π}{2},\frac{π}{2}][/latex], then [latex]cos^{−1}(sin x)=\frac{π}{2}−x[/latex].
- If [latex]x[/latex] is not in [latex][−\frac{π}{2},\frac{π}{2}][/latex], then find another angle [latex]y[/latex] in [latex][−\frac{π}{2},\frac{π}{2}][/latex] such that [latex]sin y=sin x[/latex].
[latex]cos^{−1}(sin x)=\frac{π}{2}−y[/latex]
Example 5
Evaluating the Composition of an Inverse Sine with a Cosine
Evaluate [latex]sin^{−1}(cos(\frac{13π}{6}))[/latex]
ⓐby direct evaluation.
ⓑ by the method described previously.
Show/Hide Solution
ⓐ Here, we can directly evaluate the inside of the composition.
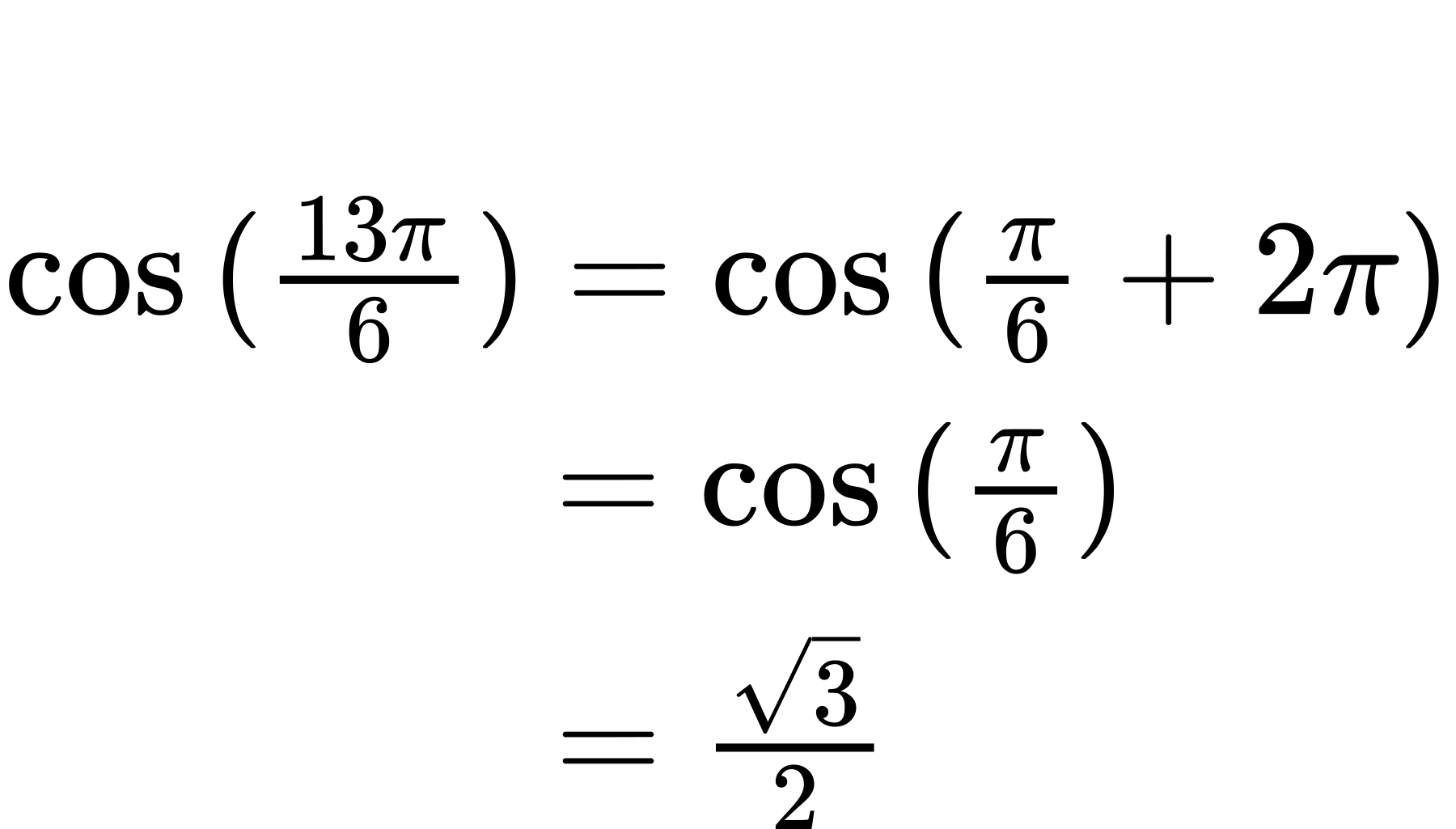
Now, we can evaluate the inverse function as we did earlier.
[latex]sin^{−1}(\frac{\sqrt{3}}{2})=\frac{π}{3}[/latex]
ⓑ We have [latex]x=\frac{13π}{6}, y=\frac{π}{6}[/latex], and
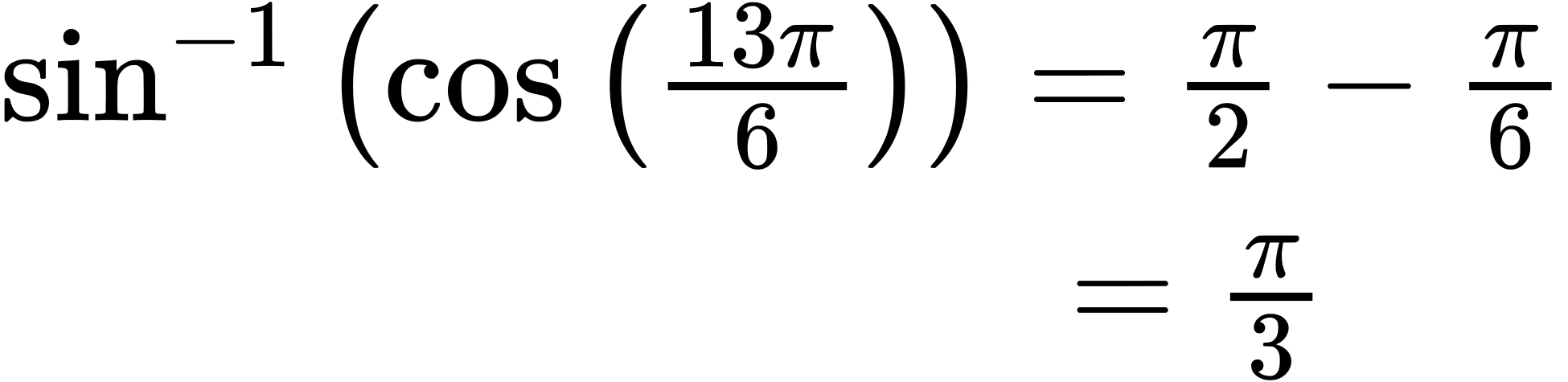
Try It #6
Evaluate [latex]cos^{−1}(sin(-\frac{11π}{4}))[/latex].
Evaluating Compositions of the Form [latex]f(g^{−1}(x))[/latex]
To evaluate compositions of the form [latex]f(g^{−1}(x))[/latex], where [latex]f[/latex] and [latex]g[/latex] are any two of the functions sine, cosine, or tangent and [latex]x[/latex] is any input in the domain of [latex]g^{−1}([/latex], we have exact formulas, such as [latex]sin(cos^{−1}(x))=\sqrt{1−x^2}[/latex]. When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, [latex]sin^2x+cos^2x=1[/latex], to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
Example 6
Evaluating the Composition of a Sine with an Inverse Cosine
Find an exact value for [latex]sin(cos^{−1}(\frac{4}{5}))[/latex].
Show/Hide Solution
Beginning with the inside, we can say there is some angle such that [latex]θ=cos^{−1}(\frac{4}{5})[/latex], which means [latex]cos θ=\frac{4}{5}[/latex], and we are looking for [latex]sin θ[/latex]. We can use the Pythagorean identity to do this.

Since [latex]θ=cos^{−1}(\frac{4}{5})[/latex] is in quadrant I, [latex]sin θ[/latex] must be positive, so the solution is [latex]\frac{3}{5}[/latex]. See Figure 11.
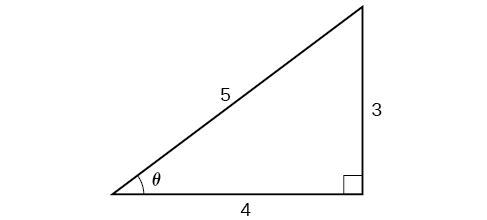
We know that the inverse cosine always gives an angle on the interval [latex][0,π][/latex], so we know that the sine of that angle must be positive; therefore [latex]sin(cos^{−1}(\frac{4}{5}))=sin θ=\frac{3}{5}[/latex].
Try It #7
Evaluate [latex]cos(tan^{−1}(\frac{5}{12}))[/latex].
Example 7
Evaluating the Composition of a Sine with an Inverse Tangent
Find an exact value for [latex]sin(tan^{−1}(\frac{7}{4}))[/latex].
Show/Hide Solution
While we could use a similar technique as in Example 5, we will demonstrate a different technique here. From the inside, we know there is an angle such that [latex]tan θ=\frac{7}{4}[/latex]. We can envision this as the opposite and adjacent sides on a right triangle, as shown in Figure 12.
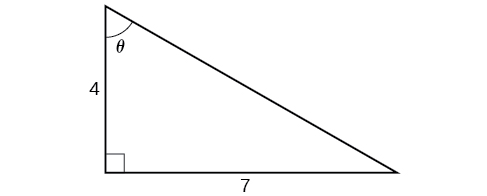
Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.
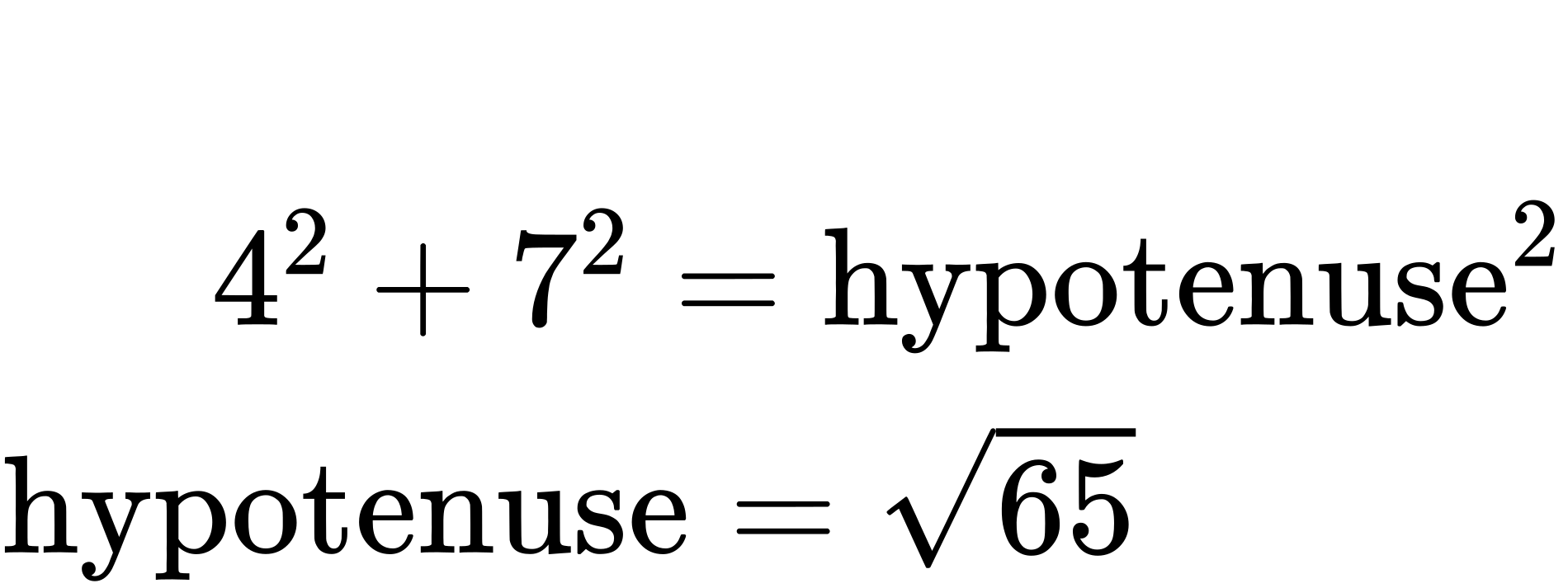
Now, we can evaluate the sine of the angle as the opposite side divided by the hypotenuse.
[latex]sin θ=765[/latex]
This gives us our desired composition.
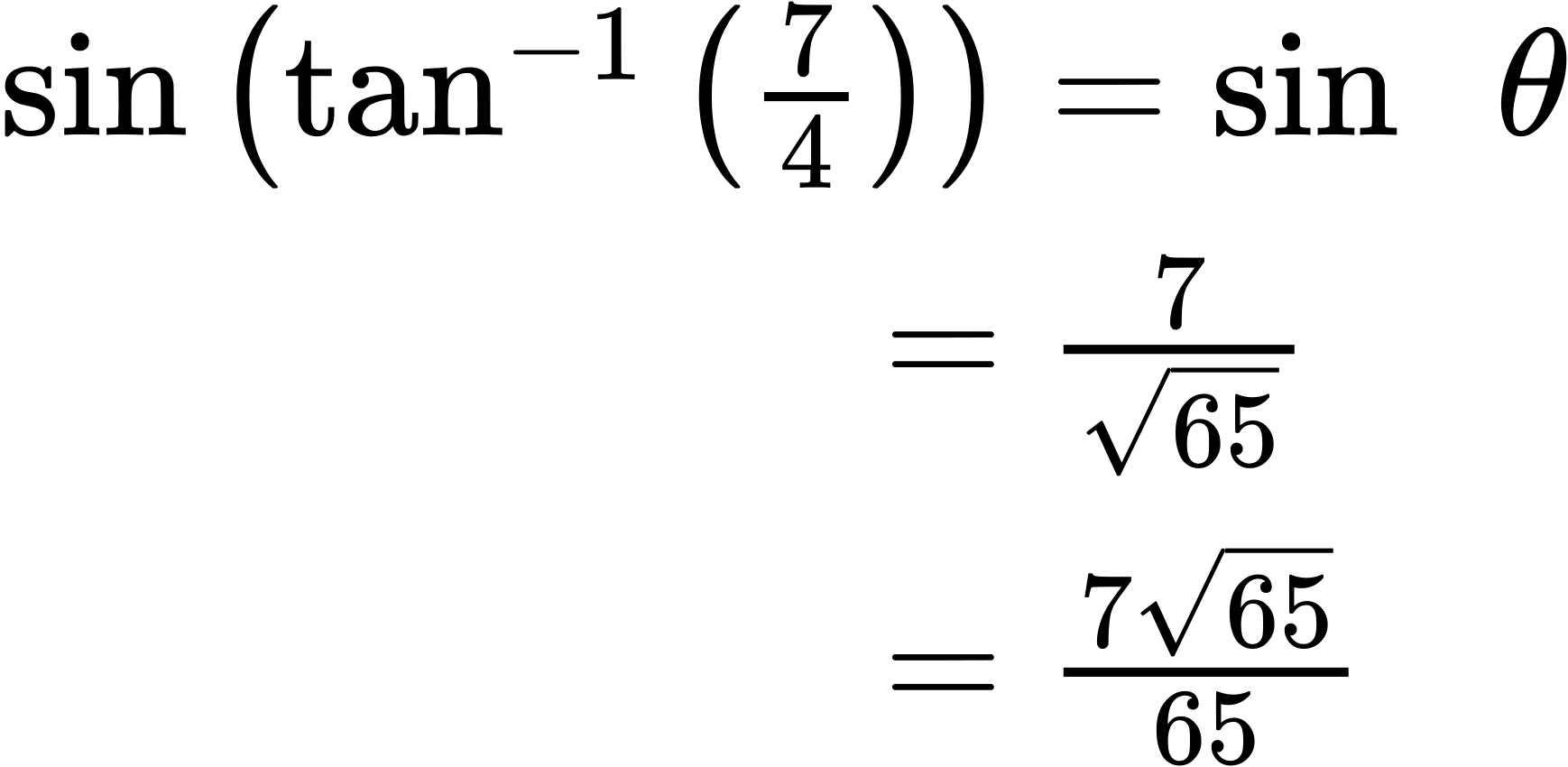
Try It #8
Evaluate [latex]cos(sin^{−1}(\frac{7}{9}))[/latex].
Example 8
Finding the Cosine of the Inverse Sine of an Algebraic Expression
Find a simplified expression for [latex]cos(sin^{−1}(\frac{x}{3}))[/latex] for [latex]−3≤x≤3[/latex].
Show/Hide Solution
We know there is an angle [latex]θ[/latex] such that [latex]sin θ=\frac{x}{3}[/latex].
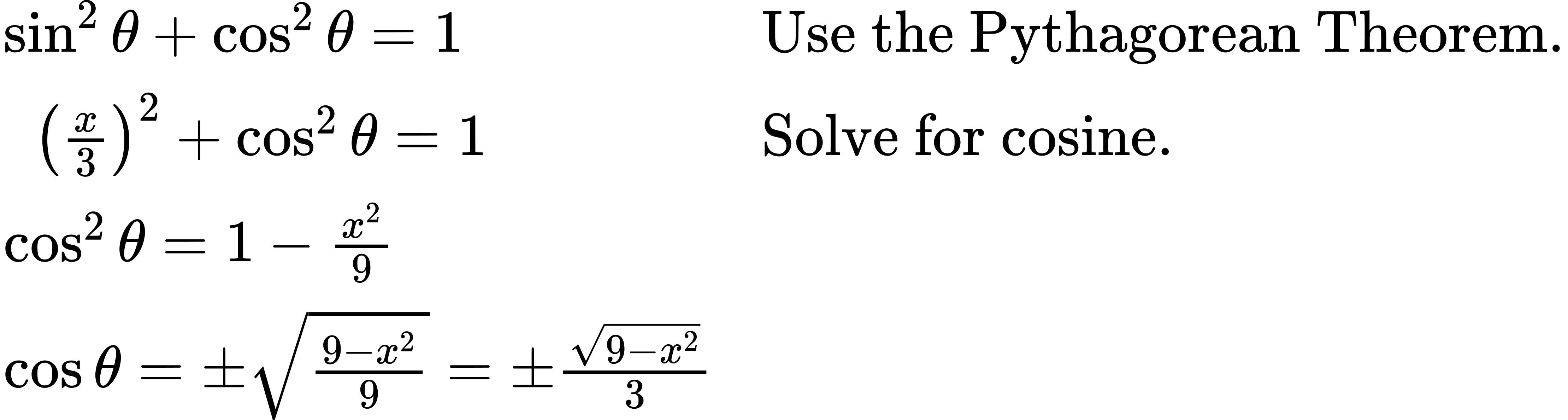
Because we know that the inverse sine must give an angle on the interval [latex][−\frac{π}{2},\frac{π}{2}][/latex], we can deduce that the cosine of that angle must be positive.
[latex]cos(sin^{−1}(\frac{x}{3}))=\frac{\sqrt{9−x^2}}{3}[/latex]
Try It #9
Find a simplified expression for [latex]sin(tan^{−1}(4x))[/latex] for [latex]−14≤x≤14[/latex].
Media
Access this online resource for additional instruction and practice with inverse trigonometric functions.
3.4 Section Exercises
Verbal
1. Why do the functions [latex]f(x)=sin^{−1}(x)[/latex] and [latex]g(x)=cos^{−1}(x)[/latex] have different ranges?
2. Since the functions [latex]y=cos x[/latex] and [latex]y=cos^{−1}(x)[/latex] are inverse functions, why is [latex]cos^{−1}(cos(−\frac{π}{6}))[/latex] not equal to [latex]−\frac{π}{6}[/latex]?
3. Explain the meaning of [latex]\frac{π}{6}=arcsin0.5[/latex].
4. Most calculators do not have a key to evaluate [latex]sec^{−1}(2)[/latex]. Explain how this can be done using the cosine function or the inverse cosine function.
5. Why must the domain of the sine function, [latex]sin x[/latex], be restricted to [latex][−\frac{π}{2},\frac{π}{2}][/latex] for the inverse sine function to exist?
6. Discuss why this statement is incorrect: [latex]arccos(cos x)=x[/latex] for all [latex]x[/latex].
7. Determine whether the following statement is true or false and explain your answer: [latex]arccos(−x)=π−arccos x[/latex].
Algebraic
For the following exercises, evaluate the expressions.
8. [latex]sin^{−1}(\frac{\sqrt{2}}{2})[/latex]
9. [latex]sin^{−1}(-\frac{1}{2})[/latex]
10. [latex]cos^{−1}(\frac{1}{2})[/latex]
11. [latex]cos^{−1}(−\frac{\sqrt{2}}{2})[/latex]
12. [latex]tan^{−1}(1)[/latex]
13. [latex]tan^{−1}(−\sqrt{3})[/latex]
14. [latex]tan^{−1}(−1)[/latex]
15. [latex]tan^{−1}(\sqrt{3})[/latex]
16. [latex]tan^{−1}(\frac{−1}{\sqrt{3}})[/latex]
For the following exercises, use a calculator to evaluate each expression. Express answers to the nearest hundredth.
17. [latex]cos^{−1}(−0.4)[/latex]
18. [latex]arcsin(0.23)[/latex]
19. [latex]arccos(\frac{3}{5})[/latex]
20. [latex]cos^{−1}(0.8)[/latex]
21. [latex]tan^{−1}(6)[/latex]
For the following exercises, find the angle [latex]θ[/latex] in the given right triangle. Round answers to the nearest hundredth.
22.
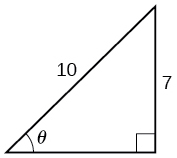
23.
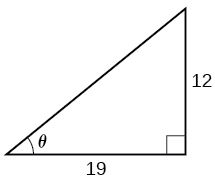
For the following exercises, find the exact value, if possible, without a calculator. If it is not possible, explain why.
24. [latex]sin^{−1}(cos(π))[/latex]
25. [latex]tan^{−1}(sin(π))[/latex]
26. [latex]cos^{−1}(sin(\frac{π}{3}))[/latex]
27. [latex]tan^{−1}(sin(\frac{π}{3}))[/latex]
28. [latex]sin^{−1}(cos(\frac{-π}{2}))[/latex]
29. [latex]tan^{−1}(sin(\frac{4π}{3}))[/latex]
30. [latex]sin^{−1}(sin(\frac{5π}{6}))[/latex]
31. [latex]tan^{−1}(sin(−\frac{5π}{2}))[/latex]
32. [latex]cos(sin^{−1}(\frac{4}{5}))[/latex]
33. [latex]sin(cos^{−1}(\frac{3}{5}))[/latex]
34. [latex]sin(tan^{−1}(\frac{4}{3}))[/latex]
35. [latex]cos(tan^{−1}(\frac{12}{5}))[/latex]
36. [latex]cos(sin^{−1}(\frac{1}{2}))[/latex]
For the following exercises, find the exact value of the expression in terms of [latex]x[/latex] with the help of a reference triangle.
37. [latex]tan(sin^{−1}(x−1))[/latex]
38. [latex]sin(cos^{−1}(1−x))[/latex]
39. [latex]cos(sin^{−1}(\frac{1}{x}))[/latex]
40. [latex]cos(tan^{−1}(3x−1))[/latex]
41. [latex]tan(sin^{−1}(x+\frac{1}{2}))[/latex]
Extensions
For the following exercises, evaluate the expression without using a calculator. Give the exact value.
42.
[latex]\frac{sin^{−1}(\frac{1}{2})−cos^{−1}(\frac{\sqrt{2}}{2})+sin^{−1}(\frac{\sqrt{3}}{2})−cos^{−1}(1)}{cos^{−1}(\frac{\sqrt{3}}{2})−sin^{−1}(\frac{\sqrt{2}}{2})+cos^{−1}(\frac{1}{2})−sin^{−1}(0)}[/latex]
For the following exercises, find the function if [latex]sin t=\frac{x}{x+1}[/latex].
43. [latex]cos t[/latex]
44. [latex]sec t[/latex]
45. [latex]cot t[/latex]
46. [latex]cos(sin^{−1}(\frac{x}{x+1}))[/latex]
47. [latex]tan^{−1}(\frac{x}{\sqrt{2x+1}})[/latex]
Graphical
48. Graph [latex]y=sin^{−1}(x)[/latex] and state the domain and range of the function.
49. Graph [latex]y=arccos x[/latex] and state the domain and range of the function.
50. Graph one cycle of [latex]y=tan^{−1}(x)[/latex] and state the domain and range of the function.
51. For what value of [latex]x[/latex] does [latex]sin x=sin^{−1}(x)?[/latex] Use a graphing calculator to approximate the answer.
52. For what value of [latex]x[/latex] does [latex]cos x=cos^{−1}(x)?[/latex] Use a graphing calculator to approximate the answer.
Real-World Applications
53. Suppose a 13-foot ladder is leaning against a building, reaching to the bottom of a second-floor window 12 feet above the ground. What angle, in radians, does the ladder make with the building?
54. Suppose you drive 0.6 miles on a road so that the vertical distance changes from 0 to 150 feet. What is the angle of elevation of the road?
55. An isosceles triangle has two congruent sides of length 9 inches. The remaining side has a length of 8 inches. Find the angle that a side of 9 inches makes with the 8-inch side.
56. Without using a calculator, approximate the value of [latex]arctan(10,000)[/latex]. Explain why your answer is reasonable.
57. A truss (interior beam structure) for the roof of a house is constructed from two identical right triangles. Each has a base of 12 feet and height of 4 feet. Find the measure of the acute angle adjacent to the 4-foot side.
58. The line [latex]y=\frac{3}{5}x[/latex] passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the positive x-axis?
59. The line [latex]y=\frac{−3}{7}x[/latex] passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the negative x-axis?
60. What percentage grade should a road have if the angle of elevation of the road is 4 degrees? (The percentage grade is defined as the change in the altitude of the road over a 100-foot horizontal distance. For example a 5% grade means that the road rises 5 feet for every 100 feet of horizontal distance.)
61. A 20-foot ladder leans up against the side of a building so that the foot of the ladder is 10 feet from the base of the building. If specifications call for the ladder's angle of elevation to be between 35 and 45 degrees, does the placement of this ladder satisfy safety specifications?
62. Suppose a 15-foot ladder leans against the side of a house so that the angle of elevation of the ladder is 42 degrees. How far is the foot of the ladder from the side of the house?