Section 4.2 – Sum and Difference Identities
Learning Objectives
Welcome to Section 4.2! In this section you will…
- Use sum and difference formulas for cosine.
- Use sum and difference formulas for sine.
- Use sum and difference formulas for tangent.
- Use sum and difference formulas for cofunctions.
- Use sum and difference formulas to verify identities.

How can the height of a mountain be measured? What about the distance from Earth to the sun? Like many seemingly impossible problems, we rely on mathematical formulas to find the answers. The trigonometric identities, commonly used in mathematical proofs, have had real-world applications for centuries, including their use in calculating long distances.
The trigonometric identities we will examine in this section can be traced to Al-Khwarizmi, a Persian astronomer who lived around 950 AD, but the ancient Greeks discovered these same formulas much earlier and stated them in terms of chords. These are special equations or postulates, true for all values input to the equations, and with innumerable applications.
In this section, we will learn techniques that will enable us to solve problems such as the ones presented above. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity.
Using the Sum and Difference Formulas for Cosine
Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. We can use the special angles, which we can review in the unit circle shown in Figure 2.
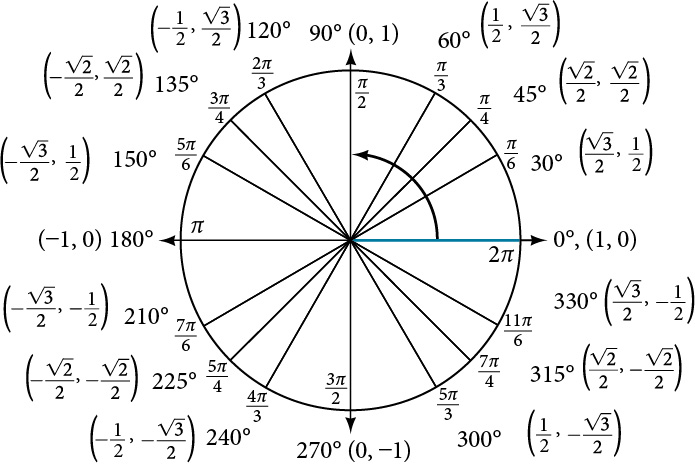
We will begin with the sum and difference formulas for cosine, so that we can find the cosine of a given angle if we can break it up into the sum or difference of two of the special angles. See Table 1.
|
Sum formula for cosine |
[latex]cos[/latex] ([latex]α[/latex] + [latex]β[/latex]) = [latex]cos α[/latex] [latex]cos β[/latex] − [latex]sin α[/latex] [latex]sin β[/latex]
|
|
Difference formula for cosine |
[latex]cos[/latex] ([latex]α[/latex] − [latex]β[/latex]) = [latex]cos α[/latex] [latex]cos β[/latex] + [latex]sin α[/latex] [latex]sin β[/latex]
|
First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle. See Figure 3. Point [latex]P[/latex] is at an angle [latex]α[/latex] from the positive x-axis with coordinates ([latex]cos α[/latex], [latex]sin α[/latex]) and point [latex]Q[/latex] is at an angle of [latex]β[/latex] from the positive x-axis with coordinates ([latex]cos β[/latex], [latex]sin β[/latex]). Note the measure of angle [latex]POQ[/latex] is [latex]α[/latex] − [latex]β[/latex].
Label two more points: [latex]A[/latex] at an angle of [latex]α[/latex] − [latex]β[/latex] from the positive x-axis with coordinates ([latex]cos[/latex] ([latex]α[/latex] − [latex]β[/latex]), [latex]sin[/latex] ([latex]α[/latex] − [latex]β[/latex])); and point [latex]B[/latex] with coordinates [latex](1, 0)[/latex]. Triangle [latex]POQ[/latex] is a rotation of triangle [latex]AOB[/latex] and thus the distance from [latex]P[/latex] to [latex]Q[/latex] is the same as the distance from [latex]A[/latex] to [latex]B[/latex].
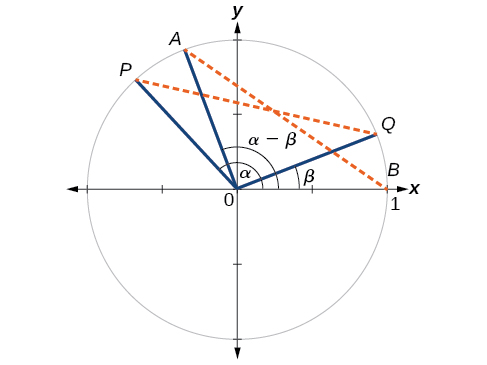
We can find the distance from [latex]P[/latex] to [latex]Q[/latex] using the distance formula.
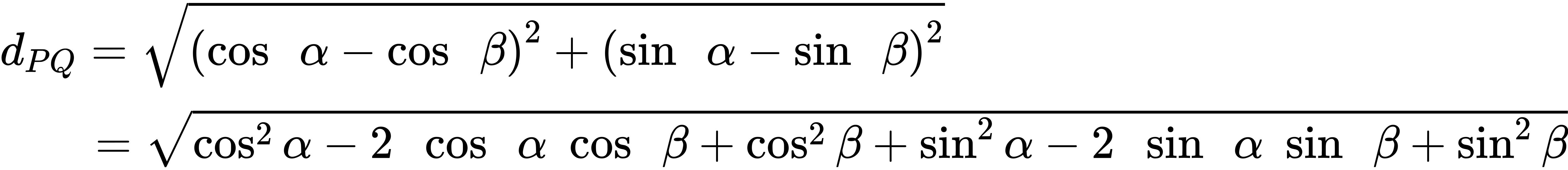
Then we apply the Pythagorean Identity and simplify.
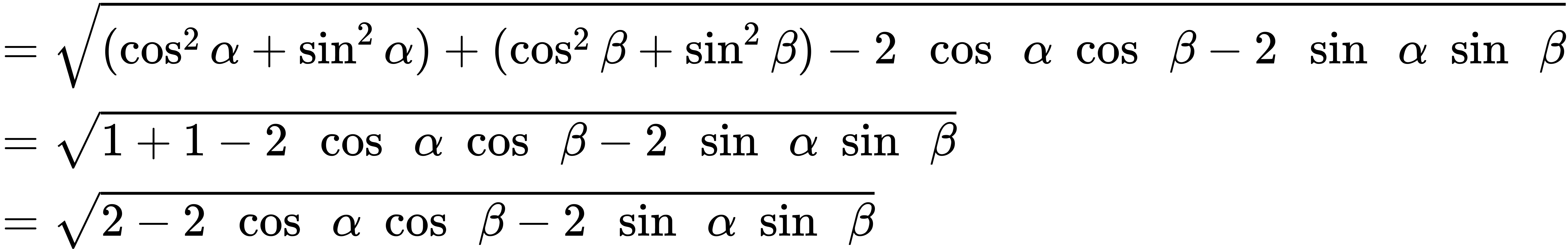
Similarly, using the distance formula we can find the distance from [latex]A[/latex] to [latex]B[/latex].
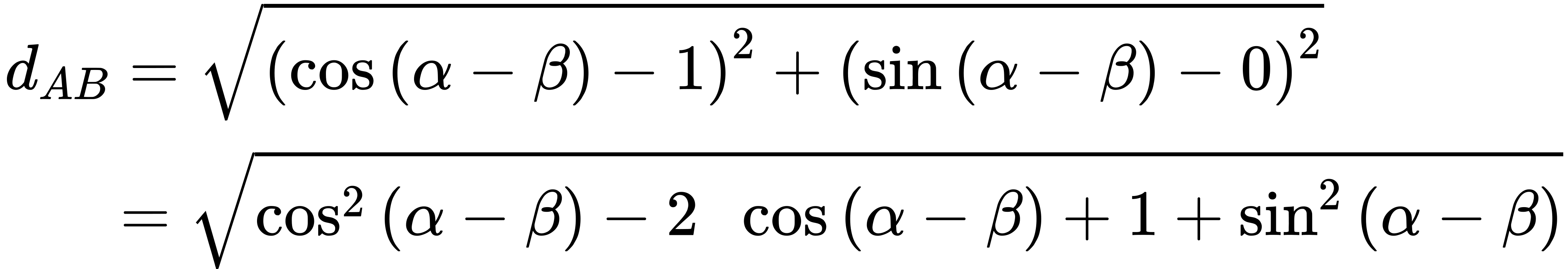
Applying the Pythagorean Identity and simplifying we get:
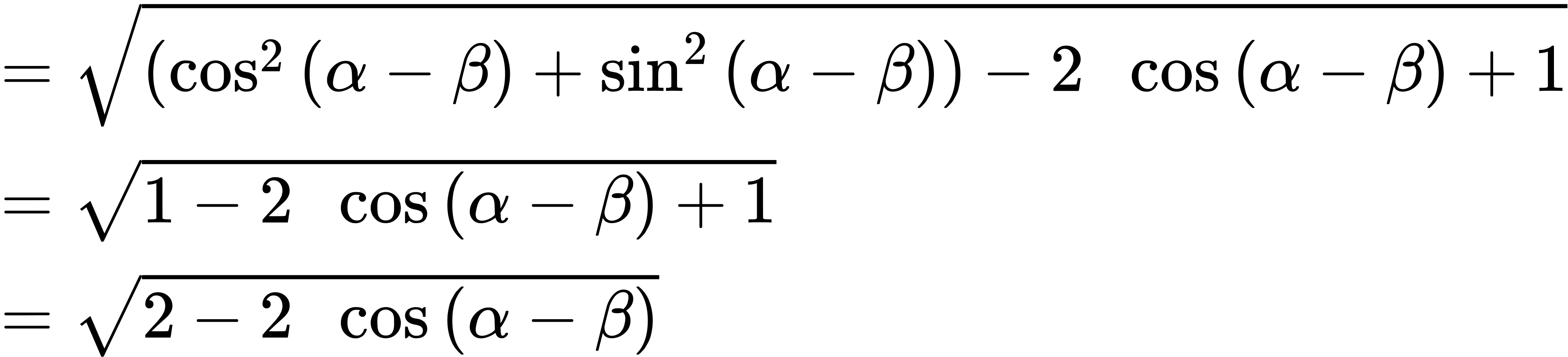
Because the two distances are the same, we set them equal to each other and simplify.
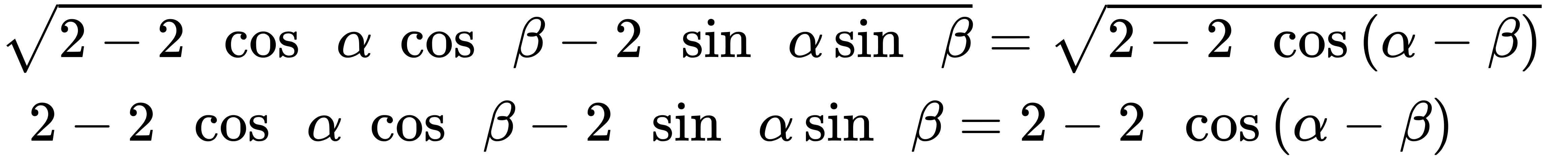
Finally we subtract 2 from both sides and divide both sides by −2.
Thus, we have the difference formula for cosine. We can use similar methods to derive the cosine of the sum of two angles.
Sum and Difference Formulas for Cosine
These formulas can be used to calculate the cosine of sums and differences of angles.
How To
Given two angles, find the cosine of the difference between the angles.
- Write the difference formula for cosine.
- Substitute the values of the given angles into the formula.
- Simplify.
Example 1
Find the Exact Value Using the Formula for the Cosine of the Difference of Two Angles
Use the cosine of the difference of angles formula to find the exact value of [latex]cos[/latex] ([latex]\frac{5π}{4}[/latex] − [latex]\frac{π}{6}[/latex]).
Show/Hide Solution
Solution
Use the formula for the cosine of the difference of two angles. We have
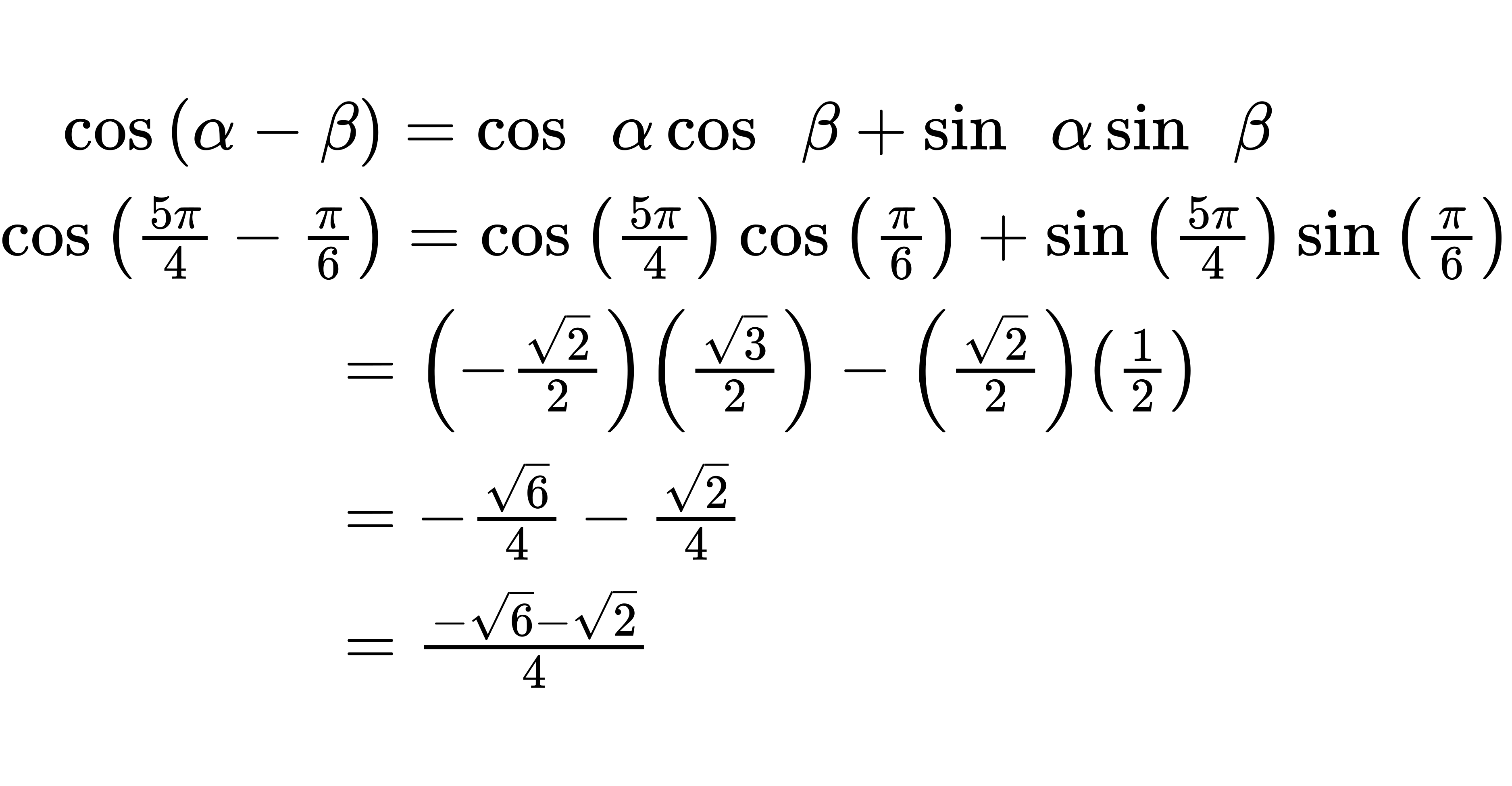
Try It #1
Find the exact value of [latex]cos[/latex] ([latex]\frac{π}{3}[/latex] − [latex]\frac{π}{4}[/latex]).
Example 2
Finding the Exact Value Using the Formula for the Sum of Two Angles for Cosine
Find the exact value of [latex]cos[/latex] (75°).
Show/Hide Solution
Solution
As 75° = 45° + 30°, we can evaluate [latex]cos[/latex] (75°) as [latex]cos[/latex] (45° + 30°). Thus,
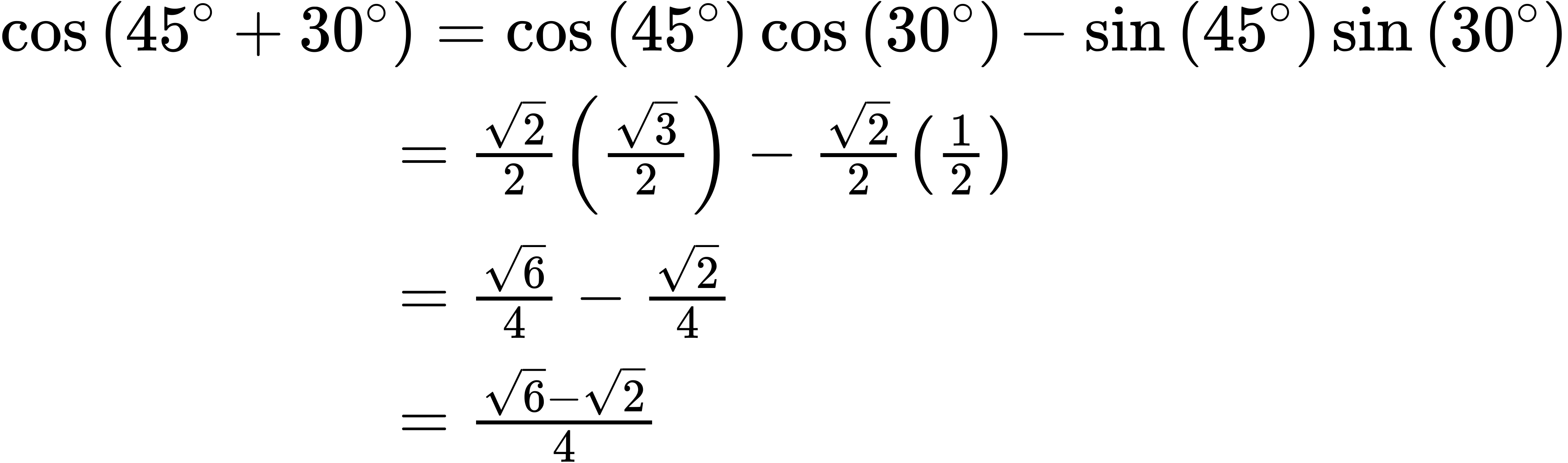
Try It #2
Find the exact value of [latex]cos[/latex] (105°).
Using the Sum and Difference Formulas for Sine
The sum and difference formulas for sine can be derived in the same manner as those for cosine, and they resemble the cosine formulas.
Sum and Difference Formulas for Sine
These formulas can be used to calculate the sines of sums and differences of angles.
How To
Given two angles, find the sine of the difference between the angles.
- Write the difference formula for sine.
- Substitute the given angles into the formula.
- Simplify.
Example 3
Using Sum and Difference Identities to Evaluate the Difference of Angles
Use the sum and difference identities to evaluate the difference of the angles and show that part a equals part b.
ⓐ [latex]sin[/latex] (45° − 30°)
ⓑ [latex]sin[/latex] (135° − 120°)
Show/Hide Solution
Solution
ⓐ Let’s begin by writing the formula and substitute the given angles.
![]()
Next, we need to find the values of the trigonometric expressions.
Now we can substitute these values into the equation and simplify.
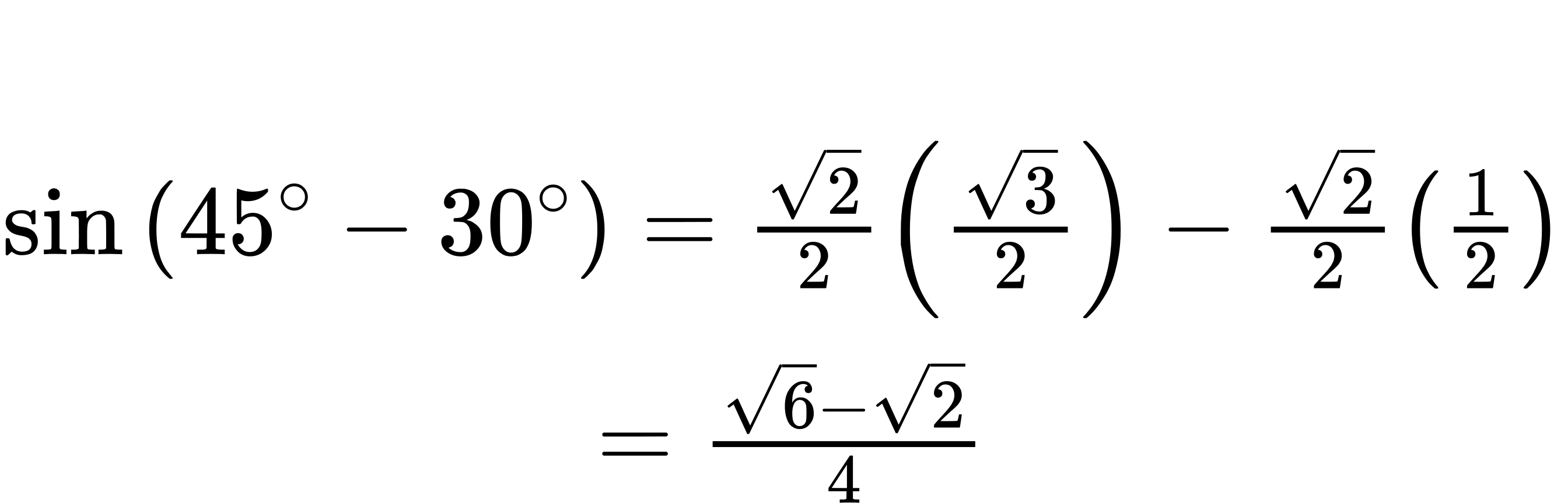
ⓑ Again, we write the formula and substitute the given angles.
![]()
Next, we find the values of the trigonometric expressions.
Now we can substitute these values into the equation and simplify.
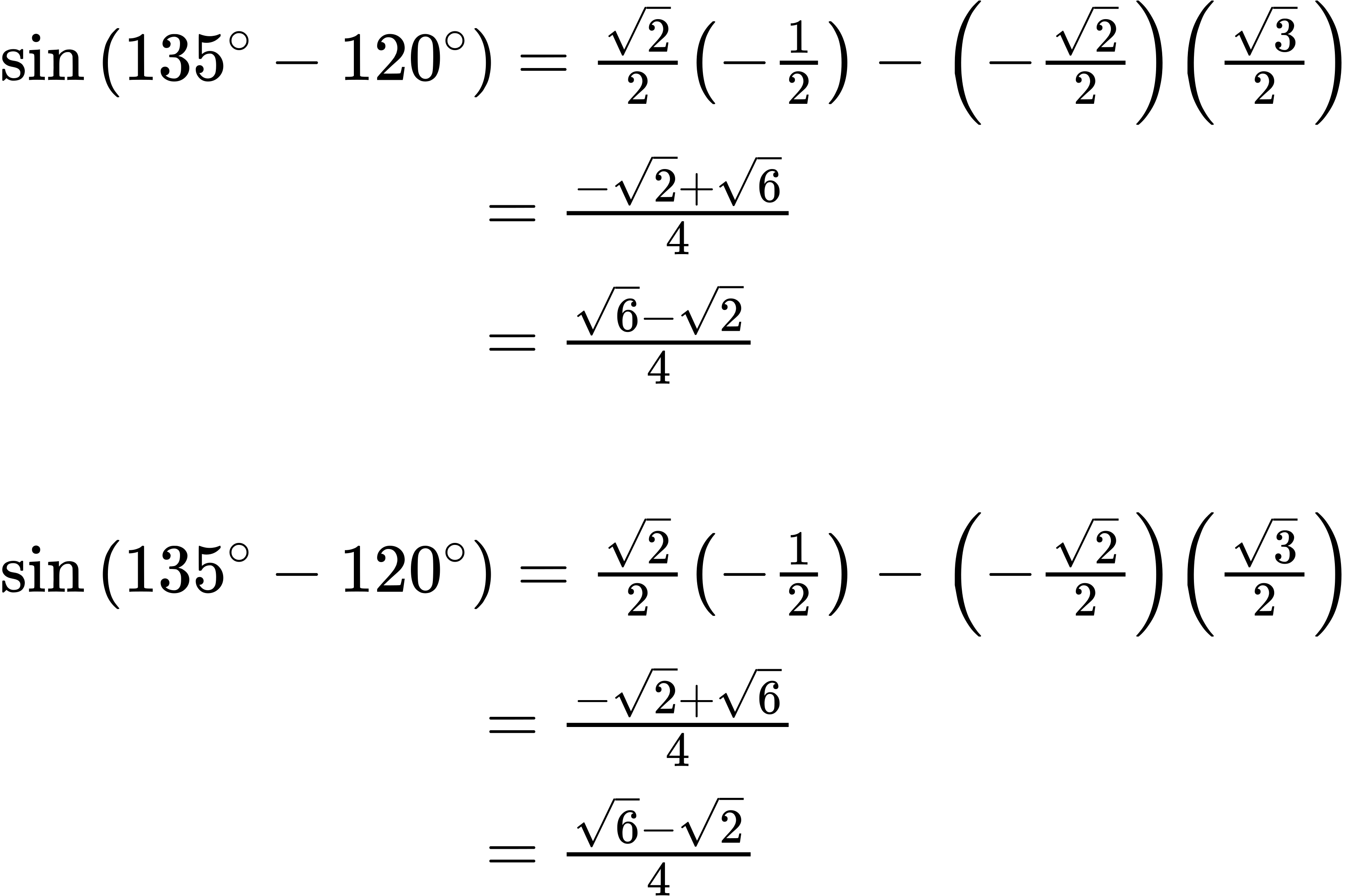
Example 4
Finding the Exact Value of an Expression Involving an Inverse Trigonometric Function
Find the exact value of [latex]sin[/latex] ([latex]cos^{−1}[/latex] [latex]\frac{1}{2}[/latex] + [latex]sin^{−1}[/latex] [latex]\frac{3}{5}[/latex]).
Show/Hide Solution
Solution
The pattern displayed in this problem is [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]). Let [latex]α[/latex] = [latex]cos^{−1}[/latex] [latex]\frac{1}{2}[/latex] and [latex]β[/latex] = [latex]sin^{−1}[/latex] [latex]\frac{3}{5}[/latex]. Then we can write
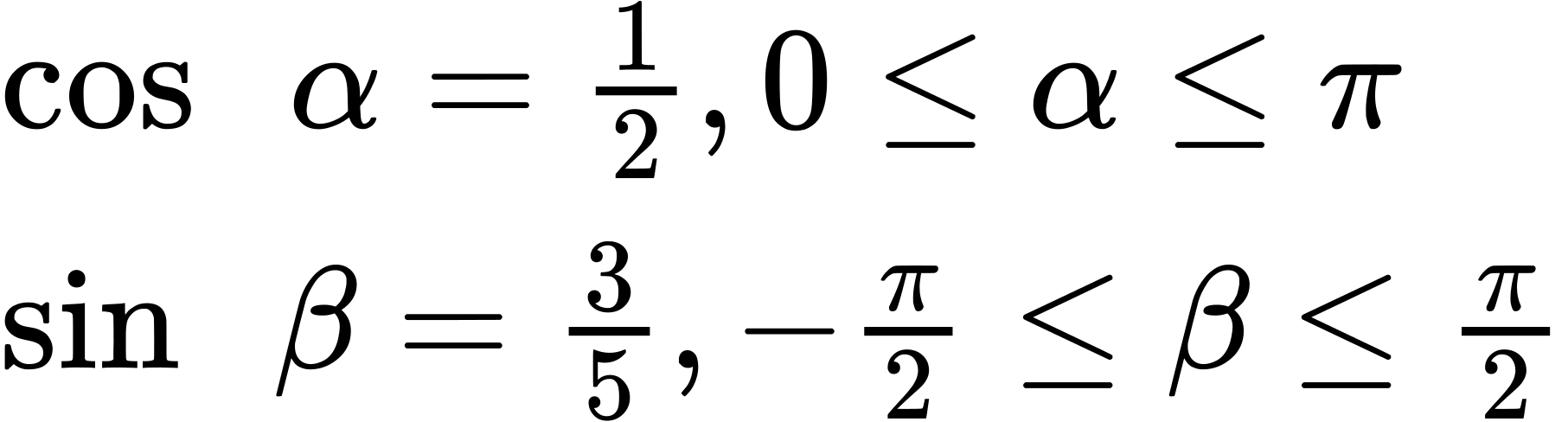
We will use the Pythagorean Identities to find [latex]sin α[/latex] and [latex]cos β[/latex].
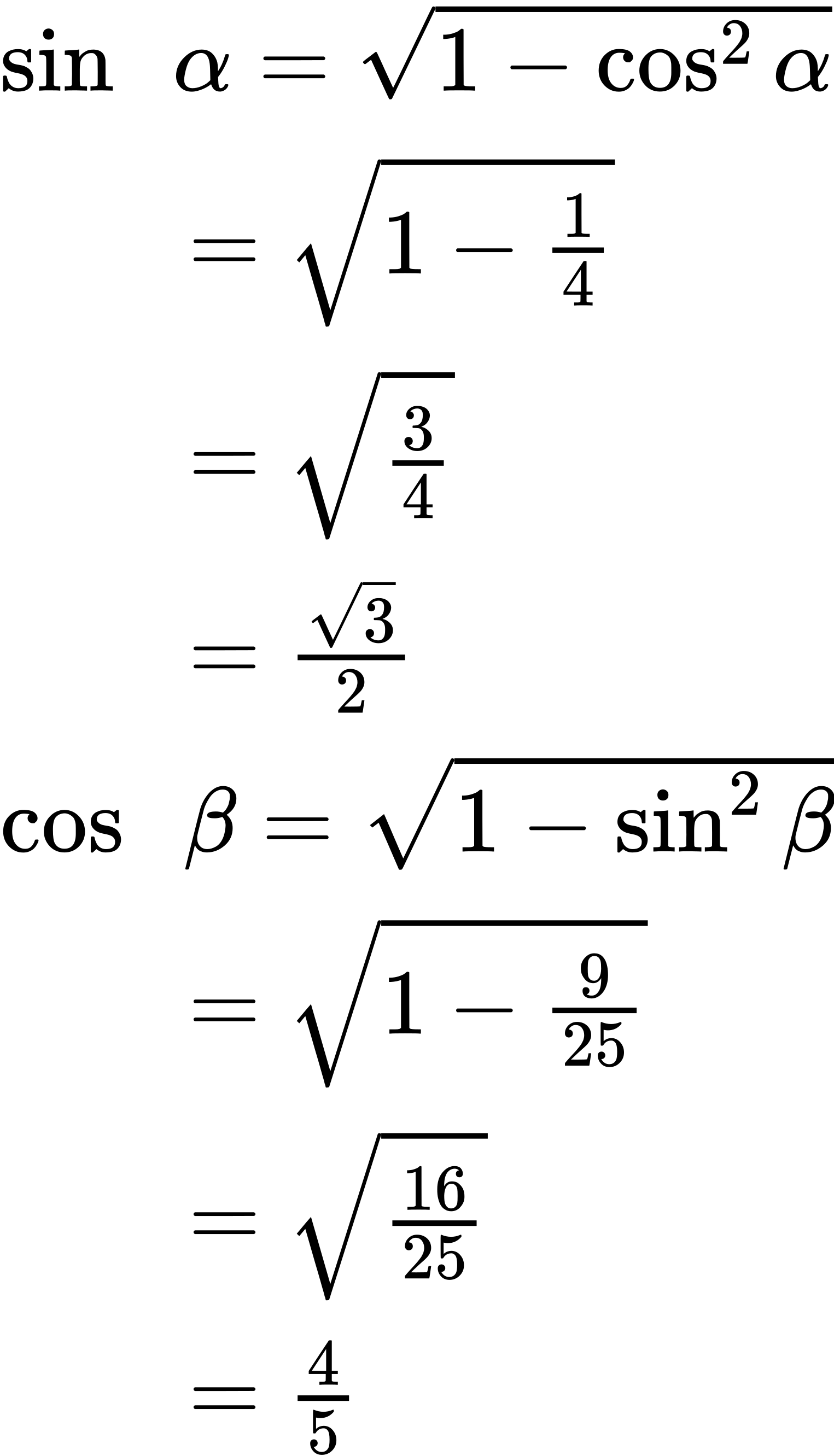
Using the sum formula for sine,
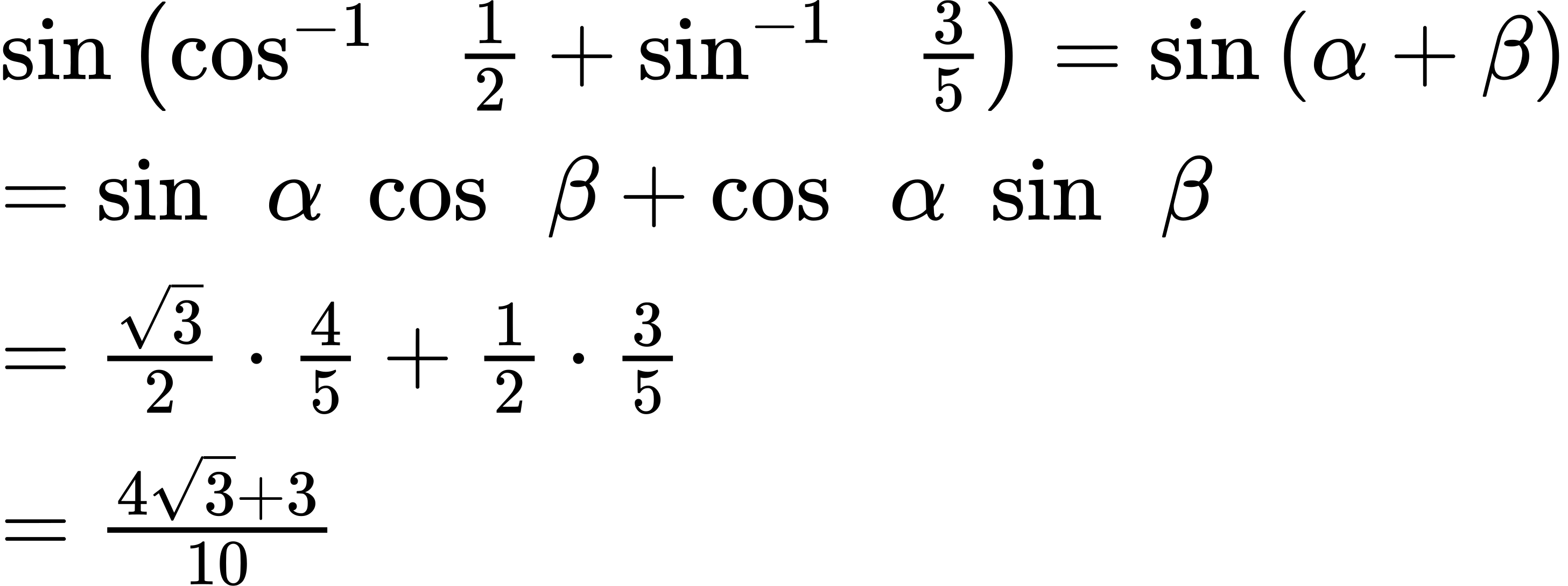
Using the Sum and Difference Formulas for Tangent
Finding exact values for the tangent of the sum or difference of two angles is a little more complicated, but again, it is a matter of recognizing the pattern.
Finding the sum of two angles formula for tangent involves taking quotient of the sum formulas for sine and cosine and simplifying. Recall, [latex]tan x[/latex] = [latex]\frac{sin x}{cos x}[/latex], [latex]cos x[/latex] ≠ 0.
Let’s derive the sum formula for tangent.

We can derive the difference formula for tangent in a similar way.
Sum and Difference Formulas for Tangent
The sum and difference formulas for tangent are:
How To
Given two angles, find the tangent of the sum of the angles.
- Write the sum formula for tangent.
- Substitute the given angles into the formula.
- Simplify.
Example 5
Finding the Exact Value of an Expression Involving Tangent
Find the exact value of [latex]tan[/latex] ([latex]\frac{π}{6}[/latex] + [latex]\frac{π}{4}[/latex]).
Show/Hide Solution
Solution
Let’s first write the sum formula for tangent and substitute the given angles into the formula.
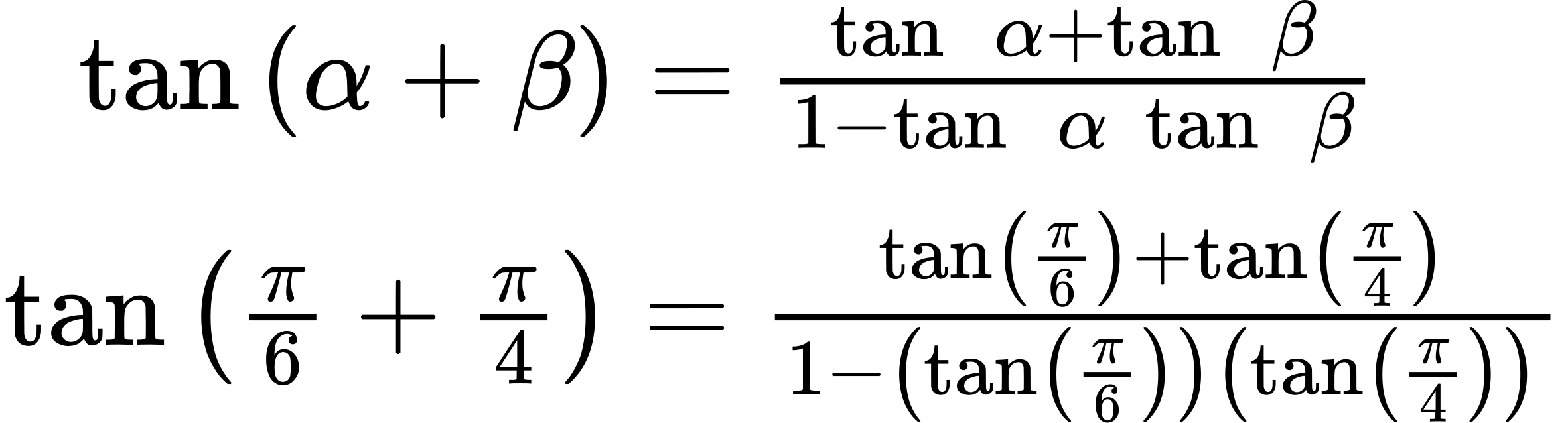
Next, we determine the individual tangents within the formula:
So we have
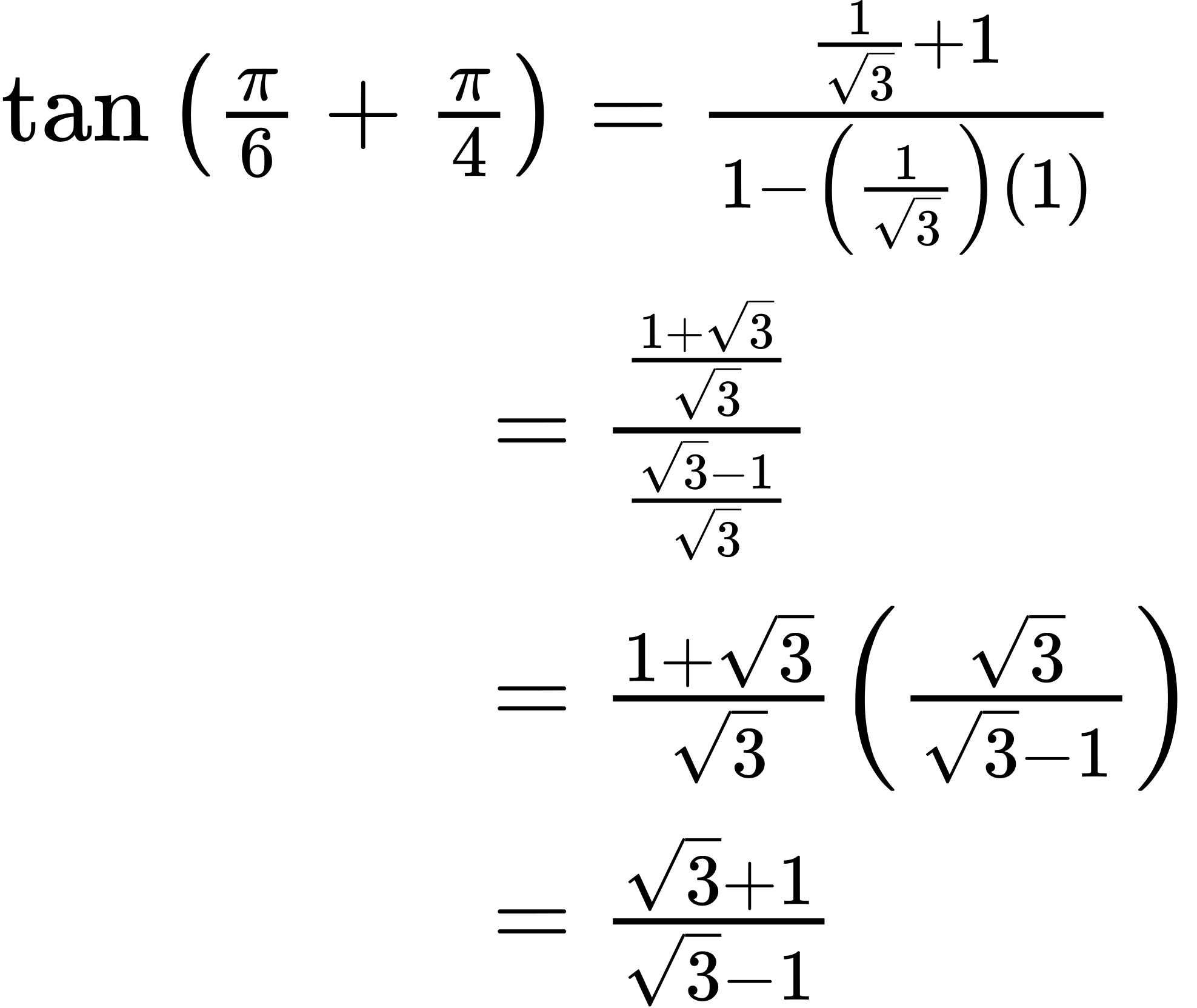
Try It #3
Find the exact value of [latex]tan[/latex] ([latex]\frac{2π}{3}[/latex] + [latex]\frac{π}{4}[/latex]).
Example 6
Finding Multiple Sums and Differences of Angles
Given [latex]sin α[/latex] = [latex]\frac{3}{5}[/latex], [latex]0[/latex] < [latex]α[/latex] < [latex]\frac{π}{2}[/latex], and [latex]cos β[/latex] = −[latex]\frac{5}{13}[/latex], [latex]π[/latex] < [latex]β[/latex] < [latex]\frac{3π}{2}[/latex], find
ⓐ [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex])
ⓑ [latex]cos[/latex] ([latex]α[/latex] + [latex]β[/latex])
ⓒ [latex]tan[/latex] ([latex]α[/latex] + [latex]β[/latex])
ⓓ [latex]tan[/latex] ([latex]α[/latex] − [latex]β[/latex])
Show/Hide Solution
Solution
We can use the sum and difference formulas to identify the sum or difference of angles when the ratio of sine, cosine, or tangent is provided for each of the individual angles. To do so, we construct what is called a reference triangle to help find each component of the sum and difference formulas.
ⓐ To find [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]), we begin with [latex]sin α[/latex] = [latex]\frac{3}{5}[/latex] and [latex]0[/latex] < [latex]α[/latex] < [latex]\frac{π}{2}[/latex]. The side opposite [latex]α[/latex] has length 3, the hypotenuse has length 5, and [latex]α[/latex] is in the first quadrant. See Figure 4. Using the Pythagorean Theorem, we can find the length of side
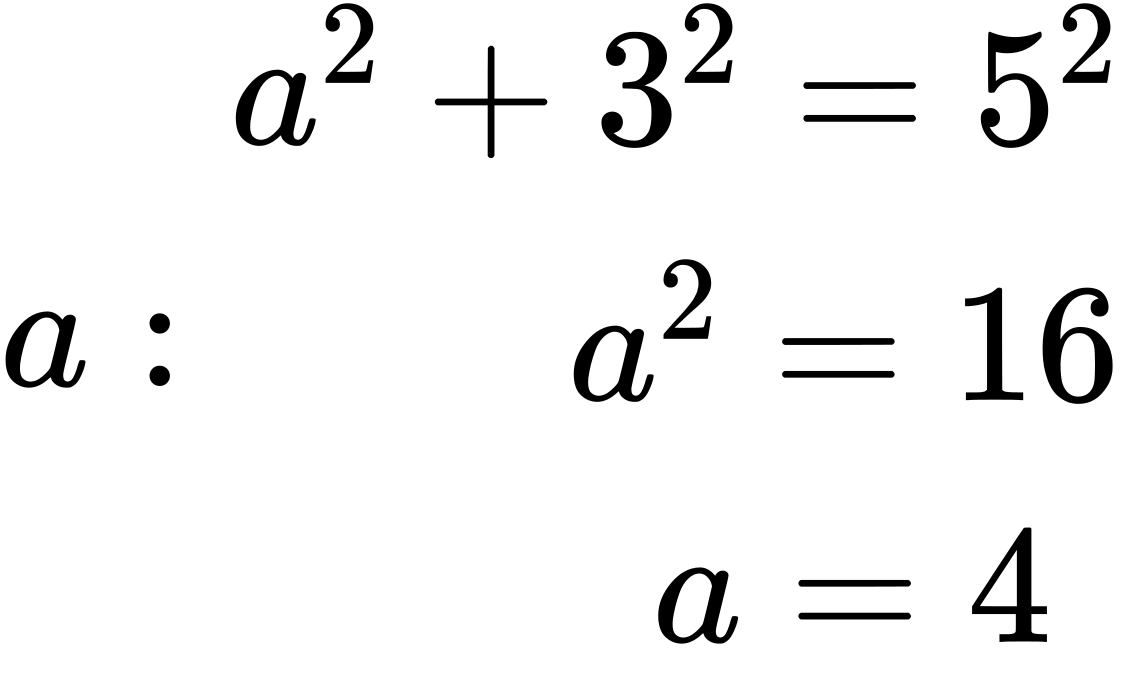

Since [latex]cos β[/latex] = −[latex]\frac{5}{13}[/latex] and [latex]π[/latex] < [latex]β[/latex] < [latex]\frac{3π}{2}[/latex], the side adjacent to [latex]β[/latex] is −5, the hypotenuse is 13, and [latex]β[/latex] is in the third quadrant. See Figure 5. Again, using the Pythagorean Theorem, we have:
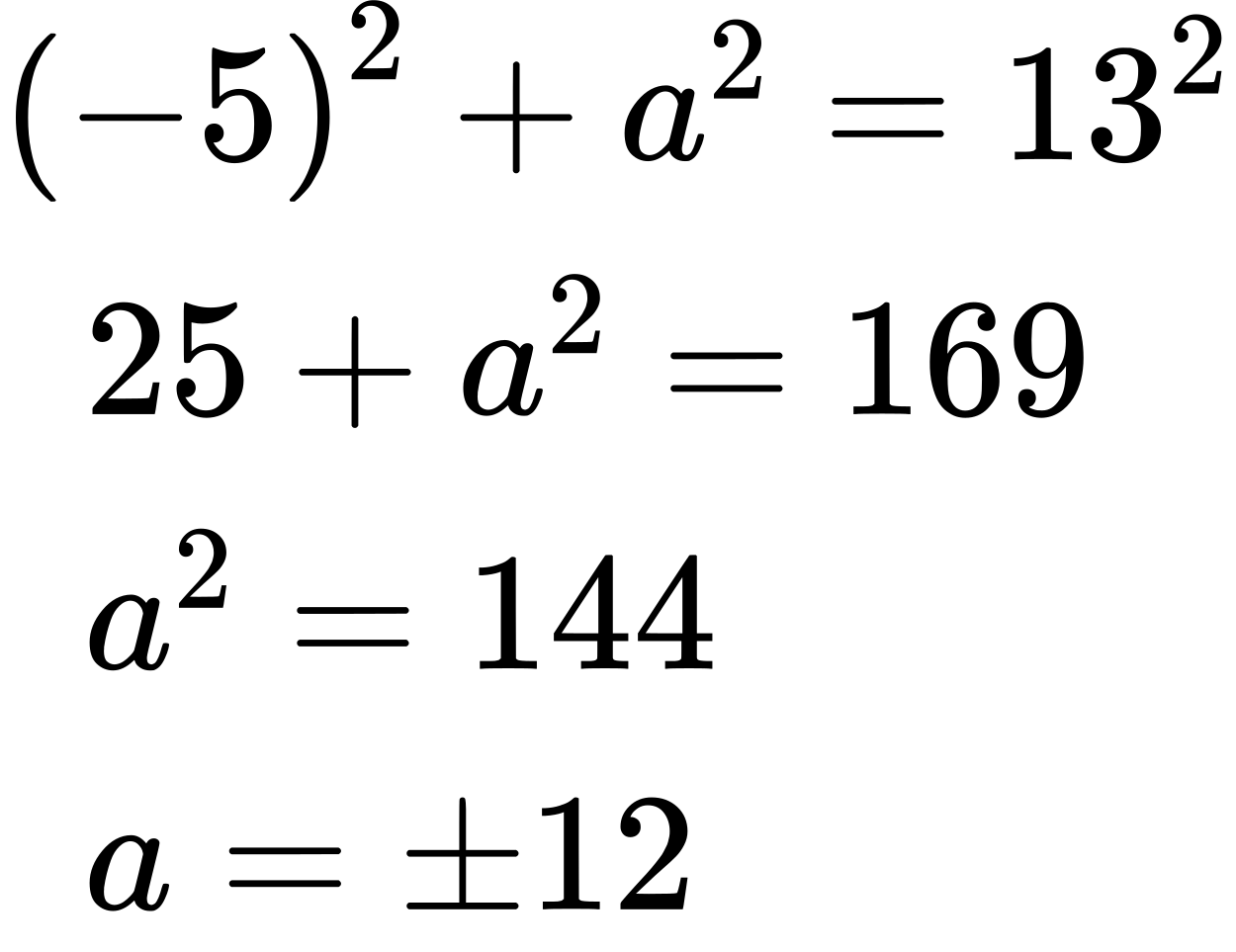
Since [latex]β[/latex] is in the third quadrant, [latex]a[/latex] = –12.

The next step is finding the cosine of [latex]α[/latex] and the sine of [latex]β[/latex]. The cosine of [latex]α[/latex] is the adjacent side over the hypotenuse. We can find it from the triangle in Figure 5: [latex]cos α[/latex] = [latex]\frac{4}{5}[/latex]. We can also find the sine of [latex]β[/latex] from the triangle in Figure 5, as opposite side over the hypotenuse: [latex]sin β[/latex] = −[latex]\frac{12}{13}[/latex]. Now we are ready to evaluate [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]).
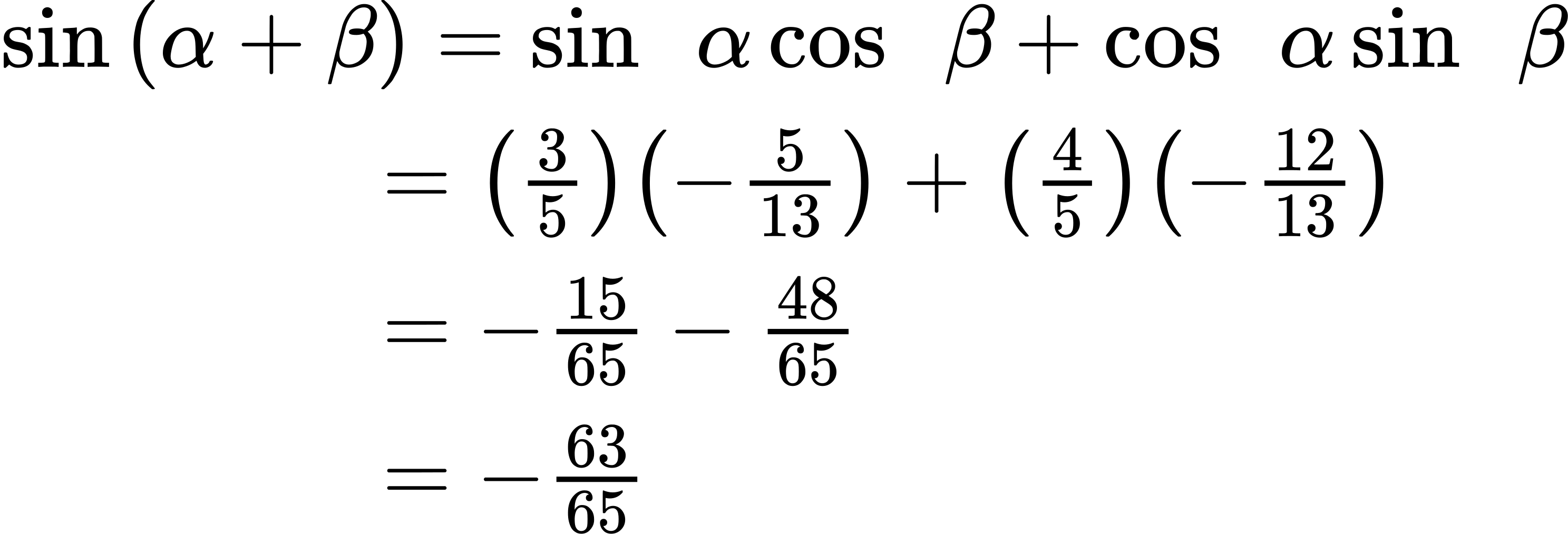
ⓑ We can find [latex]cos[/latex] ([latex]α[/latex] + [latex]β[/latex]) in a similar manner. We substitute the values according to the formula.
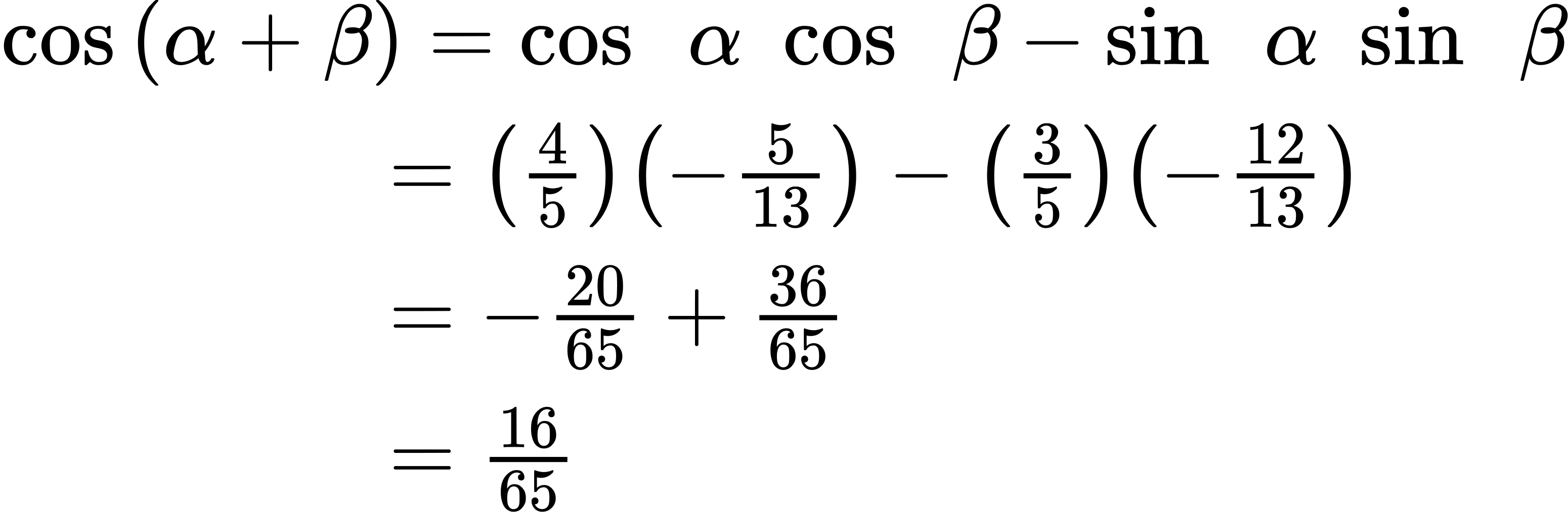
ⓒ For [latex]tan[/latex] ([latex]α[/latex] + [latex]β[/latex]), if [latex]sin α[/latex] = [latex]\frac{3}{5}[/latex] and [latex]cos α[/latex] = [latex]\frac{4}{5}[/latex], then:
If [latex]sin β[/latex] = −[latex]\frac{12}{13}[/latex] and [latex]cos β[/latex] = −[latex]\frac{5}{13}[/latex], then:
Then,
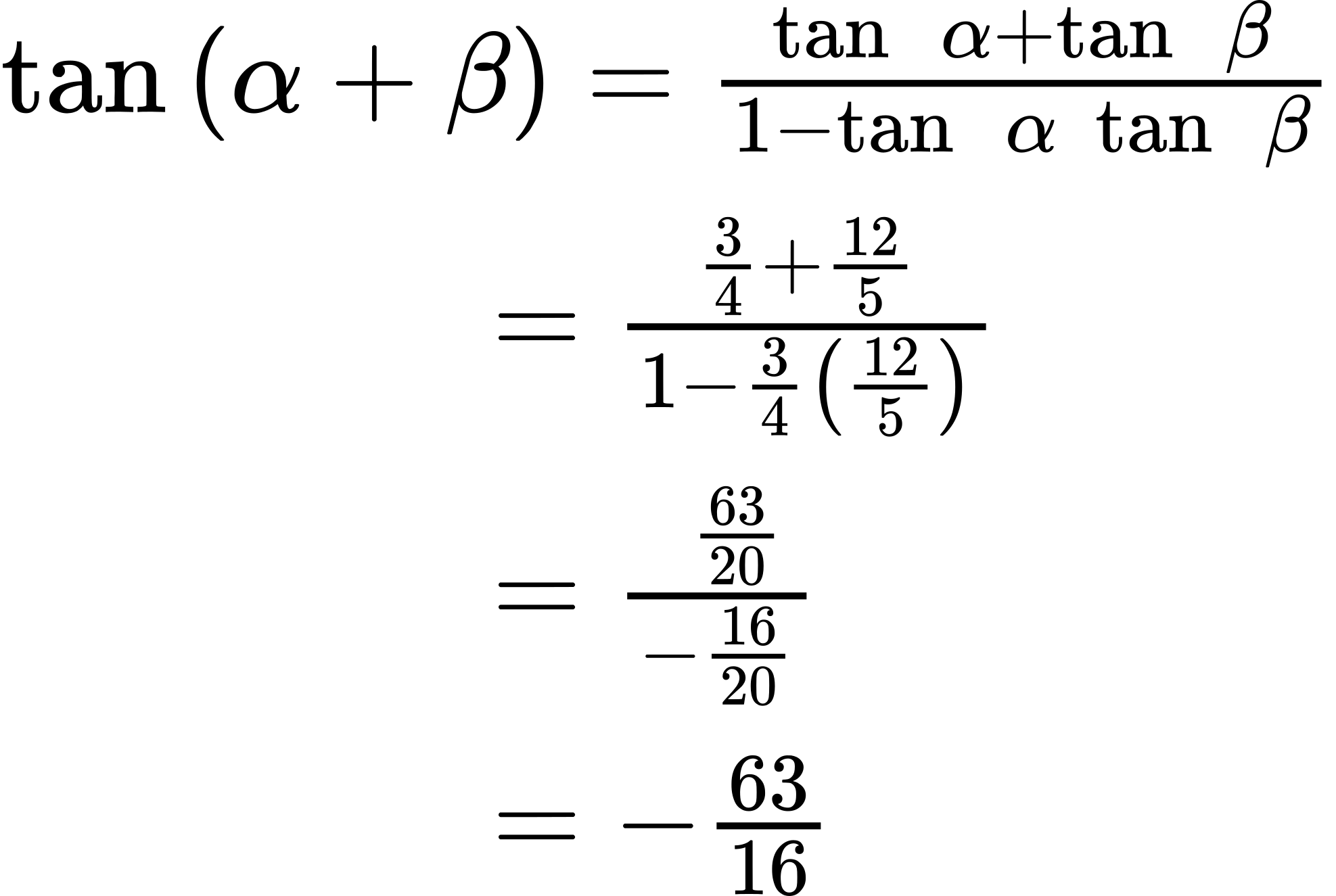
ⓓ To find [latex]tan[/latex] ([latex]α[/latex] − [latex]β[/latex]), we have the values we need. We can substitute them in and evaluate.
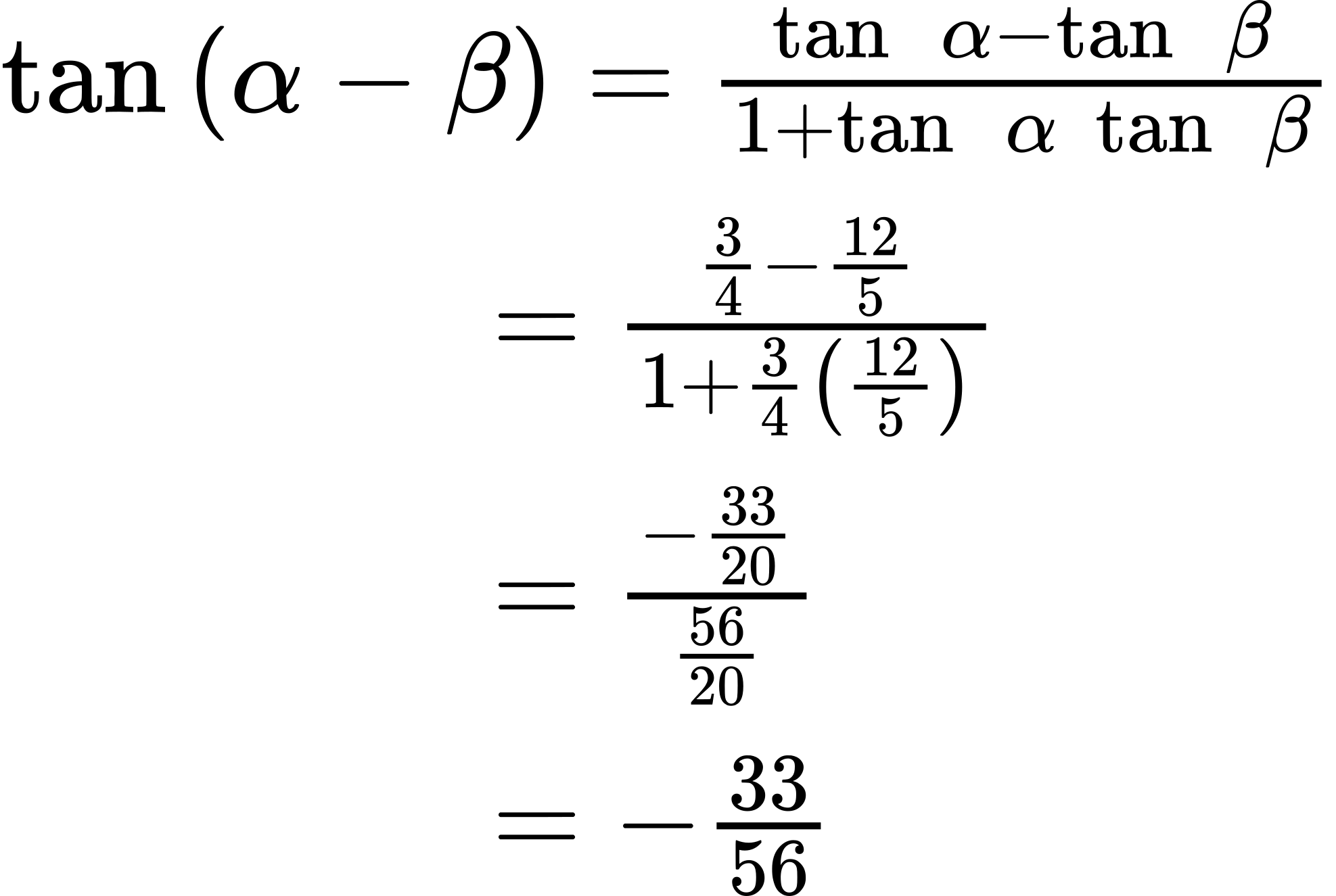
Analysis
A common mistake when addressing problems such as this one is that we may be tempted to think that [latex]α[/latex] and [latex]β[/latex] are angles in the same triangle, which of course, they are not. Also note that:
Using Sum and Difference Formulas for Cofunctions
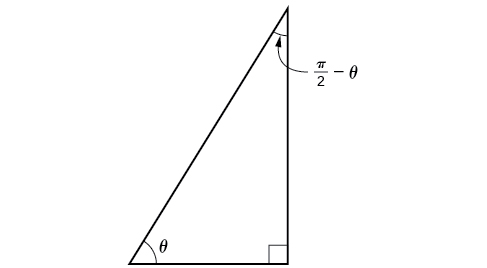
Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall from Right Triangle Trigonometry that, if the sum of two positive angles is [latex]\frac{π}{2}[/latex], those two angles are complements, and the sum of the two acute angles in a right triangle is [latex]\frac{π}{2}[/latex], so they are also complements. In Figure 6, notice that if one of the acute angles is labeled as [latex]θ[/latex], then the other acute angle must be labeled ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]).
Notice also that [latex]sin θ[/latex] = [latex]cos[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]): opposite over hypotenuse. Thus, when two angles are complementary, we can say that the sine of [latex]θ[/latex] equals the cofunction of the complement of [latex]θ[/latex]. Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.
From these relationships, the cofunction identities are formed.
Cofunction Identities
The cofunction identities are summarized in Table 2.
|
[latex]sin θ[/latex] = [latex]cos[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex])
|
[latex]cos θ[/latex] = [latex]sin[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]) |
|
[latex]tan θ[/latex] = [latex]cot[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex])
|
[latex]cot θ[/latex] = [latex]tan[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]) |
| [latex]sec θ[/latex] = [latex]csc[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]) | [latex]csc θ[/latex] = [latex]sec[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]) |
Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using:
we can write:
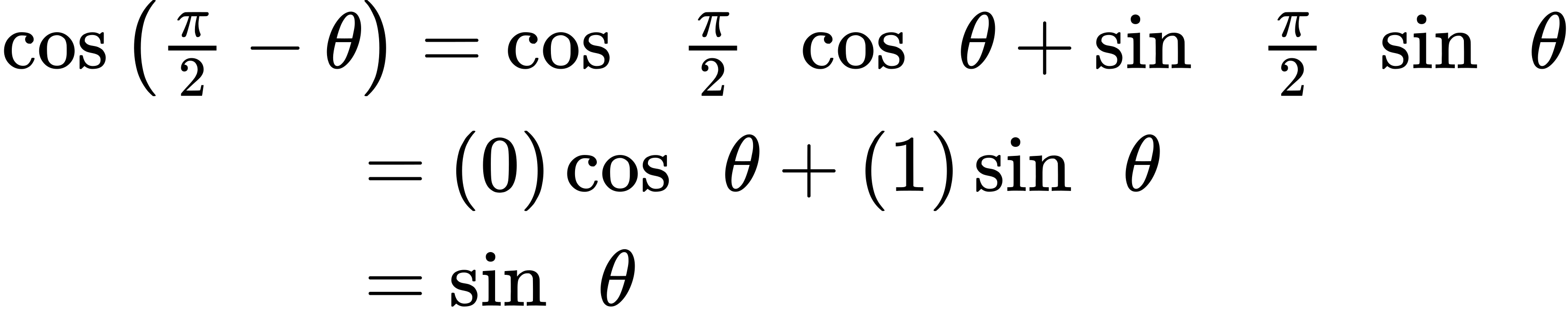
Example 7
Finding a Cofunction with the Same Value as the Given Expression
Write [latex]tan[/latex] [latex]\frac{π}{9}[/latex] in terms of its cofunction.
Show/Hide Solution
Solution
The cofunction of [latex]tan θ[/latex] = [latex]cot[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex]).
Thus,
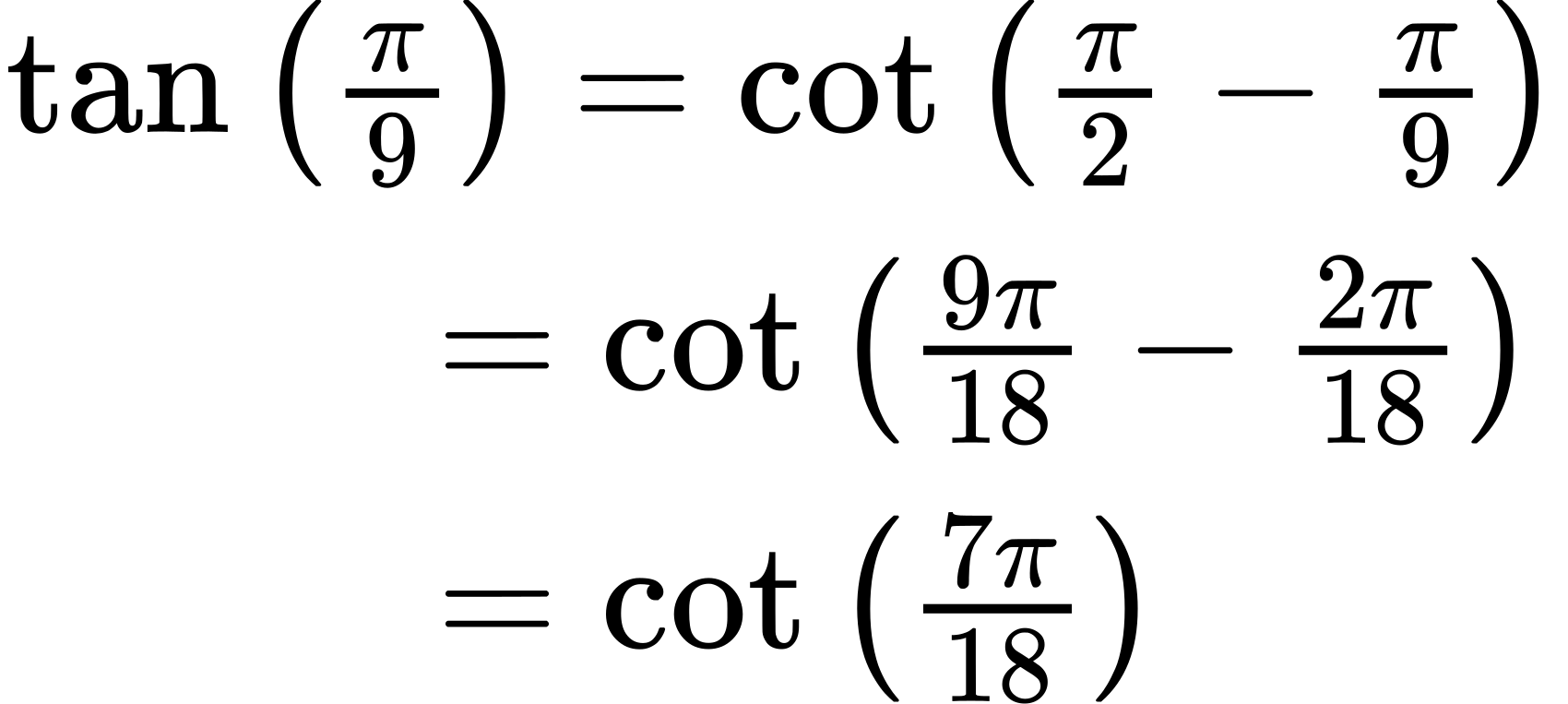
Try It #4
Write [latex]sin[/latex] [latex]\frac{π}{7}[/latex] in terms of its cofunction.
Using the Sum and Difference Formulas to Verify Identities
Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems. Reviewing the general rules from Solving Trigonometric Equations with Identities may help simplify the process of verifying an identity.
How To
Given an identity, verify using sum and difference formulas.
- Begin with the expression on the side of the equal sign that appears most complex. Rewrite that expression until it matches the other side of the equal sign. Occasionally, we might have to alter both sides, but working on only one side is the most efficient.
- Look for opportunities to use the sum and difference formulas.
- Rewrite sums or differences of quotients as single quotients.
- If the process becomes cumbersome, rewrite the expression in terms of sines and cosines.
Example 8
Verifying an Identity Involving Sine
Verify the identity [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]) + [latex]sin[/latex] ([latex]α[/latex] − [latex]β[/latex]) = 2 [latex]sin α[/latex] [latex]cos β[/latex].
Show/Hide Solution
Solution
We see that the left side of the equation includes the sines of the sum and the difference of angles.
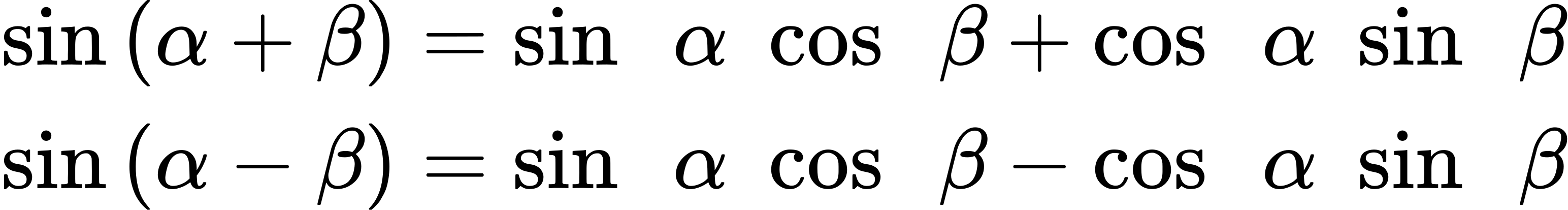
We can rewrite each using the sum and difference formulas.
![]()
We see that the identity is verified.
Example 9
Verifying an Identity Involving Tangent
Verify the following identity.
[latex]\dfrac{sin(α − β)}{cos α cos β}[/latex] = [latex]tan α[/latex] − [latex]tan β[/latex]
Show/Hide Solution
Solution
We can begin by rewriting the numerator on the left side of the equation.

We see that the identity is verified. In many cases, verifying tangent identities can successfully be accomplished by writing the tangent in terms of sine and cosine.
Try It #5
Verify the identity: [latex]tan[/latex] ([latex]π[/latex] − [latex]θ[/latex]) = − [latex]tan θ[/latex].
Example 10
Using Sum and Difference Formulas to Solve an Application Problem
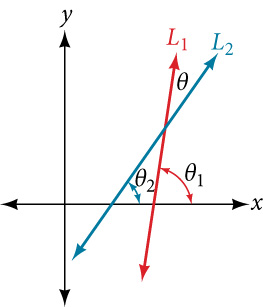
Let [latex]L_1[/latex] and [latex]L_2[/latex] denote two non-vertical intersecting lines, and let [latex]θ[/latex] denote the acute angle between [latex]L_1[/latex] and [latex]L_2[/latex]. See Figure 7. Show that:
where [latex]m_1[/latex] and [latex]m_2[/latex] are the slopes of [latex]L_1[/latex] and [latex]L_2[/latex] respectively. (Hint: Use the fact that [latex]tan θ_1[/latex] = [latex]m_1[/latex] and [latex]tan θ_2[/latex] = [latex]m_2[/latex]).
Show/Hide Solution
Solution
Using the difference formula for tangent, this problem does not seem as daunting as it might.
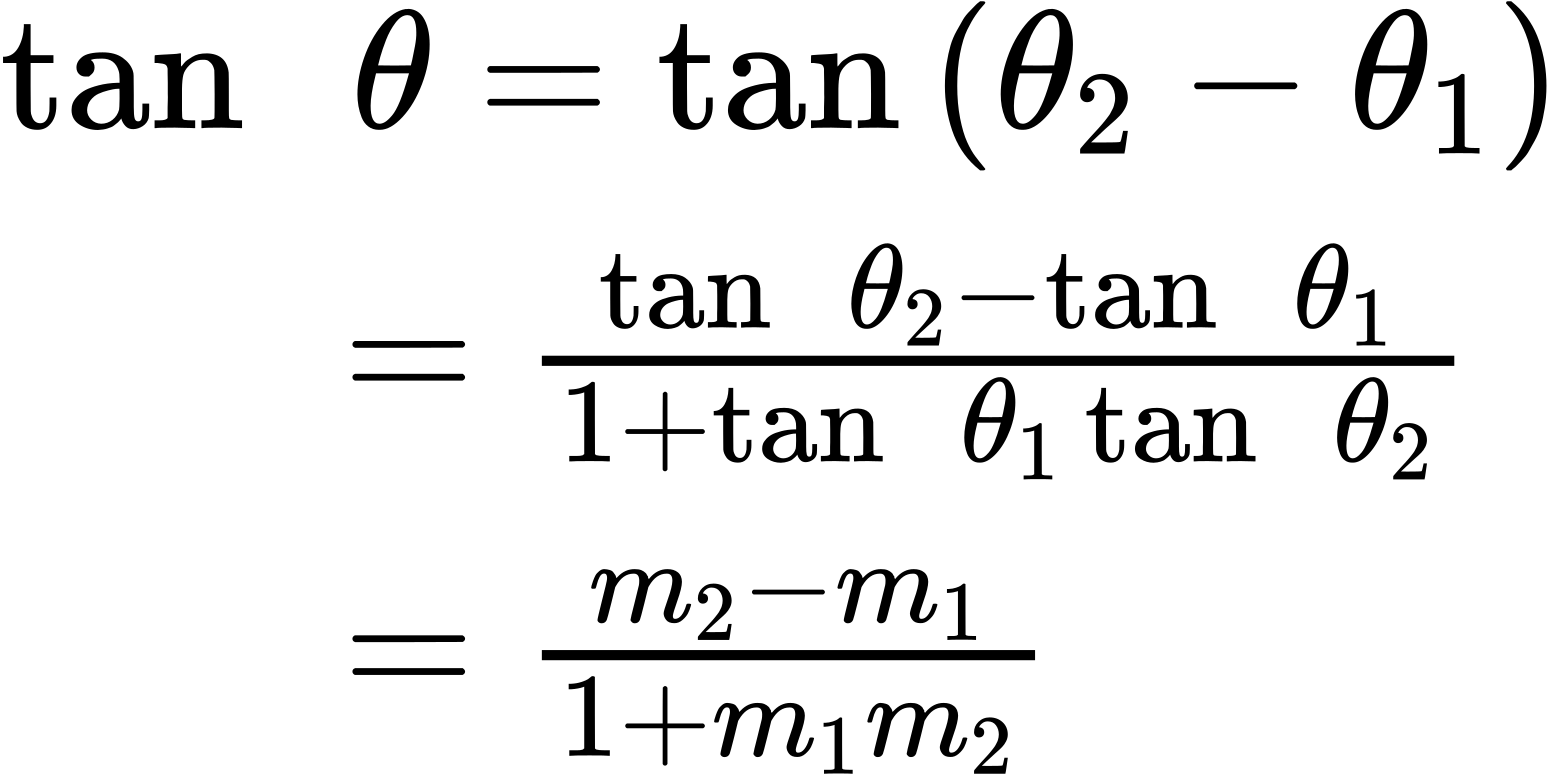
Example 11
Investigating a Guy-wire Problem
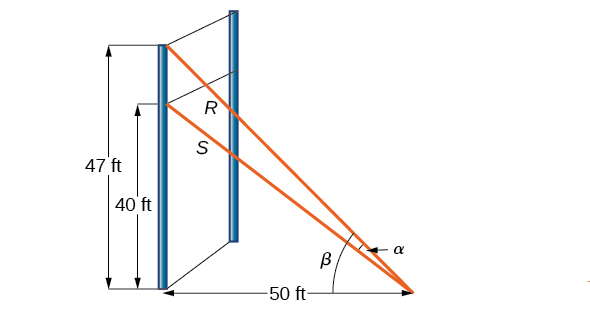
For a climbing wall, a guy-wire [latex]R[/latex] is attached 47 feet high on a vertical pole. Added support is provided by another guy-wire [latex]S[/latex] attached 40 feet above ground on the same pole. If the wires are attached to the ground 50 feet from the pole, find the angle [latex]α[/latex] between the wires. See Figure 8.
Show/Hide Solution
Solution
Let’s first summarize the information we can gather from the diagram. As only the sides adjacent to the right angle are known, we can use the tangent function. Notice that [latex]tan β[/latex] = [latex]\frac{47}{50}[/latex], and [latex]tan[/latex] ([latex]β[/latex] − [latex]α[/latex]) = [latex]\frac{40}{50}[/latex] = [latex]\frac{4}{5}[/latex]. We can then use difference formula for tangent.
Now, substituting the values we know into the formula, we have
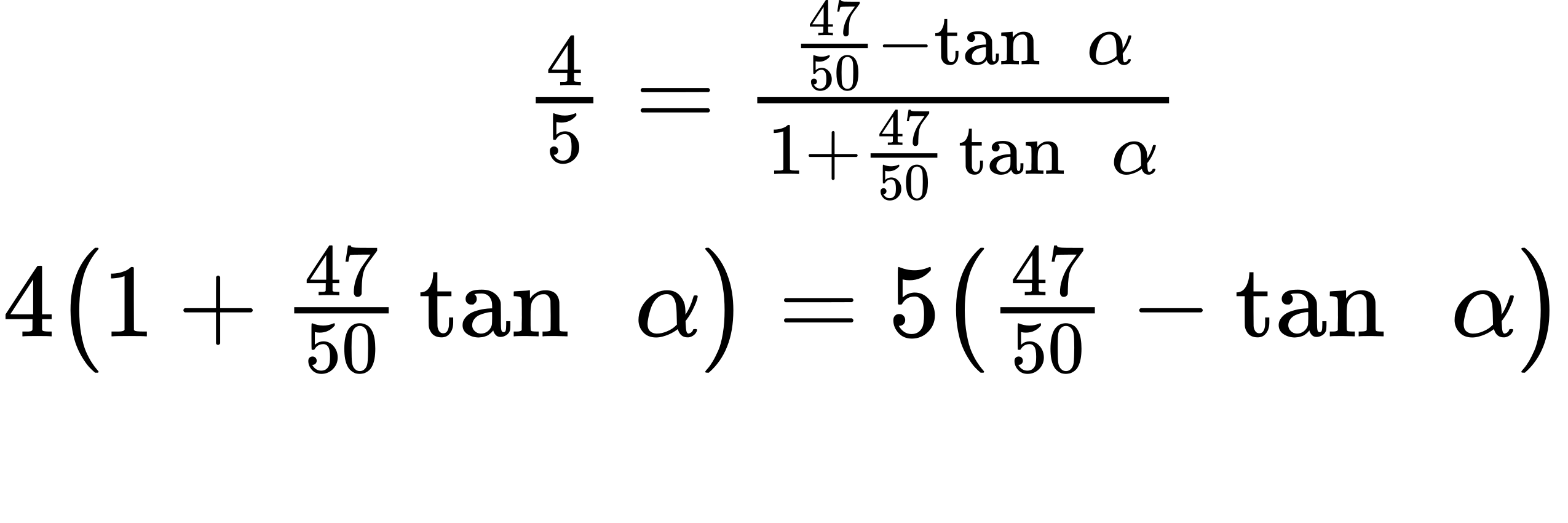
Use the distributive property, and then simplify the functions.
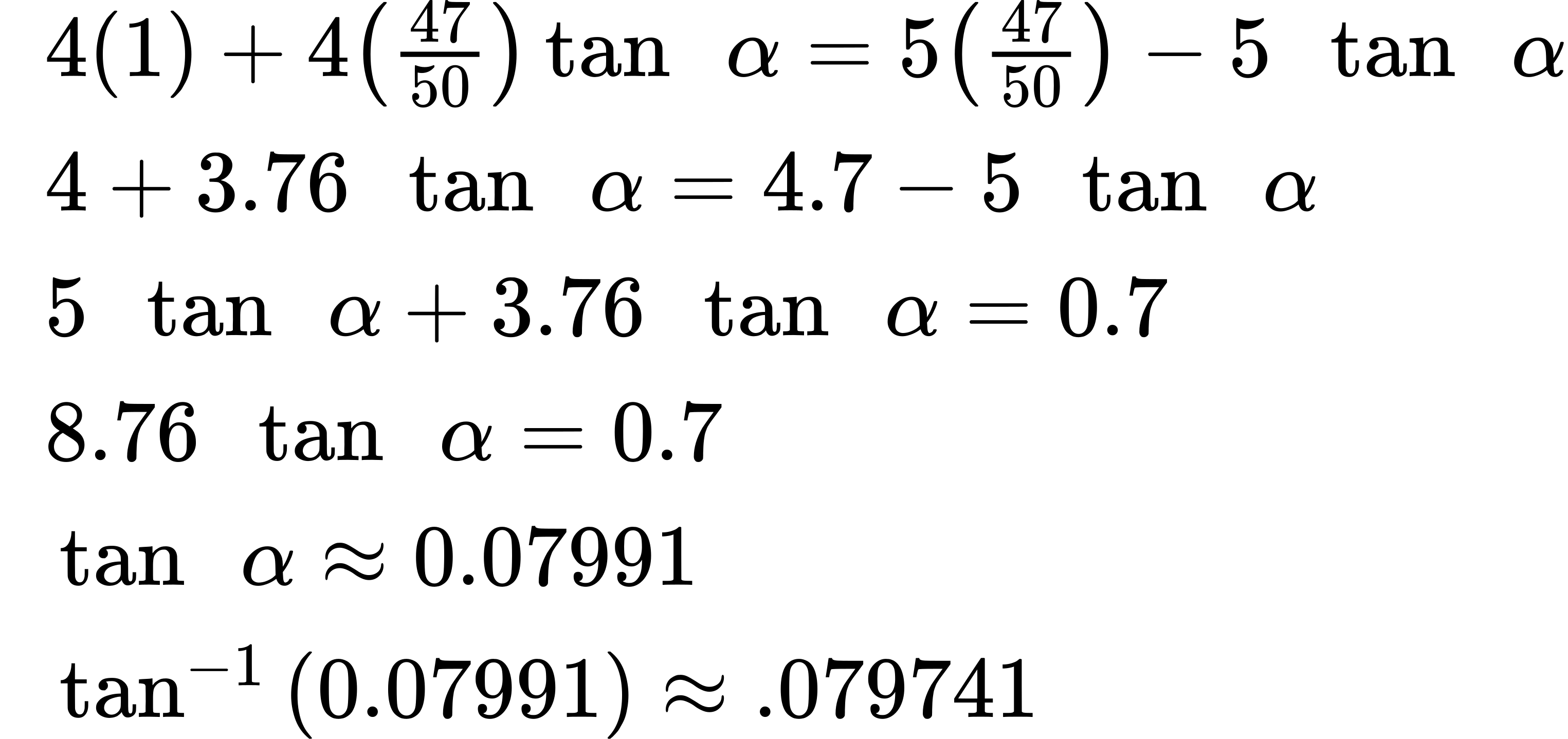
Now we can calculate the angle in degrees.
Analysis
Occasionally, when an application appears that includes a right triangle, we may think that solving is a matter of applying the Pythagorean Theorem. That may be partially true, but it depends on what the problem is asking and what information is given.
Media
Access these online resources for additional instruction and practice with sum and difference identities.
- Sum and Difference Identities for Cosine
- Sum and Difference Identities for Sine
- Sum and Difference Identities for Tangent
Section Exercises
Verbal
1. Explain the basis for the cofunction identities and when they apply.
2. Is there only one way to evaluate [latex]cos[/latex] ([latex]\frac{5π}{4}[/latex])? Explain how to set up the solution in two different ways, and then compute to make sure they give the same answer.
3. Explain to someone who has forgotten the even-odd properties of sinusoidal functions how the addition and subtraction formulas can determine this characteristic for [latex]f(x)[/latex] = [latex]sin (x)[/latex] and [latex]g(x)[/latex] = [latex]cos (x)[/latex]. (Hint: 0 − [latex]x[/latex] = −[latex]x[/latex])
Algebraic
For the following exercises, find the exact value.
4. [latex]cos[/latex] ([latex]\frac{7π}{12}[/latex])
5. [latex]cos[/latex] ([latex]\frac{π}{12}[/latex])
6. [latex]sin[/latex] ([latex]\frac{5π}{12}[/latex])
7. [latex]sin[/latex] ([latex]\frac{11π}{12}[/latex])
8. [latex]tan[/latex] (−[latex]\frac{π}{12}[/latex])
9. [latex]tan[/latex] ([latex]\frac{19π}{12}[/latex])
For the following exercises, rewrite in terms of [latex]sin[/latex] [latex]x[/latex] and [latex]cos[/latex] [latex]x[/latex].
10. [latex]sin[/latex] ([latex]x[/latex] + [latex]\frac{11π}{6}[/latex])
11. [latex]sin[/latex] ([latex]x[/latex] − [latex]\frac{3π}{4}[/latex])
12. [latex]cos[/latex] ([latex]x[/latex] − [latex]\frac{5π}{6}[/latex])
13. [latex]cos[/latex] ([latex]x[/latex] + [latex]\frac{2π}{3}[/latex])
For the following exercises, simplify the given expression.
14. [latex]csc[/latex] ([latex]\frac{π}{2}[/latex] − [latex]t[/latex])
15. [latex]sec[/latex] ([latex]\frac{π}{2}[/latex] − [latex]θ[/latex])
16. [latex]cot[/latex] ([latex]\frac{π}{2}[/latex] − [latex]x[/latex])
17. [latex]tan[/latex] ([latex]\frac{π}{2}[/latex] − [latex]x[/latex])
18. [latex]sin[/latex] ([latex]2x[/latex]) [latex]cos[/latex] ([latex]5x[/latex]) − [latex]sin[/latex] ([latex]5x[/latex]) [latex]cos[/latex] ([latex]2x[/latex])
19. [latex]\frac{tan (\frac{3}{2}x) − tan (\frac{7}{5}x)}{1 + tan (\frac{3}{2}x) tan (\frac{7}{5}x)}[/latex]
For the following exercises, find the requested information.
20. Given that [latex]sin[/latex] [latex]a[/latex] = [latex]\frac{2}{3}[/latex] and [latex]cos[/latex] [latex]b[/latex] = −[latex]\frac{1}{4}[/latex], with [latex]a[/latex] and [latex]b[/latex] both in the interval [[latex]\frac{π}{2}[/latex] , [latex]π[/latex]), find [latex]sin[/latex] ([latex]a[/latex] + [latex]b[/latex]) and [latex]cos[/latex] ([latex]a[/latex] − [latex]b[/latex]).
21. Given that [latex]sin[/latex] [latex]a[/latex] = [latex]\frac{4}{5}[/latex] and [latex]cos[/latex] [latex]b[/latex] = −[latex]\frac{1}{3}[/latex], with [latex]a[/latex] and [latex]b[/latex] both in the interval [[latex]0[/latex], [latex]π[/latex]), find [latex]sin[/latex] ([latex]a[/latex] − [latex]b[/latex]) and [latex]cos[/latex] ([latex]a[/latex] + [latex]b[/latex]).
For the following exercises, find the exact value of each expression.
22. [latex]sin[/latex] ([latex]cos^{−1}[/latex]([latex]0[/latex]) − [latex]cos^{−1}[/latex]([latex]\frac{1}{2}[/latex]))
23. [latex]cos[/latex] ([latex]cos^{−1}[/latex]([latex]\frac{\sqrt{2}}{2}[/latex]) + [latex]sin^{−1}[/latex]([latex]\frac{\sqrt{3}}{2}[/latex]))
24. [latex]tan[/latex] ([latex]sin^{−1}[/latex]([latex]\frac{1}{2}[/latex]) − [latex]cos^{−1}[/latex]([latex]\frac{1}{2}[/latex]))
Graphical
For the following exercises, simplify the expression, and then graph both expressions as functions to verify the graphs are identical.
25. [latex]cos[/latex] ([latex]\frac{π}{2}[/latex] − [latex]x[/latex])
26. [latex]sin[/latex] ([latex]π[/latex] − [latex]x[/latex])
27. [latex]tan[/latex] ([latex]\frac{π}{3}[/latex] + [latex]x[/latex])
28. [latex]sin[/latex] ([latex]\frac{π}{3}[/latex] + [latex]x[/latex])
29. [latex]tan[/latex] ([latex]\frac{π}{4}[/latex] − [latex]x[/latex])
30. [latex]cos[/latex] ([latex]\frac{7π}{6}[/latex] + [latex]x[/latex])
31. [latex]sin[/latex] ([latex]\frac{π}{4}[/latex] + [latex]x[/latex])
32. [latex]cos[/latex] ([latex]\frac{5π}{4}[/latex] + [latex]x[/latex])
For the following exercises, use a graph to determine whether the functions are the same or different. If they are the same, show why. If they are different, replace the second function with one that is identical to the first. (Hint: think [latex]2x[/latex] = [latex]x[/latex] + [latex]x[/latex])
33. [latex]f(x)[/latex] = [latex]sin[/latex] ([latex]4x[/latex]) − [latex]sin[/latex] ([latex]3x[/latex]) [latex]cos[/latex] [latex]x[/latex], [latex]g(x)[/latex] = [latex]sin[/latex] [latex]x[/latex] [latex]cos[/latex] ([latex]3x[/latex])
34. [latex]f(x)[/latex] = [latex]cos[/latex] ([latex]4x[/latex]) + [latex]sin[/latex] [latex]x[/latex] [latex]sin[/latex] ([latex]3x[/latex]), [latex]g(x)[/latex] = −[latex]cos[/latex] [latex]x[/latex] [latex]cos[/latex] ([latex]3x[/latex])
35. [latex]f(x)[/latex] = [latex]sin[/latex] ([latex]3x[/latex]) [latex]cos[/latex] ([latex]6x[/latex]), [latex]g(x)[/latex] = −[latex]sin[/latex] ([latex]3x[/latex]) [latex]cos[/latex] ([latex]6x[/latex])
36. [latex]f(x)[/latex] = [latex]sin[/latex] ([latex]4x[/latex]), [latex]g(x)[/latex] = [latex]sin[/latex] ([latex]5x[/latex]) [latex]cos[/latex] [latex]x[/latex] − [latex]cos[/latex] ([latex]5x[/latex]) [latex]sin[/latex] [latex]x[/latex]
37. [latex]f(x)[/latex] = [latex]sin[/latex] ([latex]2x[/latex]), [latex]g(x)[/latex] = 2 [latex]sin[/latex] [latex]x[/latex] [latex]cos[/latex] [latex]x[/latex]
38. [latex]f(θ)[/latex] = [latex]cos[/latex] ([latex]2θ[/latex]), [latex]g(θ)[/latex] = [latex]cos[/latex] ([latex]2θ[/latex]) − [latex]sin[/latex] ([latex]2θ[/latex])
39. [latex]f(θ)[/latex] = [latex]tan[/latex] ([latex]2θ[/latex]), [latex]g(θ)[/latex] = [latex]\frac{tan θ}{1 + tan (2θ)}[/latex]
40. [latex]f(x)[/latex] = [latex]sin[/latex] ([latex]3x[/latex]) [latex]sin[/latex] [latex]x[/latex], [latex]g(x)[/latex] = [latex]sin^2[/latex] ([latex]2x[/latex]) [latex]cos^2 x[/latex] − [latex]cos^2[/latex] ([latex]2x[/latex]) [latex]sin[/latex] ([latex]2x[/latex])
41. [latex]f(x)[/latex] = [latex]tan[/latex] (−[latex]x[/latex]), [latex]g(x)[/latex] = [latex]\frac{tan x − tan(2x)}{1 − tan x tan (2x)}[/latex]
Extensions
For the following exercises, prove or disprove the statements.
42. [latex]tan[/latex] ([latex]u[/latex] + [latex]v[/latex]) = [latex]\frac{tan u + tan v}{1 − tan u tan v}[/latex]
43. [latex]tan[/latex] ([latex]u[/latex] − [latex]v[/latex]) = [latex]\frac{tan u − tan v}{1 + tan u tan v}[/latex]
44. [latex]\frac{tan (x + y)}{1 + tan x tan x}[/latex] = [latex]\frac{tan x + tan y}{1 − tan^2 x tan^2 y}[/latex]
45. If [latex]α[/latex], [latex]β[/latex], and [latex]γ[/latex] are angles in the same triangle, then prove or disprove [latex]sin[/latex] ([latex]α[/latex] + [latex]β[/latex]) = [latex]sin[/latex] [latex]γ[/latex].
46. If [latex]α[/latex], [latex]β[/latex], and [latex]γ[/latex] are angles in the same triangle, then prove or disprove [latex]tan[/latex] [latex]α[/latex] + [latex]tan[/latex] [latex]β[/latex] + [latex]tan[/latex] [latex]γ[/latex] = [latex]tan[/latex] [latex]α[/latex] [latex]tan[/latex] [latex]β[/latex] [latex]tan[/latex] [latex]γ[/latex].
For the following exercises, prove the identities provided.
47. [latex]tan[/latex] ([latex]x[/latex] + [latex]\frac{π}{4}[/latex]) = [latex]\frac{tan x + 1}{1 − tan x}[/latex]
48. [latex]\frac{tan (a + b)}{tan (a − b)}[/latex] = [latex]\frac{sin a cos a + sin b cos b}{sin a cos a − sin b cos b}[/latex]
59. [latex]\frac{cos(a + b)}{cos a cos b}[/latex]= 1 − [latex]tan[/latex] [latex]a[/latex] [latex]tan[/latex] [latex]b[/latex]
50. [latex]cos[/latex] ([latex]x[/latex] + [latex]y[/latex]) [latex]cos[/latex] ([latex]x[/latex] − [latex]y[/latex]) = [latex]cos^2[/latex] [latex]x[/latex] − [latex]sin^2[/latex] [latex]y[/latex]
51. [latex]\frac{cos (x + h) − cos x}{h}[/latex] = [latex]cos[/latex] [latex]x[/latex] [latex]\frac{cos h − 1}{h}[/latex] − [latex]sin[/latex] [latex]x[/latex] [latex]\frac{sin h}{h}[/latex]

