Chapter 1 – Functions
“Try It” Exercises
Section 1.1 – Functions and Function Notation
1.
- ⓐ yes
- ⓑ yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)
2. w=f(d)
3. yes
4. g5=1
5. m=8
6. y=fx=x32
7. g1=8
8. x=0 or x=2
9.
- ⓐ yes, because each bank account has a single balance at any given time
- ⓑ no, because several bank account numbers may have the same balance
- ⓒ no, because the same output may correspond to more than one input.
10.
- ⓐ Yes, letter grade is a function of percent grade;
- ⓑ No, it is not one-to-one. There are 100 different percent numbers we could get but only about five possible letter grades, so there cannot be only one percent number that corresponds to each letter grade.
11. yes
12. No, because it does not pass the horizontal line test.
Section 1.2 – Domain and Range
1. {−5, 0, 5, 10, 15}
2. (−∞,∞)
3. (−∞,12)∪(12,∞)
4. [latex][−\frac{5}{2},∞)[/latex]
5.
ⓐ values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3;
ⓑ {x|x≤−2 or −1≤x<3};
ⓒ (−∞,−2]∪[−1,3)
6. domain =[1950,2002] range = [47,000,000,89,000,000]
7. domain: (−∞,2]; range: (−∞,0]
8.
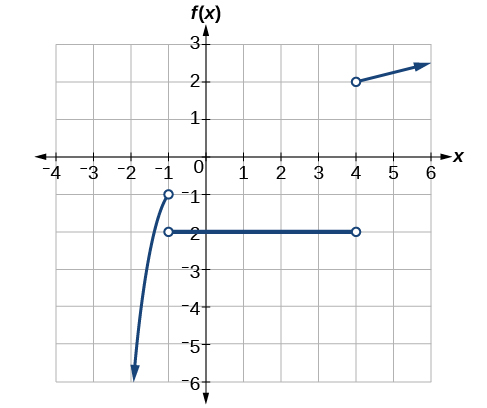
Section Exercises
Section 1.1 – Functions and Function Notation
1. A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.
3. When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.
5. When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.
7. function
9. function
11. function
13. function
15. function
17. function
19. function
21. function
23. function
25. not a function
27. [latex]f(−3)=−11[/latex]; [latex]f(2)=−1[/latex];
[latex]f(−a)=−2a−5;[/latex]
[latex]−f(a)=−2a+5;[/latex]
[latex]f(a+h)=2a+2h−5[/latex]
29. [latex]f(−3)=\sqrt{5}+5[/latex]; [latex]f(2)=5[/latex];
[latex]f(−a)=\sqrt{2+a}+5;[/latex]
[latex]−f(a)=-\sqrt{2−a}−5;[/latex]
[latex]f(a+h)=\sqrt{2−a−h}+5[/latex]
31. [latex]f(−3)=2[/latex]; [latex]f(2)=1−3=−2[/latex];
[latex]f(−a)=|−a−1|−|−a+1|;[/latex]
[latex]−f(a)=−|a−1|+|a+1|;[/latex]
[latex]f(a+h)=|a+h−1|−|a+h+1[/latex]
33. [latex]\frac{g(x)−g(a)}{x−a}=x+a+2[/latex], x≠a
35.
ⓐ f(−2)=14;
ⓑ x=3
37.
ⓐ f(5)=10;
ⓑ x=−1 or x=4
39.
ⓐ f(t)=6−23t;
ⓑ f(−3)=8;
ⓒ t=6
41. not a function
43. function
45. function
47. function
49. function
51. function
53.
ⓐ f(0)=1;
ⓑ f(x)=−3, x=−2 or
55. not a function so it is also not a one-to-one function
57. one-to-one function
59. function, but not one-to-one
61. function
63. function
65. not a function
67. f(x)=1, x=2
69.
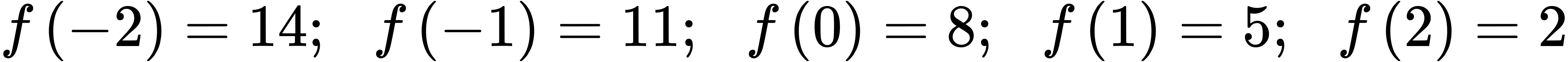
71.
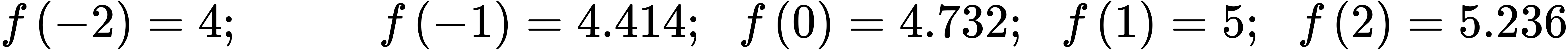
73.
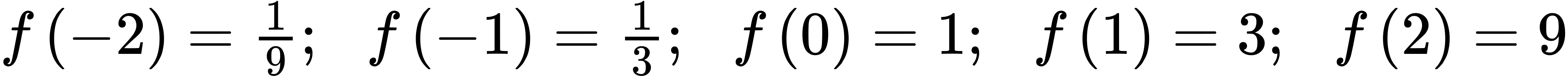
75. 20
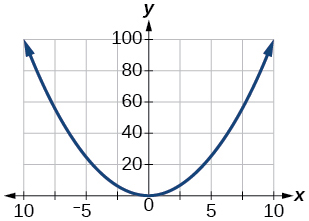
77. [0, 100]
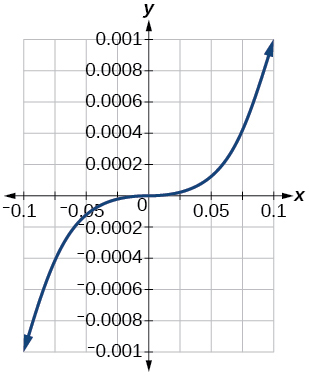
79. [−0.001, 0.001]
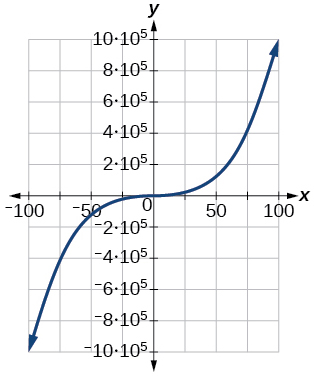
81. [−1,000,000, 1,000,000]
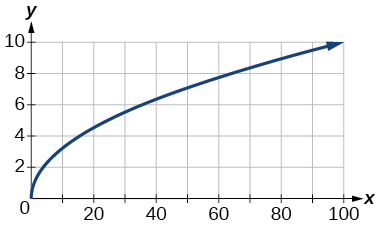
83. [0, 10]
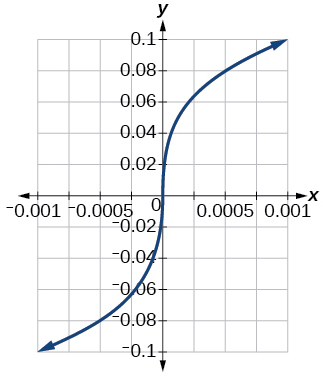
85. [−0.1,0.1]
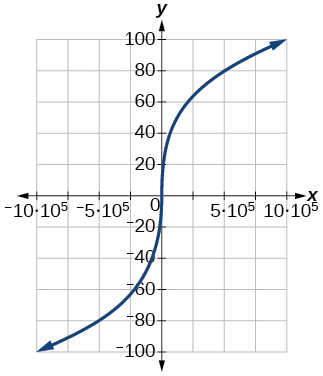
87. [−100, 100]
89.
ⓐ g(5000)=50;
ⓑ The number of cubic yards of dirt required for a garden of 100 square feet is 1.
91.
ⓐ The height of a rocket above ground after 1 second is 200 ft.
ⓑ the height of a rocket above ground after 2 seconds is 350 ft.
Section 1.2 – Domain and Range
1. The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.
3. There is no restriction on x for f(x)=x3 because you can take the cube root of any real number. So the domain is all real numbers, (−∞,∞). When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x-values are restricted for f(x)=x to nonnegative numbers and the domain is [0,∞).
5. Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x-axis and y-axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate −∞ or ∞. Combine the graphs to find the graph of the piecewise function.
7. (−∞,∞)
9. (−∞,3]
11. (−∞,∞)
13. (−∞,∞)
15. (−∞,−12)∪(−12,∞)
17. (−∞,−11)∪(−11,2)∪(2,∞)
19. (−∞,−3)∪(−3,5)∪(5,∞)
21. (−∞,5)
23. [6,∞)
25. (−∞,−9)∪(−9,9)∪(9,∞)
27. domain: (2,8], range: [6,8)
29. domain: [−4, 4], range: [0, 2]
31. domain: [−5, 3), range: [0,2]
33. domain: (−∞,1], range: [0,∞)
35. domain: [latex][−6,−\frac{1}{6}]∪[\frac{1}{6},6][/latex]; range: [latex][−6,−\frac{1}{6}]∪[\frac{1}{6},6][/latex]
37. domain: [−3, ∞); range: [0,∞)
39. domain: (−∞,∞)
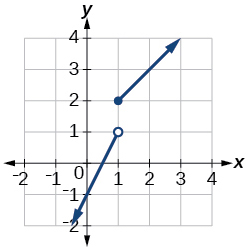
41. domain: (−∞,∞)
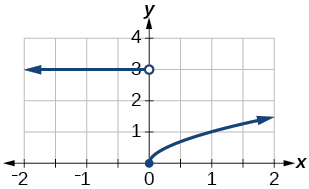
43. domain: (−∞,∞)
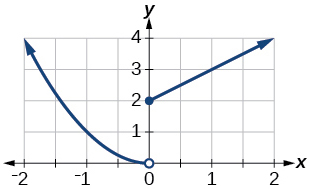
45. domain: (−∞,∞)
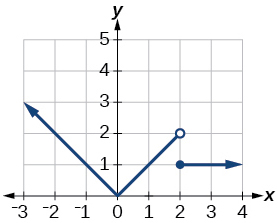
47.
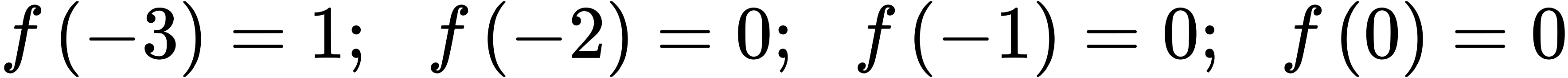
49.
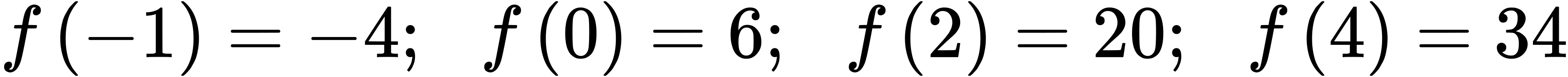
51.

53. domain: (−∞,1)∪(1,∞)
55.
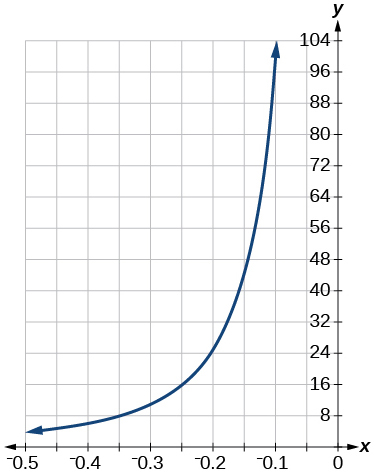
window: [−0.5,−0.1]; range: [4, 100]
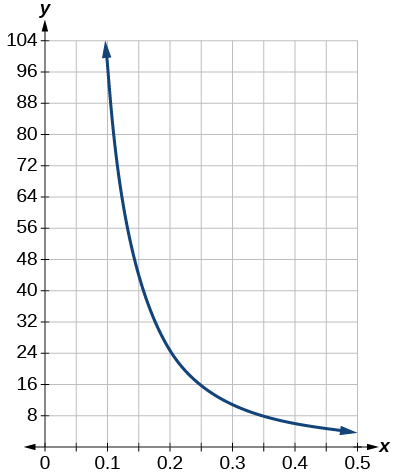
window: [0.1, 0.5]; range: [4, 100]
57. [0, 8]
59. Many answers. One function is [latex]f(x)=\frac{1}{\sqrt{x−2}}[/latex].

