Introduction to Trigonometric Identities and Equations
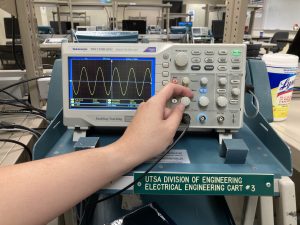
Math is everywhere, even in places we might not immediately recognize. For example, mathematical relationships describe the transmission of images, light, sound, and currents. As part of their coursework at UTSA, engineering students working in the circuitry lab read and analyze signals from a circuit using a digital oscilloscope. Sometimes these signals take the form of a sine wave.
The sinusoidal graph in the figure above represents an alternating current in a circuit. Such graphs are described using trigonometric equations and functions. In this chapter, we will manipulate trigonometric equations algebraically by applying various formulas and trigonometric identities. We will also explore methods for solving linear and quadratic equations involving trigonometric functions of angles and double angles over a given interval using the trigonometric identities previously studied. Finally, we will investigate some of the ways that trigonometric equations are used to model real-life phenomena, as you can see in the sine wave pictured above!
♠ ♣ ♥ ♦
In Chapter 4, you use the Pythagorean identities, even-odd identities, reciprocal identities, and quotient identities to manipulate trigonometric equations algebraically. You will also use the sum and difference identities to evaluate the six trigonometric functions at angles that sum or differ to known key angles from the unit circle. You will also explore the double-angle formulas (a special case of the sum formulas) and half-angle formulas to find exact values of trigonometric functions. You will also have the opportunity to use the product-to-sum formula to solve for the exact value of the product of sines and cosines evaluated at non-key angles from the unit circle.
These are just a few of the important concepts and ideas included in Chapter 4. A complete list of the Key Takeaways from the chapter is organized in the table below:
Key Takeaways
- Prove simple identities using the fundamental identities and algebraic techniques.
- Understand how to establish identities.
- Use sum and difference formulas to find exact values, establish identities and evaluate compositions with inverse functions.
- Use double-angle formulas to find exact values.
- Use half-angle formulas to find exact values.
- Use product-to-sum and sum-to-product formulas.
- Apply double-angle formulas to solve trigonometric equations (including from applications).
- Solve linear, quadratic and other equations containing trigonometric functions, including those from application questions and those that can be solved using the Fundamental Identities.
- Find exact solutions in the interval [0, 2pi) and in general form for equations with a single trigonometric function.
- Use a calculator to find approximate solutions of trigonometric equations that require the use of an inverse function.

