Module 2.1 – Functions and Function Notation

Learning Objectives

In this section, you will:

  • Determine whether a relation represents a function.
  • Find the value of a function.
  • Determine whether a function is one-to-one.
  • Use the vertical line test to identify functions.
  • Graph the functions listed in the library of functions.

A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.

Determining Whether a Relation Represents a Function

A relation is a set of ordered pairs. The set consisting of the first components of each ordered pair is called the domain and the set consisting of the second components of each ordered pair is called the range. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.

\[

\{\, (1, 2), (2, 4), (3, 6), (4, 8), (5, 10) \,\}

\]

The domain is $\{\, 1, 2, 3, 4, 5 \,\}$. The range is $\{\, 2, 4, 6, 8, 10 \,\}$.

Note that each value in the domain is also known as an input value, or independent variable, and is often labeled with the lowercase letter $x$. Each value in the range is also known as an output value, or dependent variable, and is often labeled lowercase letter $y$.

A function $f$ is a relation that assigns a single element in the range to each element in the domain. In other words, no $x$-values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, $\{\, 1, 2, 3, 4, 5 \,\}$, is paired with exactly one element in the range, $\{\, 2, 4, 6, 8, 10 \,\}$.

Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as

\[

\{\, (\text{odd}, 1), (\text{even}, 2), (\text{odd}, 3), (\text{even}, 4), (\text{odd}, 5) \,\}

\]

Notice that each element in the domain, $\{\, \text{even}, \text{odd} \,\}$ is not paired with exactly one element in the range, $\{\, 1, 2, 3, 4, 5 \,\}$. For example, the term “odd” corresponds to three values from the domain, $\{\, 1, 3, 5 \,\}$ and the term “even” corresponds to two values from the range, $\{\, 2, 4 \,\}$. This violates the definition of a function, so this relation is not a function. Figure 1 compares relations that are functions and not functions.

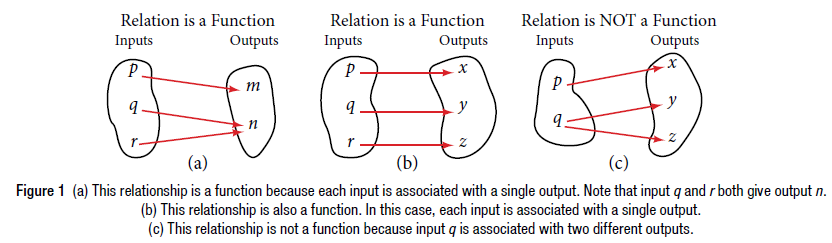
Image of 3 relations between inputs and outputs: (a) This relationship is a function because each input is associated with a single output. Note that input q and r both give output n. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input q is associated with two different outputs.

function
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain, and the output values make up the range.

How To…

Given a relationship between two quantities, determine whether the relationship is a function.

  1. Identify the input values.
  2. Identify the output values.
  3. If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.

Example 1  Determining If Menu Price Lists Are Functions

The coffee shop menu, shown in Figure 2 consists of items and their prices.

  1. Is price a function of the item?
  2. Is the item a function of the price?
Image of a menu with a Plain Donut costing 1.49, a Jelly Donut costing 1.99, and a Chocolate Donut costing 1.99.
Figure 2

Solution

  1. Let’s begin by considering the input as the items on the menu. The output values are then the prices. See Figure 2. Each item on the menu has only one price, so the price is a function of the item.
  2. Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it. See Figure 3.
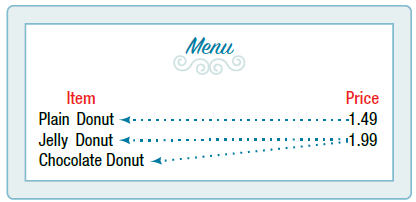
Image of menu with a price of 1.49 pointing back to a Plain Donut and a price of 1.99 pointing back to both a Jelly Donut and a Chocolate Donut.
Figure 3

Therefore, the item is a not a function of price.

Example 2  Determining If Class Grade Rules Are Functions

In a particular math class, the overall percent grade corresponds to a grade-point average. Is grade-point average a function of the percent grade? Is the percent grade a function of the grade-point average? Table 1 shows a possible rule for assigning grade points.

Table 1
Percent grade 0-56 57-61 62-66 67-71 72-77 78-86 87-91 92-100
Grade-point average 0.0 1.0 1.5 2.0 2.5 3.0 3.5 4.0

Solution   For any percent grade earned, there is an associated grade-point average, so the grade-point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade-point average.

In the grading system given, there is a range of percent grades that correspond to the same grade-point average. For example, students who receive a grade-point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade-point average.

Try It

Table 2 lists the five greatest baseball players of all time in order of rank.

Table 2
Player Rank
Babe Ruth 1
Willie Mays 2
Ty Cobb 3
Walter Johnson 4
Hank Aaron 5
  1. Is the rank a function of the player name?
  2. Is the player name a function of the rank?

Using Function Notation

Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into graphing calculators and computers. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions.

To represent “height is a function of age,” we start by identifying the descriptive variables h for height and a for age. The letters $f$, $g$, and $h$ are often used to represent functions just as we use $x$, $y$, and $z$ to represent numbers and $A$, $B$, and $C$ to represent sets.

\begin{align*}

&\text{$h$ is $f$ of $a$}   &   \text{We name the function $f$; height is a function of age.} \\

&$h = f(a)$   &   \text{We use parentheses to indicate the function input.} \\

&$f(a)$   &   \text{We name the function $f$; the expression is read as “$f$ of $a$.”}

\end{align*}

Remember, we can use any letter to name the function; the notation $h(a)$ shows us that $h$ depends on $a$. The value a must be put into the function $h$ to get a result. The parentheses indicate that age is input into the function; they do not indicate multiplication.

We can also give an algebraic expression as the input to a function. For example $f(a + b)$ means “first add $a$ and $b$, and the result is the input for the function $f$.” The operations must be performed in this order to obtain the correct result.

function notation
The notation $y = f(x)$ defines a function named $f$. This is read as “$y$ is a function of $x$.” The letter $x$ represents the input value, or independent variable. The letter $y$, or $f(x)$, represents the output value, or dependent variable.

Example 3  Using Function Notation for Days in a Month

Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.

Solution   The number of days in a month is a function of the name of the month, so if we name the function $f$, we write $\text{days} = f(\text{month})$ or $d = f(m)$. The name of the month is the input to a “rule” that associates a specific number (the output) with each input.

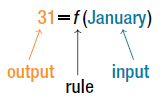
The equation 31 = f(January), where 31 is labeled as the output, f is labeled as the rule, and January is labeled as the input.
Figure 4

For example, $f(\text{March}) = 31$, because March has 31 days. The notation $d = f(m)$ reminds us that the number of days, $d$ (the output), is dependent on the name of the month, $m$ (the input).

Analysis   Note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.

Example 4  Interpreting Function Notation

A function $N = f (y)$ gives the number of police officers, $N$, in a town in year $y$. What does $f(2005) = 300$ represent?

Solution   When we read $f(2005) = 300$, we see that the input year is 2005. The value for the output, the number of police officers ($N$), is 300. Remember $N = f(y)$. The statement $f(2005) = 300$ tells us that in the year 2005 there were 300 police officers in the town.

Try It

Use function notation to express the weight of a pig in pounds as a function of its age in days $d$.

Q & A…

Instead of a notation such as $y = f(x)$, could we use the same symbol for the output as for the function, such as $y = y(x)$, meaning “$y$ is a function of $x$?”

Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as $f$, which is a rule or procedure, and the output $y$ we get by applying $f$ to a particular input $x$. This is why we usually use notation such as $y = f(x)$, $P = W(d)$, and so on.

Representing Functions Using Tables

A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases, these values represent all we know about the relationship; other times, the table provides a few select examples from a more complete relationship.

Table 3 lists the input number of each month ($\text{January} = 1$, $\text{February} = 2$, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function $f$ where $D = f(m)$ identifies months by an integer rather than by name.

Table 3
Month number, $m$ (input) 1 2 3 4 5 6 7 8 9 10 11 12
Days in month, $D$ (output) 31 28 31 30 31 30 31 31 30 31 30 31

Table 4 defines a function $Q = g(n)$. Remember, this notation tells us that $g$ is the name of the function that takes the input $n$ and gives the output $Q$.

Table 4
$n$ 1 2 3 4 5
$Q$ 8 6 7 6 8

Table 5 below displays the age of children in years and their corresponding heights. This table displays just some of the data available for the heights and ages of children. We can see right away that this table does not represent a function because the same input value, 5 years, has two different output values, 40 in. and 42 in.

Table 5
Age in years, $a$ (input) 5 5 6 7 8 9 10
Height in inches, $h$ (output) 40 42 44 47 50 52 54

How To…

Given a table of input and output values, determine whether the table represents a function.

  1. Identify the input and output values.
  2. Check to see if each input value is paired with only one output value. If so, the table represents a function.

Example 5  Identifying Tables that Represent Functions

Which table, Table 6, Table 7, or Table 8, represents a function (if any)?

Table 6
Input Output
2 1
5 3
8 6
Table 7
Input Output
-3 5
0 1
4 5
Table 8
Input Output
1 0
5 2
5 4

Solution   Table 6 and Table 7 define functions. In both, each input value corresponds to exactly one output value. Table 8 does not define a function because the input value of 5 corresponds to two different output values.

When a table represents a function, corresponding input and output values can also be specified using function notation.

The function represented by Table 6 can be represented by writing

\[

f(2) = 1 \text{, } f(5) = 3 \text{, and } f(8) = 6.

\]

Similarly, the statements

\[

g(−3) = 5 \text{, } g(0) = 1 \text{, and } g(4) = 5

\]

represent the function in table Table 7.

Table 8 cannot be expressed in a similar way because it does not represent a function.

Try It

Does Table 9 represent a function?

Table 9
Input Output
1 10
2 100
3 1000

Finding Input and Output values of a Function

When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.

When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the function’s formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.

Evaluation of Functions in Algebraic Forms

When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function $f(x) = 5 – 3x^{2}$ can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.

How To…

Given the formula for a function, evaluate.

  1. Replace the input variable in the formula with the value provided.
  2. Calculate the result.

Example 6  Evaluating Functions at Specific Values

Evaluate $f(x) = x^{2} + 3x – 4$ at:

  1. $2$
  2. $a$
  3. $a+h$
  4. $\dfrac{f(a+h) – f(a)}{h}$

Solution  Replace the $x$ in the function with each specified value.

  1. Because the input value is a number, 2, we can use simple algebra to simplify.
    \begin{align*}
    f(2) &= 2^{2} + 3(2) – 4 \\
    &= 4 + 6 – 4 \\
    &= 6
    \end{align*}
  2. In this case, the input value is a letter so we cannot simplify the answer any further.
    \[
    f(a) = a^{2} + 3a – 4
    \]
  3. With an input value of $a + h$, we must use the distributive property.
    \begin{align*}
    f(a+h) &= (a+h)^{2} + 3(a+h) – 4 \\
    &= a^{2} + 2ah + h^{2} + 3a + 3h – 4
    \end{align*}
  4. In this case, we apply the input values to the function more than once, and then perform algebraic operations on the result. We already found that
    \[
    f(a+h) = a^{2} + 2ah + h^{2} + 3a + 3h – 4
    \]
    and we know that
    \[
    f(a) = a^{2} + 3a – 4
    \]
    Now we combine the results and simplify.
    \begin{align*}
    \dfrac{f(a+h) – f(a)}{h} &= \dfrac{(a^{2} + 2ah + h^{2} + 3a + 3h – 4) – (a^{2} + 3a – 4)}{h} \\
    &= \dfrac{2ah + h^{2} + 3h}{h} \\
    &= \dfrac{h(2a + h + 3)}{h} \\
    &= 2a + h + 3
    \end{align*}

Example 7  Evaluating Functions

Given the function $h(p) = p^{2} + 2p$, evaluate $h(4)$.

Solution  To evaluate $h(4)$, we substitute the value 4 for the input variable $p$ in the given function.

\begin{align*}

h(p) &= p^{2} + 2p \\

h(4) &= (4)^{2} +2 (4) \\

&= 16 + 8 \\

&= 24

\end{align*}

Therefore, for an input of 4, we have an output of 24.

Try It

Given the function $g(m) = \sqrt{m-4}$ . Evaluate $g(5)$.

 

License

Mathematics for Business Copyright © by Jonathan Brucks. All Rights Reserved.

Share This Book