Module 7.2 – Exponential and Logarithmic Equations
Learning Objectives
In this section, you will:
- Use like bases to solve exponential equations.
- Use logarithms to solve exponential equations.
- Use the definition of a logarithm to solve logarithmic equations.
- Use the one-to-one property of logarithms to solve logarithmic equations.
- Solve applied problems involving exponential and logarithmic equations.

In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.
Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Using Like Bases to Solve Exponential Equations
The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers [latex]b, S, \text{ and } T[/latex], where [latex]b > 0, b \neq 1, b^{S} = b^{T} \text{ if and only if } S = T[/latex].
In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.
For example, consider the equation [latex]3^{4x − 7} = \dfrac{3^{2x}}{3}[/latex]. To solve for [latex]x[/latex], we use the division property of exponents to rewrite the right side so that both sides have the common base, 3. Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for [latex]x[/latex]:
\begin{align*}
3^{4x – 7} &= \dfrac{3^{2x}}{3}\\
3^{4x – 7} &= \dfrac{3^{2x}}{3^{1}} & \text{Rewrite 3 as } 3^{1}.\\
3^{4x – 7} &= 3^{2x – 1} & \text{Use the division property of exponents.}\\
4x – 7 &= 2x – 1 & \text{Apply the one-to-one property of exponents.}\\
2x &= 6 & \text{Subtract 2x and add 7 to both sides.}\\
x &= 3 & \text{Divide by 3.}
\end{align*}
using the one-to-one property of exponential functions to solve exponential equations
For any algebraic expressions [latex]S \text{ and } T[/latex], and any positive real number [latex]b \neq 1[/latex],
[latex]b^{S} = b^{T} \text{ if and only if } S = T[/latex]
How To…
Given an exponential equation with the form [latex]b^{S} = b^{T}[/latex], where [latex]S[/latex] and [latex]T[/latex] are algebraic expressions with an unknown, solve for the unknown.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form [latex]b^{S} = b^{T}[/latex].
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation, [latex]S = T[/latex], for the unknown.
Example 1 Solving an Exponential Equation with a Common Base
Solve [latex]2^{x - 1} = 2^{2x - 4}[/latex].
Solution
\begin{align*}
2^{x – 1} &= 2^{2x – 4} & \text{The common base is 2.}\\
x – 1 &= 2x – 4 & \text{By the one-to-one property the exponents must be equal.}\\
x &= 3 & \text{Solve for x.}
\end{align*}
Try it
Solve [latex]5^{2x} = 5^{3x + 2}[/latex].
Rewriting Equations So All Powers Have the Same Base
Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.
For example, consider the equation [latex]256 = 4^{x − 5}[/latex]. We can rewrite both sides of this equation as a power of [latex]2[/latex]. Then we apply the rules of exponents, along with the one-to-one property, to solve for [latex]x[/latex]:
\begin{align*}
256 &= 4^{x − 5}\\
2^{8} &= (2^{2})^{x – 5} & \text{Rewrite each side as a power with base 2.}\\
2^{8} &= 2^{2x – 10} & \text{Use the one-to-one property of exponents.}\\
8 &= 2x – 10 & \text{Apply the one-to-one property of exponents.}\\
18 &= 2x & \text{Add 10 to both sides.}\\
x &= 9 & \text{Divide by 2.}
\end{align*}
How To…
Given an exponential equation with unlike bases, use the one-to-one property to solve it.
- Rewrite each side in the equation as a power with a common base.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form [latex]b^{S} = b^{T}[/latex].
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation, [latex]S = T[/latex], for the unknown.
Example 2 Solving Equations by Rewriting Them to Have a Common Base
Solve [latex]8^{x + 2} = 16^{x + 1}[/latex].
Solution
\begin{align*}
8^{x + 2} &= 16^{x + 1}\\
(2^{3})^{x + 2} &= (2^{4})^{x + 1} & \text{Write 8 and 16 as powers of 2.}\\
2^{3x + 6} &= 2^{4x + 4} & \text{To take a power of a power, multiply exponents.}\\
3x + 6 &= 4x + 4 & \text{Use the one-to-one property to set the exponents equal.}\\
x &= 2 & \text{Solve for x.}
\end{align*}
Try it
Solve [latex]5^{2x} = 25^{3x + 2}[/latex]
Example 3 Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base
Solve [latex]2^{5x} = \sqrt{2}[/latex].
Solution
\begin{align*}
2^{5x} &= 2^{\frac{1}{2}} & \text{Write the square root of 2 as a power of 2.}\\
5x & = \dfrac{1}{2} & \text{Use the one-to-one property.}\\
x &= \dfrac{1}{10} & \text{Solve for x.}
\end{align*}
Try it
Solve [latex]5^{x} = \sqrt{5}[/latex].
Q & A…
Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem solving process?
No. Recall that the range of an exponential function is always positive. While solving the equation, we may obtain an expression that is undefined.
Example 4 Solving an Equation with Positive and Negative Powers
Solve [latex]3^{x + 1} = -2[/latex].
Solution This equation has no solution. There is no real value of x that will make the equation a true statement because any power of a positive number is positive.
Analysis Figure 2 shows that the two graphs do not cross so the left side is never equal to the right side. Thus the equation has no solution.
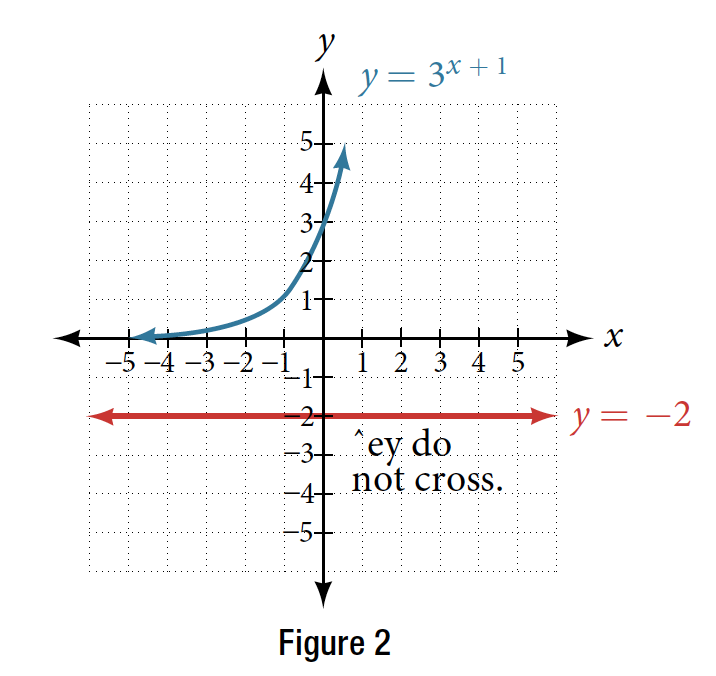
Try it
Solve [latex]2^{x} = -100[/latex].
Solving Exponential Equations Using Logarithms
Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since [latex]\log (a) = \log (b)[/latex] is equivalent to [latex]a = b[/latex], we may apply logarithms with the same base on both sides of an exponential equation.
How To…
Given an exponential equation in which a common base cannot be found, solve for the unknown.
- Apply the logarithm of both sides of the equation.
a. If one of the terms in the equation has base 10, use the common logarithm.
b. If none of the terms in the equation has base 10, use the natural logarithm. - Use the rules of logarithms to solve for the unknown.
Example 5 Solving an Equation Containing Powers of Different Bases
Solve [latex]5^{x + 2} = 4^{x}[/latex].
Solution
\begin{align*}
5^{x + 2} &= 4^{x} & \text{There is no easy way to get the powers to have the same base.}\\
\ln (5^{x + 2}) &= \ln (4^{x}) & \text{Take ln of both sides.}\\
(x + 2) \ln (5) &= x \ln (4) & \text{Use laws of logs.}\\
x \ln (5) + 2 \ln (5) &= x \ln (4) & \text{Use the distributive law.}\\
x \ln (5) − x \ln (4) &= −2 \ln (5) & \text{Get terms containing x on one side, terms without x on the other.}\\
x(\ln (5) − \ln (4)) &= −2 \ln (5) & \text{On the left hand side, factor out an x.}\\
x \ln \left(\dfrac{5}{4} \right) &= \ln \left(\dfrac{1}{25} \right) & \text{Use the laws of logs.}
x &= \dfrac{\ln \left(\dfrac{1}{25} \right)}{\ln \left(\dfrac{5}{4} \right)} & \text{Divide by the coefficient of x.}
\end{align*}
Try it
Solve [latex]2^{x} = 3^{x + 1}[/latex].
Q & A…
Is there any way to solve [latex]2^{x} = 3^{x}[/latex]?
Yes. The solution is [latex]0[/latex].
Equations Containing e
One common type of exponential equations are those with base e. This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base e on either side, we can use the natural logarithm to solve it.
How To…
Given an equation of the form [latex]y = Ae^{kt}[/latex], solve for [latex]t[/latex].
- Divide both sides of the equation by [latex]A[/latex].
- Apply the natural logarithm of both sides of the equation.
- Divide both sides of the equation by [latex]k[/latex].
Example 6 Solve an Equation of the Form [latex]\pmb{\textcolor{#ffffff}{y = Ae^{kt}}}[/latex]
Solve [latex]100 = 20e^{2t}[/latex].
Solution
\begin{align*}
100 &= 20e^{2t}\\
5 &= e^{2t} & \text{Divide by the coefficient of the power.}\\
\ln (5) &= 2t & \text{Take ln of both sides. Use the fact that ln(x) and e x are inverse functions.}\\
t &= \dfrac{\ln (5)}{2} & \text{Divide by the coefficient of t.}
\end{align*}
Analysis Using laws of logs, we can also write this answer in the form [latex]t = \ln \sqrt{5}[/latex]. If we want a decimal approximation of the answer, we use a calculator.
Try it
Solve [latex]3e^{0.5t} = 11[/latex].
Q & A…
Does every equation of the form [latex]\pmb{y = Ae^{kt}}[/latex] have a solution?
No. There is a solution when [latex]k \neq 0[/latex], and when y and A are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is [latex]2 = −3e^{t}[/latex].
Example 7 Solving an Equation That Can Be Simplified to the Form [latex]\pmb{\textcolor{#ffffff}{y = Ae^{kt}}}[/latex]
Solve [latex]4e^{2x} + 5 = 12[/latex].
Solution
\begin{align*}
4e^{2x} + 5 &= 12\\
4e^{2x} &= 7 & \text{Combine like terms.}\\
e^{2x} &= \dfrac{7}{4} & \text{Divide by the coefficient of the power.}\\
2x &= \ln \left(\dfrac{7}{4} \right) & \text{Take ln of both sides.}\\
x &= \dfrac{1}{2} \ln \left(\dfrac{7}{4} \right) & \text{Solve for x.}
\end{align*}
Try it
Solve [latex]3 + e^{2t} = 7e^{2t}[/latex].
Extraneous Solutions
Sometimes the methods used to solve an equation introduce an extraneous solution, which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.
Example 8 Solving Exponential Functions in Quadratic Form
Solve [latex]e^{2x} - e^{x} = 56[/latex].
Solution
\begin{align*}
e^{2x} – e^{x} &= 56\\
e^{2x} – e^{x} – 56 &= 0 & \text{Get one side of the equation equal to zero.}\\
(e^{x} + 7)(e^{x} – 8) &= 0 & \text{Factor by the FOIL method.}\\
e^{x} + 7 &= 0 \text{or} e^{x} – 8 = 0 & \text{If a product is zero, then one factor must be zero.}\\
e^{x} &= -7 \text{or} e^{x} = 8 & \text{Isolate the exponentials.}\\
e^{x} &= 8 & \text{Reject the equation in which the power equals a negative number.}\\
x &= \ln (8) & \text{Solve the equation in which the power equals a positive number.}
\end{align}*
Analysis When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation [latex]e^{x} = −7[/latex] because a positive number never equals a negative number. The solution [latex]\ln (−7)[/latex] is not a real number, and in the real number system this solution is rejected as an extraneous solution.
Try it
Solve [latex]e^{2x} = e^{x} + 2[/latex].
Q & A…
Does every logarithmic equation have a solution?
No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.
Using the Definition of a Logarithm to Solve Logarithmic Equations
We have already seen that every logarithmic equation [latex]\log_{b} (x) = y[/latex] is equivalent to the exponential equation [latex]b^{y} = x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation [latex]\log_{2} (2) + \log_{2} (3x − 5) = 3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x:
\begin{align*}
\log_{2} (2) + \log_{2} (3x − 5) &= 3\\
\log_{2} (2(3x – 5)) &= 3 & \text{Apply the product rule of logarithms.}\\
\log_{2} (6x – 10) &= 3 & \text{Distribute.}\\
2^{3} &= 6x – 10 & \text{Apply the definition of a logarithm.}\\
8 &= 6x – 10 & \text{Calculate } 2^{3}.\\
18 &= 6x & \text{Add 10 to both sides.}\\
x &= 3 & \text{Divide by 6.}
\end{align*}
using the definition of a logarithm to solve logarithmic equations
For any algebraic expression S and real numbers b and c, where [latex]b > 0, b \neq 1[/latex],
[latex]\log_{b} (S) = c \text{ if and only if } b^{c} = S[/latex]
Example 9 Using Algebra to Solve a Logarithmic Equation
Solve [latex]2 \ln (x) + 3 = 7[/latex].
Solution
\begin{align*}
2 \ln (x) + 3 &= 7\\
2 \ln (x) &= 4 & \text{Subtract 3.}\\
\ln (x) &= 2 & \text{Divide by 2.}\\
x &= e^{2} & \text{Rewrite in exponential form.}
\end{align*}
