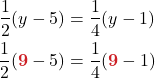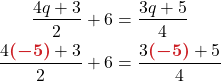7 Solve Linear Equations
Topics Covered:[1]
Solve Equations with Subtraction and Addition Property of Equality
We are going to use a model to clarify the process of solving an equation. An envelope represents the variable – since its contents are unknown – and each counter represents one. We will set out one envelope and some counters on our workspace, as shown below. Both sides of the workspace have the same number of counters, but some counters are “hidden” in the envelope. Can you tell how many counters are in the envelope?
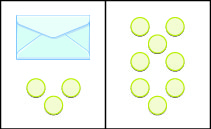
What are you thinking? What steps are you taking in your mind to figure out how many counters are in the envelope?
Perhaps you are thinking: “I need to remove the 3 counters at the bottom left to get the envelope by itself. The 3 counters on the left can be matched with 3 on the right and so I can take them away from both sides. That leaves five on the right—so there must be 5 counters in the envelope.” See below for an illustration of this process.
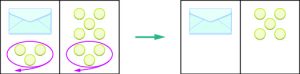
What algebraic equation would match this situation? In the image below each side of the workspace represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope x.
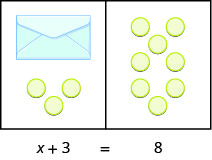
| Steps | Algebraic |
| Equation | |
| First, we took away three from each side. | |
| Then we were left with five. | |
|
Check: |
Five in the envelope plus three more does equal eight! 5 + 3 = 8
|
Subtraction Property of Equality
For any numbers a, b, and c:
If a = b, then a − c = b − c.
When you subtract the same quantity from both sides of an equation, you still have equality.
Let’s see how to use this property to solve an equation. Remember, the goal is to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.
Try it!
Solve: y + 37 = −13
Solution (click to reveal)
To get y by itself, we will undo the addition of 37 by using the Subtraction Property of Equality.
| Steps | Algebraic |
| Equation | |
| Subtract 37 from each side to ‘undo’ the addition. | |
| Simplify. | |
| Check: | |
| Substitute y = −50 | |
| Simplify and compare |
Since y = -50 makes y + 37 = -13 a true statement, we have the solution to this equation.
Addition Property of Equality
For any numbers a, b, and c:
If a = b, then a + c = b + c
When you add the same quantity to both sides of an equation, you still have equality.
In the try it exercise above, 37 was added to the y and so we subtracted 37 to ‘undo’ the addition. In the problem below, we will need to ‘undo’ subtraction by using the Addition Property of Equality.
Try it!
Solve: a − 28 = −37.
Solution (click to reveal)
| Steps | Algebraic |
| Equation | |
| Add 28 to each side to ‘undo’ the subtraction. | |
| Simplify. | |
| Check: | |
| Substitute a = −9 | |
| Simplify and compare |
The solution to a − 28 = −37 is a =−9.
Solve: ![]()
Solution (click to reveal)
| Steps | Algebraic |
| Equation | |
| Use the Addition Property of Equality. | |
| Find the LCD to add the fractions on the right. | |
| Simplify. | |
| Check: | |
| Substitute |
|
| Subtract. | |
| Simplify. |
The solution to ![]() is
is ![]() .
.
The next example will be an equation with decimals.
Solve: n − 0.63 = −4.2.
Solution (click to reveal)
| Steps | Algebraic |
| Equation | |
| Use the Addition Property of Equality. | |
| Simplify | |
| Check: | |
| Let |
|
| Simplify and compare |
The solution to ![]() is
is ![]() .
.
Solve Equations with Multiplication and Division Property of Equality
You may have noticed that all of the equations we have solved so far have been of the form x + a = b or x − a = b. We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.
Let’s look at our puzzle again with the envelopes and counters in the image.
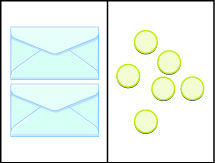
In the illustration, there are two identical envelopes that contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
How do we determine the number? We have to separate the counters on the right side into two groups of the same size to correspond with the two envelopes on the left side. The 6 counters divided into 2 equal groups gives 3 counters in each group (since 6 ÷ 2 = 3).
What equation models the situation shown in the image? There are two envelopes, and each contains x counters. Together, the two envelopes must contain a total of 6 counters.
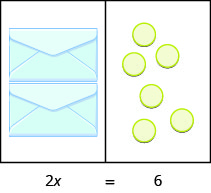
| Steps | Algebraic |
| Equation | |
| If we divide both sides of the equation by 2, as we did with the envelopes and counters, | |
| we get: |
We found that each envelope contains 3 counters. Does this check? We know 2 · 3 = 6, so it works! Three counters in each of two envelopes does equal six!
This example leads to the Division Property of Equality.
The Division Property of Equality
For any numbers a, b, and c, and c ≠ 0,
When you divide both sides of an equation by any non-zero number, you still have equality.
The goal in solving an equation is to ‘undo’ the operation on the variable. In the next example, the variable is multiplied by 5, so we will divide both sides by 5 to ‘undo’ the multiplication.
Try it!
Solve: 5x = −27
Solution (click to reveal)
| Steps | Algebraic |
| To isolate x, “undo” the multiplication by 5. | |
| Divide to ‘undo’ the multiplication. | |
| Simplify. | |
| Check: | |
| Substitute |
|
| Simplify and compare | |
| Solution | Since this is a true statement, |
Consider the equation ![]() . We want to know what number divided by 4 gives 3. So to “undo” the division, we will need to multiply by 4. The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
. We want to know what number divided by 4 gives 3. So to “undo” the division, we will need to multiply by 4. The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
The Multiplication Property of Equality
For any numbers a, b, and c,
If you multiply both sides of an equation by the same number, you still have equality.
Try it!
Solve: ![]() .
.
Solution (click to reveal)
Here y is divided by −7. We must multiply by −7 to isolate y.
| Steps | Algebraic |
| Equation | |
| Multiply both sides by −7. | |
| Multiply. | |
| Simplify. | |
| Check: | |
| Substitute |
|
| Divide. |
Solve: ![]() .
.
Solution C (click to reveal)
Since the product of a number and its reciprocal is 1, our strategy will be to isolate x by multiplying by the reciprocal of ![]() .
.
| Steps | Algebraic |
| Equation | |
| Multiply by the reciprocal of |
|
| Reciprocals multiply to 1. | |
| Multiply. | |
| Side Note: | Notice that we could have divided both sides of the equation While this would work, most people would find multiplying by the reciprocal easier. |
| Check: | |
| Substitute x = 16 | |
| Simplify and compare | 12 = 12 ✓ |
|
Subtraction Property |
Addition Property |
Division Property | Multiplication Property |
| For any numbers a, b, and c:
If a = b, then a − c = b − c. When you subtract the same quantity from both sides of an equation, you still have equality. |
For any numbers a, b, and c: If a = b, then a + c = b + c When you add the same quantity to both sides of an equation, you still have equality. |
For any numbers a, b, and c, and c ≠ 0: If a = b, then When you divide both sides of an equation by any non-zero number, you still have equality. |
For any numbers a, b, and c, If a = b, then ac = bc If you multiply both sides of an equation by the same number, you still have equality. |
When you add, subtract, multiply, or divide the same quantity from both sides of an equation, you still have equality
Solve Linear Equations Using a General Strategy
Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that makes it a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle!
Solution of an Equation
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
The solution set consists of all values that make the equation true.
To determine whether a number is a solution to an equation, we substitute the value for the variable in the equation. If the resulting equation is a true statement, then the number is a solution of the equation.
- Substitute the number for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
Try it!
Determine whether the values are solutions to the equation 5y + 3 = 10y − 4.
a. ![]() b.
b. ![]()
Solution A (click to reveal)
Since a solution to an equation is a value of the variable that makes the equation true, begin by substituting the value of the solution for the variable.
a.
| Steps | Algebraic |
| Equation | |
| Substitute |
|
| Multiply. | |
| Simplify. |
Since ![]() does not result in a true equation,
does not result in a true equation, ![]() is not a solution to the equation 5y + 3 = 10y − 4.
is not a solution to the equation 5y + 3 = 10y − 4.
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Equation | |
| Substitute |
|
| Multiply. | |
| Simplify. |
Since ![]() results in a true equation,
results in a true equation, ![]() is a solution to the equation 5y + 3 = 10y − 4.
is a solution to the equation 5y + 3 = 10y − 4.
There are many types of equations that we will learn to solve. In this section we will focus on a linear equation.
Linear Equations
A linear equation is an equation in one variable that can be written, where a and b are real numbers and a ≠ 0, as:
ax + b = 0
To solve a linear equation it is a good idea to have an overall strategy that can be used to solve any linear equation. In the next example, we will give the steps of a general strategy for solving any linear equation. Simplifying each side of the equation as much as possible first makes the rest of the steps easier.
How to solve a linear equation using a general strategy
- Simplify each side of the equation as much as possible. Use the Distributive Property to remove any parentheses. Combine like terms.
- Collect all the variable terms on one side of the equation. Use the Addition or Subtraction Property of Equality.
- Collect all the constant terms on the other side of the equation. Use the Addition or Subtraction Property of Equality.
- Make the coefficient of the variable term equal to 1. Use the Multiplication or Division Property of Equality. State the solution to the equation.
- Check the solution.
Substitute the solution into the original equation to make sure the result is a true statement.
Try it!
Solve: 7(n − 3) − 8 = −15.
Solution (click to reveal)
| Steps | Algebraic |
| Step 1. Simplify each side of the equation as much as possible. |
|
| Step 2. Collect all variable terms on one side of the equation. |
|
| Step 3. Divide both side by 7. |
|
| Step 4. Check the solution. |
|
We can solve equations by getting all the variable terms to either side of the equal sign. By collecting the variable terms on the side where the coefficient of the variable is larger, we avoid working with some negatives. This will be a good strategy when we solve inequalities later in this chapter. It also helps us prevent errors with negatives.
Try it!
Solve: 4(x − 1) − 2 = 5(2x + 3) + 6.
Solution (click to reveal)
| Steps | Algebraic |
| Original Problem | |
| Distribute. | |
| Combine like terms. | |
| Subtract 4x from each side to get the variables only on the right since 10 > 4. | |
| Simplify. | |
| Subtract 21 from each side to get the constants on left. | |
| Simplify. | |
| Divide both sides by 6. | |
| Simplify. | |
| Check:
Substitute
|
|
Solve: 10[3 − 8(2s − 5)] = 15(40 − 5s).
Solution (click to reveal)
| Steps | Algebraic |
| Equation: | |
| Simplify from the innermost parentheses first. | |
| Combine like terms in the brackets. | |
| Distribute. | |
| Add 160s to both sides. | |
| Simplify. | |
| Subtract 600 from both sides. | |
| Simplify. | |
| Divide both sides by 85. | |
| Simplify. | |
| Check:
Substitute
|
|
Solve Equations with Fractions
We could use the General Strategy to solve the next example. This method would work fine, but many students do not feel very confident when they see all those fractions. So, we are going to show an alternate method to solve equations with fractions. This alternate method eliminates the fractions.
We will apply the Multiplication Property of Equality and multiply both sides of an equation by the least common denominator (LCD) of all the fractions in the equation. The result of this operation will be a new equation, equivalent to the first, but without fractions. This process is called clearing the equation of fractions.
How to solve equations with fractions or decimal coefficients
- Find the least common denominator (LCD) of all the fractions and decimals (in fraction form) in the equation.
- Multiply both sides of the equation by that LCD. This clears the fractions and decimals.
- Solve using the General Strategy for Solving Linear Equations.
Try it!
Solve: ![]() .
.
Solution (click to reveal)
Find
| Steps | Algebraic |
| Find the LCD of
|
|
|
Multiply both sides of the equation by the LCD, 12.
|
|
| Use the Distributive Property. | |
| Simplify — and notice no more fractions! | |
| Subtract 10 from both sides. | |
| Simplify | |
| Check:
Substitute
|
|
Notice in the previous example, once we cleared the equation of fractions, the equation was like those we solved earlier in this chapter. We changed the problem to one we already knew how to solve. We then used the General Strategy for Solving Linear Equations.
Try it!
Solve: ![]() .
.
Solution (click to reveal)
| Steps | Algebraic |
| Equation | |
| Distribute. | |
| Simplify. | |
| Multiply by the LCD, four. | |
| Distribute. | |
| Simplify. | |
| Collect the variables to the left. | |
| Simplify. | |
| Collect the constants to the right. | |
| Simplify. |
An alternate way to solve this equation is to clear the fractions without distributing first. If you multiply the factors correctly, this method will be easier.
| Steps | Algebraic |
| Equation | |
| Multiply by the LCD, 4. | |
| Multiply four times the fractions. | |
| Distribute. | |
| Collect the variables to the left. | |
| Simplify. | |
| Collect the constants to the right. | |
| Simplify. | |
| Check:
Substitute
|
Finish the check on your own. |
When you multiply both sides of an equation by the LCD of the fractions, make sure you multiply each term by the LCD—even if it does not contain a fraction.
Try it!
Solve: ![]()
Solution (click to reveal)
| Steps | Algebraic | |
| Equation | ||
| Multiply both sides by the LCD, 4. | ||
| Distribute. | ||
| Simplify. | ||
| Distribute | ||
| Combine like terms | ||
| Collect the variables to the left. | ||
| Simplify. | ||
| Collect the constants to the right. | ||
| Simplify. | ||
| Divide both sides by five. | ||
| Simplify. | ||
| Check:
Substitute
|
Finish the check on your own. |
|
Classify Equations
Whether or not an equation is true depends on the value of the variable. The equation 7x + 8 = −13 is true when we replace the variable, x, with the value −3, but not true when we replace x with any other value. An equation like this is called a conditional equation.
An equation that is true for one or more values of the variable and false for all other values of the variable is a conditional equation.
For example, if we are to solve the equation 5x + 2 = 3x − 6, we have the following:
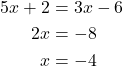
The solution set consists of one number: {−4}. It is the only solution and, therefore, we have solved a conditional equation.
Now let’s consider the equation 7y + 14 = 7(y + 2). Do you recognize that the left side and the right side are equivalent? Let’s see what happens when we solve for y.
Solve:
| Steps | Algebraic |
| Equation | 7y + 14 = 7(y + 2) |
| Distribute. | 7y + 14 = 7y + 14 |
| Subtract 7y to each side to get the y’s to one side. | |
| 4Simplify—the y’s are eliminated. | 14 = 14 |
| Compare | But 14 = 14 is true. |
This means that the equation 7y + 14 = 7(y + 2) is true for any value of y. We say the solution to the equation is all of the real numbers. An equation that is true for any value of the variable is called an identity.
An equation that is true for any value of the variable is called an identity.
The solution of an identity is all real numbers.
What happens when we solve the equation −8z = −8z + 9?
| Steps | Algebraic |
| Equation | −8z = −8z + 9 |
| Add 8z to both sides to leave the constant alone on the right. | |
| Simplify—the z’s are eliminated. | 0 ≠ 9 |
Solving the equation −8z = −8z + 9 led to the false statement 0 = 9. The equation -8z = −8z + 9 will not be true for any value of z. It has no solution. An equation that has no solution, or that is false for all values of the variable, is called a Inconsistent.
An equation that is false for all values of the variable is called an Inconsistent.
An Inconsistent Equation has no solution.
For example, if we are to solve 5x − 15 = 5(x − 4), we have the following:
| Steps | Algebraic |
| Equation | 5x − 15 = 5x − 20 |
| Subtract 5x from both sides. | 5x − 15 − 5x = 5x − 20 − 5x |
| False statement | −15 ≠ −20 |
Indeed, -15 ≠ −20. There is no solution because this is an inconsistent equation.
The next few examples will ask us to classify an equation as conditional, an identity, or as inconsistent.
Try it!
Classify the equation as a conditional equation, an identity, or inconsistent and then state the solution: 6(2n − 1) + 3 = 2n − 8 + 5(2n + 1).
Solution (click to reveal)
| Steps | Algebraic |
| Equation | 6(2n − 1) + 3 = 2n − 8 + 5(2n + 1) |
| Distribute. | 12n – 6 + 3 = 2n – 8 + 10n + 5 |
| Combine like terms. | 12n – 3 = 12n – 3 |
| Subtract 12n from each side to get the n’s to one side. | |
| Simplify. | -3 = -3 |
| This is a true statement. | The equation is an identity. |
| Solution | The solution is all real numbers. |
Classify the equation as a conditional equation, an identity, or a inconsistent and then state the solution:
8 + 3(a − 4) = 0.
Solution (click to reveal)
| Steps | Algebraic |
| Equation | 8 + 3(a − 4) = 0 |
| Distribute. | 8 +3a – 12 = 0 |
| Combine like terms. | 3a – 4 = 0 |
| Add 4 to both sides. | |
| Simplify. | 3a = 4 |
| Divide. | |
| Simplify. | a = |
| The equation is true when a= |
This is a conditional equation. |
| Solution | The solution is a = |
Classify the equation as a conditional equation, an identity, or inconsistent and then state the solution:
5m + 3(9 + 3m) = 2(7m − 11).
Solution (click to reveal)
| Steps | Algebraic |
| Equation | 5m + 3(9 + 3m) = 2(7m − 11) |
| Distribute. | 5m + 27 + 9m = 14m – 22 |
| Combine like terms. | 14m + 27 = 14m – 22 |
| Subtract 14m from both sides. | |
| Simplify. | 27 ≠ −22. |
| But 27 ≠ −22. | The equation is a inconsistent. |
| Solution | It has no solution. |
We summarize the methods for classifying equations in the table.
| Type of equation | What happens when you solve it? | Solution |
|---|---|---|
| Conditional Equation | True for one or more values of the variables and false for all other values | One or more values |
| Identity | True for any value of the variable | All real numbers |
| Inconsistent | False for all values of the variable | No solution |
Key Concepts
- How to determine whether a number is a solution to an equation
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true.
If it is true, the number is a solution.
If it is not true, the number is not a solution.
- How to Solve Linear Equations Using a General Strategy
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution.
Substitute the solution into the original equation to make sure the result is a true statement.
- Simplify each side of the equation as much as possible.
- How to Solve Equations with Fraction or Decimal Coefficients
- Find the least common denominator (LCD) of all the fractions and decimals (in fraction form) in the equation.
- Multiply both sides of the equation by that LCD. This clears the fractions and decimals.
- Solve using the General Strategy for Solving Linear Equations.
- Derived from Openstax Intermediate Algebra; Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction. & College Algebra 2e with Corequisite Supports, Access for free at https://openstax.org/books/college-algebra-corequisite-support-2e/pages/1-introduction-to-prerequisites ↵

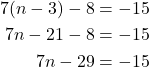
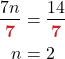
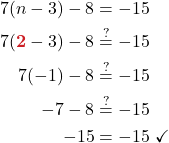
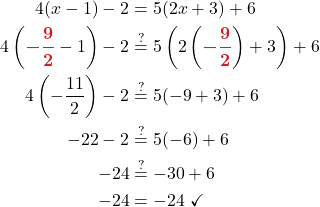
![Rendered by QuickLaTeX.com \begin{align*} \displaystyle 10[3 - 8(2s - 5)] &= 15(40 - 5s)\\ \displaystyle 10[3 - 8(2({\color{myred1} \boldsymbol{-2}}) - 5)] &\stackrel{?}{=} 15(40 - 5({\color{myred1} \boldsymbol{-2}}))\\ 10[3 - 8(-4 - 5)] &\stackrel{?}{=} 15(40 + 10)\\ 10[3 - 8(-9)] &\stackrel{?}{=} 15(50)\\ 10(3 + 72) &\stackrel{?}{=} 750\\ 10(75) &\stackrel{?}{=} 750\\ 750 &= 750 \ \checkmark \end{align*}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7aa6de178f8f2ff81e53a00397471538_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \frac{1}{12}x + \frac{5}{6} &= \frac{3}{4}\\[0.1cm] \textbf{LCD} &= 12 \end{align*}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d2f89116c1e4fc48ffcf9139ad7c509e_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \frac{1}{12}x + \frac{5}{6} &= \frac{3}{4}\\[0.1cm] \frac{1}{12}{\color{myred1} \boldsymbol{(-1)}} + \frac{5}{6} &\stackrel{?}{=} \frac{3}{4}\\[0.1cm] -\frac{1}{12} + \frac{5}{6} &\stackrel{?}{=} \frac{3}{4}\\[0.1cm] -\frac{1}{12} + \frac{10}{12} &\stackrel{?}{=} \frac{9}{12}\\[0.1cm] \frac{9}{12} &= \frac{9}{12} \ \checkmark \end{align*}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4a235b25020abf136ff838aa420e035e_l3.png)