"

11 Inequalities

Topics Covered

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
  1. Graph Inequalities on a Number Line
  2. Solve Linear Inequalities
  3. Compound Inequalities
  4. Solve Applications with Linear Inequalities
  5. Key Concepts

Graph Inequalities on a Number Line

What number would make the inequality x > 3 true? Are you thinking, “x could be four”? That’s correct, but x could be 6, too, or 37, or even 3.001. Any number greater than three is a solution to the inequality x > 3.

Indicating the solution to an inequality can be achieved in several ways.

  • We show all the solutions to the inequality x > 3 on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three. The image below shows the number line.
  • We can also represent inequalities usinginterval notation, in which solution sets are indicated with parentheses or brackets. There is no upper end to the solution to this inequality. In interval notation, we express x > 3 as (3, ∞). The symbol∞ is read as “infinity.” It is not an actual number.
  • We can use set-builder notation: {x|x > 3}, which translates to “all real numbers x such that x is greater than 3.” Notice that braces are used to indicate a set.
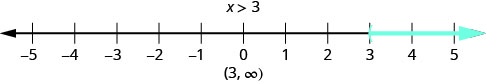
The figure shows the inquality, x is greater than 3, graphed on a number line from negative 5 to 5. There is shading that starts at 3 and extends to numbers to its right. The solution for the inequality is written in interval notation. It is the interval from 3 to infinity, not including 3.
The inequality x > 3 is graphed on this number line and written in interval notation.
How to write in interval notation.
  • The smallest number from the interval is written first.
  • The largest number in the interval is written second, following a comma.
  • Parentheses, ( or ), are used to signify that an endpoint value is not included, called exclusive.
  • Brackets, [ or ], are used to indicate that an endpoint value is included, called inclusive.

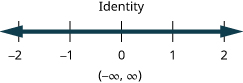
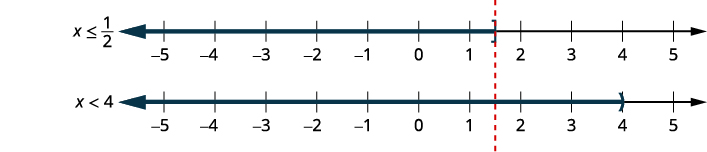
The inequality  x ≤ 1 means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at x = 1. We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions.

There is no lower end to those numbers. We write x ≤ 1 in interval notation as (−∞, 1]. The symbol −∞ is read as “negative infinity.” The image below shows both the number line and interval notation.

The figure shows the inquality, x is less than or equal to l, graphed on a number line from negative 5 to 5. There is shading that starts at 1 and extends to numbers to its left. The solution for the inequality is written in interval notation. It is the interval from negative infinity to one, including 1.
The inequality x ≤ 1 is graphed on this number line and written in interval notation.

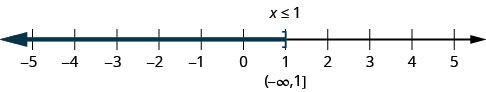
The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals.

Inequalities, Number Lines, and Interval Notation
The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.”

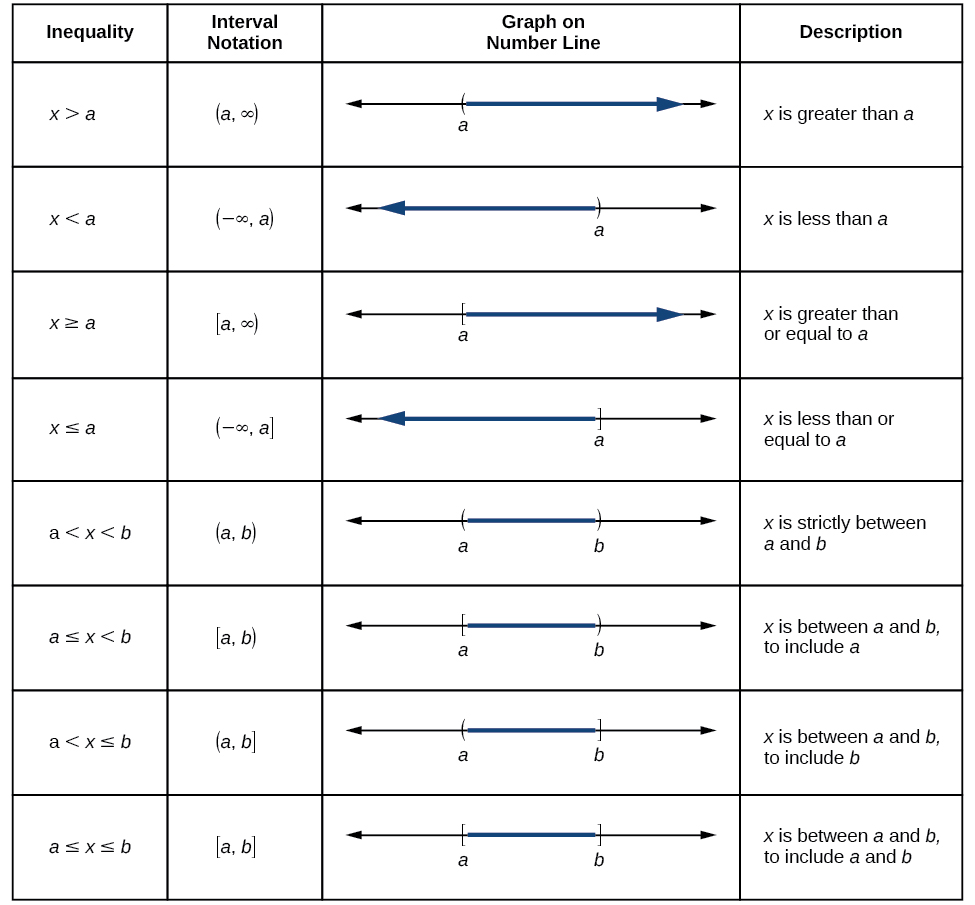
A few examples of an interval, or a set of numbers in which a solution falls, are [−2, 6), or all numbers between −2 and 6, including –2, but not including 6; (−1, 0), all real numbers between, but not including −1 and 0; and (−∞, 1], all real numbers less than and including 1. This is summarized below.

Summary of interval notation.

First, we will look at interval notation with inequalities. We will return to the set-builder format in a little bit.

Try it! – Using Interval Notation to Express All Real Numbers Greater Than or Equal to a

  1. Use interval notation to indicate all real numbers greater than or equal to −2.

Solution

Use a bracket on the left of −2 and parentheses after infinity: [−2, ∞). The bracket indicates that −2 is included in the set with all real numbers greater than −2 to infinity.

2.  Graph each inequality on the number line and write in interval notation.

a. x ≥ −3     b. x < 2.5    c. \displaystyle x\leq -\frac{3}{5}

Solution

a.

Steps Algebraic
x greater than or equal to -3
Shade to the right of −3, and put a bracket at −3. Shade to the right of negative 3 and put a left bracket at negative 3. The solution of the inequality x is greater than negative 3 is indicated on a number line with a left bracket at a and shading to the right. Write in intervak notation. The solution in interval notation is the interval from negative 3 to infinity enclosed within a left bracket and right parenthesis.
Write in interval notation. [-3, infinity)

b.

Steps Algebraic
x less than 2.5
Shade to the left of 2.5 and put a parenthesis at 2.5. Shade to the left of negative 2.5 and put a parenthesis at negative 2.5. The solution of the inequality x is less than 2.5 is indicated on a number line with a right bracket at 2.5 and shading to the left. Write in interval notation. The solution in interval notation is the interval from negative infinity to 2.5 enclosed within parentheses.
Write in interval notation. (negative infinity, 2.5)

c.

Steps Algebraic
x greater than or equal to negative 3 over 5
Shade to the left of −35 and put a bracket at −35. Shade to the left of negative three-fifths and put a right bracket at negative three-fifths. The solution of the inequality x is less than or equal to negative three-fifths is indicated on a number line with a right bracket at negative three-fifths and shading to the left.
Write in interval notation. Write in interval notation. The solution in interval notation is the interval from negative infinity to negative three-fifths enclosed within a left parentheses and right bracket.

What numbers are greater than two but less than five? Are you thinking say, 2.5, 3, 3\frac{2}{3}, 4, 99? We can represent all the numbers between two and five with the inequality 2 < x < 5. We can show 2 < x < 5 on the number line by shading all the numbers between two and five. Again, we use the parentheses to show the numbers two and five are not included.The graph of the inequality 2 is less than x which is less than 5 shows open circles a 2 and 5 and shading in between.

Try it!

Graph each inequality on the number line and write in interval notation.

a. −3 < x < 4     b. −6 ≤ x < −1     c. 0 ≤ x ≤ 2.5

Solution

a.

Steps Algebraic
Negative 3 is less than x which is less than 4.
Shade between −3 and 4.

Put a parenthesis at −3 and 4.		 There open circles at negative 3 and 4 and shading between negative 3 and 4 on the number line. Put parenthese at negative 3 and 4. Write in interval notation.
Write in interval notation. (-3.4)

b.

Steps Algebraic
Negative 6 is less than or equal to x which is less than negative 1.
Shade between −6 and −1.

Put a bracket at −6, and a parenthesis at −1.		 There is closed circle at negative 6 and an open circle at negative 1 and shading between negative 6 and negative 1 on the number line. Put a bracket at negative 6 and a parenthesis at 1.
Write in interval notation. [-6,1)

c.

Steps Algebraic
0 is less than or equal to x which is less than or equal to 2.5.
Shade between 0 and 2.5.
Put a bracket at 0 and at 2.5.		 There are closed circles at 0 and 2.5 and shading between negative 0 and 2.5 on the number line. Put brackets at 0 and 2.5.
Write in interval notation. [0,2.5]

This format changes slightly in set-builder notation. For example, {x|10 ≤ x < 30} describes the behavior of x in set-builder notation. The braces { } are read as “the set of,” and the vertical bar | is read as “such that,” so we would read {x|10 ≤ x < 30} as “the set of x-values such that 10 is less than or equal to x, and x is less than 30.”

The table compares inequality notation, set-builder notation, and interval notation.

Set Indicated Set-Builder Notation Interval Notation
All real numbers between a and b, but not including a or b {x|a < x < b} (a, b)
All real numbers greater than a, but not including a {x|x > a} (a, ∞)
All real numbers less than b, but not including b {x|x <  b} (−∞, b)
All real numbers greater than a, including a {x|x ≥ a} [a, ∞)
All real numbers less than b, including b {x|x ≤ b} (−∞, b]
All real numbers between a and b, including a {x|a ≤ x < b} [a, b)
All real numbers between a and b, including b {x|a < x ≤ b} (a, b]
All real numbers between a and b, including a and b {x|a ≤ x ≤ b} [a, b]
All real numbers less than a or greater than b {x|x < a or x > b} (−∞, a) ∪ (b, ∞)
All real numbers {x|x is a real number} (−∞, ∞)

So, what about when you have two sets of intervals that you need to graph? To combine two intervals using inequality notation or set-builder notation, we use the word “or,” and we use the union symbol, ∪, to combine two unconnected intervals. For example, the union of the sets {2, 3, 5} and {4, 6} is the set {2, 3, 4, 5, 6}. It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is

{x||x| ≥ 3} = (−∞, −3] ∪ [3, ∞)

Try it! – Describing Sets on the Real-Number Line

Describe the intervals of values shown below using inequality notation, set-builder notation, and interval notation.

<img class=”size-full wp-image-2354 aligncenter” src=”https://utsa.pressbooks.pub/app/uploads/sites/143/2025/03/CNX_Precalc_Figure_01_02_004.jpg” alt=”Line graph of 1<=x

Solution

To describe the values, x, included in the intervals shown, we would say, “x is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”

Steps Algebraic
Inequality 1 ≤ x ≤ 3 or x > 5
Set-builder notation {x|1 ≤ x ≤ 3 or x > 5}
Interval notation [1, 3] ∪ (5, ∞)

Remember that, when writing or reading interval notation, using a square bracket means the boundary is included in the set. Using a parenthesis means the boundary is not included in the set.

Solve Linear Inequalities

A linear inequality is much like a linear equation—but the equal sign is replaced with an inequality sign. A linear inequality is an inequality in one variable that can be written in one of the forms,

Ex. 1  Ex. 2 Ex. 3 Ex. 4
ax + b < c, ax + b ≤ c, ax+ b > c, ax+ b ≥ c.

Linear Inequality

A linear inequality is an inequality in one variable that can be written in one of the following forms where a, b, and c are real numbers and a ≠ 0:

4 Forms of an inequality ax + b < c, ax + b ≤ c, ax+ b > c, ax+ b ≥ c.

When we solved linear equations, we were able to use the properties of equality to add, subtract, multiply, or divide both sides and still keep the equality. Similar properties hold true for inequalities.

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality. For example:

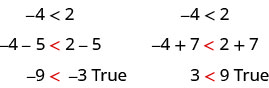
Negative 4 is less than 2. Negative 4 minus 5 is less than 2 minus 5. Negative 9 is less than negative 3, which is true. Negative 4 is less than 2. Negative 4 plus 7 is less than 2 plus 7. 3 is less than 9, which is true.
Notice that the inequality sign stayed the same.

This leads us to the Addition and Subtraction Properties of Inequality.

Addition and Subtraction Property of Inequality

For any numbers a, b, and c, if a < b, then

Addition Property Subtraction Property
a + c < b + c a − c < b − c
a + c > b + c a − c > b − c

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality.

What happens to an inequality when we divide or multiply both sides by a constant?

Let’s first multiply and divide both sides by a positive number.


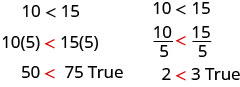10 is less than 15. 10 times 5 is less than 15 times 5. 50 is less than 75 is true. 10 is less than 15. 10 divided by 5 is less than 15 divided by 5. 2 is less than 3 is true.The inequality signs stayed the same.

Does the inequality stay the same when we divide or multiply by a negative number?

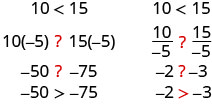10 is less than 15 10 times negative 5 is blank 15 times negative 5? Negative 50 is blank negative 75. Negative 50 is greater than negative 75. 10 is less than 15. 10 divided by negative 5 is blank 15 divided by negative 5. Negative 2 is blank negative 3. Negative 2 is blank negative 3.Notice that when we filled in the inequality signs, the inequality signs reversed their direction.

When we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses.

Multiplication and Division Property of Inequality

For any numbers a, b, and c:

Multiplication and Division Property, if multiply/divide by a Positive number Multiplication and Division Property, if multiply/divide by a Negative number
if a < b and c > 0 ,then ac < bc and \displaystyle\frac{a}{c}  <  \displaystyle\frac{b}{c}. if a > b and c > 0, then ac > bc and \displaystyle\frac{a}{c}  >  \displaystyle\frac{b}{c}.
if a < b and c < 0, then ac > bc and \displaystyle\frac{a}{c}  >  \displaystyle\frac{b}{c}. if a > b and c < 0, then ac < bc and \displaystyle\frac{a}{c}  <  \displaystyle\frac{b}{c}.

When we divide or multiply an inequality by a:

  • positive number, the inequality stays the same.
  • negative number, the inequality reverses.

Sometimes when solving an inequality, as in the next example, the variable ends upon the right. We can rewrite the inequality in reverse to get the variable to the left.

x > a has the same meaning as a < x

Think about it as “If Xander is taller than Andy, then Andy is shorter than Xander.”

Try it!

Solve each inequality. Graph the solution on the number line, and write the solution in interval notation.

a. \displaystyle x-\frac{3}{8}\leq\frac{3}{4}     b. 9y < ​​54     c. \displaystyle -15<\frac{3}{5}z

Solution

a.

Steps Algebraic
Inequality
x minus three-eighths plus three-eighths is less than or equal to three-fourths.
Add  \displaystyle\frac{3}{8}  to both sides of the inequality.
x minus three-eighths plus three-eighths is less than or equal to three-fourths plus three-eighths.
Simplify.
Simplify. x is less than nine-eighths.
Graph the solution on the number line.
Graph the solution on a number line with a right bracket at nine-eighths with shading to the left.
Write the solution in interval notation.
Write the solution, negative infinity to nine-eighths, within a parenthesis and bracket.

b.

Steps Algebraic
Inequality
9 y is less than 54.
Divide both sides of the inequality by 9; since  
9 is positive, the inequality stays the same.
Divide both sides of the inequality by 9. Because 9 is less than 0, the inequality stays the same. 9 y divided by 9 is less than 54 divided by 9.
Simplify.
Simplify. y is less than 6.
Graph the solution on the number line.
Graph the solution on the number line with a right parenthesis at 6 with shading to the left.
Write the solution in interval notation.
Write the solution, negative infinity to 6, within parentheses.

c.

Steps Algebraic
Inequality
Negative 15 is less than three-fifths z .
Multiply both sides of the inequality by \displaystyle\frac{5}{3}
Since \displaystyle\frac{5}{3} is positive, the inequality stays the same.
Multiply both sides of the inequality by five-thirds. Five-thirds times negative 15 is less than five-thirds times three-fifths z. Since five-thirds is greater than 0, the inequality stays the same.
Simplify.
Simplify. Negative 25 is less than z.
Rewrite with the variable on the left.
. Rewrite with the variable on the left. Z is greater than negative 25.
Graph the solution on the number line.
Graph the solution on the number line with a left parenthesis at negative 25 with shading to the right.
Write the solution in interval notation.
Write the solution in interval notation. It is negative 25 to infinity within parentheses.

Be careful when you multiply or divide by a negative number—remember to reverse the inequality sign.

Try it!

Solve each inequality, graph the solution on the number line, and write the solution in interval notation.

a. \displaystyle -13m\geq 65    b. \displaystyle\frac{n}{-2}\geq 8

Solution

a.

Steps Algebraic
Inequality
Negative 13 m is greater than or equal to 65.
Divide both sides of the inequality by −13.

Since −13 is a negative, the inequality reverses.
Divided both sides of the inequality by negative 13. Negative 13 m divided y negative 13 is less than or equal to 65 divided by negative 13. Since negative 13 is less than 0, the inequality reverses.
Simplify.
Simplify. m is less than or equal to negative 5.
Graph the solution on the number line.
Graph the solution on the number line with a right bracket at negative 5 with shading to the left.
Write the solution in interval notation.
Write the solution in interval notation. It is negative infinity to negative 5 within a parenthesis and bracket.

b.

Steps Algebraic
Inequality
n divided by negative 2 is greater than or equal to 8.
Multiply both sides of the inequality by −2.

Since −2 is a negative, the inequality reverses.
Multiply both sides of the inequality by negative 2. Negative times the quantity n divided by negative 2 is less thann or equal to negative 2 times 8 Since negative 2 is less than 0, the inequality reverses.
Simplify.
Simplify. n is less than or equal to negative 16.
Graph the solution on the number line.
Graph the solution on the number line with a right bracket at negative 16 with shading to the left.
Write the solution in interval notation.
Write the solution in interval notation. It is negative infinity to negative 16 within a parenthesis and bracket.

Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but make sure to pay close attention when we multiply or divide to isolate the variable.

Try it!

Solve the inequality 6y ≤ 11y + 17, graph the solution on the number line, and write the solution in interval notation.

Solution

Steps Algebraic
Inequality
6 y is less than or equal to 11 y plus 17.
Subtract 11y from both sides to collect the variables on the left.
Subtract 11 y from both sides to collect the variables on the left. 6 y minus 11 y is less than or equal to 11 y minus 11 y plus 17.
Simplify.
Simplify. Negative 5 y is less than or equal to 17.
Divide both sides of the inequality by −5 and reverse the inequality.
Divide both sides of the inequality by negative 5 and reverse the inequality. Negative 5 y is less than negative 5 is greater than or equal to 17 divided by negative 5.
Simplify.
Simplify. y is greater than or equal to 17 divided by negative 5.
Graph the solution on the number line.
Graph the solution on the number line with a left bracket at negative 17 divided by 5 with shading to the right.
Write the solution in interval notation.
Write the solution in interval notation. It is negative 17 divided by 5 to infinity within brackets.

When solving inequalities, it is usually easiest to collect the variables on the side where the coefficient of the variable is largest. This eliminates negative coefficients and so we don’t have to multiply or divide by a negative—which means we don’t have to remember to reverse the inequality sign.

Try it!

Solve the inequality 8p +3(p − 12) > 7p − 28, graph the solution on the number line, and write the solution in interval notation.

Solution

Steps Algebraic
Inequality 8p + 3(p − 12) > 7p − 28
Simplify each side as much as possible.
Distribute. 8p + 3p − 36 > 7p − 28
Combine like terms. 11p − 36 > 7p − 28
Subtract 7p from both sides to collect the
variables on the left, since 11 > 7.		 11p − 36 − 7p > 7p − 28 − 7p
Simplify. 4p − 36 > −28
Add 36 to both sides to collect the
constants on the right.		 4p − 36 + 36 > −28 + 36
Simplify. 4p > 8
Divide both sides of the inequality by
4; the inequality stays the same.		 \displaystyle\frac{4p}{4}>\frac{8}{4}
Simplify. p > 2
Graph the solution on the number line. Graph the solution on the number line with a left paarenthesis at 2 with shading to the right.

 
Write the solution in interval notation. (2, ∞)

Unusual Solution Sets

Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.

Try it!

Solve the inequality 8x − 2(5 − x) < 4(x + 9) + 6x, graph the solution on the number line, and write the solution in interval notation.

Solution

Steps Algebraic
Simplify each side as much as possible. 8x − 2(5 − x) < 4(x + 9) + 6x
Distribute. 8x − 10 + 2x < 4x + 36 + 6x
Combine like terms. 10x − 10 < 10x + 36
Subtract 10x from both sides to collect
the variables on the left.		 10x − 10 − 10x < 10x + 36 − 10x
Simplify. −10 < 36
The x’s are gone, and we have a true
statement.		 The inequality is an identity.
The solution is all real numbers.
Graph the solution on the number line.
Graph the solution all real numbers on the number line. The number line is shaded for all values. Write the solution in interval notation. It is negative infinity to infinity within parentheses.
Write the solution in interval notation. (−∞, ∞)

Fractions and Inequalities

We can clear fractions in inequalities much as we did in equations. Again, be careful with the signs when multiplying or dividing by a negative.

Try it!

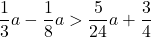  1. Solve the inequality \displaystyle\frac{1}{3}a-\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}, graph the solution on the number line, and write the solution in interval notation.

Solution

Steps Algebraic
Inequality
One-third a minus one-eighth a is greater than five twenty-fourths a plus three-fourths.
Multiply both sides by the LCD, 24,
to clear the fractions.
Multiply both sides by the L C D, 24, to clear the fractions. 24 times the quantity One-third a minus one-eighth a is greater than 24 times the quantity five twenty-fourths a plus three-fourth.
Simplify.
Simplify. 8 a minus 3 a is greater than 5 a plus 18.
Combine like terms.
Combine like terms. 5a is greater than 5a plus 18
Subtract 5a from both sides to collect the
variables on the left.
Subtract 5 a from both sides to collect the variables on the left. 5 a minus 5 a is greater than 5 a minus 5 a plus 18.
Simplify.
Simplify. 0 is less than 18.
The statement is false. The inequality is a contradiction.
There is no solution.
Graph the solution on the number line.
The statement is false. The inequality is a contradiction. There is no solution. As a result, there is no graph on the number line or interval notation.
Write the solution in interval notation. There is no solution.

2. Solve the inequality \displaystyle\frac{1}{4}x-\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8},  graph the solution on the number line, and write the solution in interval notation.

Solution


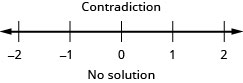
he inequality is a contradiction. So, there is no solution. As a result, there is no graph on the number line or interval notation.

3. Solve the inequality \displaystyle\frac{2}{5}z-\frac{1}{3}z<\frac{1}{15}z-\frac{3}{5}, graph the solution on the number line, and write the solution in interval notation.

Solution


The inequality is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.

Compound Inequalities

Now that we know how to solve linear inequalities, the next step is to look at compound inequalities. A compound inequality is made up of two inequalities connected by the word “and” or the word “or.” For example, the following are compound inequalities.

x + 3 > −4 and 4x − 5 ≤ 3
2(y + 1) < 0 or y − 5 ≥ −2

Compound Inequality

A compound inequality is made up of two inequalities connected by the word “and” or the word “or.”

For now, we are going to only focus on the “and” form of compound inequalities. There are two ways to solve compound inequalities: separating them into two separate inequalities or leaving the compound inequality intact and performing operations on all three parts at the same time. We will illustrate both methods.

Method 1 – Separate inequalities

To solve a compound inequality means to find all values of the variable that make the compound inequality a true statement. We solve compound inequalities using the same techniques we used to solve linear inequalities. We solve each inequality separately and then consider the two solutions.

To solve a compound inequality with the word “and,” we look for all numbers that make both inequalities true.

Let’s start with the compound inequalities with “and.” Our solution will be the numbers that are solutions to both inequalities known as the intersection of the two inequalities. Consider the intersection of two streets—the part where the streets overlap—belongs to both streets.


The figure is an illustration of two streets with their intersection shadedTo find the solution of the compound inequality, we look at the graphs of each inequality and then find the numbers that belong to both graphs—where the graphs overlap.

For the compound inequality x > −3 and x ≤ 2, we graph each inequality. We then look for where the graphs “overlap”. The numbers that are shaded on both graphs, will be shaded on the graph of the solution of the compound inequality.


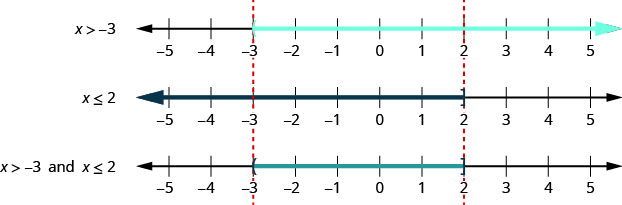
The figure shows the graph of x is greater than negative 3 with a left parenthesis at negative 3 and shading to its right, the graph of x is less than or equal to 2 with a bracket at 2 and shading to its left, and the graph of x is greater than negative 3 and x is less than or equal to 2 with a left parenthesis at negative 3 and a right parenthesis at 2 and shading between negative 3 and 2. Negative 3 and 2 are marked by lines on each number line.

We can see that the numbers between −3 and 2 are shaded on both of the first two graphs. They will then be shaded on the solution graph.

The number −3 is not shaded on the first graph and so since it is not shaded on both graphs, it is not included on the solution graph.

The number two is shaded on both the first and second graphs. Therefore, it is be shaded on the solution graph.

This is how we will show our solution in the next examples.

Try it!

Solve 6x − 3 < 9 and 2x + 9 ≥ 3. Graph the solution and write the solution in interval notation.

Solution

Steps Algebraic
1. Solve each
inequality.		 6x − 3 < 9 and 2x + 9 ≥ 3
Simplify 6x < 12 and 2x ≥ −6
Solution x < 2 and x ≥ −3
2. Graph each solution. Then graph the numbers that make both inequalities true. The final graph will show all the numbers that make both inequalities true—the numbers shaded on both of the first two graphs. 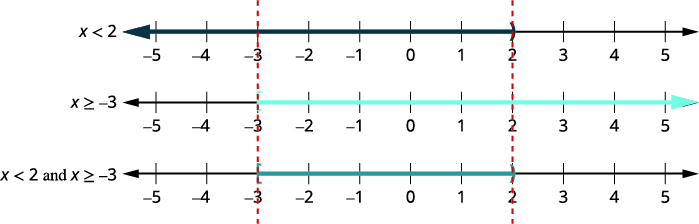The graph of x is less than 2 has a right parenthesis at 2 and is shaded to its left. The graph of x is greater than or equal to negative 3 has a left bracket at negative 3 and is shaded to its right. Then graph the numbers that make both inequalities true. The final graph will show all the numbers that make both inequalities true—the numbers shaded on both of the first two graphs. The graph of x is less than 2 and x is greater than or equal to negative 3 has a left bracket at negative 3 and a right parenthesis at 2 and is shaded between the bracket and parenthesis. Each graph is marked at negative 3 and 2.
3. Write the solution in interval notation. [−3, 2)
All the numbers that make both inequalities true are the solution to the compound inequality.
How to solve a compound inequality with “and.”
  1. Solve each inequality.
  2. Graph each solution. Then graph the numbers that make both inequalities true.
    This graph shows the solution to the compound inequality.
  3. Write the solution in interval notation.

Try it!

  1. Solve 3(2x + 5) ≤ 18 and 2(x − 7)< −6. Graph the solution and write the solution in interval notation.

Solution

Steps Algebraic
Solve each
inequality.		 6x + 15 ≤ 18 and 2x − 14 < −6
Simplify 6x ≤ 3 and 2x < 8
Solution \displaystyle x\leq\frac{1}{2} and x < 4
Graph each
solution.		 The graph of x is less than or equal to one-half has a right bracket at one-half and is shaded to the left. The graph of x is less than 4 has a right parenthesis and is shaded to the left. Both graphs are marked at one-half. Graph the numbers that make both inequalities true. Graph the numbers that make both inequalities true. The graph has a right bracket at one-half and is shaded to the left. It is marked at one-half.
Graph the numbers
that make both
inequalities true.		 The graph has a right bracket at one-half and is shaded to the left. It is marked at one-half.
Write the solution
in interval notation.		 \displaystyle\left(-\infty,\frac{1}{2}\right]

2. Solve \displaystyle\frac{1}{3}x-4\geq -2 and −2(x − 3) ≥ 4. Graph the solution and write the solution in interval notation.

Solution

Steps Algebraic
Inequality \displaystyle\frac{1}{3}x-4\geq -2 and −2(x − 3) ≥ 4
Solve each
inequality.		 \displaystyle\frac{1}{3}x-4\geq -2 and −2x + 6 ≥ 4
Simplify \displaystyle\frac{1}{3}x\geq 2 and −2x ≥ −2
Solution x ≥ 6 and x ≤ 1
Graph each solution. The graph of x is greater than or equal to 6 has a left bracket at 6 and is shaded to its right. The graph of x is less than or equal to 1 has a right bracket at 1 and is shaded to its left.
Graph the numbers that
make both inequalities
true.		 Graph the numbers that make both inequalities true. Notice that there are no numbers that make the inequalities true.
There are no numbers that make both inequalities true.

This is a contradiction so there is no solution.
Method 2 – Operate on all 3 parts
Sometimes we have a compound inequality that can be written more concisely. For example, a < x and x < b can be written simply as a < x < b and then we call it a double inequality. The two forms are equivalent.
Double Inequality

A double inequality is a compound inequality such as a < x < b. It is equivalent to a < x and x < b.

Other forms: a < x < b is equivalent to a < x and x < b
 a ≤ x ≤ b is equivalent to a ≤ x and x ≤ b
a > x > b is equivalent to a > x and x > b
a ≥ x ≥ b is equivalent to a ≥ x and x ≥ b

To solve a double inequality, we perform the same operation on all three “parts” of the double inequality with the goal of isolating the variable in the center.

Try it!

Solve −4 ≤ 3x − 7 < 8. Graph the solution and write the solution in interval notation.

Solution

Steps Algebraic
Inequality Negative 4 is less than or equal to 3 x minus 7 which is less than 8.
Add 7 to all three parts. Add 7 to all three parts. Negative 4 plus 7 is less than or equal to 3 x minus 7 plus 7 which is less than 8 plus 7.
Simplify. Simplify. 3 is less than or equal to 3 x which is less than 15.
Divide each part by three. Divided each part by 3. 3 divided by 3 is less than or equal to 3 x divided by 3 which is less than 15 divided by 3.
Simplify. Simplify. The result is 1 is less than or equal to x which is less than 5.
Graph the solution. Graph the solution. The solution on a number line is a left bracket at 1, a right parenthesis at 5, and shading between the bracket and parenthesis.
Write the solution in interval notation. Write the solution in interval notation. It is 1 to 5 within a bracket and a parenthesis.

When written as a double inequality, 1 ≤ x < 5, it is easy to see that the solutions are the numbers caught between one and five, including one, but not five. We can then graph the solution immediately as we did above.

Another way to graph the solution of 1 ≤ x < 5 is to graph both the solution of  x ≥ 1 and the solution of x < 5. We would then find the numbers that make both inequalities true as we did in previous examples.

Try it!

  1. Solve the compound inequality. Graph the solution and write the solution in interval notation: −5 ≤ 4x − 1 < 7.

Solution


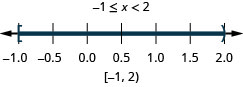
The solution is negative 1 is less than or equal to x which is less than 2. Its graph has a closed circle at negative 1 and an open circle at 2 with shading between the closed and open circles. Its interval notation is negative 1 to 2 within a bracket and a parenthesis.

2. Solve the compound inequality. Graph the solution and write the solution in interval notation: −3 < 2x − 5 ≤ 1.

Solution


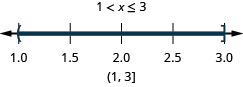
The solution is 1 is less than x which is less than or equal to 3. Its graph has an open circle at 1 and a closed circle at 3 with shading between the closed and open circles. Its interval notation is negative 1 to 3 within a parenthesis and a bracket.

The next example demonstrates solving the inequality using both methods described above.

Try it!

Solve the compound inequality: 3 ≤ 2x + 2 < 6. 

Solution

Steps

The first method is to write two separate inequalities: 3 ≤ 2x + 2 and 2x + 2 < 6.

We solve them independently.

3 ≤ 2x + 2      and      2x + 2 < 6
1 ≤ 2x                        2x < 4
\displaystyle\frac{1}{2}\leq x                     x < 2

Then, we can rewrite the solution as a compound inequality, the same way the problem began.

\displaystyle\frac{1}{2}\leq x<2

In interval notation, the solution is written as \displaystyle\left[\frac{1}{2}, 2\right).

The second method is to leave the compound inequality intact, and perform solving procedures on the three parts at the same time.

3  ≤  2x + 2 < 6
1 ≤ 2x < 4    Isolate the variable term, and subtract 2 from all three parts.
\displaystyle\frac{1}{2}\leq x<2  Divide through all three parts by 2.

We get the same solution: \displaystyle\left[\frac{1}{2}, 2\right).

Access this online resource for additional instruction and practice with linear inequalities and solving compound inequalities.

Solve Applications with Linear Inequalities

Many real-life situations require us to solve inequalities. The method we will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations.

We will read the problem and make sure all the words are understood. Next, we will identify what we are looking for and assign a variable to represent it. We will restate the problem in one sentence to make it easy to translate into an inequality. Then, we will solve the inequality.

Sometimes an application requires the solution to be a whole number, but the algebraic solution to the inequality is not a whole number. In that case, we must round the algebraic solution to a whole number. The context of the application will determine whether we round up or down.

Try it!

  1. Dawn won a mini-grant of $4,000 to buy tablet computers for her classroom. The tablets she would like to buy cost $254.12 each, including tax and delivery. What is the maximum number of tablets Dawn can buy?

Solution

Steps Algebraic
1. Read the problem. NA
2. Identify what you are looking for. the maximum number of tablets Dawn can buy
3. Name what you are looking for.
Choose a variable to represent that quantity. Let n = the number of tablets.
4. Translate. Write a sentence that gives the information to find it. $254.12 times the number of tablets is no more than $4,000.
Translate into an inequality. 254.12n ≤ 4000
5. Solve the inequality. n ≤ 15.74
But n must be a whole number of tablets, so round to 15. n ≤ 15
6. Check the answer in the problem and make sure it makes sense. Rounding down the price to $250, 15 tablets would cost $3,750, while 16 tablets would be $4,000. So a maximum of 15 tablets at $254.12 seems reasonable.
7. Answer the question with a complete sentence. Dawn can buy a maximum of 15 tablets.

2. Taleisha’s phone plan costs her $28.80 a month plus $0.20 per text message. How many text messages can she send/receive and keep her monthly phone bill no more than $50?

Solution

Steps Algebraic
1. Read the problem. NA
2. Identify what you are looking for. the number of text messages Taleisha can make
3. Name what you are looking for.  Let t = the number of text messages.
Choose a variable to represent that quantity.
4. Translate. Write a sentence that gives the information to find it.  $28.80 plus $0.20 times the number of text messages is less than or equal to $50.
Translate into an inequality. 28.80 + 0.20t ≤ 50
5. Solve the inequality.  0.2t ≤ 21.2
t ≤ 106 text messages
6. Check the answer in the problem and make sure it makes sense.  Yes, 28.80 + 0.20(106) = 50.
7. Answer the question with a complete sentence. Taleisha can send/receive no more than 106 text messages to keep her bill no more than $50.

Profit is the money that remains when the costs have been subtracted from the revenue. In the next example, we will find the number of jobs a small businesswoman needs to do every month in order to make a certain amount of profit.

Try it!

Felicity has a calligraphy business. She charges $2.50 per wedding invitation. Her monthly expenses are $650. How many invitations must she write to earn a profit of at least $2,800 per month?

Solution

Steps Algebraic
1. Read the problem. NA
2. Identify what you are looking for. the number of invitations Felicity needs to write
3. Name what you are looking for. Let j = the number of invitations.
Choose a variable to represent that quantity.
4. Translate. Write a sentence that gives the information to find it. $2.50 times the number of invitations minus $650 is at least $2,800.
Translate into an inequality. 2.50j − 650 ≥ 2,800
5. Solve the inequality. 2.5j ≥ 3,450
  j ≥ 1,380 invitations
6. Check the answer in the problem and make sure it makes sense. If Felicity wrote 1400 invitations, her profit would be 2.50(1400) − 650, or $2,850. This is more than $2800.
7. Answer the question with a complete sentence. Felicity must write at least 1,380 invitations.

There are many situations in which several quantities contribute to the total expense. We must make sure to account for all the individual expenses when we solve problems like this.

Try it!

Malik is planning a six-day summer vacation trip. He has $840 in savings, and he earns $45 per hour for tutoring. The trip will cost him $525 for airfare, $780 for food and sightseeing, and $95 per night for the hotel. How many hours must he tutor to have enough money to pay for the trip?

Solution

Steps Algebraic
1. Read the problem. NA
2. Identify what you are looking for. the number of hours Malik must tutor
3. Name what you are looking for. Let h = the number of hours
Choose a variable to represent that quantity.
4. Translate. Write a sentence that gives the information to find it. The expenses must be less than or equal to the income. The cost of airfare plus the cost of food and sightseeing and the hotel bill must be less than the savings plus the amount earned tutoring.
Translate into an inequality. 525 + 780 + 95(6) ≤ 840 + 45h
5. Solve the inequality.



 1,875 ≤ 840 + 45h
1,035 ≤ 45h
23 ≤ h
h ≥ 23
6. Check the answer in the problem and make sure it makes sense.



 We substitute 23 into the inequality.
1,875 ≤ 840 + 45h
1,875 ≤ 840 + 45(23)
1,875 ≤ 1875
7. Answer the question with a complete sentence. Malik must tutor at least 23 hours.

Key Concepts

  • Inequalities, Number Lines, and Interval Notation
    The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.
  • Linear Inequality
    • A linear inequality is an inequality in one variable that can be written in one of the following forms where a, b, and c are real numbers and a ≠ 0:
      ax + b < c,     ax + b ≤ c,      ax + b > c,      ax + b ≥ c.
  • Addition and Subtraction Property of Inequality
    • For any numbers a, b, and c, if a < b, then 
      a + c < b + c           a − c < b − c

      a + c > b + c           a − c > b − c 

    • We can add or subtract the same quantity from both sides of an inequality and still keep the inequality.
  • Multiplication and Division Property of Inequality
    • For any numbers a, b, and c,
      multiply or divide by a positive

if a < b and c > 0, then ac < bc and \displaystyle\frac{a}{c}<\frac{b}{c}.

if a > b and c > 0, then ac > bc and \displaystyle\frac{a}{c}>\frac{b}{c}.

    • multiply or divide by a negative

if a < b and c < 0, then ac > bc and \displaystyle\frac{a}{c}>\frac{b}{c}.

if a > b and c < 0, then ac < bc and \displaystyle\frac{a}{c}<\frac{b}{c}.

  • Phrases that indicate inequalities

    > ≥ < ≤
    is greater than

    is more than

    is larger than

    exceeds    		 is greater than or equal to

    is at least

    is no less than

    is the minimum    		 is less than

    is smaller than

    has fewer than

    is lower than    		 is less than or equal to

    is at most

    is no more than

    is the maximum
  • Absolute Value
    The absolute value of a number is its distance from 0 on the number line.
    The absolute value of a number n is written as |n| and |n| ≥ 0 for all numbers.
    Absolute values are always greater than or equal to zero.
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0572 Corequisite Support Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book