"

19 Logarithmic Functions

Topics Covered:[1]

Function and Inverse Reminders

  • Horizontal Line Test: If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function.
  • Inverse of a Function Defined by Ordered Pairs: If f(x) is a one-to-one function whose ordered pairs are of the form (x, y), then its inverse function f-1(x) is the set of ordered pairs (y, x).
  • Inverse Functions: For every x in the domain of one-to-one function f and f-1,

f-1(f(x)) = x

f(f-1(x)) = x

  • How to Find the Inverse of a One-to-One Function:
        1. Substitute y for f(x).
        2. Interchange the variables x and y.
        3. Solve for y.
        4. Substitute f-1(x) for y.
  • The inverse function ‘undoes’ what the original function did to a value in its domain in order to get back to the original x-value. This holds for all x in the domain of f. Informally, this means that inverse functions “undo” each other. However, only one-to-one functions have inverses that are functions.

We have spent some time finding the inverse of many functions. It works well to ‘undo’ an operation with another operation. Subtracting ‘undoes’ addition, multiplication ‘undoes’ division, taking the square root ‘undoes’ squaring.

As we studied the exponential function, we saw that it is one-to-one as its graphs pass the horizontal line test. This means an exponential function does have an inverse. If we try our algebraic method for finding an inverse, we run into a problem.

Steps Algebraic
Function f(x) = ax
Rewrite with y = f(x). y = ax
Interchange the variables x and y. x = ay
Solve for y. Oops! We have no way to solve for y!

To deal with this we define the logarithm function with base a to be the inverse of the exponential function f(x) = ax.

We use the notation f−1(x) = logax and say the inverse function of the exponential function is the logarithmic function.

Logarithmic Function

The function f(x) = logax is the logarithmic function with base a, where a > 0, x > 0, and a ≠ 1.

y = logax is equivalent to x = ay

Convert Between Exponential and Logarithmic Forms

Since the equations y = logax  and x = ay are equivalent, we can go back and forth between them. This will often be the method to solve some exponential and logarithmic equations. To help with converting back and forth let’s take a close look at the equations. See the figure below. Notice the positions of the exponent and base.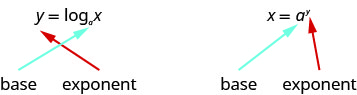This figure shows the expression y equals log sub a of x, where y is the exponent and a is the base. Next to this expression we have x equals a to the y, where again y is the exponent and a is the base.If we realize the logarithm is the exponent it makes the conversion easier. You may want to repeat, “base to the exponent give us the number.”

Can we take the logarithm of a negative number?

No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.

Try it!

Convert to logarithmic form:

a. 23 = 8

b. \displaystyle 5^{\frac{1}{2}}=\sqrt{5}

c. \displaystyle\left(\frac{1}{2}\right)^{x}=\frac{1}{16}.

Solution (click to reveal)

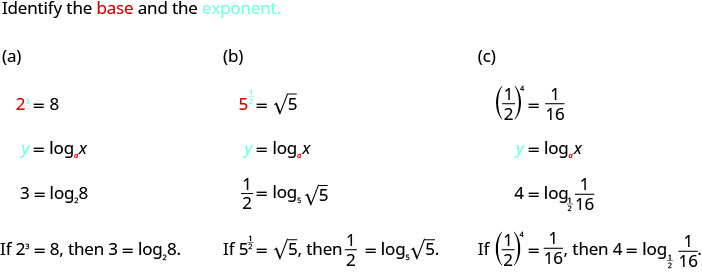
In part (a) we have 2 to the 3 power equals 8, where the 2 is red and the 3 is blue. Following this, we have blue y equals log sub red a of x. Then 3 equals log sub 2 of 8. Hence, if 2 cubed equals 8, then 3 equals log sub 2 of 8. In part (b) we have 5 to the 1 over 2 power equals square root of 5, where the 5 is red and the 1 over 2 is blue. Following this, we have blue y equals log sub red a of x. Then 1 over 2 equals log sub 5 of the square root of 5. Hence, if 5 to the 1 over 2 power equals the square root of 5, then 1 over 2 equals log sub 5 of the square root of 5. In part (c) we have 1 over 2 to the x power equals 1 over 16, where the 1 over 2 is red and the x is blue. Following this, we have blue y equals log sub red a of x. Then x equals log sub 1 over 2 of 1 over 16. Hence, if 1 over 2 to the x power equals 1 over 16, then x equals log sub 1 over 2 of 1 over 16.

 

Convert to logarithmic form:

a. 32 = 9

b. \displaystyle 7^{\frac{1}{2}}=\sqrt{7} 

c. \displaystyle\left(\frac{1}{3}\right)^{x}=\frac{1}{27}

Solution (click to reveal)

a.  log39 = 2

b. \displaystyle log_{7}\sqrt{7}=\frac{1}{2}

c. \displaystyle log_{\frac{1}{3}}\frac{1}{27}=x

 

Convert to logarithmic form:

a. 43 = 64

b. \displaystyle 4^{\frac{1}{3}}=\sqrt[3]{4}

c. \displaystyle\left(\frac{1}{2}\right)^{x}=\frac{1}{32}

Solution (click to reveal)

a. log464 = 3

b. \displaystyle log_{4}\sqrt[3]{4}=\frac{1}{3}

c. \displaystyle log_{\frac{1}{2}}\frac{1}{32}=x

 

In the next example we do the reverse—convert logarithmic form to exponential form.

Try it!

Convert to exponential form:

a. 2 = log864

b. 0 = log41

c. \displaystyle -3=log_{10}\frac{1}{1000}.

Solution (click to reveal)


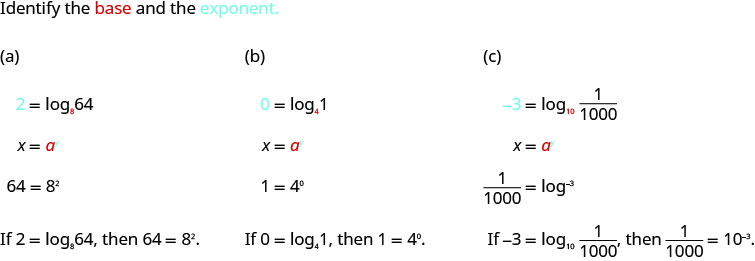
In part (a) we have 2 equals log sub 8 of 64, where the 2 is blue and the 8 is red. Following this, we have x equals red a to the blue y power. Then 64 equals 8 squared. Hence, if 2 equals log sub 8 of 64, then 64 equals 8 squared. In part (b) we have 0 equals log sub 4 of 1, where the 0 is blue and the 4 is red. Following this, we have x equals red a to the blue y power. Then 1 equals 4 to the zero power. Hence, if 0 equals log sub 4 of 1, then 1 equals 4 to the zero power. In part (c) we have negative 3 equals log sub 10 of 1 over 1000, where the negative 3 is blue and the 10 is red. Following this, we have x equals red a to the blue y power. Then 1 over 1000 equals 10 to the negative three power. Hence, if negative 3 equals log sub 10 of 1 over 1000, then 1 over 1000 equals 10 to the negative 3 power.

 

Convert to exponential form:

a. 3 = log464

b. 0 = logx1

c. \displaystyle -2=log_{10}\frac{1}{100}

Solution (click to reveal)

 

a. 64 = 43

b. 1 = x0

c. \displaystyle\frac{1}{100}=10^{-2}

 

Evaluate Logarithmic Functions

We can solve and evaluate logarithmic equations by using the technique of converting the equation to its equivalent exponential equation.

Try it!

Find the value of x:

a. logx36 = 2

b. log4x = 3

c. \displaystyle log_{\frac{1}{2}}\frac{1}{8}=x.

Solution A (click to reveal)

a.

Steps Algebraic
Logarithm logx36 = 2
Convert to exponential form. x2 = 36
Solve the quadratic. x = 6 or x = −6
The base of a logarithmic function must be
positive, so we eliminate x = −6.		 x = 6 
Therefore, log636 = 2.

 

Solution B (click to reveal)

b.

Steps Algebraic
Logarithm log4x = 3
Convert to exponential form. 43 = x
Simplify. x = 64
Therefore, log464 = 3.

 

Solution C (click to reveal)

c.

Steps Algebraic
Logarithm \displaystyle log_{\frac{1}{2}}\frac{1}{8}=x
Convert to exponential form. \displaystyle\left(\frac{1}{2}\right)^{x}=\frac{1}{8}
Rewrite \displaystyle\frac{1}{8} as \displaystyle\left(\frac{1}{2}\right)^{3}. \displaystyle\left(\frac{1}{2}\right)^{x}=\left(\frac{1}{2}\right)^{3}
With the same base, the exponents must be equal. x = 3
Therefore, \displaystyle log_{\frac{1}{2}}\frac{1}{8}=3.

 

Find the value of x:

a. logx64 = 2

b. log5x = 3

c. \displaystyle log_{\frac{1}{2}}\frac{1}{4}=x

Solution (click to reveal)

a. x = 8

b. x = 125

c. x = 2

 

When see an expression such as log327, we can find its exact value in two ways. By inspection we realize it means “3 to what power will be 27?” Since 33 = 27, we know log327 = 3. An alternate way is to set the expression equal to x and then convert it into an exponential equation.

Now consider solving log749 and log327 mentally.

  • We ask, “To what exponent must 7 be raised in order to get 49?” We know 72 = 49. Therefore, log749 = 2
  • We ask, “To what exponent must 3 be raised in order to get 27?” We know 33 = 27. Therefore, log327 = 3

Even some seemingly more complicated logarithms can be evaluated without a calculator. For example, let’s evaluate \displaystyle log_{\frac{2}{3}}\frac{4}{9} mentally.

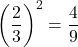  • We ask, “To what exponent must \displaystyle\frac{2}{3} be raised in order to get \displaystyle\frac{4}{9}?” We know 22 = 4 and 32 = 9, so \displaystyle\left(\frac{2}{3}\right)^{2}=\frac{4}{9}. Therefore, \displaystyle log_{\frac{2}{3}}\left(\frac{4}{9}\right)=2.

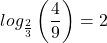Try it!

Find the exact value of each logarithm without using a calculator:

a. log525

b. log93

c. \displaystyle log_{2}\frac{1}{16}.

Solution A (click to reveal)

a.

Steps Algebraic
Logarithm log525
5 to what power will be 25? log525 = 2
Or
Set the expression equal to x. log525 = x
Change to exponential form. 5x = 25
Rewrite 25 as 52. 5x = 52
With the same base the exponents must be equal. x = 2
Therefore, log525 = 2.

 

Solution B (click to reveal)

b.

Steps Algebraic
Logarithm log93
Set the expression equal to x. log93 = x
Change to exponential form. 9x = 3
Rewrite 9 as 32. (32)x = 31
Simplify the exponents. 32x = 31
With the same base the exponents must be equal. 2x = 1
Solve the equation. \displaystyle x=\frac{1}{2}
Therefore, \displaystyle log_{9}3=\frac{1}{2}.

 

Solution C (click to reveal)

c.

Steps Algebraic
Logarithm \displaystyle log_{2}\frac{1}{16}
Set the expression equal to x. \displaystyle log_{2}\frac{1}{16}=x
Change to exponential form. \displaystyle 2^{x}=\frac{1}{16}
Rewrite 16 as 24. \displaystyle 2^{x}=\frac{1}{2^{4}}
2x = 2-4
With the same base the exponents must be equal. x = −4
Therefore, \displaystyle log_{2}\frac{1}{16}=-4.

 

 Find the exact value of each logarithm without using a calculator:

a. log12144
b. log42
c. \displaystyle log_{2}\frac{1}{32}

Solution (click to reveal)

a. 2

b. \displaystyle\frac{1}{2}

c. −5

 

Basic Log Properties

Now that we have learned about exponential and logarithmic functions, we can introduce some of the properties of logarithms. These will be very helpful as we continue to solve both exponential and logarithmic equations.

The first two properties derive from the definition of logarithms. Since a0 = 1, we can convert this to logarithmic form and get loga1 = 0. Also, since a1 = a, we get logaa = 1.

Properties of Logarithms
loga1 = 0          logaa = 1

In the next example we could evaluate the logarithm by converting to exponential form, as we have done previously, but recognizing and then applying the properties saves time.

Try it!

Evaluate using the properties of logarithms:

a. log81

b. log66.

Solution A (click to reveal)

a.

Steps Algebraic
Logarithm log81
Use the property, loga1 = 0. log81 = 0

 

Solution B (click to reveal)

b.

Steps Algebraic
Logarithm log66
Use the property, logaa = 1. log66 = 1

 

 Evaluate using the properties of logarithms:

a. log131

b. log99.

Solution (click to reveal)

a. 0

b. 1

 

The next two properties can also be verified by converting them from exponential form to logarithmic form, or the reverse.

The exponential equation alogax = x converts to the logarithmic equation logax = logax, which is a true statement for positive values for x only.

The logarithmic equation logaax = x converts to the exponential equation ax = ax, which is also a true statement.

These two properties are called inverse properties because, when we have the same base, raising to a power “undoes” the log and taking the log “undoes” raising to a power. These two properties show the composition of functions. Both ended up with the identity function which shows again that the exponential and logarithmic functions are inverse functions.

Inverse Properties of Logarithms

For a > 0, x > 0 and a ≠ 1,

alogax = x  and logaax = x

In the next example, apply the inverse properties of logarithms.

Try it!

Evaluate using the properties of logarithms:

a. 4log49

b. log335.

Solution A (click to reveal)

a.

Steps Algebraic
Logarithm 4log49
Use the property, alogax = x. 4log49 = 9

 

Solution B (click to reveal)

b.

Steps Algebraic
Logarithm log335
Use the property, alogax = x. log335 = 5

 

 Evaluate using the properties of logarithms:

a. 5log515

b. log774

Solution (click to reveal)

a. 15

b. 4

 

Graphing Logarithmic Functions

To graph a logarithmic function y = logax, it is easiest to convert the equation to its exponential form, x = ay.

Generally, when we look for ordered pairs for the graph of a function, we usually choose an x-value and then determine its corresponding y-value. In this case you may find it easier to choose y-values and then determine its corresponding x-value.

We begin with the parent function y = loga(x). Because every logarithmic function of this form is the inverse of an exponential function with the form y = ax, their graphs will be reflections of each other across the line y = x. To illustrate this, we can observe the relationship between the input and output values of y = 2x and its equivalent x = log2(y) in the table below.

Input values x = −3 x =−2 x =−1 x = 0 x = 1 x = 2 x = 3
2x = y \displaystyle\frac{1}{8} \displaystyle\frac{1}{4} \displaystyle\frac{1}{2} 1 2 4 8
log2(y) = x −3 −2 −1 0 1 2 3

Using the inputs and outputs from the table, we can build another table to observe the relationship between points on the graphs of the inverse functions f(x) = 2x and g(x) = log2(x). See the table below.

Functions x = −3 x =−2 x =−1 x = 0 x = 1 x = 2 x = 3
f(x) = 2x \displaystyle\left(-3,\frac{1}{8}\right) \displaystyle\left(-2,\frac{1}{4}\right) \displaystyle\left(-1,\frac{1}{2}\right) \displaystyle(0,1) \displaystyle(1,2) \displaystyle(2,4) \displaystyle(3,8)
g(x) = log2(x) \displaystyle\left(\frac{1}{8}, -3\right) \displaystyle\left(\frac{1}{4}, -2\right) \displaystyle\left(\frac{1}{2}, -1\right) \displaystyle(1,0) \displaystyle(2,1) \displaystyle(4,2) \displaystyle(8,3)

As we’d expect, the x– and y-coordinates are reversed for the inverse functions. The figure below shows the graph of f and g.

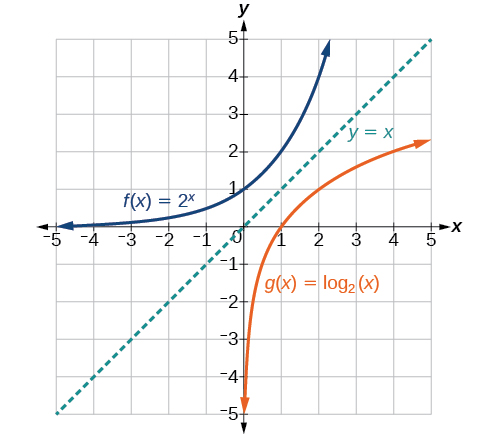
Graph of two functions, f(x)=2^x and g(x)=log_2(x), with the line y=x denoting the axis of symmetry.
Notice that the graphs of f(x) = 2x and g(x) = log2(x) are reflections about the line y = x.

Try it!

Graph y = log2x.

Solution (click to reveal)

To graph the function, we will first rewrite the logarithmic equation, y = log2x, in exponential form, 2y = x.

We will use point plotting to graph the function. It will be easier to start with values of y and then get x.

y 2y = x (x, y)
−2 \displaystyle 2^{-2}=\frac{1}{2^{2}}=\frac{1}{4} \displaystyle\left(\frac{1}{4},2\right)
−1 \displaystyle 2^{-1}=\frac{1}{2^{1}}=\frac{1}{2} \displaystyle\left(\frac{1}{2},-1\right)
0 20 = 1 (1, 0)
1 21 = 2 (2, 1)
2 22 = 4 (4, 2)
3 23 = 8 (8, 3)

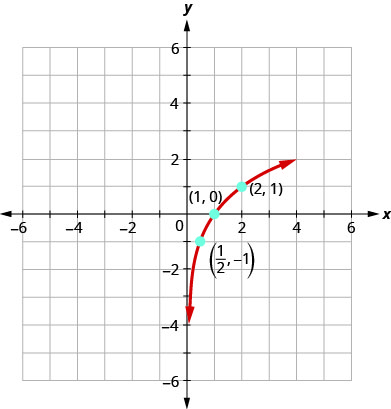
This figure shows the logarithmic curve going through the points (1 over 2, negative 1), (1, 0), and (2, 1).

 

Graph: y = log3x.

Solution (click to reveal)

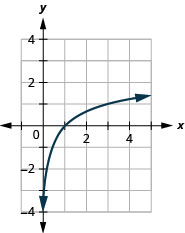
This figure shows the logarithmic curve going through the points (1 over 3, negative 1), (1, 0), and (3, 1).

 

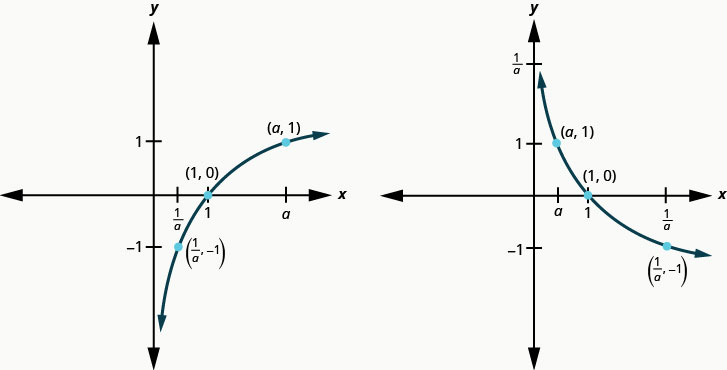
The graphs of y = log2x, and y = log3x, are the shape we expect from a logarithmic function where a > 1.

We notice that for each function the graph contains the point (1, 0). This make sense because 0 = loga1 means a0 = 1 which is true for any a.

The graph of each function, also contains the point (a, 1). This makes sense as 1 = logaa means a1 = a. which is true for any a.

Notice too, the graph of each function y = logax also contains the point \displaystyle\left(\frac{1}{a},-1\right). This makes sense as \displaystyle -1=log_{a}\frac{1}{a} means \displaystyle a^{-1}=\frac{1}{a}, which is true for any a.

Look at each graph again. Now we will see that many characteristics of the logarithm function are simply ’mirror images’ of the characteristics of the corresponding exponential function.

What is the domain of the function? The graph never hits the y-axis. The domain is all positive numbers. We write the domain in interval notation as (0, ∞).

What is the range for each function? From the graphs we can see that the range is the set of all real numbers. There is no restriction on the range. We write the range in interval notation as (−∞, ∞).

When the graph approaches the y-axis so very closely but will never cross it, we call the line x = 0, the y-axis, a vertical asymptote.

Properties of the Graph of y = logax when a > 1

Property Answer
Domain (0, ∞)
Range (−∞, ∞)
x-intercept (1, 0)
y-intercept None
Contains (a, 1), \displaystyle\left(\frac{1}{a},-1\right)
Asymptote y-axis

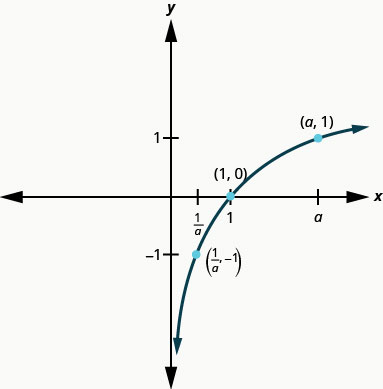
This figure shows the logarithmic curve going through the points (1 over a, negative 1), (1, 0), and (a, 1).

Our next example looks at the graph of y = logax when 0 < a < 1.

Try it!

Graph \displaystyle y=log_{\frac{1}{3}}x.

Solution (click to reveal)

 

To graph the function, we will first rewrite the logarithmic equation, \displaystyle y=log_{\frac{1}{3}}x in exponential form, \displaystyle\left(\frac{1}{3}\right)^{y}=x.

We will use point plotting to graph the function. It will be easier to start with values of y and then get x.

y \displaystyle\left(\frac{1}{3}\right)^{y}=x (x, y)
−2 \displaystyle\left(\frac{1}{3}\right)^{-2}=3^{2}=9 (9, −2)
−1 \displaystyle\left(\frac{1}{3}\right)^{-1}=3^{1}=3 (3, −1)
0 \displaystyle\left(\frac{1}{3}\right)^{0}=1 (1, 0)
1 \displaystyle\left(\frac{1}{3}\right)^{1}=\frac{1}{3} \displaystyle\left(\frac{1}{3},1\right)
2 \displaystyle\left(\frac{1}{3}\right)^{2}=\frac{1}{9} \displaystyle\left(\frac{1}{9},2\right)
3 \displaystyle\left(\frac{1}{3}\right)^{3}=\frac{1}{27} \displaystyle\left(\frac{1}{27},3\right)

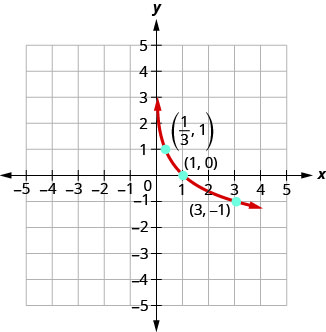
This figure shows the logarithmic curve going through the points (1 over 3, 1), (1, 0), and (3, negative 1).

 

The graphs of all have the same basic shape. While this is the shape we expect from a logarithmic function where 0 < a < 1.

We notice, that for each function again, the graph contains the points, (1, 0), (a, 1), \displaystyle\left(\frac{1}{a},-1\right). This make sense for the same reasons we argued above.

We notice the domain and range are also the same—the domain is (0, ∞) and the range is (−∞, ∞). The y-axis is again the vertical asymptote.

Properties of the Graph of y = logax

when a > 1 when 0 < a < 1
Domain (0, ∞) Domain (0, ∞)
Range (−∞, ∞) Range (−∞, ∞)
x-intercept (1, 0) x-intercept (1, 0)
y-intercept none y-intercept None
Contains (a, 1), \displaystyle\left(\frac{1}{a}.-1\right) Contains (a, 1), \displaystyle\left(\frac{1}{a}.-1\right)
Asymptote y-axis Asymptote y-axis
Basic shape increasing Basic shape Decreasing

This figure shows that, for a greater than 1, the logarithmic curve going through the points (1 over a, negative 1), (1, 0), and (a, 1). This figure shows that, for a greater than 0 and less than 1, the logarithmic curve going through the points (a, 1), (1, 0), and (1 over a, negative 1).

We talked earlier about how the logarithmic function f-1(x) = logax is the inverse of the exponential function f(x) = ax. The graphs below show both the exponential (blue) and logarithmic (red) functions on the same graph for both a > 1 and 0 < a < 1.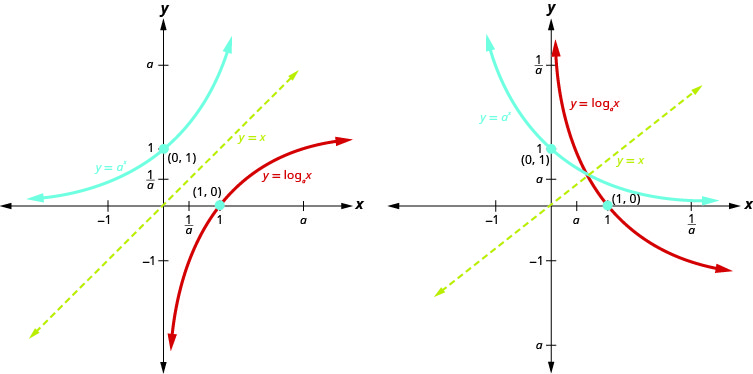This figure shows that, for a greater than 1, the logarithmic curve going through the points (1 over a, negative 1), (1, 0), and (a, 1). It also shows the exponential curve going through the points (1, 1 over a), (0, 1), and (1, a) along with the line y equals x. The logarithmic curve is a mirror image of the exponential curve across the y equals x line. This figure shows that, for a greater than 0 and less than 1, the logarithmic curve going through the points (a, 1), (1, 0), and (1 over a, negative 1). It also shows the exponential curve going through the points (negative 1, 1 over a), (0, 1), and (1, a) along with the line y equals x. The logarithmic curve is a mirror image of the exponential curve across the y equals x line.Notice how the graphs are reflections of each other through the line y = x. We know this is true of inverse functions.

Keeping a visual in your mind of these graphs will help you remember the domain and range of each function. Notice the x-axis is the horizontal asymptote for the exponential functions and the y-axis is the vertical asymptote for the logarithmic functions.

Natural and Common Logarithms

When we talked about exponential functions, we introduced the number e. Just as e was a base for an exponential function, it can be used a base for logarithmic functions too. The logarithmic function with base e is called the natural logarithmic function. The function f(x) = logex is generally written f(x) = ln x and we read it as “el en of x.”

Natural Logarithmic Function

The function f(x) = ln x is the natural logarithmic function with base e, where x > 0.

y = ln x is equivalent to x = ey 

We read ln(x) as, “the logarithm with base e of x” or “the natural logarithm of x.”

The logarithm y is the exponent to which e must be raised to get x.

Since the functions y = ex and y = ln(x) are inverse functions, ln(ex) = x for all x and e = x for x > 0.

Sometimes we may see a logarithm written without a base. In this case, we assume that the base is 10. In other words, the expression log(x) means log10(x). We call a base-10 logarithm a common logarithm function and the base is not shown.

Common Logarithmic Function

The function f(x) = log x is the common logarithmic function with base 10, where x > 0.

y = log(x) is equivalent to 10y = x

We read log(x) as, “the logarithm with base 10 of x” or “log base 10 of x.”

 

To solve logarithmic equations, one strategy is to change the equation to exponential form and then solve the exponential equation as we did before. As we solve logarithmic equations, y = logax, we need to remember that for the base a, a > 0 and a ≠ 1. Also, the domain is x > 0. Just as with radical equations, we must check our solutions to eliminate any extraneous solutions.

Given a common logarithm of the form y = log(x), evaluate it mentally.

  1. Rewrite the argument x as a power of 10: 10y = x.
  2. Use previous knowledge of powers of 10 to identify y by asking, “To what exponent must 10 be raised in order to get x?

Try it!

Solve: a. loga49 = 2 and b. ln x = 3.

Solution A (click to reveal)

 

a.

Steps Algebraic
Logarithm loga49 = 2
Rewrite in exponential form. a2 = 49
Solve the equation using the square root property. a = ±7
The base cannot be negative, so we eliminate a = −7. a = 7, a = −7
Check. a = 7 loga49 = 2
\displaystyle log_{7}49\stackrel{?}{=}2
\displaystyle 7^{2}\stackrel{?}{=}49
49 = 49✓

 

Solution B (click to reveal)

b.

Steps Algebraic
Logarithm ln x = 3
Rewrite in exponential form. e3 = x
Check. x = e3 ln x = 3
\displaystyle ln e^{3}\stackrel{?}{=}3
e3 = e3 ✓

 

Solve:

a. loga121 = 2 

b. ln x = 7

Solution (click to reveal)

a. a = 11
b. x = e7

 

 Solve:

a. loga64 = 3 

b. ln x = 9

Solution (click to reveal)

a. a = 4
b. x = e9

 

Solve:

a. log2(3x − 5) = 4

b. ln e2x = 4.

Solution A (click to reveal)

a.

Steps Algebraic
Equation log2(3x − 5) = 4
Rewrite in exponential form. 24 = 3x − 5
Simplify. 16 = 3x − 5
Solve the equation. 21 = 3x
Solution 7 = x
Check. x = 7 log2(3x − 5) = 4
\displaystyle log_{2}(3\cdot7-5)\stackrel{?}{=}4
\displaystyle log_{2}(16)\stackrel{?}{=}4
\displaystyle 2^{4}\stackrel{?}{=}16
16 = 16 ✓

 

Solution B (click to reveal)

b.

Steps Algebraic
Equation ln e2x = 4
Rewrite in exponential form. e4 = e2x
Since the bases are the same the exponents are equal. 4 = 2x
Solve the equation. 2 = x
Check. x = 2 ln e2x = 4
\displaystyle ln e^{2\cdot 2}\stackrel{?}{=}4
\displaystyle ln e^{4}\stackrel{?}{=}4
e4 = e4 ✓

 

 Solve:

a. log2(5x − 1) = 6 

b. ln e3x = 6

Solution (click to reveal)

a. x = 13
b. x = 2

 

 Solve:

a. log3(4x + 3) = 3 

b. ln e4x = 4

Solution C (click to reveal)

a. x = 6
b. x = 1

 

Applications with Logarithms

There are many applications that are modeled by logarithmic equations. We will first look at the logarithmic equation that gives the decibel (dB) level of sound. Decibels range from 0, which is barely audible to 160, which can rupture an eardrum.

The 10-12 in the formula represents the intensity of sound that is barely audible.

Decibel Level of Sound

The loudness level, D, measured in decibels, of a sound of intensity, I, measured in watts per square inch is

\displaystyle D=10 log\left(\frac{I}{10^{-12}}\right)

Try it!

Extended exposure to noise that measures 85 dB can cause permanent damage to the inner ear which will result in hearing loss. What is the decibel level of music coming through earphones with intensity 10-2 watts per square inch?

Solution (click to reveal)
Steps Algebraic
Equation We start with D equals 10 times log of the quantity I over 10 to the negative 12 power.
Substitute in the intensity level, I. We substitute in the intensity level I to obtain D equals 10 log of the quantity10 to the negative 2 power over 10 to the negative 12 power.
Simplify. We then simplify to obtain D equals 10 times log of 10 to the 10 power.
Since log 1010 = 10. Since log of 10 to the 10 equals 10, we have that D equals 10 times 10.
Multiply. Multiplying gives that D equals 100. Hence, the decibel level of music coming through earphones is 100 dB.

The decibel level of music coming through earphones is 100 dB.

What is the decibel level of one of the new quiet dishwashers with intensity 10-7 watts per square inch?

Solution (click to reveal)

The quiet dishwashers have a decibel level of 50 dB.

 

 The magnitude R of an earthquake is measured by a logarithmic scale called the Richter scale. The model is R = log I, where I is the intensity of the shock wave. This model provides a way to measure earthquake intensity.
Earthquake Intensity

The magnitude R of an earthquake is measured by R = log I, where I is the intensity of its shock wave.

Try it!

In 1906, San Francisco experienced an intense earthquake with a magnitude of 7.8 on the Richter scale. Over 80% of the city was destroyed by the resulting fires. In 2014, Los Angeles experienced a moderate earthquake that measured 5.1 on the Richter scale and caused $108 million dollars of damage. Compare the intensities of the two earthquakes.

Solution (click to reveal)

To compare the intensities, we first need to convert the magnitudes to intensities using the log formula. Then we will set up a ratio to compare the intensities.

Steps Algebraic
Convert the magnitudes to intensities.  R = log I
1906 earthquake 7.8 = log I
Convert to exponential form. I = 107.8
2014 earthquake 5.1 = log I
Convert to exponential form. I = 105.1
Form a ratio of the intensities. \displaystyle\frac{\text{Intensity for }1906}{\text{Intensity for }2014}
Substitute in the values. \displaystyle\frac{10^{7.8}}{10^{5.1}}
Divide by subtracting the exponents. 102.7
Evaluate. 501

The intensity of the 1906 earthquake was about 501 times the intensity of the 2014 earthquake.

Key Concepts

  • Log definitions
    Term Definition
    Definition of the logarithmic function For x > 0, b > 0, b ≠ 1, 

    y = logb(x) if and only if by = x.
    Definition of the common logarithm For x > 0, y = log(x) if and only if 10y = x.
    Definition of the natural logarithm For x > 0, y = ln(x) if and only if ey = x.
  • Properties of the Graph of y = logax:
    when a > 1 when 0 < a < 1
    Domain (0, ∞) Domain (0, ∞)
    Range (−∞, ∞) Range (−∞, ∞)
    x-intercept (1, 0) x-intercept (1, 0)
    y-intercept none y-intercept none
    Contains (a, 1), 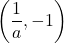\displaystyle\left(\frac{1}{a},-1\right) Contains (a, 1), 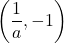\displaystyle\left(\frac{1}{a},-1\right)
    Asymptote y-axis Asymptote y-axis
    Basic shape increasing Basic shape decreasing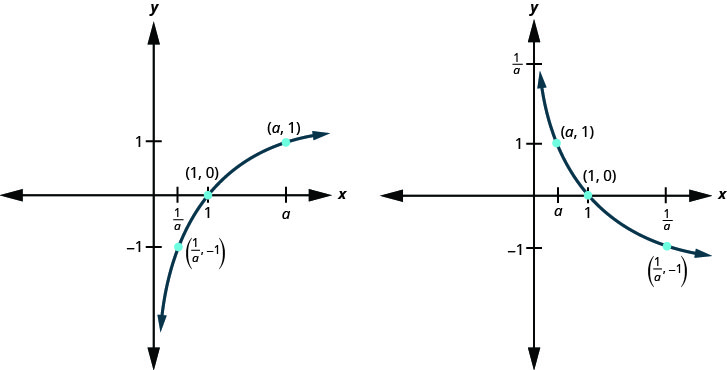

    This figure shows that, for a greater than 1, the logarithmic curve going through the points (1 over a, negative 1), (1, 0), and (a, 1). This figure shows that, for a greater than 0 and less than 1, the logarithmic curve going through the points (a, 1), (1, 0), and (1 over a, negative 1).

  • Decibel Level of Sound: The loudness level,
    D, measured in decibels, of a sound of intensity, I, measured in watts per square inch is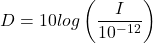 \displaystyle D=10log\left(\frac{I}{10^{-12}}\right).
  • Earthquake Intensity: The magnitude
    R of an earthquake is measured by R = log I, where I is the intensity of its shock wave.
  1. Derived from Openstax College Algebra 2e with Corequisite supports, Access for free at https://openstax.org/books/college-algebra-corequisite-support-2e/pages/1-introduction-to-prerequisites . Intermediate Algebra, Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0572 Corequisite Support Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book