"

16 Proportions

Topics Covered[1]

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

Use the Definition of Proportion[2]

In the section on Ratios and Rates we saw some ways they are used in our daily lives. When two ratios or rates are equal, the equation relating them is called a proportion.

Proportion

A proportion is an equation of the form \displaystyle\frac{a}{b}= \frac{c}{d} where b ≠ 0, d ≠ 0. The proportion states two ratios or rates are equal. The proportion is read “a is to b, as c is to d.”

The equation \displaystyle \frac{1}{2} = \frac{4}{8} is a proportion because the two fractions are equal. The proportion \displaystyle \frac{1}{2} = \frac{4}{8} is read “1 is to 2 as 4 is to 8”.

If we compare quantities with units, we have to be sure we are comparing them in the right order. For example, in the proportion \displaystyle \frac{20 \text{ students}}{1 \text{ teacher}} = \frac{60 \text{ students}}{3 \text{ teachers}} we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.

Try it!

  1. a. 3 is to 7 as 15 is to 35.
  2. b. 5 hits in 8 at-bats is the same as 30 hits in 48 at-bats.
  3. c. $1.50 for 6 ounces is equivalent to $2.25 for 9 ounces.

    Solution

    a.

    Steps Algebraic
    3 is to 7 as 15 is to 35.
    Write as a proportion. \displaystyle \frac{3}{7} = \frac{15}{35}

    b.

    Steps Algebraic
    5 hits in 8 at-bats is the same as 30 hits in 48 at-bats.
    Write each fraction to compare hits to at-bats.  hits at-bats = hits at-bats
    Write as a proportion. \displaystyle \frac{5}{8} = \frac{30}{48}

    c.

    Steps Algebraic
    $1.50 for 6 ounces is equivalent to $2.25 for 9 ounces.
    Write each fraction to compare dollars to ounces. \displaystyle \frac{\$}{\text{ounces}} = \frac{\$}{\text{ounces}}
    Write as a proportion. \displaystyle \frac{\$1.50}{6} = \frac{\$2.25}{9}

    Using and Applying Proportional Relationships to Solve Problems[3]

    Using proportions to solve problems is a very useful method. It is usually used when you know three parts of the proportion, and one part is unknown. Proportions are often solved by setting up like ratios. If \displaystyle \frac{a}{b} and \displaystyle \frac{c}{d} are two ratios such that \displaystyle \frac{a}{b} = \frac{c}{d}, then the fractions are said to be proportional. Also, two fractions \displaystyle \frac{a}{b} and \displaystyle \frac{c}{d} are proportional \displaystyle \left(\frac{a}{b} = \frac{c}{d} \right) if and only if a \times d = b \times c.

    Look at the proportions \displaystyle \frac{1}{2} = \frac{4}{8} and \displaystyle \frac{2}{3} = \frac{6}{9}. From our work with equivalent fractions, we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?

    To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross product because of the cross formed. If, and only if, the given proportion is true, that is, the two sides are equal, then the cross products of a proportion will be equal.

    The figure shows cross multiplication of two proportions. There is the proportion 1 is to 2 as 4 is to 8. Arrows are shown diagonally across the equal sign to show cross products. The equations formed by cross multiplying are 8 · 1 = 8 and 2 · 4 = 8. There is the proportion 2 is to 3 as 6 is to 9. Arrows are shown diagonally across the equal sign to show cross products. The equations formed by cross multiplying are 9 · 2 = 18 and 3 · 6 = 18.

    Cross Products of a Proportion

    For any proportion of the form \displaystyle \frac{a}{b} = \frac{c}{d}, where b \neq 0, d \neq 0, its cross products are equal.No Alt Text

     

    Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are both equal, we have a proportion.

    To solve a proportion containing a variable, we remember that the proportion is an equation. All of the techniques we have used so far to solve equations still apply. In the next example, we will solve a proportion by multiplying by the Least Common Denominator (LCD) using the Multiplication Property of Equality.

    Try it!

    Solve: \displaystyle \frac{x}{63} = \frac{4}{7}

    Solution

    Steps Algebraic
    \displaystyle \frac{x}{63} = \frac{4}{7}
    To isolate x, multiply both sides by the LDC, 63. \displaystyle \textcolor{red}{63} \left(\frac{x}{63} \right) = \textcolor{red}{63} \left(\frac{4}{7} \right)
    Simplify. \displaystyle x = \frac{9 \cdot \cancel{7} \cdot 4}{\cancel{7}}
    Divide the common factors. \displaystyle x = 36
    Check: To check our answer, we substitute into the original proportion.
    \displaystyle \frac{x}{63} = \frac{4}{7}
    substitute x = \textcolor{red}{36} \displaystyle \frac{\textcolor{red}{36}}{63} \stackrel{?}{=} \frac{4}{7}
    Show common factors. \displaystyle \frac{4 \cdot 9}{7 \cdot 9} \stackrel{?}{=} \frac{4}{7}
    Simplify. \displaystyle \frac{4}{7} = \frac{4}{7} \checkmark

     

    When the variable is in a denominator, we’ll use the fact that the cross products of a proportion are equal to solve the proportions.

    We can find the cross products of the proportion and then set them equal. Then we solve the resulting equation using our familiar techniques.

    Try it!

    Solve: \displaystyle\frac{114}{a} = \frac{9}{4}

    Solution

    Notice that the variable is in the denominator, so we will solve by finding the cross products and setting them equal.

    Steps Algebraic
    .
    Find the cross products and set them equal. 4 \cdot 144 = a \cdot 9
    Simplify. 576 = 9a
    Divide both sides by 9. \displaystyle \frac{576}{9} = \frac{9a}{9}
    Simplify. 64 = a
    Check your answer.
    \displaystyle \frac{144}{a} = \frac{9}{4}
    substitute a = 64
    		 \displaystyle \frac{144}{\textcolor{red}{64}} \stackrel{?}{=} \frac{9}{4}
    Show common factors. \displaystyle \frac{9 \cdot 16}{4 \cdot 16} \stackrel{?}{=} \frac{9}{4}
    Simplify. \displaystyle \frac{9}{4} = \frac{9}{4} \checkmark

    Another method to solve this would be to multiply both sides by the LCD, 4a. Try it and verify that you get the same solution.

    Write Percent Equations as Proportions

    Previously, we solved percent equations by applying the properties of equality we have used to solve equations throughout this text. Some people prefer to solve percent equations by using the proportion method. The proportion method for solving percent problems involves a percent proportion. A percent proportion is an equation where a percent is equal to an equivalent ratio.

    For example, \displaystyle 60\% = \frac{60}{100}, and we can simplify \displaystyle \frac{60}{100} = \frac{3}{5}. Since the equation \displaystyle \frac{60}{100} = \frac{3}{5} shows a percent equal to an equivalent ratio, we call it a percent proportion. Using the vocabulary we used earlier:

    \displaystyle \frac{\text{amount}}{\text{base}} = \frac{\text{percent}}{{100}}

    \displaystyle \frac{3}{5} = \frac{60}{100}

    Percent Proportion

    The amount is to the base as the percent is to 100.

    \displaystyle \frac{\text{amount}}{\text{base}} = \frac{\text{percent}}{{100}}

    If we restate the problem in the words of a proportion, it may be easier to set up the proportion:  The amount is to the base as the percent is to one hundred.

    We could also say: The amount out of the base is the same as the percent out of one hundred.

    We will practice translating into a percent proportion.

    Try it!

    Translate to a proportion. What number is 75% of 90?

    Solution

    If you look for the word “of,” it may help you identify the base.

    Steps Algebraic
    Identify the parts of the percent proportion. .
    Restate as a proportion. .
    Set up the proportion. Let n = number. \displaystyle \frac{n}{90} = \frac{77}{100}

    Key Concepts

    • A proportion is an equation of the form 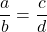\displaystyle \frac{a}{b} = \frac{c}{d}, where b\neq 0,d \neq 0.
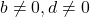    • Percent Proportion
      • \displaystyle \frac{\text{amount}}{\text{base}} = \frac{\text{percent}}{{100}}
    1. Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ;Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction ↵
    2. Derived from Openstax Pre-Algebra: Percents - Solve Proportions and their application ↵
    3. Conetnt derived from Openstax PreAlgebra: Percents - Solve Proportions and their application and Contemporary math: Algebra- Ratios and Proportions ↵

    License

    Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

    NCB 0542 Corequisite Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

    Share This Book