14 Solving Applications Involving Percentages
Topics Covered[1]
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
Calculate the Total, Percent, or Part[2]
So, to calculate “25% of 52,” we multiply 52 by 25%. But, first we need to convert the percent to either fractional form (25/100) or decimal form. Using the decimal form of 25% we have 0.25 × 52, which equals 13.
In this problem, 52 is the total or base, 25 is the percentage, and 13 is the percentage of 52, or the part of 52. This is sometimes referred to as the amount.
Formula
The mathematical formula relating the total (base), the percent in decimal form, and the part (amount) is
part = percent x total, or amount = percent x base.
Knowing any two of the values in our formula allows us to calculate the third value. In the following example, we know the total and the percent, and are asked to find the percentage of the total.
Try it! – Finding the Percent of a Total
- Determine 70% of 3,500
- Determine 156% of 720
Solution
- The total is x = 3,500, and the percent is n = 70. The decimal form of 70% is 0.70. To find the part, or percent of the total, substitute those values into the formula and calculate. part = percent x total = 0.070 x 3500 = 2450. For this, we say that 70% of 3,500 is 2,450.
- The total is x = 720, and the percent is n = 156. The decimal form of 156% is 1.56. To find the part, or percent of the total, substitute those values into the formula and calculate. part = percent x total = 1.56 x 720 = 1,123.2.
In the previous example, we knew the total and the percent and found the part using our formula. We may instead know the percent and the part, but not the total. We can use our formula again to solve for the total.
Try it! – Finding the Total from the Percent and the Part
- What is the total if 35% of the total is 70?
- What is the total if 10% of the total is 4,000?
Solution
1.
Step 1: The percent is 35, which in decimal form is 0.35. We were given that 35% of the total is 70, so the part is 70. We are to find the total. Substituting into the formula, we have 70 = 0.35 x total
Step 2: To find the total, we solve the equation for the total,
total = 70/0.35 = 200
From this we see that 200 is the total, or, that 35% of 200 is 70.
2.
Step 1: The percent is 10, which in decimal form is 0.1. We were given that 10% of the total is 4,000, so the part is 4,000. Substituting into the formula, we have 4000 = 0.1 x total.
Step 2: To find the total, we solve the equation for the total.
total = 4000/0.1 = 40,000
From this we see that 40,000 is the total, or that 10% of 40,000 is 4,000.
Solve Applications of Percent[3]
Many applications of percent occur in our daily lives, such as tips, sales tax, discount, and interest. To solve these applications we’ll translate to a basic percent equation, just like those we solved in the previous examples in this section. Once you translate the sentence into a percent equation, you know how to solve it.
We will update the strategy we used in our earlier applications to include equations now. Notice that we will translate a sentence into an equation.
How To:
Solve an application
- Step 1. Identify what you are asked to find and choose a variable to represent it.
- Step 2. Write a sentence that gives the information to find it.
- Step 3. Translate the sentence into an equation.
- Step 4. Solve the equation using good algebra techniques.
- Step 5. Check the answer in the problem and make sure it makes sense.
- Step 6. Write a complete sentence that answers the question.
Now that we have the strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we’ll solve involve everyday situations, you can rely on your own experience.
Try it!
Dezohn and his girlfriend enjoyed a dinner at a restaurant, and the bill was $68.50. They want to leave an 18% tip. If the tip will be 18% of the total bill, how much should the tip be?
Solution
| Steps | Algebraic |
| What are you asked to find? | the amount of the tip |
| Choose a variable to represent it. | Let t = amount of tip. |
| Write a sentence that give the information to find it. | The tip is 18% of the total bill. |
| Translate the sentence into an equation. | |
| Multiply. | |
| Check. Is this answer reasonable? | |
| If we approximate the bill to $70 and the percent to 20%, we would have a tip of $14. So a tip of $12.33 seems reasonable. |
|
| Write a complete sentence that answers the question. | The couple should leave a tip of $12.33. |
Calculating Discounts[4]
Retailers frequently hold sales to help move merchandise. When you buy an item on sale, the original price of the item has been reduced by some dollar amount. These are discounts, a reduction in the price of something. The discount rate, usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount, we multiply the discount rate by the original price. We summarize the discount model in the box below.
When a reduction is a percent discount, it is an application of percent. The formula used was ![]() . In a discount application, the discount plays the role of the part, the percent discount is the percentage, and the original price plays the role of the total.
. In a discount application, the discount plays the role of the part, the percent discount is the percentage, and the original price plays the role of the total.
Discount:
An amount of discount is a percent off the original price.
amount of discount = discount rate x original price
sale price = original price – discount
The sale price should always be less than the original price. In some cases, the amount of discount is a fixed dollar amount. Then we just find the sale price by subtracting the amount of discount from the original price.
Try it!
#1
Jason bought a pair of sunglasses that were on sale for $10 off. The original price of the sunglasses was $39. What was the sale price of the sunglasses?
Solution
| Steps | Algebraic |
| Identify what you are asked to find. | What is the sale price? |
| Choose a variable to represent it. | Let s = the sales price |
| Write a sentence that gives the information to find it. | The sale price is the original price minus the discount. |
| Translate into an equation. | |
| Simplify. | |
| Check if this answer is reasonable. | |
| Yes. The sale price, $29, is less than the original price, $39. | |
| Write a complete sentence that answers the question. | The sale price of the sunglasses was $29. |
#2
Elise bought a dress that was discounted 35% off of the original price of $140. What was
a. the amount of the discount
b. the sale price of the dress?
Solution
a.
Before beginning, you may find it helpful to organize the information in a list.
Original price = $140
Discount rate = 35%
Amount of discount = ?
| Steps | Algebraic |
| Identify what you are asked to find. | What is the amount of discount? |
| Choose a variable to represent it. | Let d = the amount of the discount. |
| Write a sentence that gives the information to find it. | The discount is 35% of the original price. |
| Translate into an equation. | |
| Simplify. | |
| Check if this answer is reasonable. | |
| Yes. A $49 discount is reasonable for a $140 dress. | |
| Write a complete sentence that answers the question. | The amount of discount was $49. |
Original price = $140
Amount of discount = $49
Sale price = ?
| Steps | Algebraic |
| Identify what you are asked to find. | What is the sale price of the dress? |
| Choose a variable to represent it. | Let s = the sale price. |
| Write a sentence that gives the information to find it. | The sale price is the original price minus the discount. |
| Translate into an equation. | |
| Simplify. | |
| Check if this answer is reasonable. | |
| Yes. The sale price, $91, is less than the original price, $140. | |
| Write a complete sentence that answers the question. | The sale price of the dress was $91. |
Solve Sales Tax Applications
Sales tax and commissions are applications of percent in our everyday lives. To solve these applications, we will follow the same strategy we used in the section on decimal operations. We show it again here for easy reference.
How To:
Solve an application
- Step 1. Identify what you are asked to find and choose a variable to represent it.
- Step 2. Write a sentence that gives the information to find it.
- Step 4. Solve the equation using good algebra techniques.
- Step 5. Check the answer in the problem and make sure it makes sense.
- Step 6. Write a complete sentence that answers the question.
Remember that whatever the application, once we write the sentence with the given information (Step 2), we can translate it to a percent equation and then solve it.
Do you pay a tax when you shop in your city or state? In many parts of the United States, sales tax is added to the purchase price of an item. See the image below.
The sales tax is determined by computing a percent of the purchase price.
To find the sales tax multiply the purchase price by the sales tax rate. Remember to convert the sales tax rate from a percent to a decimal number. Once the sales tax is calculated, it is added to the purchase price. The result is the total cost—this is what the customer pays.
Sales Tax
The sales tax is a percent of the purchase price.
![]()
![]()
Try it!
#1
Cathy bought a bicycle in Washington, where the sales tax rate was 6.5% of the purchase price. What was
a. the sales tax and
b. the total cost of a bicycle if the purchase price of the bicycle was $392?
Solution
a.
| Steps | Algebraic |
| Identify what you are asked to find. | What is the sales tax? |
| Choose a variable to represent it. | Let t = sales tax |
| Write a sentence that gives the information to find it. | The sales tax is 6.5% of the purchase price. |
| Translate into an equation. (Remember to change the percent to a decimal). | |
| Simplify. | |
| Check: Is this answer reasonable? | |
| Yes, because the sales tax amount is less than 10% of the purchase price. | |
| Write a complete sentence that answers the question. | The sales tax is $25.48. |
b.
| Steps | Algebraic |
| Identify what you are asked to find. | What is the total cost of the bicycle? |
| Choose a variable to represent it. | Let c = total cost of bicycle |
| Write a sentence that gives the information to find it. | The total cost is the purchase price plus the sales tax. |
| Translate into an equation. | |
| Simplify. | |
| Check: Is this answer reasonable? | |
| Yes, because the total cost is a little more than the purchase price. | |
| Write a complete sentence that answers the question. | The total cost of the bicycle is $417.48. |
#2
Evelyn bought a new smartphone for $499 plus tax. She was surprised when she got the receipt and saw that the tax was $42.42. What was the sales tax rate for this purchase?
Solution
| Steps | Algebraic |
| Identify what you are asked to find. | What is the sales tax rate? |
| Choose a variable to represent it. | Let r = sales tax |
| Write a sentence that gives the information to find it. | What percent of the price is the sales tax? |
| Translate into an equation. | |
| Divide. | |
| Simplify. | |
| Check. Is this answer reasonable? | |
| Yes, because 8.5% is close to 10%. 10% of $500 is $50, which is close to $42.42. |
|
| Write a complete sentence that answers the question. | The sales tax rate is 8.5%. |
Key Concepts
- Formula for Calculating total/percent/part:
- part = percent x total, or amount = percent x base.
- Solving Percent applications
- Step 1. Identify what you are asked to find and choose a variable to represent it.
- Step 2. Write a sentence that gives the information to find it.
- Step 3. Translate the sentence into an equation.
- Step 4. Solve the equation using good algebra techniques.
- Step 5. Check the answer in the problem and make sure it makes sense.
- Step 6. Write a complete sentence that answers the question.
- Amount of discount = discount rate x original price & sale price = original price – discount
- Sales Tax
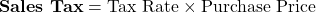 [latex]\textbf{Total Cost} = \text{Purchase Price} + \text{Sales Tax}[/latex]
[latex]\textbf{Total Cost} = \text{Purchase Price} + \text{Sales Tax}[/latex]
- Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ; Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction ↵
- Section derived from Openstax: Contemporary math, Money management - Understanding percentages ↵
- derived from Openstax Pre-algebra: Percents - solve general applications of percents ↵
- Derived from Openstax Contemporary math- money matters, discounts/markups and Pre-algebra Percents: Solve sales tax, commision and discount ↵

