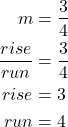20 More on Slope and Equations
Topics Covered:[1]
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
Slope and Equations
Now that we’ve defined slope and looked at the Standard form of a line (Ax + By = C), there are two other forms of a linear equation in addition to the Standard form:
| Point Slope Form | Slope Intercept Form |
| y − y1 = m(x − x1) | y = mx + b |
| where m=slope (x1,y1) is a point on the line. | where m = slope and b = y-intercept. |
What if all you are given is 2 points of a line? We know from the previous section that you could use them to determine slope, but this process will also allow us to find out what the linear equation would look like.
Slope also indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.
Suppose we have a line that has slope m and that contains some specific point (x1,y1) and some other point, which we will just call (x,y). We can write the slope of this line and then change it to a different form.
| Steps | Algebraic |
| Equation | m = |
| Multiply both sides of the equation by x − x1. | m(x – x1) = |
| Simplify. | m(x – x1) = y – y1 |
| Rewrite the equation with the y terms on the left. | y – y1 = m(x – x1) |
Given one point and the slope, the point-slope formula will lead to the equation of a line:
What happens if you only have two points? Can we find the slope with just two points? Yes, using the steps we looked at in the previous section. Once we have the slope, we can use it and one of the given points to find the equation. The following example gives two points, so you need to solve for the slope first and then use one of the points.
How to find the equation with 2 Points:
- Find the slope using the given points. m =
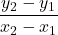
- Choose one point.
- Substitute the values into the point-slope form: y − y1 = m (x − x1)
- Write the equation in slope-intercept form.
Try it!
Find the equation of the line passing through the points (3,4) and (0,−3). Write the final equation in slope-intercept form.
Solution (click to reveal)
First, we calculate the slope using the slope formula and two points.
Next, we use the point-slope formula with the slope of ![]() , and either point. Let’s pick the point (3,4) for (x1,y1).
, and either point. Let’s pick the point (3,4) for (x1,y1).
The equation is written as y = ![]() – 3. (This is known as the Slope-intercept form.)
– 3. (This is known as the Slope-intercept form.)
Analysis
To prove that either point can be used, let us use the second point (0,−3) and see if we get the same equation.
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.
Find an equation of a line that contains the points (−3,5) and (−3,4). Write the equation in slope-intercept form.
Solution (click to reveal)
Again, the first step will be to find the slope.
m = ![]()
m = ![]()
m = ![]()
The Slope is undefined.
This tells us it is a vertical line. Both of our points have an x-coordinate of −2. So our equation of the line is x = −2. Since there is no y, we cannot write it in slope-intercept form.
You may want to sketch a graph using the two given points. Does your graph agree with our conclusion that this is a vertical line?
Try it! – How to Find the Equation of a Line Given Two Points
Find an equation of a line that contains the points (−3,−1) and (2,−2). Write the equation in slope-intercept form.
Solution (click to reveal)
| Steps | Algebraic |
| Step 1. Find the slope using the given points
Find the slope of the line through (-3, -1) and (2, -2). |
|
| Step 2. Choose one point. Choose either point. | |
| Step 3. Substitute the values into the point-slope form, Simplify. |
|
| Step 4. Write the equation in slope-intercept form. |
In the examples above, you will note that the form of the equation we get after using point-slope form is: y = mx+b. where m=slope and b = y-intercept. Practice identifying them below.
Try it! – Identifying the Slope and y-intercept of a Line Given an Equation
Identify the slope and y-intercept, given the equation y = –![]() – 4
– 4
Solution (click to reveal)
As the line is in y = mx+b form, the given line has a slope of m = ![]() . The y-intercept is b = −4.
. The y-intercept is b = −4.
The y-intercept is the point at which the line crosses the y-axis. On the y-axis, x=0. We can always identify the y-intercept when the line is in slope-intercept form, as it will always equal b. Or, just substitute x=0 and solve for y.
We can easily determine the slope and intercept of a line if the equation is written in slope-intercept form, y = mx+b. Now we will do the reverse—we will start with the slope and y-intercept and use them to find the equation of the line.
How To: Find the equation given a slope and a point
- Identify the slope.
- Identify the point.
- Substitute the values into the point-slope form, y − y1 = m(x − x1).
- Write the equation in slope-intercept form.
Try it! – Finding the Equation of a Line Given the Slope and One Point
Write the equation of the line with slope m = −3 and passing through the point (4,8). Then solve the equation for y.
Solution (click to reveal)
Using the point-slope formula, substitute −3 for m and the point (4,8) for (x1,y1).
Note that any point on the line can be used to find the equation. If done correctly, the same final equation will be obtained.
Find the equation of a line with slope m = –![]() and containing the point (10, −5).
and containing the point (10, −5).
Solution (click to reveal)
y = –![]() – 1
– 1
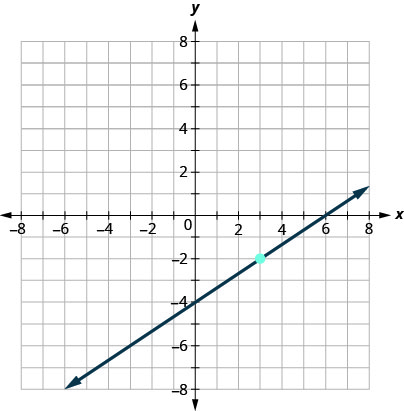
Find the equation of the line shown in the graph.
Solution (click to reveal)
We need to find the slope and y-intercept of the line from the graph so we can substitute the needed values into the slope-intercept form, y=mx+b
To find the slope, we choose two points on the graph.
The y-intercept is (0,−4) and the graph passes through (3,−2).
| Steps | Algebraic |
| Find the slope by counting the rise and run. |
|
| Use the graph to identify the points and count. | |
| Find the y-intercept. | |
| Substitute the values into y=mx+b | |
| Solution |
Find an equation of a horizontal line that contains the point (−2,−6). Write the equation in slope-intercept form.
Solution (click to reveal)
Every horizontal line has slope 0. We can substitute the slope and points into the point-slope form, y − y1 = m(x − x1).
| Steps | Algebraic |
| Identify the slope. |
|
| Identify the point. | |
| Substitute the values into
y − y1 = m(x − x1) |
|
| Simplify. |
|
| Write in slope-intercept form. | It is in y-form, but could be written y = 0x − 6. |
Did we end up with the form of a horizontal line, y = a?
Graphing and Slope
We can also graph a line when we know one point and the slope of the line. We will start by plotting the point and then use the definition of slope to draw the graph of the line.
Try it! – How to graph a Line Given a Point and the Slope
Graph the line passing through the point (1,−1) whose slope is m = ![]() .
.
Solution (click to reveal)
| Steps | Algebraic |
| Plot the given point (1, -1). | 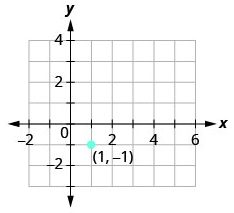 |
| Use the slope formula |
|
| Starting at the given point (1, -1), count out the rise ( up 3 units) and run (right 4 units) to mark the second point. | 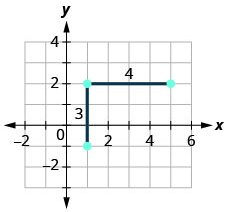 |
| Connect the two points with a line. | 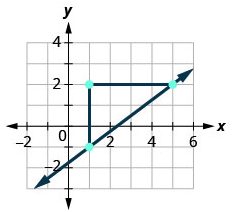 |
You can check your work by finding a third point. Since the slope is m = ![]() it can also be written as m =
it can also be written as m = ![]() (negative divided by negative is positive!). Go back to (1,−1) and count out the rise, −3, and the run, −4.
(negative divided by negative is positive!). Go back to (1,−1) and count out the rise, −3, and the run, −4.
Graph the line passing through the point (2,−2) with the slope m = ![]()
Solution (click to reveal)
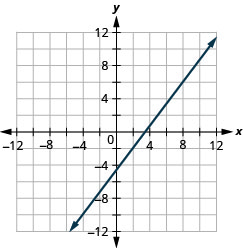
Graph the line passing through the point (−2,3) with the slope m = ![]()
Solution (click to reveal)
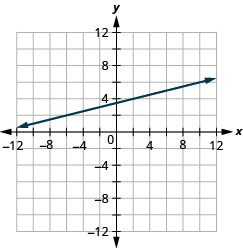
- Plot the given point.
- Use the slope formula m =
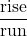 to identify the rise and the run.
to identify the rise and the run. - Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
Graphing with Slope and Intercept
We have graphed linear equations by plotting points, using intercepts, recognizing horizontal and vertical lines, and using one point and the slope of the line. Once we see how an equation in slope–intercept form and its graph are related, we’ll have one more method we can use to graph lines.
Let’s look at the graph of the equation y = ![]() + 3 and find its slope and y-intercept.
+ 3 and find its slope and y-intercept.
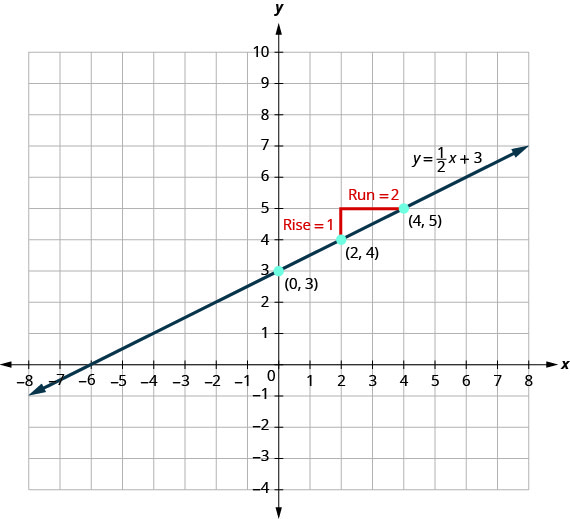
The red lines in the graph show us that the rise is 1 and the run is 2. Substituting into the slope formula:
The y-intercept is (0,3). Look at the equation of this line:
Look at the slope and y-intercept.
![]()
When a linear equation is solved for y, the coefficient of the x term is the slope, and the constant term is the y-coordinate of the y-intercept. We say that the equation y = ![]() + 3 is in slope–intercept form. Sometimes the slope–intercept form is called the “y-form.”
+ 3 is in slope–intercept form. Sometimes the slope–intercept form is called the “y-form.”
![]()
Let’s practice finding the values of the slope and y-intercept from the equation of a line.
Try It!
Identify the slope and y-intercept of the line from the equation:
a. y = −![]() − 2
− 2
b. x + 3y = 9
Solution A (click to reveal)
a. We compare our equation to the slope–intercept form of the equation.
| Steps | Algebraic |
| Write the slope–intercept form of the equation of the line. |
|
| Write the equation of the line. |
|
| Identify the slope. | |
| Identify the y-intercept. |
Solution B (click to reveal)
b. When an equation of a line is not given in slope–intercept form, our first step will be to solve the equation for y.
| Steps | Algebraic |
| Solve for y. |
|
| Subtract x from each side. | |
| Divide both sides by 3. | |
| Simplify. | |
| Write the slope–intercept form of the equation of the line. | |
| Write the equation of the line. | |
| Identify the slope. | |
| Identify the y-intercept. |
|
Identify the slope and y-intercept from the equation of the line.
a. y = −![]() + 1
+ 1
b. 3x+2y=12
Solution (click to reveal)
a. m = −![]() ; (0, 1)
; (0, 1)
b. m = −![]() ; (0, 6)
; (0, 6)
We have graphed a line using the slope and a point. Now that we know how to find the slope and y-intercept of a line from its equation, we can use the y-intercept as the point, and then count out the slope from there.
Graph the line of the equation y = −x + 4 using its slope and y-intercept.
Solution (click to reveal)
| Steps | Algebraic |
| Equation | y = mx + b |
| The equation is in slope–intercept form. | y = −x + 4 |
| Identify the slope and y-intercept. | m = −1 y-intercept is (0, 4) |
| Plot the y-intercept. | See the graph. |
| Identify the rise over the run. | m = |
| Count out the rise and run to mark the second point. Draw the line as shown in the graph. | rise −1, run 1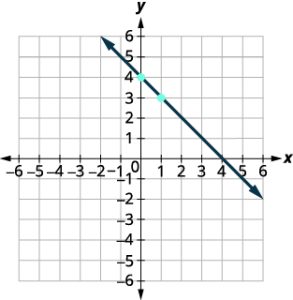 |
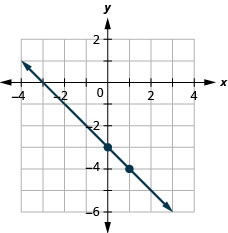
Graph the line of the equation y = −x − 3 using its slope and y-intercept.
Solution (click to reveal)
| Point-Plotting | Slope-Intercept | Intercepts | Recognize Vertical and Horizontal Lines |
| Create a blank table with two columns and four rows. The first row is labeled “x” and “y”. Find three points. Plot the points, make sure they line up, them draw the line. | y = mx + b
Find the slope and y-intercept, Start at the y-intercept, then count the slope to get a second point. |
Create a blank table with two columns and four rows. The first row is labeled “x” and “y”. Plug a zero in the first row in the x column. In the second row there is a 0 in the y column.
Find the intercepts and a 3rd point. Plot the points, make sure they line up, then draw the line.
|
The equation has only one variable.
x = a vertical. y = b horizontal. |
Key Concepts
- Slope of a line between two points.
- The slope of the line between two points (x1, y1) and (x2, y2) is:
m =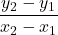
- The slope of the line between two points (x1, y1) and (x2, y2) is:
- How to graph a line given a point and the slope.
- Plot the given point.
- Use the slope formula m =
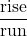 to identify the rise and the run.
to identify the rise and the run. - Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
- Slope Intercept Form of an Equation of a Line
-
- The slope–intercept form of an equation of a line with slope m and y-intercept, (0, b) is y = mx + b
- The slope–intercept form of an equation of a line with slope m and y-intercept, (0, b) is y = mx + b
Point-Plotting Slope-Intercept Intercepts Recognize Vertical and Horizontal Lines Create a blank table with two columns and four rows. The first row is labeled “x” and “y”. Find three points. Plot the points, make sure they line up, them draw the line. y = mx + b Find the slope and y-intercept, Start at the y-intercept, then count the slope to get a second point.
Create a blank table with two columns and four rows. The first row is labeled “x” and “y”. Plug a zero in the first row in the x column. In the second row there is a 0 in the y column. Find the intercepts and a 3rd point. Plot the points, make sure they line up, then draw the line.
The equation has only one variable. x = a vertical.
y = b horizontal.
We have seen that we can use either the slope-intercept form or the point-slope form to find an equation of a line. Which form we use will depend on the information we are given.
To Write an Equation of a Line If given: Use: Form: Slope and y-intercept slope-intercept y = mx + b Slope and a point point-slope y − y1 = m(x − x1) Two points point-slope y − y1 = m(x − x1) -
- Derived from Openstax Elementary Algebra, Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction. Intermediate Algebra, Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction. ↵