Unit Rates and Conversions:

Elizabeth Pople

12 Unit Rates and Conversions:

Topics Covered^[1]

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

Rate as a Fraction
Ratio of Two Measurements in Different Units
Find Unit Rates
Unit Conversions in US
Unit Conversions in Metric
Convert Between US and Metric
Key Concepts

In this section, we will see how to convert among different types of units, such as feet to miles or kilograms to pounds. The basic idea in all of the unit conversions will be to use a form of 1, the multiplicative identity, to change the units but not the value of a quantity.

Write a Rate as a Fraction ^[2]

Frequently we want to compare two different types of measurements, such as miles to gallons. To make this comparison, we use a rate. Examples of rates are 120 miles in 2 hours, 160 words in 4 minutes, and $5 dollars per 64 ounces.

A rate compares two quantities of different units. A rate is usually written as a fraction.

When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator.

Try it! – Writing Rate as a Fraction

Bob drove his car 525 miles in 9 hours. Write this rate as a fraction.

Solution

Step

Conversion

Write as a fraction, with 525 miles in the numerator and 9 hours in the denominator.

525 miles in 9 hours

$\displaystyle \frac{525 \, \text{miles}}{9 \,\text{hours}}$

$\displaystyle \frac{175 \,\text{miles}}{3 \,\text{hours}}$

So 525 miles in 9 hours is equivalent to $$\displaystyle \frac{175 \, \text{miles}}{3\, \text{hours}}$ .

Ratios of Two Measurements in Different Units ^[3]

To find the ratio of two measurements, we must make sure the quantities have been measured with the same unit. If the measurements are not in the same units, we must first convert them to the same units.

We know that to simplify a fraction, we divide out common factors. Similarly in a ratio of measurements, we divide out the common unit.

Try it! – Writing Rate as a Ratio

The Americans with Disabilities Act (ADA) Guidelines for wheel chair ramps require a maximum vertical rise of 1 inch for every 1 foot of horizontal run. What is the ratio of the rise to the run?

Solution

In a ratio, the measurements must be in the same units. We can change feet to inches, or inches to feet. It is usually easier to convert to the smaller unit, since this avoids introducing more fractions into the problem.

Write the words that express the ratio.

Steps

Conversion

Ratio of the rise to the run

Write the ratio as a fraction.

$\displaystyle \frac{\text{rise}}{\text{run}}$

Substitute in the given values.

$\displaystyle \frac{1 \, \text{inch}}{1 \, \text{foot}}$

Convert 1 foot to inches.

$\displaystyle \frac{1 \, \text{inch}}{12 \, \text{inches}}$

Simplify, dividing out common factors and units.

$\displaystyle \frac{1}{12}$

So the ratio of rise to run is 1 to 12. This means that the ramp should rise 1 inch for every 12 inches of horizontal run to comply with the guidelines.

Find Unit Rates^[4]

In the last example, we calculated that Bob was driving at a rate of $\displaystyle \frac{175 \text{ miles}}{3 \text{ hours}}}$ . This tells us that every three hours, Bob will travel 175 miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate that has a denominator of 1 unit is referred to as a unit rate.

Unit Rate

A unit rate is a rate with a denominator of 1 unit.

Unit rates are very common in our lives. For example, when we say that we are driving at a speed of 68 miles per hour we mean that we travel 68 miles in 1 hour. We would write this rate as 68 miles/hour (read 68 miles per hour). The common abbreviation for this is 68 mph. Note that when no number is written before a unit, it is assumed to be 1.

So 68 miles/hour really means $\displaystyle \frac{68 \text{ miles}}{1 \text{ hour}}$ .

Two rates we often use when driving can be written in different forms, as shown:

Example

Rate

Write

Abbreviate

Read

68 miles in 1 hour

$[latex]\displaystyle \frac{68 \text{ miles}}{1 \text{ hour}}$ [/latex]

68 miles/hour

68 mph

68 miles per hour

36 miles to 1 gallon

$[latex]\displaystyle \frac{36 \text{miles}}{3 \text{1 gallon}}$ [/latex]

36 miles/gallon

36 mpg

36 miles per gallon

Another example of unit rate that you may already know about is hourly pay rate. It is usually expressed as the amount of money earned for one hour of work. For example, if you are paid $12.50 for each hour you work, you could write that your hourly (unit) pay rate is $12.50/hour (read $12.50 per hour.)

To convert a rate to a unit rate, we divide the numerator by the denominator. This gives us a denominator of 1.

Try it! – Determining a Rate

#1

Anita was paid $384 last week for working 32 hours. What is Anita’s hourly pay rate?

Solution

Steps

Conversion

Start with a rate of dollars to hours. Then divide.

$384 last week for 32 hours

Write as a rate.

$\displaystyle \frac{\$384}{32 \, \text{hours}}$

Divide the numerator by the denominator.

$\displaystyle \frac{\$12}{1 \, \text{hour}}$

Rewrite as a rate.

$12/hour

Anita’s hourly pay rate is $12 per hour.

#2

Sven drives his car 455 miles, using 14 gallons of gasoline. How many miles per gallon does his car get?

Solution

Start with a rate of miles to gallons. Then divide.

Steps

Conversion

455 miles to 14 gallons of gas

Write as a rate.

$\displaystyle \frac{455 \, \text{miles}}{ 14 \, \text{gallons}}$

Divide 455 by 14 to get the unit rate.

$\displaystyle \frac{32.5 \, \text{miles}}{1 \, \text{gallon}}$

Sven’s car gets 32.5 miles/gallon, or 32.5 mpg.

Make Unit Conversions in the U.S. System^[5]

There are two systems of measurement commonly used around the world. Most countries use the metric system. The United States uses a different system of measurement, usually called the U.S. system. We will look at the U.S. system first.

The U.S. system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cups, pints, quarts, and gallons. Both the U.S. system and the metric system measure time in seconds, minutes, or hours.

The equivalencies among the basic units of the U.S. system of measurement are listed in the table below. The table also shows, in parentheses, the common abbreviations for each measurement.

U.S System Units

Length

Volume

1 foot (ft) = 12 inches (in)

1 mile (mi) 5280 (ft)

1 yard (yd) = 3 feet (ft)

3 teaspoons (t) = 1 tablespoon (T)

16 Tablespoons (T) = 1 cup (C)

1 cup (C) = 8 fluid ounces (fl. oz)

1 pint = 2 cups (C)

1 quart (qt) = 2 pints (pt)

1 gallon (gal) = 4 quarts (qt)

Weight

Time

1 pound (lb) = 16 ounces (oz)

1 ton = 2000 pounds (lb)

1 minute (min) = 60 seconds (s)

1 hour (h) = 60 minutes (min)

1 day = 24 hours (h)

1 week (wk) = 7 days

1 year (yr) = 365 days

In many real-life applications, we need to convert between units of measurement. We will use the identity property of multiplication to do these conversions. We’ll restate the Identity Property of Multiplication here for easy reference.

For any real numbers,

$\displaystyle \text{a } \cdot 1 = \text{ a}$

$\displaystyle 1 \cdot \text{a } = \text{a }$

To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that 1 foot is equal to 12 inches, so we can write 1 as the fraction $\displaystyle \frac{1 \, \text{ft}}{12 \, \text{in}}$ . When we multiply by this fraction, we do not change the value but just change the units.

But $\displaystyle \frac{12 \, \text{in}}{1 \, \text{ft}}$ also equals 1. How do we decide whether to multiply by $\displaystyle \frac{1 \, \text{ft}}{12 \, \text{in}}$ or $\displaystyle \frac{12 \, \text{in}}{1 \, \text{ft}}$ ? We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert 60 inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.

$\displaystyle 60 \Ccancel[myred1]{\text{ in}} \cdot \frac{1 ft}{12 \Ccancel[myred1]{\text{ in}}} = 5 ft$

On the other hand, if we wanted to convert 5 feet to inches, we would choose the fraction that has feet in the denominator.

$\displaystyle 5 \Ccancel[myred1]{\text{ ft}} \cdot \frac{12 \text{ in}}{1 \Ccancel[myred1]{\text{ ft}}} = 60 \text{ in}$

We treat the unit words like factors and ‘divide out’ common units like we do common factors.

Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
Multiply.
Simplify the fraction, performing the indicated operations and removing the common units.

Try it! – Unit Conversions

Mary Anne is 66 inches tall. What is her height in feet?

Solution

Steps

Conversion

Convert 66 inches into feet.

Multiply the measurement to be converted by 1.

$\displaystyle 66 \text{ inches} \cdot 1$

Write 1 as a fraction relating the units given and the units needed.

$\displaystyle 66 \text{ inches} \cdot \frac{1 \text{ foot}}{12 \text{ inches}}$

Multiply.

$\displaystyle \frac{66\text{ inches} \cdot 1 \text{ foot}}{12 \text{ inches}}$

Simplify the fraction.

$\displaystyle \frac{66 \Ccancel[myred1]{\text{ inches}} \cdot 1 \text{ foot}}{12 \Ccancel[myred1]{\text{ inches}}}$

$\displaystyle \frac{66 \text{ feet}}{12}$

5.5 feet

Notice that the when we simplified the fraction, we first divided out the inches.

Mary Anne is 5.5 feet tall.

When we use the Identity Property of Multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator.

Try it! – Unit Conversions

Ndula, an elephant at the San Diego Safari Park, weighs almost 3.2 tons. Convert her weight to pounds.

(credit: Guldo Da Rozze, Flickr)

A photograph of an adult elephant.

Solution

We will convert 3.2 tons into pounds, using the equivalencies in the U.S. System Units table. We will use the Identity Property of Multiplication, writing 1 as the fraction 2000 pounds1 ton.

Steps

Conversion

3.2 tons

Multiply the measurement to be converted by 1.

$\displaystyle 3.2 \text{ tons} \cdot 1$

Write 1 as a fraction relating to tons and pounds.

$\displaystyle 3.2 \Ccancel[myred1]{\text{ tons}} \cdot \frac{2000 \text{ lbs}}{1 \Ccancel[myred1]{\text{ ton}}}$

Simplify.

$\displaystyle \frac{3.2 \text{ tons} \cdot 2000 \text{ lbs}}{1 \text{ ton}}$

Multiply.

6400 lbs

Ndula weighs almost 6,400 pounds.

Sometimes to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.

Try it! – Unit Conversions

#1

Juliet is going with her family to their summer home. She will be away for 9 weeks. Convert the time to minutes.

Solution

To convert weeks into minutes, we will convert weeks to days, days to hours, and then hours to minutes. To do this, we will multiply by conversion factors of 1.

Steps

Conversion

9 weeks

Write 1 as $\displaystyle \frac{7 \text{ days}}{1 \text{ week}}$ , $\displaystyle \frac{24 \text{ hours}}{1 \text{ day}}$ , $\displaystyle \frac{60 \text{ minutes}}{1 \text{ hour}}$ .

$\displaystyle \frac{9 \text{wk}}{1} \cdot \frac{7 \text{ days}}{1 \text{ wk}} \cdot \frac{24 \text{ hr}}{1 \text{ day}} \cdot \frac{60 \text{ min}}{1 \text{ hr}}$

Cancel common units.

$\displaystyle \frac{9 \Ccancel[myred1]{\text{ wk}}}{1} \cdot \frac{7 \Ccancel[myred1]{\text{ days}}}{1 \Ccancel[myred1]{\text{ wk}}} \cdot \frac{24 \Ccancel[myred1]{\text{ hr}}}{1 \Ccancel[myred1]{\text{ day}}} \cdot \frac{60 \text{ min}}{1 \Ccancel[myred1]{\text{ hr}}}$

Multiply.

$\displaystyle \frac{9\cdot 7 \cdot 24 \cdot 60 \text{ min}}{1 \cdot 1 \cdot 1 \cdot 1} = 90, 720 \text{ min}$

Juliet will be away for 90,720 minutes.

#2

How many fluid ounces are in 1 gallon of milk?

A photograph of a milk display in a grocery store. — (credit: www.bluewaikiki.com, Flickr)

Solution

Use conversion factors to get the right units: convert gallons to quarts, quarts to pints, pints to cups, and cups to fluid ounces.

Steps

Conversion

1 gallon

Multiply the measurement to be converted by 1.

$\displaystyle \frac{1 \text{ gal}}{1} \cdot \frac{4 \text{ qt}}{1 \text{ gal}} \cdot \frac{2 \text{ pt}}{1 \text{ qt}} \cdot \frac{2 \text{ C}}{1 \text{ pt}} \cdot \frac{8 \text{ fl oz}}{1 \text{ C}}$

Simplify.

$\displaystyle \frac{1 \Ccancel[myred1]{\text{ gal}}}{1} \cdot \frac{4 \Ccancel[myred1]{\text{ qt}}}{1 \Ccancel[myred1]{\text{ gal}}} \cdot \frac{2 \Ccancel[myred1]{\text{ pt}}}{1 \Ccancel[myred1]{\text{ qt}}} \cdot \frac{2 \Ccancel[myred1]{\text{ C}}}{1 \Ccancel[myred1]{\text{ pt}}} \cdot \frac{8 \text{ fl oz}}{1 \Ccancel[myred1]{\text{ C}}}$

Multiply.

$\displaystyle \frac{1 \cdot 4 \cdot 2 \cdot 2 \cdot 8 \text{ fl oz}}{1 \cdot 1 \cdot 1 \cdot 1 \cdot 1}$

Simplify.

128 fluid ounces

There are 128 fluid ounces in a gallon.

Make Unit Conversions in the Metric System^[6]

In the metric system, units are related by powers of 10. The root words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is 1000 meters; the prefix kilo- means thousand. One centimeter is $\frac{1}{100}$ of a meter, because the prefix centi- means one one-hundredth (just like one cent is $\frac{1}{100}$ of one dollar).

The equivalencies of measurements in the metric system are shown in the following table. The common abbreviations for each measurement are given in parentheses.

Metric Measurements

Length

Mass

Volume/Capacity

1 kilometer (km) = 1000 m

1 hectometer (hm) = 100 m

1 dekameter (dam) = 10 m

1 meter (m) = 1 m

1 decimeter (dm) = 0.1 m

1 centimeter (cm) = 0.01 m

1 millimeter (mm) = 0.001 m

1 kilogram (kg) = 1000 g

1 hectogram (hg) = 100 g

1 dekagram (dag) = 10 g

1 gram (g) = 1 g

1 decigram (dg) = 0.1 g

1 centigram (cg) = 0.01 g

1 milligram (mg) = 0.001 g

1 kiloliter (kL) = 1000 L

1 hectoliter (hL) = 100 L

1 dekaliter (daL) = 10 L

1 liter (L) = 1 L

1 deciliter (dL) = 0.1 L

1 centiliter (cL) = 0.01 L

1 milliliter (mL) = 0.001 L

1 meter (m) = 100 centimeters (cm)

1 meter (m) = 1000 millimeters (mm)

1 gram (g) = 100 centigrams (cg)

1 gram (g) = 1000 milligrams (mg)

1 liter (L) = 100 centiliters (cL)

1 liter (L) = 1000 milliliters (mL)

To make conversions in the metric system, we will use the same technique we did in the U.S. system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.

Have you ever run a 5 k or 10 k race? The lengths of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.

Try it! – Unit Conversions

#1

Nick ran a 10-kilometer race. How many meters did he run?

A photograph of 8 male runners in a track race. — (credit: William Warby, Flickr)

Solution

We will convert kilometers to meters using the Identity Property of Multiplication and the equivalencies in the Metric Measurements table.

Steps

Conversion

10 kilometers

Multiply the measurement to be converted by 1.

$10 \textcolor{red}{\text{ m}} \cdot 1$

Write 1 as a fraction relating to kilometers and meters.

$\displaystyle 10 \textcolor{red}{\text{ km}} \cdot \frac{1000 \text{ m}}{1 \textcolor{red}{\text{ km}}}$

Simplify.

$\displaystyle 10 \Ccancel[myred1]{\textcolor{red}{\text{ km}}} \cdot \frac{1000 \text{ m}}{1 \textcolor{red}{\Ccancel[myred1]{\text{ km}}}}$

Multiply.

$\displaystyle 10,000 \text{ m}$

Nick ran $\displaystyle 10,000$ meters.

#2

Eleanor’s newborn baby weighed 3200 grams. How many kilograms did the baby weigh?

Solution

We will convert grams to kilograms.

Steps

Conversion

$\displaystyle 3200 \textcolor{red}{\text{ grams}}$

Multiply the measurement to be converted by 1.

$\displaystyle 3200 \textcolor{red}{\text{ g}} \cdot 1$

Write 1 as a fraction relating kilograms and grams.

$\displaystyle 3200\textcolor{red}{\text{ g}} \cdot \frac{1 \text{ kg}}{1000 \textcolor{red}{\text{ g}}}$

Simplify.

$\displaystyle 3200\textcolor{red}{\Ccancel[myred1]{\text{ g}}} \cdot \frac{1 \text{ kg}}{1000 \textcolor{red}{\Ccancel[myred1]{\text{ g}}}}$

Multiply.

$\displaystyle \frac{3200 {\text{ kilograms}}}{1000}$

Divide.

3.2 kilograms

The baby weighed 3.2 kilograms.

Since the metric system is based on multiples of ten, conversions involve multiplying by multiples of ten. In Decimal Operations, we learned how to simplify these calculations by just moving the decimal.

To multiply by 10, 100, or 1000, we move the decimal to the right 1, 2, or 3 places, respectively. To multiply by 0.1, 0.01, or 0.001, we move the decimal to the left 1, 2, or 3 places, respectively.

We can apply this pattern when we make measurement conversions in the metric system.

We change 3200 grams to kilograms by multiplying by $\displaystyle \frac{1}{1000}$ (or 0.001). This is the same as moving the decimal 3 places to the left.

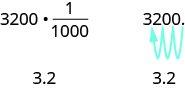Multiplying 3200 by 1 over 1000 gives 3.2. Notice that the answer, 3.2, is similar to the original value, 3200, just with the decimal moved three places to the left.

Try it! – Unit Conversions

Convert:

a. 350 liters to kiloliters

b. 4.1 liters to milliliters.

Solution

a. We will convert liters to kiloliters. The Metric Measurements table shows that 1 kiloliter = 1000 liters.

Steps

Conversion

350 L

Multiply by 1, writing 1 as a fraction relating liters to kiloliters.

$\displaystyle 350 \text{ kL} \cdot \frac{1 {\text{kL}}}{1000 \text{L}}$

Simplify.

$\displaystyle 350 \Ccancel[myred1]{\text{ kL}} \cdot \frac{1 {\text{kL}}}{1000 \Ccancel[myred1]{\text{L}}}$

Move the decimal 3 units to the left.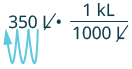

0.35 kL

b. We will convert liters to milliliters. In the Metric Measurements table, we see that 1 liter = 1000 milliliters.

Steps

Conversion

4.1 L

Multiply by 1, writing 1 as a fraction relating milliliters to liters.

$\displaystyle 4.1 \text{ L} \cdot \frac{1000 \text{ mL}}{1 \text{ L}}$

Simplify.

$\displaystyle 4.1 \Ccancel[myred1]{\text{ L}} \cdot \frac{1000 \text{ mL}}{1 \Ccancel[myred1]{\text{ L}}}$

Move the decimal 3 units to the left.

4100 mL

Convert Between U.S. and Metric Systems of Measurement^[7]

Many measurements in the United States are made in metric units. A drink may come in 2-liter bottles, calcium may come in 500-mg capsules, and we may run a 5-K race. To work easily in both systems, we need to be able to convert between the two systems.

The following table shows some of the most common conversions.

*Conversion Factors Between U.S. and Metric Systems*
Length	Weight	Volume
1 in = 2.54 cm 1 ft = 0.305 m 1 yd = 0.914 m 1 mi = 1.61 km 1 m = 3.28 ft	1 lb = 0.45 kg 1 oz = 28 g 1 kg = 2.2 lb	1 qt = 0.95 L 1 fl oz = 30 mL 1 L = 1.06 qt

We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.

Try it! – Unit Conversions

Lee’s water bottle holds 500 mL of water. How many fluid ounces are in the bottle? Round to the nearest tenth of an ounce.

Solution

Steps

Conversion

500 mL

Multiply by a unit conversion factor relating to mL and ounces.

$\displaystyle 500 \Ccancel[myred1]{\text{ mL}} \cdot \frac{1 \text{ fl oz}}{30 \Ccancel[myred1]{\text{ mL}}}$

Simplify.

$\displaystyle \frac{500 \text{ fl oz}}{30}$

Divide.

16.7 fl. oz.

The water bottle holds 16.7 fluid ounces.

The conversion factors in the Conversion Factors Between U.S. and Metric Systems table are not exact, but the approximations they give are close enough for everyday purposes. In this exercise, we rounded the number of fluid ounces to the nearest tenth.

Try it! – Unit Conversions

Soleil lives in Minnesota but often travels to Canada for work. While driving on a Canadian highway, she passes a sign that says the next rest stop is in 100 kilometers. How many miles until the next rest stop? Round your answer to the nearest mile.

Solution

Steps

Conversion

100 kilometers

Multiply by a unit conversion factor relating to kilometers and miles.

$\displaystyle 100 \Ccancel[myred1]{\text{ kilometers}} \cdot \frac{1 \text{ mile}}{1.61 \Ccancel[myred1]{\text{ kilometers}}}$

$\displaystyle 100 \cdot \frac{1 \text{ mi}}{1.61}$

Simplify.

$\displaystyle\frac{100 \text{ mi}}{1.61}$

Divide.

62 mi

It is about 62 miles to the next rest stop.

Key Concepts

Making Unit Conversions
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction, performing the indicated operations and removing the common units.
Conversions within US units

U.S. System Units

Length

Volume

1 foot (ft) = 12 inches (in)

1 mile (mi) 5280 (ft)

1 yard (yd) = 3 feet (ft)

3 teaspoons (t) = 1 tablespoon (T)

16 tablespoons (T) = 1 cup (C)

1 cup (C) = 8 fluid ounces (fl oz)

1 pint (pt) = 2 cups (C)

1 quart (qt) = 2 pints (pt)

1 gallon (gal) = 4 quarts (qt)

Weight

Time

1 pound (lb) = 16 ounces (oz)

1 ton = 2000 pounds (lb)

1 minute (min) = 60 seconds (s)

1 hour (h) = 60 minutes (min)

1 day = 24 hours (h)

1 week (wk) = 7 days

1 year (yr) = 365 days

Converting within the metric system

Metric Measurements

Length

Mass

Volume/Capacity

1 kilometer (km) = 1000 m

1 hectometer (hm) = 100 m

1 dekameter (dam) = 10 m

1 meter (m) = 1 m

1 decimeter (dm) = 0.1 m

1 centimeter (cm) = 0.01 m

1 millimeter (mm) = 0.001 m

1 kilogram (kg) = 1000 g

1 hectogram (hg) = 100 g

1 dekagram (dag) = 10 g

1 gram (g) = 1 g

1 decigram (dg) = 0.1 g

1 centigram (cg) = 0.01 g

1 milligram (mg) = 0.001 g

1 kiloliter (kL) = 1000 L

1 hectoliter (hL) = 100 L

1 dekaliter (daL) = 10 L

1 liter (L) = 1 L

1 deciliter (dL) = 0.1 L

1 centiliter (cL) = 0.01 L

1 milliliter (mL) = 0.001 L

1 meter = 100 centimeters

1 meter = 1000 millimeters

1 gram = 100 centigrams

1 gram = 1000 milligrams

1 liter = 100 centiliters

1 liter = 1000 milliliters

Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
Section material derived from Openstax Prealgebra: Decimals-Ratios and Rate ↵
Section material derived from Openstax Prealgebra: Decimals-Ratios and Rate ↵
Section material derived from Openstax Prealgebra: Decimals-Ratios and Rate ↵
Section material derived from Openstax Prealgebra: The Properties of Real Numbers-Systems of Measurement ↵
Section material derived from Openstax Prealgebra: The Properties of Real Numbers-Systems of Measurement ↵
Section material derived from Openstax Prealgebra: The Properties of Real Numbers-Systems of Measurement ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Write a Rate as a Fraction [2]

Ratios of Two Measurements in Different Units [3]

Find Unit Rates[4]

Make Unit Conversions in the U.S. System[5]

Make Unit Conversions in the Metric System[6]

Convert Between U.S. and Metric Systems of Measurement[7]

License

Share This Book

Write a Rate as a Fraction ^[2]

Ratios of Two Measurements in Different Units ^[3]

Find Unit Rates^[4]

Make Unit Conversions in the U.S. System^[5]

Make Unit Conversions in the Metric System^[6]

Convert Between U.S. and Metric Systems of Measurement^[7]