9 Fractions:
Topics Covered[1]
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
Simplifying Fractions[2]
A fraction is a way to represent parts of a whole. The fraction ![]() represents two of three equal parts. In the fraction
represents two of three equal parts. In the fraction ![]() , the 2 is called the numerator and the 3 is called the denominator. The line is called the fraction bar.
, the 2 is called the numerator and the 3 is called the denominator. The line is called the fraction bar.
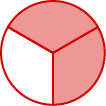 In the circle,
In the circle, ![]() of the circle is shaded, 2 of the 3 equal parts.
of the circle is shaded, 2 of the 3 equal parts.
Fraction, Numerator, and Denominator
A fraction is written ab, where b≠0 and a is the numerator and b is the denominator.
A fraction represents parts of a whole. The denominator b is the number of equal parts the whole has been divided into, and the numerator a indicates how many parts are included.
Fractions that have the same value are equivalent fractions.
The Equivalent Fractions Property allows us to find equivalent fractions and also simplify fractions.
A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator.
For example, ![]() is simplified because there are no common factors of 2 and 3.
is simplified because there are no common factors of 2 and 3. ![]() is not simplified because 5 is a common factor of 10 and 15.
is not simplified because 5 is a common factor of 10 and 15.
We simplify, or reduce, a fraction by removing the common factors of the numerator and denominator. A fraction is not simplified until all common factors have been removed. If an expression has fractions, it is not completely simplified until the fractions are simplified.
Sometimes it may not be easy to find common factors of the numerator and denominator. When this happens, a good idea is to factor the numerator and the denominator into prime numbers. Then divide out the common factors using the Equivalent Fractions Property.
How To Simplify a Fraction
Simplify: ![]()



We now summarize the steps you should follow to simplify fractions.
- Rewrite the numerator and denominator to show the common factors.
If needed, factor the numerator and denominator into prime numbers first. - Simplify using the Equivalent Fractions Property by dividing out common factors.
- Multiply any remaining factors.
Least Common Denominator[3]
In the previous section, we explained how to add and subtract fractions with a common denominator. But how can we add and subtract fractions with unlike denominators?
Let’s think about coins again. Can you add one quarter and one dime? You could say there are two coins, but that’s not very useful. To find the total value of one quarter plus one dime, you change them to the same kind of unit—cents. One quarter equals 25 cents and one dime equals 10 cents, so the sum is 35 cents. See the image below.

Similarly, when we add fractions with different denominators we have to convert them to equivalent fractions with a common denominator. With the coins, when we convert to cents, the denominator is 100. Since there are 100 cents in one dollar, 25 cents is ![]() and 10 cents is
and 10 cents is ![]() . So, we add
. So, we add ![]() to get
to get ![]() , which is 35 cents.
, which is 35 cents.
You have practiced adding and subtracting fractions with common denominators. Now let’s see what you need to do with fractions that have different denominators.
First, we will use fraction tiles to model finding the common denominator of ![]() and
and ![]() .
.
We’ll start with one ![]() tile and
tile and ![]() tile. We want to find a common fraction tile that we can use to match both
tile. We want to find a common fraction tile that we can use to match both ![]() and
and ![]() exactly.
exactly.
If we try the ![]() pieces, 2 of them exactly match the
pieces, 2 of them exactly match the ![]() pieces, but they do not exactly match the
pieces, but they do not exactly match the ![]() pieces.
pieces.

If we try the ![]() pieces, they do not exactly cover the
pieces, they do not exactly cover the ![]() pieces or the
pieces or the ![]() pieces.
pieces.

If we try the ![]() pieces, we see that exactly 3 of them cover the
pieces, we see that exactly 3 of them cover the ![]() pieces, and exactly 2 of them cover the
pieces, and exactly 2 of them cover the ![]() pieces.
pieces.
 If we were to try the
If we were to try the ![]() pieces, they would also work.
pieces, they would also work.
 Even smaller tiles, such as
Even smaller tiles, such as ![]() and
and ![]() , would also exactly cover the
, would also exactly cover the ![]() pieces and the
pieces and the ![]() pieces.
pieces.
Least Common Denominator
The denominator of the largest piece that covers both fractions is the least common denominator (LCD) of the two fractions. So, the least common denominator of ![]() and
and ![]() is 6.
is 6.
Notice that all of the tiles that cover ![]() and
and ![]() have something in common: Their denominators are common multiples of 2 and 3, the denominators of
have something in common: Their denominators are common multiples of 2 and 3, the denominators of ![]() and
and ![]() . The least common multiple (LCM) of the denominators is 6, and so we say that 6 is the least common denominator (LCD) of the fractions
. The least common multiple (LCM) of the denominators is 6, and so we say that 6 is the least common denominator (LCD) of the fractions ![]() and
and ![]() .
.
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
To find the LCD of two fractions, we will find the LCM of their denominators. We follow the procedure we used earlier to find the LCM of two numbers. We only use the denominators of the fractions, not the numerators, when finding the LCD.
Try-it! – Finding the LCD of Two Fractions
Find the LCD for the fractions ![]() and
and ![]() .
.
| Steps | Algebraic |
| Factor each denominator into its primes. | 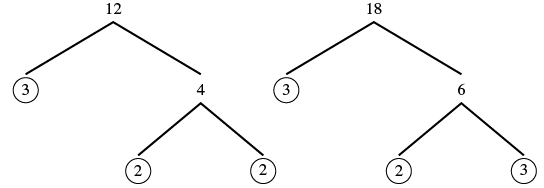 |
| List the primes of 12 and the primes of 18 lining them up in columns when possible. |  |
| Bring down the columns. |  |
| Multiply the factors. The product is the LCM. | LCM = 36 |
| The LCM of 12 and 18 is 36, so the LCD of 712 and 518 is 36. | LCD of |
To find the LCD of two fractions, find the LCM of their denominators. Notice how the steps shown below are similar to the steps we took to find the LCM.
- Factor each denominator into its primes.
- List the primes, matching primes in columns when possible.
- Bring down the columns.
- Multiply the factors. The product is the LCM of the denominators.
- The LCM of the denominators is the LCD of the fractions.
Try-it! – Finding the LCD of Two Fractions
Find the least common denominator for the fractions ![]() and
and ![]() .
.
To find the LCD, we find the LCM of the denominators.
Find the LCM of 15 and 24.
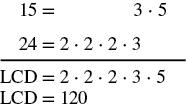
The LCM of 15 and 24 is 120. So, the LCD of ![]() and
and ![]() is 120.
is 120.
Convert to Equivalent Fractions [4]
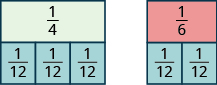
Earlier, we used fraction tiles to see that the LCD of ![]() and
and ![]() is 12. We saw that three
is 12. We saw that three ![]() pieces exactly covered
pieces exactly covered ![]() and two
and two ![]() pieces exactly covered
pieces exactly covered ![]() , so
, so
 We say that
We say that ![]() and
and ![]() are equivalent fractions and also that
are equivalent fractions and also that ![]() and
and ![]() are equivalent fractions.
are equivalent fractions.
We can use the Equivalent Fractions Property to algebraically change a fraction to an equivalent one. Remember, two fractions are equivalent if they have the same value. The Equivalent Fractions Property is repeated below for reference.
If a, b, c are whole numbers where ![]() ,
, ![]() , then
, then
![]() and
and ![]()
To add or subtract fractions with different denominators, we will first have to convert each fraction to an equivalent fraction with the LCD. Let’s see how to change ![]() and
and ![]() to equivalent fractions with denominator 12 without using models.
to equivalent fractions with denominator 12 without using models.
Try-it!
Convert ![]() and
and ![]() to equivalent fractions with denominator 12, their LCD.
to equivalent fractions with denominator 12, their LCD.
| Steps | Algebraic |
| Find the LCD. | The LCD of 14 and 16 is 12. |
| Find the number to multiply 4 to get 12. |  |
| Find the number to multiply 6 to get 12. |  |
| Use the Equivalent Fractions Property to convert each fraction to an equivalent fraction with the LCD, multiplying both the numerator and denominator of each fraction by the same number. | 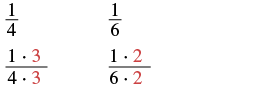 |
| Simplify the numerators and denominators. | 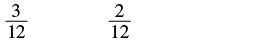 |
We do not reduce the resulting fractions. If we did, we would get back to our original fractions and lose the common denominator.
How to Convert Two Fractions to Equivalent Fractions with their LCD as the Common Denominator:
- Find the LCD.
- For each fraction, determine the number needed to multiply the denominator to get the LCD.
- Use the Equivalent Fractions Property to multiply both the numerator and denominator by the number you found in Step 2.
- Simplify the numerator and denominator.
Try-it! – Converting to Equivalent Fractions with an LCD
Convert ![]() and
and ![]() to equivalent fractions with denominator 120, their LCD.
to equivalent fractions with denominator 120, their LCD.
| Steps | Algebraic |
| The LCD is 120. We will start at Step 2. | |
| Find the number that must multiply 15 to get 120. | 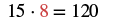 |
| Find the number that must multiply 24 to get 120. | 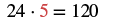 |
| Use the Equivalent Fractions Property. | 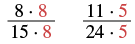 |
| Simplify the numerators and denominators. |  |
Add and Subtract Fractions[5]
How many quarters are pictured? One quarter plus 2 quarters equals 3 quarters.

Remember, quarters are really fractions of a dollar. Quarters are another way to say fourths. So the picture of the coins shows that
![]()
![]()
![]()
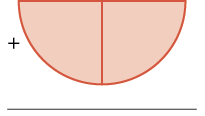
Let’s use fraction circles to model the same example, ![]() +
+ ![]() .
.
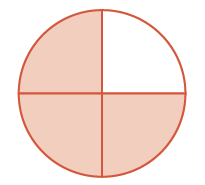
| Steps | Visual Representation | Algebraic |
| Start with one |
 |
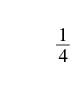 |
| Add two more |
 |
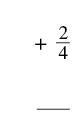 |
| The result is |
 |
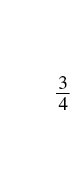 |
So again, we see that
Try-it! – Adding Fractions
| Steps | Visual Representation | Algebraic |
| Start with three |
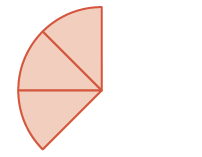 |
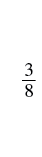 |
| Add two |
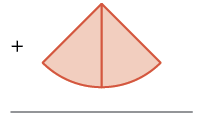 |
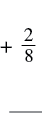 |
| How many |
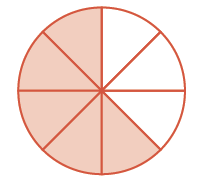 |
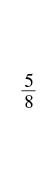 |
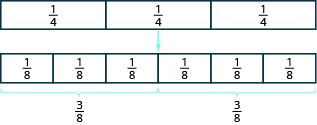
There are five ![]() pieces, or five-eighths. The model shows that
pieces, or five-eighths. The model shows that ![]() .
.
If a, b, and c are numbers where c ≠ 0, then
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
How To:
- Do they have a common denominator?
- Yes—go to step 2.
- No—rewrite each fraction with the LCD (least common denominator).
- Find the LCD.
- Change each fraction into an equivalent fraction with the LCD as its denominator.
- Add or subtract the fractions.
- Simplify, if possible.
Adding and Subtracting Fractions by Finding Factors and LCDs[6]
Once we have converted two fractions to equivalent forms with common denominators, we can add or subtract them by adding or subtracting the numerators.
How To:
- Find the LCD.
- Convert each fraction to an equivalent form with the LCD as the denominator.
- Add or subtract the fractions.
- Write the result in simplified form.
Try-it! – Adding Fractions
Add: ![]() .
.
| Steps | Algebraic |
Find the LCD of 2, 3.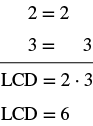 |
|
| Change into equivalent fractions with the LCD 6. | 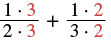 |
| Simplify the numerators and denominators. | |
| Add. |
Remember, always check to see if the answer can be simplified. Since 5 and 6 have no common factors, the fraction 56 cannot be reduced.
When we use the Equivalent Fractions Property, there is a quick way to find the number you need to multiply by to get the LCD. Write the factors of the denominators and the LCD just as you did to find the LCD. The “missing” factors of each denominator are the numbers you need. The LCD, 36, has 2 factors of 2 and 2 factors of 3.
The LCD, 36, has 2 factors of 2 and 2 factors of 3.
Twelve has two factors of 2, but only one of 3—so it is ‘missing‘ one 3. We multiplied the numerator and denominator of ![]() by 3 to get an equivalent fraction with denominator 36.
by 3 to get an equivalent fraction with denominator 36.
Eighteen is missing one factor of 2—so you multiply the numerator and denominator ![]() by 2 to get an equivalent fraction with denominator 36. We will apply this method as we subtract the fractions in the next example.
by 2 to get an equivalent fraction with denominator 36. We will apply this method as we subtract the fractions in the next example.
Try-it! – Subtracting Fractions
Subtract: ![]() .
.
| Steps | Algebraic |
Find the LCD.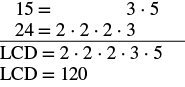 15 is ‘missing’ three factors of 2 24 is ‘missing’ a factor of 5 |
|
| Rewrite as equivalent fractions with the LCD. | 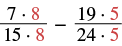 |
| Simplify each numerator and denominator. | |
| Subtract. | |
| Rewrite showing the common factor of 3. | |
| Remove the common factor to simplify. |
Try-it! – Adding with Negative Fractions
Add: ![]() .
.
| Steps | Algebraic |
Find the LCD.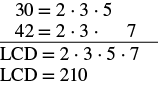 |
|
| Rewrite as equivalent fractions with the LCD. | 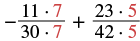 |
| Simplify each numerator and denominator. | |
| Add. | |
| Rewrite showing the common factor of 2. | |
| Remove the common factor to simplify. |
In the next example, one of the fractions has a variable in its numerator. We follow the same steps as when both numerators are numbers.
Access Additional Online Resources
Multiply fractions[7]
A model may help you understand multiplication of fractions. We will use fraction tiles to model ![]() . To multiply
. To multiply ![]() and
and ![]() , think
, think ![]() of
of ![]() .
.
Start with fraction tiles for three-fourths. To find one-half of three-fourths, we need to divide them into two equal groups. Since we cannot divide the three ![]() tiles evenly into two parts, we exchange them for smaller tiles.
tiles evenly into two parts, we exchange them for smaller tiles.
 We see
We see ![]() is equivalent to
is equivalent to ![]() . Taking half of the six
. Taking half of the six ![]() tiles gives us three
tiles gives us three ![]() tiles, which is
tiles, which is ![]() .
.
Therefore,
Try-it! – Multiplying Fractions
Use a diagram to model ![]() .
.
First shade in ![]() of the rectangle.
of the rectangle.
 We will take
We will take ![]() of this
of this ![]() , so we heavily shade
, so we heavily shade ![]() of the shaded region.
of the shaded region.
 Notice that 3 out of the 8 pieces are heavily shaded. This means that
Notice that 3 out of the 8 pieces are heavily shaded. This means that ![]() of the rectangle is heavily shaded.
of the rectangle is heavily shaded.
Therefore, ![]() of
of ![]() is
is ![]() , or
, or ![]() .
.
Look at the result we got above. We found that ![]() . Do you notice that we could have gotten the same answer by multiplying the numerators and multiplying the denominators?
. Do you notice that we could have gotten the same answer by multiplying the numerators and multiplying the denominators?
| Steps | Algebraic |
| Multiply the numerators and multiply the denominators. | |
| Simplify. |
This leads to the definition of fraction multiplication. To multiply fractions, we multiply the numerators and multiply the denominators. Then we write the fraction in simplified form.
If a, b, c, and d are numbers where ![]() and
and ![]() , then
, then
Try-it! – Multiplying Fractions
Multiply, and write the answer in simplified form: ![]() .
.
| Steps | Algebraic |
| Multiply the numerators; multiply the denominators. | |
| Simplify. |
There are no common factors, so the fraction is simplified.
When multiplying fractions, the properties of positive and negative numbers still apply. It is a good idea to determine the sign of the product as the first step. In Example 4.26 we will multiply two negatives, so the product will be positive.
Try-it! – Multiplying Fractions with Negatives
Multiply, and write the answer in simplified form: ![]() .
.
| Steps | Algebraic |
| The signs are the same, so the product is positive. Multiply the numerators, multiply the denominators. | |
| Simplify. | |
| Look for common factors in the numerator and denominator. Rewrite showing common factors. | 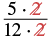 |
| Remove common factors. |
Another way to find this product involves removing common factors earlier.
| Steps | Algebraic |
| Determine the sign of the product. Multiply. | |
| Show common factors and then remove them. | 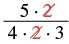 |
| Multiply remaining factors. |
We get the same result.
Try-it! – Multiplying Fractions with Negatives
Multiply, and write the answer in simplified form: ![]() .
.
| Steps | Algebraic |
| Determine the sign of the product; multiply. | |
| Are there any common factors in the numerator and the denominator? We know that 7 is a factor of 14 and 21, and 5 is a factor of 20 and 15. |
|
| Rewrite showing common factors. | 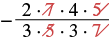 |
| Remove the common factors. | |
| Multiply the remaining factors. |
When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, a, can be written as a1. So, ![]() , for example.
, for example.
Try-it! – Multiplying Fractions, Whole Numbers, and Terms
Multiply, and write the answer in simplified form:
a. ![]()
b. ![]()
| Steps | Algebraic |
| Write 56 as a fraction. | |
| Determine the sign of the product; multiply. | |
| Simplify. | 8 |
b.
| Steps | Algebraic |
| Write −20x as a fraction. | |
| Determine the sign of the product; multiply. | |
| Show common factors and then remove them. | 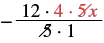 |
| Multiply remaining factors; simplify. | −48x |
Find Reciprocals[8]
The fractions ![]() and
and ![]() are related to each other in a special way. So are
are related to each other in a special way. So are ![]() and
and ![]() . Do you see how? Besides looking like upside-down versions of one another, if we were to multiply these pairs of fractions, the product would be 1.
. Do you see how? Besides looking like upside-down versions of one another, if we were to multiply these pairs of fractions, the product would be 1.
Such pairs of numbers are called reciprocals.
Reciprocal
- The reciprocal of the fraction
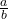 is
is 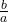 where a≠0 and b≠0.
where a≠0 and b≠0.
A number and its reciprocal have a product of 1.
- To find the reciprocal of a fraction, we invert the fraction. This means that we place the numerator in the denominator and the denominator in the numerator.
To get a positive result when multiplying two numbers, the numbers must have the same sign. So, reciprocals must have the same sign.
 To find the reciprocal, keep the same sign and invert the fraction. The number zero does not have a reciprocal. Why? A number and its reciprocal multiply to 1. Is there any number r so that 0 · r = 1? No. So, the number 0 does not have a reciprocal.
To find the reciprocal, keep the same sign and invert the fraction. The number zero does not have a reciprocal. Why? A number and its reciprocal multiply to 1. Is there any number r so that 0 · r = 1? No. So, the number 0 does not have a reciprocal.
Try-it! – Finding Reciprocals
Find the reciprocal of each number. Then check that the product of each number and its reciprocal is 1.
a. ![]()
b. ![]()
c. ![]()
d. 7
To find the reciprocals, we keep the sign and invert the fractions.
a.
| Steps | Algebraic |
| Find the reciprocal of |
The reciprocal of |
| Check: | |
| Multiply the number and its reciprocal. | |
| Multiply numerators and denominators. | |
| Simplify. | 1 ✓ |
b.
| Steps | Algebraic |
| Find the reciprocal of |
|
| Simplify. | -6 |
| Check: | |
| 1 ✓ |
c.
| Steps | Algebraic |
| Find the reciprocal of |
|
| Check: | |
| 1 ✓ |
d.
| Steps | Algebraic |
| Find the reciprocal of 7. | |
| Write 7 as a fraction. | |
| Write the reciprocal of 71. | |
| Check: | |
| 1 ✓ |
In a previous chapter, we worked with opposites and absolute values. The table below compares opposites, absolute values, and reciprocals.
| Opposite | Absolute Value | Reciprocal |
|---|---|---|
| has opposite sign | is never negative | has same sign, fraction inverts |
Try-it! – Reciprocals and Opposites
Fill in the chart for each fraction in the left column:
| Number | Opposite | Absolute Value | Reciprocal |
|---|---|---|---|
| -5 |
To find the opposite, change the sign. To find the absolute value, leave the positive numbers the same, but take the opposite of the negative numbers. To find the reciprocal, keep the sign the same and invert the fraction.
| Number | Opposite | Absolute Value | Reciprocal |
|---|---|---|---|
| 2 | |||
| -5 | 5 | 5 |
Divide Fractions[9]
Why is 12 ÷ 3 = 4? We previously modeled this with counters. How many groups of 3 counters can be made from a group of 12 counters?
 There are 4 groups of 3 counters. In other words, there are four 3s in 12. So, 12 ÷ 3 = 4.
There are 4 groups of 3 counters. In other words, there are four 3s in 12. So, 12 ÷ 3 = 4.
What about dividing fractions? Suppose we want to find the quotient: ![]() . We need to figure out how many
. We need to figure out how many ![]() s there are in
s there are in ![]() . We can use fraction tiles to model this division. We start by lining up the half and sixth fraction tiles as shown below. Notice, there are three
. We can use fraction tiles to model this division. We start by lining up the half and sixth fraction tiles as shown below. Notice, there are three ![]() tiles in
tiles in ![]() , so
, so ![]()

Try-it! – Dividing Fractions
Model: ![]() .
.
Solution
We want to determine how many ![]() s are in
s are in ![]() . Start with one
. Start with one ![]() tile. Line up
tile. Line up ![]() tiles underneath the
tiles underneath the ![]() tile.
tile. There are two
There are two ![]() s in
s in ![]() .
.
So, ![]() .
.
We are trying to determine how many ![]() s there are in 2. We can model this as shown.
s there are in 2. We can model this as shown. Because there are eight
Because there are eight ![]() s in 2,
s in 2, ![]() .
.
Let’s use money to model ![]() in another way. We often read
in another way. We often read ![]() as a ‘quarter’, and we know that a quarter is one-fourth of a dollar. So, we can think of
as a ‘quarter’, and we know that a quarter is one-fourth of a dollar. So, we can think of ![]() as, “How many quarters are there in two dollars?” One dollar is 4 quarters, so 2 dollars would be 8 quarters. So again,
as, “How many quarters are there in two dollars?” One dollar is 4 quarters, so 2 dollars would be 8 quarters. So again, ![]() .
.

The U.S. coin called a quarter is worth one-fourth of a dollar.
Using fraction tiles, we showed that ![]() . Notice that
. Notice that ![]() also. How are
also. How are ![]() and
and ![]() related? They are reciprocals. This leads us to the procedure for fraction division.
related? They are reciprocals. This leads us to the procedure for fraction division.
If a, b, c, and d are numbers where ![]() ,
, ![]() ,and
,and ![]() , then
, then
We need to say b ≠ 0, c ≠ 0 and d ≠ 0 to be sure we don’t divide by zero.
Try-it! – Dividing Fractions
Divide and write the answer in simplified form: ![]()
Solution
| Steps | Algebraic |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. The product is negative. |
| Steps | Algebraic |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. |
Solution
| Steps | Algebraic |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. Remember to determine the sign first. | |
| Rewrite to show common factors. | |
| Remove common factors and simplify. |
| Steps | Algebraic |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Rewrite showing common factors. | 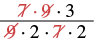 |
| Remove common factors. | |
| Simplify. |
Access Additional Online Resources
Summary of Fraction Operations[10]
Fraction multiplication: Multiply the numerators and multiply the denominators.
Fraction division: Multiply the first fraction by the reciprocal of the second.
Fraction addition: Add the numerators and place the sum over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
Convert Fractions to Decimals[11]
Remember that the fraction bar indicates division. So ![]() can be written as
can be written as ![]() or
or ![]() . This means that we can convert a fraction to a decimal by treating it as a division problem.
. This means that we can convert a fraction to a decimal by treating it as a division problem.
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
Try it! – Convert a Fraction to a Decimal
Write the fraction ![]() as a decimal.
as a decimal.
Solution
| Steps | Algebraic |
| A fraction bar means division, so we can write the fraction |
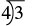 |
| Divide. | 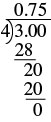 |
| So, the fraction |
Key Concepts
- Simplify a fraction.
- Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers.
- Simplify, using the equivalent fractions property, by removing common factors.
- Multiply any remaining factors.
- Fraction Addition
- If a, b, and c are numbers where c ≠ 0, then
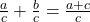 .
. - To add fractions, add the numerators and place the sum over the common denominator.
- If a, b, and c are numbers where c ≠ 0, then
- Fraction Subtraction
- If a, b, and c are numbers where c ≠ 0, then
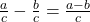 .
. - To subtract fractions, subtract the numerators and place the difference over the common denominator.
- If a, b, and c are numbers where c ≠ 0, then
- Find the least common denominator (LCD) of two fractions.
- Factor each denominator into its primes.
- List the primes, matching primes in columns when possible.
- Bring down the columns.
- Multiply the factors. The product is the LCM of the denominators.
- The LCM of the denominators is the LCD of the fractions.
- Equivalent Fractions Property
- If a, b, and c are whole numbers where b ≠ 0, c ≠ 0 then
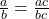 and
and 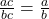
- If a, b, and c are whole numbers where b ≠ 0, c ≠ 0 then
- Convert two fractions to equivalent fractions with their LCD as the common denominator.
- Find the LCD.
- For each fraction, determine the number needed to multiply the denominator to get the LCD.
- Use the Equivalent Fractions Property to multiply the numerator and denominator by the number from Step 2.
- Simplify the numerator and denominator.
- Add or subtract fractions with different denominators.
- Find the LCD.
- Convert each fraction to an equivalent form with the LCD as the denominator.
- Add or subtract the fractions.
- Write the result in simplified form.
- Summary of Fraction Operations
- Fraction multiplication: Multiply the numerators and multiply the denominators.
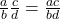
- Fraction division: Multiply the first fraction by the reciprocal of the second.
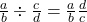
- Fraction addition: Add the numerators and place the sum over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
- Fraction multiplication: Multiply the numerators and multiply the denominators.
![]()
-
- Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
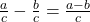
- Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
- Simplify complex fractions.
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator.
- Simplify if possible.
- Reciprocal
- A number and its reciprocal have a product of 1.
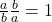
Opposite Absolute Value Reciprocal has opposite sign is never negative has same sign, fraction inverts
- A number and its reciprocal have a product of 1.
- Convert a Fraction to a Decimal: to convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
- Add mixed numbers with a common denominator.
- Add the whole numbers.
- Add the fractions.
- Simplify, if possible.
- Subtract mixed numbers with common denominators.
- Rewrite the problem in vertical form.
- Compare the two fractions.
If the top fraction is larger than the bottom fraction, go to Step 3.
If not, in the top mixed number, take one whole and add it to the fraction part, making a mixed number with an improper fraction. - Subtract the fractions.
- Subtract the whole numbers.
- Simplify, if possible.
- Subtract mixed numbers with common denominators as improper fractions.
- Rewrite the mixed numbers as improper fractions.
- Subtract the numerators.
- Write the answer as a mixed number, simplifying the fraction part, if possible
- Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
- Section material derived from Openstax Prealgebra: Fractions-Multiply and Divide Fractions ↵
- Section material derived from Openstax Prealgebra: Fractions-Add and Subtract Fractions with Different Denominators ↵
- Section material derived from Openstax Prealgebra: Fractions-Add and Subtract Fractions with Different Denominators ↵
- Section material derived from Openstax Prealgebra: Fractions-Add and Subtract Fractions with Common Denominators ↵
- Section material derived from Openstax Prealgebra: Fractions-Add and Subtract Fractions with Different Denominators ↵
- Section material derived from Openstax Prealgebra: Fractions-Multiply and Divide Fractions ↵
- Section material derived from Openstax Prealgebra: Fractions-Multiply and Divide Fractions ↵
- Section material derived from Openstax Prealgebra: Fractions-Multiply and Divide Fractions ↵
- Section material derived from Openstx Prealgebra: Fractions-Add and Subtract Fractions with Different Denominators ↵
- Section material derived from Openstax Prealgebra: Decimals-Decimals and Fractions ↵
A fraction represents parts of a whole.
Indicates how many parts are included.
Is the number of equal parts the whole has been divided into.
A fraction is considered simplified if there are no common factors in the numerator and denominator.
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
The reciprocal of the fraction [latex]\frac{a}{b}[/latex] is [latex]\frac{b}{a}[/latex] where a≠0 and b≠0.
A mixed number consists of a whole number a and a fraction bc where c≠0. It is written as abc, where c≠0.
The fraction [latex]\frac{a}{b} [/latex] is proper if a b.

