22 Exponential Growth:
Topics Covered
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
Identifying Exponential Functions[1]
India is the second most populous country in the world with a population of about 1.39 billion people in 2021. The population is growing at a rate of about 1.2% each year [2] If this rate continues, the population of India will exceed China’s population by the year 2027. When populations grow rapidly, we often say that the growth is “exponential,” meaning that something is growing very rapidly. To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.
When exploring linear equations, we observed a constant rate of change—a constant number by which the output increased for each unit increase in input. For example, in the equation ![]() , the slope tells us the output increases by 3 each time the input increases by 1. The scenario in the India population example is different because we have a percent change per unit of time (rather than a constant change) in the number of people.
, the slope tells us the output increases by 3 each time the input increases by 1. The scenario in the India population example is different because we have a percent change per unit of time (rather than a constant change) in the number of people.
What exactly does it mean to grow exponentially? What does the word double have in common with the percent increase?
- Percent change refers to a change based on a percent of the original amount.
- Exponential growth refers to an increase based on a constant multiplicative rate of change over equal increments of time, that is, a percent increase of the original amount over time.
- Exponential decay refers to a decrease based on a constant multiplicative rate of change over equal increments of time, that is, a percent decrease of the original amount over time.
For us to gain a clear understanding of exponential growth, let us contrast exponential growth with linear growth. We will construct two functions. The first function is exponential. We will start with an input of 0, and increase each input by 1. We will double the corresponding consecutive outputs. The second function is linear. We will start with an input of 0, and increase each input by 1. We will add 2 to the corresponding consecutive outputs. See the table below
| 0 | 1 | 0 |
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 8 | 6 |
| 4 | 16 | 8 |
| 5 | 10 | 32 |
| 6 | 64 | 12 |
From the table we can infer that for these two functions, exponential growth dwarfs linear growth.
- Exponential growth refers to the original value from the range increasing by the same percentage over equal increments found in the domain.
- Linear growth refers to the original value from the range increasing by the same amount over equal increments found in the domain.
Apparently, the difference between “the same percentage” and “the same amount” is quite significant. For exponential growth, over equal increments, the constant multiplicative rate of change resulted in doubling the output whenever the input increased by one. For linear growth, the constant additive rate of change over equal increments resulted in adding 2 to the output whenever the input was increased by one.
While we explore more about the growth and decay in the next section, we will first look at the equation for exponential functions. The general form of the exponential function is ![]() , where a is any nonzero number, b is a positive real number not equal to 1.
, where a is any nonzero number, b is a positive real number not equal to 1.
For any real number ![]() , an exponential function is a function with the form:
, an exponential function is a function with the form:
![]()
where,
- a is a non-zero real number called the initial value
- b is any positive real number (b >0), such that b ≠ 1
- Note you may also see the function as
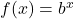 , and where b >0 and b ≠ 1.
, and where b >0 and b ≠ 1.
Notice that in this function, the variable is the exponent. In our functions so far, the variables were the base.

Our definition says ![]() . Why is that so? Well, if we let
. Why is that so? Well, if we let ![]() , then
, then ![]() becomes
becomes ![]() . Since
. Since ![]() for all real numbers,
for all real numbers, ![]() . This is the constant function.
. This is the constant function.
Our definition also says ![]() (meaning it cannot be a negative number). If we let the base be negative, say -4, then
(meaning it cannot be a negative number). If we let the base be negative, say -4, then ![]() is not a real number when
is not a real number when ![]() .
.
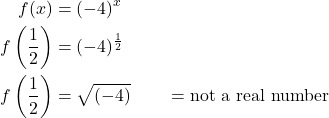
In fact, ![]() would not be a real number any time
would not be a real number any time ![]() is a fraction with an even denominator. So our definition requires
is a fraction with an even denominator. So our definition requires ![]() .
.
Try it! – Identifying Exponential Functions
Which of the following equations are not exponential functions?
Solution
By definition, an exponential function has a constant as a base and an independent variable as an exponent. Thus, ![]() does not represent an exponential function because the base is an independent variable. In fact,
does not represent an exponential function because the base is an independent variable. In fact, ![]() is a power function.
is a power function.
Recall that the base ![]() of an exponential function is always a positive constant, and
of an exponential function is always a positive constant, and ![]() . Thus,
. Thus, ![]() does not represent an exponential function because the base, −2, is less than 0.
does not represent an exponential function because the base, −2, is less than 0.
Exponential Growth and Decay [3]
The term “exponential growth” is often used in everyday language to describe anything that grows or increases rapidly. However, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.
Exponential growth grows by a rate proportional to the amount present.
The exponential functions grow faster the larger the input value is. This means that the larger the amount, the faster it will grow. AND not only will the amount itself grow larger, but the rate at which it grows will also increase.
For any real number x and any positive real numbers a and b such that b ≠ 1, an exponential growth function has the form ![]() where
where
- a is the initial or starting value of the function.
- b is the growth factor or growth multiplier per unit x . Also called the base.
In more general terms, we have an exponential function, in which a constant base is raised to a variable exponent. To differentiate between linear and exponential functions in a more practical example, let’s consider two companies, A and B. Company A has 100 stores and expands by opening 50 new stores a year, so its growth can be represented by the function ![]() . Company B has 100 stores and expands by increasing the number of stores by 50% each year, so its growth can be represented by the function
. Company B has 100 stores and expands by increasing the number of stores by 50% each year, so its growth can be represented by the function ![]() . Notice the distinction we mentioned earlier. Company A changes by the same amount per year (50 stores opened each year), while Company B exhibits a percent increase each year (# of stores increases by 50% per year). So again we are seeing a percentage change rather than a constant change. A few years of growth for these companies are illustrated below:
. Notice the distinction we mentioned earlier. Company A changes by the same amount per year (50 stores opened each year), while Company B exhibits a percent increase each year (# of stores increases by 50% per year). So again we are seeing a percentage change rather than a constant change. A few years of growth for these companies are illustrated below:
| Year, x | Stores, Company A | Stores, Company B |
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| x |
We can see in the graphs that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
Notice that the domain (all of the x-values) for both functions is ![]() , and the range (all of the y-values) for both functions is
, and the range (all of the y-values) for both functions is ![]() . After year 1, Company B always has more stores than Company A.
. After year 1, Company B always has more stores than Company A.
Now we will turn our attention to the function representing the number of stores for Company B, ![]() . In this exponential function, 100 represents the initial number of stores, 0.50 represents the growth rate, and
. In this exponential function, 100 represents the initial number of stores, 0.50 represents the growth rate, and ![]() represents the growth factor. Generalizing further, we can write this function as
represents the growth factor. Generalizing further, we can write this function as ![]() , where 100 is the initial value, 1.5 is called the base, and x is called the exponent.
, where 100 is the initial value, 1.5 is called the base, and x is called the exponent.
A note of caution if you are working with growth rate vs growth factor. In this example it specifies the expansion increases by (a rate of) 50% annually, this is growth rate (r). To determine the growth factor (our b value), use (1 + r) if the amount is increasing and if it is decreasing the decay factor (still our b value) use (1 – r). In the example, the growth factor (b in our equation) is 1+0.5. Also keep in mind that r is often given as a percentage, which should always be converted to decimal form before it is plugged into the equation.
Try it! – Evaluating a Real-World Exponential Model
At the beginning of this section, we learned that the population of India was about 1.25 billion in the year 2013, with an annual growth rate of about 1.2%. This situation is represented by the growth function ![]() , where t is the number of years since 2013. To the nearest thousandth, what will the population of India be in 2031?
, where t is the number of years since 2013. To the nearest thousandth, what will the population of India be in 2031?
Solution
To estimate the population in 2031, we evaluate the models for t=18, because 2031 is 18 years after 2013. Rounding to the nearest thousandth,
![]()
There will be about 1.549 billion people in India in the year 2031.
Try it! Writing an Exponential Model When the Initial Value Is Known
In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population had grown to 180 deer. The population was growing exponentially. Write an exponential function ![]() representing the population (N) of deer over time t.
representing the population (N) of deer over time t.
Solution
We let our independent variable t be the number of years after 2006. Thus, the information given in the problem can be written as input-output pairs: (0, 80) and (6, 180). Notice that by choosing our input variable to be measured as years after 2006, we have given ourselves the initial value for the function, ![]() . We can now substitute the second point into the equation
. We can now substitute the second point into the equation ![]() to find b:
to find b:
| Steps | Algebraic |
|---|---|
| Substitute using point (6, 180). | |
| Divide and write in lowest terms. | |
| Isolate busing properties of exponents. | |
| Round to 4 decimal places. |
NOTE: Unless otherwise stated, do not round any intermediate calculations. Then round the final answer to four places for the remainder of this section.
The exponential model for the population of deer is ![]() . (Note that this exponential function models short-term growth. As the inputs gets large, the output will get increasingly larger, so much so that the model may not be useful in the long term.)
. (Note that this exponential function models short-term growth. As the inputs gets large, the output will get increasingly larger, so much so that the model may not be useful in the long term.)
We can graph our model to observe the population growth of deer in the refuge over time. Notice that the graph in the image below passes through the initial points given in the problem, (0,80) and (6,180). We can also see that the domain for the function is ![]() , and the range for the function is
, and the range for the function is ![]() .
.
In these examples our function has been dealing with an increase or growth. But what if it is the opposite, decreasing, or what is called decay. Let’s try an example similar to the population example above, just with a decreasing population.
Try it!
In 2006, 200 deer were introduced into a wildlife refuge. By 2012, the population had dropped to 125 deer. The population was decreasing exponentially. Write an exponential function ![]() representing the population
representing the population ![]() of deer over time t.
of deer over time t.
Solution
To estimate the population in 2031, we evaluate the models for t = 6 , because 2012 is 6 years after 2006. Our a value is the initial population in 2006, 200 deer.
![]()
![]()
The exponential model for the population of deer is ![]() .
.
In the exponential function modeling growth of the form ![]() we can also use the following rules to help identify if something is growth, decay, or neither
we can also use the following rules to help identify if something is growth, decay, or neither
- If b > 1, it is growth
- If 0 < b > 1, it is decay
Try it!
#1
We have the equation ![]() the base (growth factor) is 1.25. Following our rules, we want to identify if b is greater than 1 or is between 0 and 1.
the base (growth factor) is 1.25. Following our rules, we want to identify if b is greater than 1 or is between 0 and 1.
Solution
As 1.25 is greater than 1, it would represent growth.
#2
We have the equation ![]() . what is our b value? Is it growing or decaying?
. what is our b value? Is it growing or decaying?
Solution
b is 0.58. As this is between 0 and 1, it would be decreasing or decay.
#3
For the following exercises, determine whether the equation represents exponential growth, exponential decay, or neither. Explain.
a. ![]()
b. ![]()
c. ![]()
d. ![]()
Solution
a. exponential growth; The growth factor, 1.06, is greater than 1.
b. exponential decay; The decay factor, 0.97, is between 0 and 1.
c. exponential decay; The decay factor, 0.825, is between 0 and 1.
d. neither. The base value b is negative, meaning that it is not exponential.
Graphs of Exponential Functions[4]
Now that we have defined exponential functions and growth/decay applications of exponential functions, by graphing a few exponential functions, we will be able to see their unique properties. Let’s start by looking at the function from earlier f(x) = 2x, and create a table for the outputs over the interval fro -3 to 3.
| -3 | |
| -2 | |
| -1 | |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
We can examine the graph of ![]() by plotting the ordered pairs we observe on the table above, and then make a few observations.
by plotting the ordered pairs we observe on the table above, and then make a few observations.
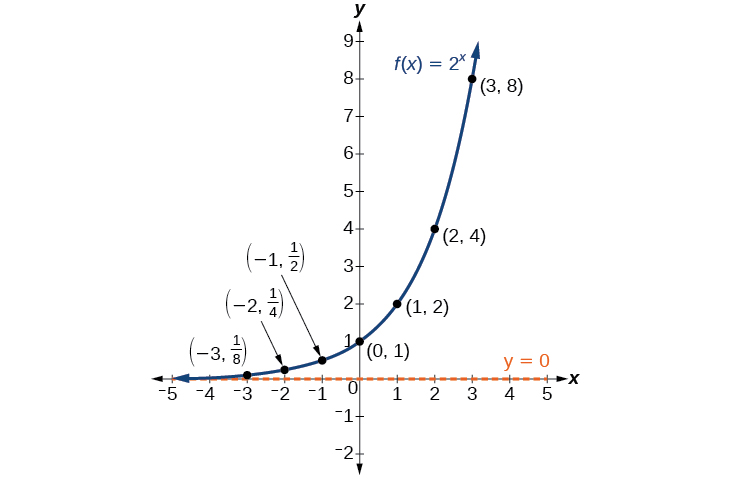
Let’s define the behavior of the graph of the exponential function ![]() and highlight some of its key characteristics.
and highlight some of its key characteristics.
- the domain is
 ,
, - the range is
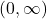 ,
, - as
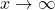 ,
, 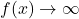 ,
, - as
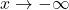 ,
, 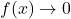 ,
, -
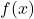 is always increasing,
is always increasing, - The graph of
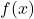 will never touch the
will never touch the 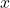 -axis because base two raised to any exponent never has the result of zero.
-axis because base two raised to any exponent never has the result of zero. -
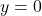 is the horizontal asymptote.
is the horizontal asymptote. - the
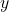 -intercept is 1.
-intercept is 1.
To summarize the features of exponential graphs:
For any real number ![]() , an exponential function is a function with the form:
, an exponential function is a function with the form:
![]()
where,
-
 is a non-zero real number called the initial value
is a non-zero real number called the initial value -
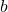 is any positive real number such that
is any positive real number such that 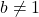 .
. - The domain of
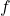 is all real numbers.
is all real numbers. - The range of
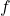 is all positive real numbers if
is all positive real numbers if 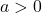 .
. - The range of
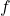 is all negative real numbers if
is all negative real numbers if 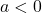 .
. - The
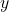 -intercept is
-intercept is 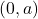 , and the horizontal asymptote is
, and the horizontal asymptote is 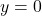 .
.
Try it! – Graphing Exponential Functions
On the same coordinate system graph ![]() and
and ![]() .
.
Solution
We will use point plotting to graph the functions.
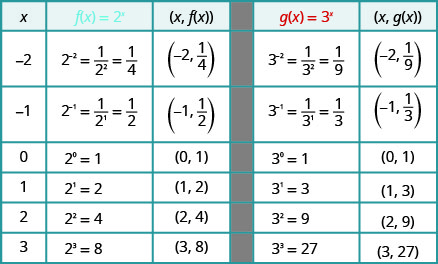
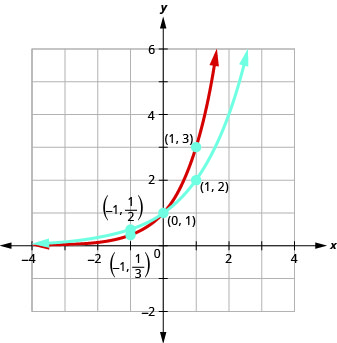
If we look at the graphs from the previous example, we can identify some of the properties of exponential functions. The graphs of ![]() and
and ![]() have the same basic shape. This is the shape we expect from an exponential function where
have the same basic shape. This is the shape we expect from an exponential function where ![]() .
.
We notice, that for each function, the graph contains the point ![]() . This makes sense because
. This makes sense because ![]() for any
for any ![]() .
.
The graph of each function, ![]() also contains the point
also contains the point ![]() . The graph of
. The graph of ![]() contained
contained ![]() and the graph of
and the graph of ![]() contained
contained ![]() . This makes sense as
. This makes sense as ![]() .
.
Notice too, the graph of each function ![]() also contains the point
also contains the point ![]() . The graph of
. The graph of ![]() contained
contained ![]() and the graph of
and the graph of ![]() contained
contained ![]() . This makes sense as
. This makes sense as ![]() .
.
What is the domain for each function? From the graphs, we can see that the domain is the set of all real numbers. There is no restriction on the domain. We write the domain in interval notation as ![]() .
.
Look at each graph. What is the range of the function? The graph never hits the ![]() -axis. The range is all positive numbers. We write the range in interval notation as
-axis. The range is all positive numbers. We write the range in interval notation as ![]() .
.
Whenever a graph of a function approaches a line but never touches it, we call that line an asymptote. For the exponential functions we are looking at, the graph approaches the ![]() -axis very closely but will never cross it, we call the line
-axis very closely but will never cross it, we call the line ![]() , the
, the ![]() -axis, a horizontal asymptote.
-axis, a horizontal asymptote.
| Property | Characteristics |
| Domain | |
| Range | |
| x-intercept | None |
| y-intercept | |
| Contains | |
| Asymptote |
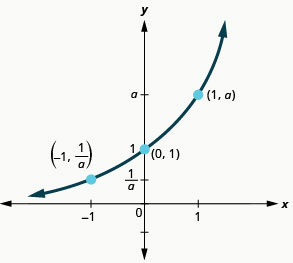
Our definition of an exponential function ![]() says
says ![]() , but the examples and discussion so far have been about functions where
, but the examples and discussion so far have been about functions where ![]() . What happens when
. What happens when ![]() ? The next example will explore this possibility.
? The next example will explore this possibility.
Try it! – Graphing Exponential Functions
On the same coordinate system, graph ![]() and
and ![]()
Solution
We will use point plotting to graph the functions.
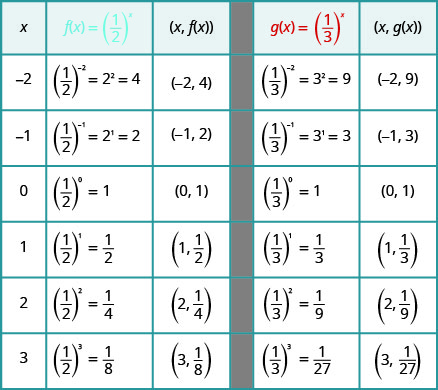
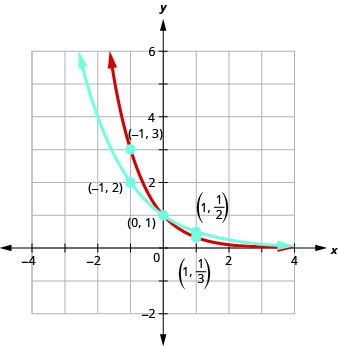
Now let’s look at the graphs from the previous Example so we can now identify some of the properties of exponential functions where ![]() .
.
The graphs of ![]() and
and ![]() have the same basic shape. While this is the shape we expect from an exponential function where
have the same basic shape. While this is the shape we expect from an exponential function where ![]() , the graphs go down from left to right while the previous graphs, when
, the graphs go down from left to right while the previous graphs, when ![]() , went from up from left to right.
, went from up from left to right.
We notice that for each function, the graph still contains the point ![]() . This makes sense because
. This makes sense because ![]() for any
for any ![]() .
.
As before, the graph of each function, ![]() , also contains the point
, also contains the point ![]() .The graph of
.The graph of ![]() contained
contained ![]() and the graph of
and the graph of ![]() contained
contained ![]() . This makes sense as
. This makes sense as ![]() .
.
Notice too that the graph of each function, ![]() , also contains the point
, also contains the point ![]() . The graph of
. The graph of ![]() contained (1,2) and the graph of
contained (1,2) and the graph of ![]() contained (1,3). This makes sense as
contained (1,3). This makes sense as ![]() .
.
What is the domain and range for each function? From the graphs, we can see that the domain is the set of all real numbers and we write the domain in interval notation as ![]() Again, the graph never hits the
Again, the graph never hits the ![]() -axis. The range is all positive numbers. We write the range in interval notation as
-axis. The range is all positive numbers. We write the range in interval notation as ![]() .
.
We will summarize these properties in the chart below. Which also includes when ![]() .
.
| when |
when |
||
|---|---|---|---|
| Domain | Domain | ||
| Range | Range | ||
| x-intercept | none | x-intercept | none |
| y-intercept | y-intercept | ||
| Contains | Contains | ||
| Asymptote | Asymptote | ||
| Basic shape | increasing | Basic shape | decreasing |
Key Concepts
- Properties of the Graph of
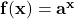 :
:
| when |
when |
||
|---|---|---|---|
| Domain | Domain | ||
| Range | Range | ||
| x-intercept | none | x-intercept | none |
| y-intercept | y-intercept | ||
| Contains | Contains | ||
| Asymptote | Asymptote | ||
| Basic shape | increasing | Basic shape | decreasing |
- The average rate of growth in a population:
- To determine if a rate of growth is exponential
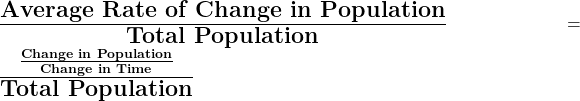
- Section material derived from Openstax College Algebra: Exponential and Logarithmic Functions-Exponential Functions and Intermediate Algebra: Exponential and Logarithmic Functions-Evaluate and Graph Exponential Functions; Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ;Access for free at https://openstax.org/books/college-algebra-corequisite-support-2e/pages/1-introduction-to-prerequisites ↵
- http://www.worldometers.info/world-population/. Accessed February 24, 2014. ↵
- Section material derived from Openstax College Algebra: Exponential and Logarithmic Functions-Exponential Functions ↵
- Section material derived from Openstax Intermediate Algebra: Exponential and Logarithmic Functions-Evaluate and Graph Exponential Functions and Precalculus: Exponential and Logarithmic Functions-Graphs of Exponential Functions; Access for free at https://openstax.org/books/precalculus-2e/pages/1-introduction-to-functions ↵
A rate of growth that increases in proportion to the original population
the set of all the x-values in the ordered pairs in the function.
the set of all the y-values in the ordered pairs in the function. To find the range we look at the graph and find all the values of y that have a corresponding value on the graph.
A line which a graph of a function approaches closely but never touches

