Simple & Compound Interest

Elizabeth Pople

17 Simple & Compound Interest

Topics Covered^[1]

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

Simple Interest
Compound Interest
Key Concepts

Simple Interest^[2]

If you deposit money into a bank account, you are effectively lending money to the bank – and you can expect to receive interest in return. Similarly, if you borrow money from a bank (or from a department store, or a car dealership, for example) then you can expect to have to pay interest on the loan. That is the price of borrowing money.

If it stayed in your wallet, you could spend it any time you wanted. If the bank looked after it for you, then they could spend it, with the plan of making a profit from it. The bank usually “pays” you to deposit it into an account, as a way of encouraging you to bank it with them, This payment is like a reward, which provides you with a reason to leave it with the bank for a while, rather than keeping the money in your wallet.

The money you put in the bank is called the principal, P, and the bank pays you interest, I. The interest is computed as a certain percent of the principal; called the rate of interest, r. The rate of interest is usually expressed as a percent per year and is calculated by using the decimal equivalent of the percent. The variable for time, t, represents the number of years the money is left in the account.

Simple Interest

Simple interest is where money is earned based on the initial investment. Simple interest can be calculated by the equation

$\boldsymbol{I = P \cdot r \cdot t}$

I is interest earned, P is the initial investment (or your initial deposit), r is the interest rate (usually substituted in as a decimal), and t is the time in years.

The total repaid, T, then is

$\boldsymbol{T = P + I}$ or, more directly, $\boldsymbol{T = P + (P \cdot r \cdot t)}$

To use the simple interest formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information by listing all four variables and filling in the given information as in the following example.

Example: Simple Interest

You invest $500 in an account that earns 3% per year. What would be your account balance after 15 years?

Solution

You would first need to substitute each of the known values into the equation. Your initial investment is $500 and your time is 15 years. The interest rate is 3% but we must enter it in the equation as a decimal which is 0.03.

$\huge \begin{align*} \boldsymbol{I} &= \boldsymbol{P \cdot r \cdot t} \\ \boldsymbol{I} &= \boldsymbol{\$500 \cdot 0.03 \cdot 15} \\ \boldsymbol{I} &= \boldsymbol{\$225.00} \end{align*}$

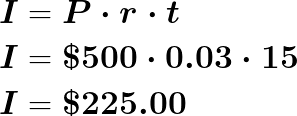
Now, the answer we have calculated is the amount of interest that was earned; not the total account balance after 15 years. In order to find the account balance, you must add the calculated interest to the initial deposit of $500.

Total Account Balance = $500 + $225 = $725

Try it!

#1

Find the simple interest earned after 3 years on $500 at an interest rate of 6%.

Solution

Organize the given information in a list.

I = ?

P = $500.00

r = 6%

t = 3 years

We will use the simple interest formula to find the interest.

Steps

Algebraic

Write the formula.

$I = P \cdot r \cdot t$

Substitute the given information. Remember to write the percent in decimal form.

$I = (500)(0.06)(3)$

Simplify.

$I = \$90.00$

Check your answer. Is $90 a reasonable interest earned on $500 in 3 years?

In 3 years, the money earned is 18%. If we rounded to 20%, the interest would have been 500(0.20) or $100. Yes, $90 is reasonable.

Write a complete sentence that answers the question.

The simple interest is $90.00

#2

Find the rate if a principal of $8,200 earned $3,772 interest in 4 years.

Solution

Organize the given information.

I = $3,772.00

P = $8,200.00

r = ?

t = 4 years.

We will use the simple interest formula to find the rate.

Steps

Algebraic

Write the formula.

$I = P \cdot r \cdot t$

Substitute the given information.

$3,772 = 8,200 \cdot r \cdot 4$

Multiply.

$3,772 = 32,800 \cdot r$

Divide.

$\displaystyle \frac{3,772}{32,800} = \frac{32,800 \cdot r}{32,800}$

Simplify.

$0.115 = r$

Write as a percent.

$11.5\% = r$

Check your answer. Is 11.5% a reasonable rate if $3,772 was earned in 4 years?

$I = P \cdot r \cdot t$

$3{,}772 \stackrel{?}{=} 8,200 \cdot 0.115 \cdot 4$

$3,772 = 3,772 \checkmark$

Write a complete sentence that answers the question.

The rate was 11.5%.

#3

Eduardo noticed that his new car loan papers stated that with an interest rate of 7.5%, he would pay $6,596.25 in interest over 5 years. How much did he borrow to pay for his car?

Solution

We are asked to find the principal, P.

Organize the given information.

I = 6,596.25

P = ?

r = 7.5%

t = 5 years

Steps

Algebraic

Write the formula.

$I = P \cdot r \cdot t$

Substitute the given information.

$6,596.25 = P(0.075)(5)$

Multiply.

$6,596.25 = 0.375 \cdot P$

Divide.

$\displaystyle \frac{6,596.25}{0.375} = \frac{0.375P}{0.375}$

Simplify.

$17,590 = P$

Check your answer. Is $17,590 a reasonable amount to borrow to buy a car?

$I = P \cdot r \cdot t$

—

$6,596.25 \stackrel{?}{=} (17,590)(0.075)(5)$

—

$6,596.25 = 6,596.25 \checkmark$

Write a complete sentence that answers the question.

The amount borrowed was $17,590.

Compound Interest^[3]

As we saw in Simple Interest, an account that pays simple interest only pays based on the original principal and the term of the loan. Accounts offering compound interest pay interest at regular intervals. After each interval, the interest is added to the original principal. Later, interest is calculated on the original principal plus the interest that has been added previously.

After each period, the interest on the account is computed, then added to the account. Then, after the next period, when interest is computed, it is computed based on the original principal AND the interest that was added in the previous periods.

Compound Interest

Compound interest is when you earn interest based on a previous year’s balance. You are essentially earning interest off the investment and any accumulated interest. This is an important difference between the simple interest formula and the compound interest formula because it means that in the compound interest formula a non-linear, or exponential, form is used to calculate it.

B is for Balance (also sometimes called Total amount), P is the initial investment (or your initial deposit), r is the interest rate (usually substituted in as a decimal), and t is the time in years.

$\huge \boldsymbol{B = P(r + 1)^t}$

We can see this equation develop from the simple interest equation by working through the concept step by step.
Let’s say we invest an initial balance of P into an account that pays interest i; then after the first year, the balance would be:

Closing Balance after 1 year = $\boldsymbol{P(1 + i)}$

This is the same as Simple Interest because it only covers a single year. Then, if we take that out and re-invest it for another year – just as you saw us doing in the worked example above – then the balance after the second year will be:

Closing Balance after 2 years = $\boldsymbol{\left[P(1 + i)\right] \times (1 + i) = P(1 + i)^2}$

This is because you will earn interest off of the balance you invested for year two which just so happens to be the initial investment plus the interest you made off of it in year one! If you continue this process, you will have an exponential continuation of the account balance. This is why it is raised to the power of the number of years you invest it.

Try it! – Compound Interest

You invest $500 in an account that earns 3% compounded every year. What would be your account balance after 15 years?

Solution

$\huge \begin{align*} \boldsymbol{B} &= \boldsymbol{P (1 + r)^{t}} \\ \boldsymbol{B} &= \boldsymbol{\$500 (1 + 3\%)^{15}} \\ \boldsymbol{B} &= \boldsymbol{\$500 (1 + 0.03)^{15}} \\ \boldsymbol{B} &= \boldsymbol{\$500 (1.03)^{15}} \\ \boldsymbol{B} &= \boldsymbol{\$778.98} \end{align*}$

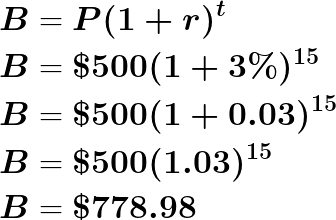
In the above examples, you only see the example when interest is compounded annually. If you are working with a loan that is compounded more frequently the formula may appear as the following:

Compound Interest, compounded n times per year

The future value of an investment, A, when the principal P is invested at an annual interest rate of r (in decimal form), compounded n times per year, for t years, is found using the formula.

$\boldsymbol{A = P\left(1+\frac{r}{n}\right)^{nt}}$

This is also referred to as the future value of the investment.

Try it! – Computing Compound Interest

In the following, compute the Balance or Future Value (A) of the investment with the given conditions.

Principal is $5,000, annual interest rate is 3.8%, compounded annually, for 5 years.
Principal is $18,500, annual interest rate is 6.25%, compounded quarterly, for 17 years.

Solution

The principal is P = $5,000, interest rate, in decimal form, r = 0.038, compounded annually so n = 1, and for t = 5 years. Substituting these values into the first formula, we find

$\begin{align*} B &= P\left(1 + \frac{r}{n} \right)^{nt} \\ B &= 5,000\left(1 + \frac{0.038}{1} \right)^{1 \cdot 5} \\ B &= 5,000(1.038)^{5} \\ B &= 5,000(1.2049) \\ B &= \$6,024.99 \end{align*}$

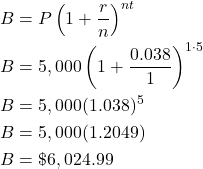
The balance or future value of the investment is $6,044.43.

The principal is P = $18,500, interest rate, in decimal form, r = 0.0625, compounded annually so n = 4, and for t = 17 years. Substituting these values into the first formula, we find

$\begin{align*} B &= P\left(1 + \frac{r}{n} \right)^{nt} \\ B &= 18,500\left(1 + \frac{0.0625}{4} \right)^{4 \cdot 17} \\ B &= 18,500(1 + 0.015625)^{68} \\ B &= 18,500(1.015625)^{68} \\ B &= 18,500(2.86992152) \\ B &= \$53,093.54812 \end{align*}$

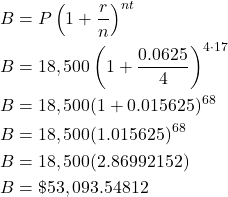
The future value of the investment is $53,093.55.

Key Concepts

Simple interest is represented and calculated with the equation

$\boldsymbol{I = P \cdot r \cdot t}$

Compound interest is represented and calculated with the equation

$\boldsymbol{B = P(1 + r)^t}$ or $\boldsymbol{A = P\left(1+\frac{r}{n}\right)^{nt}}$

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction ; Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
Section material derived by Amanda Towry, Openstax Contemporary math: money matters simple interest and Pre-algebra Percents: Solve simple interest applications ↵
Section material derived by Amanda Towry, Openstax Contemporary math: money matters simple interest ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Simple Interest[2]

Compound Interest[3]

License

Share This Book

Simple Interest^[2]

Compound Interest^[3]