15 More Ratios: Pie charts, Change in Value, DTI
Topics Covered[1]
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
Pie Graphs[2]
Pie graphs can be used to represent parts or percentages of a whole. One of the most common applications of pie graphs is budgets or grade summaries like the one below.
| Quantitative Reasoning Grade Details | |
|---|---|
| Preview/Practice Assignments Average (MML) | 15% |
| Student Portfolio | 25% |
| Mini-Project Average (Blackboard) | 15% |
| Exams Average (3 Total) | 25% |
| Final Exam (Comprehensive) | 20% |
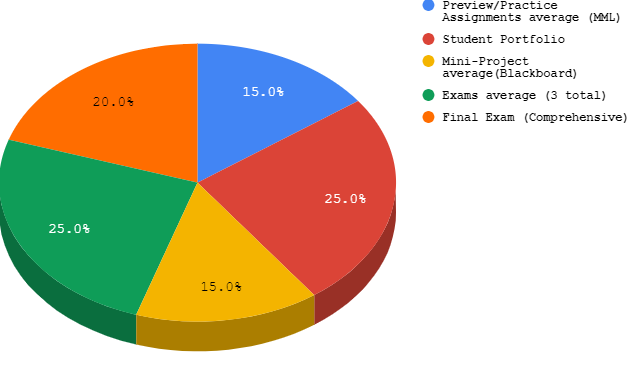
Each percentage of a pie graph is determined by dividing the part of interest by the whole total. When out of a number other than percentages, the pie graph may look something like below:
Part-To-Whole Ratios[3]
Remember that a ratio is a comparison of two numbers or quantities that are measured in the same unit. Part-to-whole ratios are simply a ratio where part or portion of something is compared to the whole.
Example: Part to Whole Ratios
Below is a table showing the budgeted amounts for a student’s monthly bills.
| Expense | Monthly Cost |
|---|---|
| Rent | 500 |
| Utilities | 100 |
| Insurance | 150 |
| Car Loan | 175 |
| Food | 200 |
| Entertainment | 250 |
| Other | 150 |
| Total | $1,525 |
If we were to take part if the budget planned for rent and compare it to the whole in a ratio, it would look like this:
![]()
Part-to-whole ratios allows us to see how a portion compares to a total. If we were to create a pie graph out of the monthly bills data, it would look like the following:
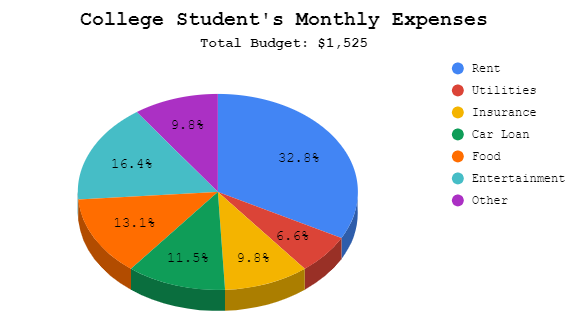
This chart tells us that the portion of the budget is 32% of the total money spent. For every 100 dollars spent each month, 32 dollars and 80 cents are spent on rent.
![]()
Part-To-Part Ratios[4]
Part-to-part ratios are ratios where two separate parts of the same whole are compared to each other.
This makes it easier to compare the importance between two parts or to better understand how they each affect the total.
Example: Part to Part Ratios
Below is the table from example 1 showing the amounts that are budgeted for a student’s monthly bills.
| Expense | Monthly Cost |
|---|---|
| Rent | 500 |
| Utilities | 100 |
| Insurance | 150 |
| Car Loan | 175 |
| Food | 200 |
| Entertainment | 250 |
| Other | 150 |
| Total | $1,525 |
If we were to take the part of the budget reserved for food and the part reserved for rent, how would they compare?

This ratio can be reduced by dividing both the top and bottom by 100, giving the ratio:

This part-to-part ratio comparison tells us that for every 2 dollars spent on food, 5 dollars is spent on rent. This kind of part-to-part comparison lets us see that this college student clearly spends more money on rent than on food; because the rent part (the denominator) is larger than the food part (the numerator).
Working with Numbers in Scientific Notation[5]
When working with REALLY large or small numbers, it is often easier for scientists to write them in scientific notation. Scientific notation is a number usually between 1 and 10 and multiplied by a factor of ten. This allows for fewer digits to be written down when expressing the numbers.
![]()
where ![]() and
and ![]() and n is an integer.
and n is an integer.
Converting from a decimal or a large number to scientific notation is pretty straight forward that only really requires the moving of the decimal point in the number. If the number doesn’t have one (such as a whole integer like 5) you can imagine or write a decimal point at the end of the whole integer.

In both cases, the decimal was moved 3 places to get the first factor, 4, by itself.
- The power of 10 is positive when the number is larger than 1:
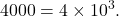
- The power of 10 is negative when the number is between 0 and 1:
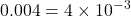 .
.
Try it! – Writing Numbers in Scientific Notation
Write 37,000 in scientific notation.
Solution
| Steps | Solution |
|---|---|
| Step 1: Move the decimal point so that the first factor is greater than or equal to 1 but less than 10. |  |
| Step 2: Count the number of decimal places, n, where the decimal point was moved. | 3.70000 4 places |
| Step 3: Write the number as a product with a power of 10. | |
If the original number is:
|
|
| Step 4: Check. | |
| 104 is 10,000 and 10,000 times 3.7 will be 37,000. | |
Try it! – Writing Numbers in Scientific Notation
Write in scientific notation: 0.0052.
Solution
| Steps | Solution |
|---|---|
| Move the decimal point to get 5.2, a number between 1 and 10. | 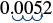 |
| Count the number of decimal places the point was moved. | 3 places |
| Write as a product with a power of 10. | |
| Check your answer:
|
|
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, n, that the decimal point was moved.
- Write the number as a product with a power of 10.
- If the original number is:
- greater than 1, the power of 10 will be
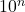 .
. - between 0 and 1, the power of 10 will be
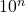 .
.
- greater than 1, the power of 10 will be
- If the original number is:
- Check.
Converting from scientific notation numbers back to decimal notation is just as easy. The decimal is still moved by the number of spaces identified by the exponent on the ten.

In both cases, the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.
Try it! – Convert from Scientific Notation
Convert to decimal form: ![]() .
.
Solution
| Steps | Solutions |
|---|---|
| Step 1: Determine the exponent, n, on the factor 10. | |
| Step 2: Move the decimal point n places, adding zeros if needed. | 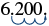 |
|
|
| Step 3: Check to see if your answer makes sense. | |
| 103 is 1000 and 1000 times 6.2 will be 6,200. |
Try it! – Convert from Scientific Notation
Convert to decimal form: ![]() .
.
Solution
| Steps | Solution |
|---|---|
| Determine the exponent n, on the factor 10. | The exponent is −2. |
| Move the decimal point 2 places to the left. |  |
| Add zeros as needed for placeholders. | |
| The Check is left to you. |
How To:
- Determine the exponent, n, on the factor 10.
- Move the decimal n places, adding zeros if needed.
- If the exponent is positive, move the decimal point n places to the right.
- If the exponent is negative, move the decimal point |n| places to the left.
- Check.
Calculating Change In Values[6]
Absolute Change
Absolute change describes the specific change in a quantity or value. It is the difference between a new and old value. It can be calculated as:
![]()
When calculating the absolute change, two situations can occur:
- A POSITIVE difference is an INCREASE over time.
- A NEGATIVE difference is a DECREASE over time.
Try it! – Calculating Absolute Change
A diversified stock portfolio has a worth that changes from $1,500 to $2,250. What is the absolute change in the stock portfolio value?
Solution
We will subtract the old value from the new value. ![]() . Notice that the difference is positive. This means that the change is an increase. As a complete sentence, the answer would be: There was a $750 INCREASE in the stock portfolio value.
. Notice that the difference is positive. This means that the change is an increase. As a complete sentence, the answer would be: There was a $750 INCREASE in the stock portfolio value.
#2 An animal shelter reports that the number of animals awaiting adoption changed from 82 to 46 animals over 6 months. How did the animal population change over time?
Solution
We will subtract the old value from the new value. ![]() . Notice that the difference is negative. This means that the change is a decrease. As a complete sentence, the answer would be: There was a DECREASE of 36 animals in the animal shelter population over 6 months.
. Notice that the difference is negative. This means that the change is a decrease. As a complete sentence, the answer would be: There was a DECREASE of 36 animals in the animal shelter population over 6 months.
Relative Change
Relative change describes the ratio comparison of the absolute change to the original value. It can be calculated as:
![]()
The two possible situations still apply to relative change as they did to absolute change:
- A POSITIVE difference is an INCREASE over time.
- A NEGATIVE difference is a DECREASE over time.
Because the relative change is a ratio, we can multiply it by 100 and report it as a percentage.
Try it! – Calculating Relative Change
A diversified stock portfolio has a worth that changes from $1,500 to $2,250. What is the relative change in the stock portfolio value?
Solution
We will subtract the old value from the new value. ![]() Dividing the result by the old value gives
Dividing the result by the old value gives ![]() .
.
To find the percent, we multiply this result by 100. ![]() .
.
The final answer as a complete sentence would be: The stock portfolio has INCREASED in value by 50%
#2. An animal shelter reports that the number of animals awaiting adoption changed from 82 to 46 animals over 6 months. How did the animal population change over time?
Solution
We will subtract the old value from the new value. ![]() Notice that the difference is negative. Dividing this outcome by the old value gives the result:
Notice that the difference is negative. Dividing this outcome by the old value gives the result: ![]()
To find the percent, we multiply this result by 100. ![]()
The final answer as a complete sentence would be: The number of animals awaiting adoption at the shelter has DECREASED by 78.3% over 6 months.
Debt-To-Income Ratios[7]
One of the major decisions an individual faces when becoming an adult is to take on and manage debt. Debt is what we call when a favor, service, obligation, or money is owed to an individual or organization.
The most common forms of debt for college students are a student or a car loan. When a person is applying for private loans, credit cards, etc. banks will often look at what is called your debt-to-income ratio. Debt-to-income ratio (DTI) is a ratio that compares a person’s monthly debt payments to their gross monthly income.
![]()
Specifically, there are two subcategories of DTI we will look at.
Front-End-DTI is a ratio of housing payments to total income and is used in reference to mortgages.
![]()
Try it! – Front End DTI
Congratulations! You have finished college and have been offered a good job that pays $2,100 per month.
What should your maximum rent payment be to make sure that your front-end DTI is less than or equal to 28%?
Solution
The DTI ratio we are looking for is 28% and so this is the value you plug in for the left side of the equal sign. The monthly income is given as $2,100 which goes in the denominator of the right side of the DTI equation. This gives the following equation to solve:
![]()
First, you need to convert the DTI from a percent to a decimal:
![]()
In order to solve for the unknown rent payment, both sides must be multiplied by the denominator, $2,100:
![]()
Solving by multiplication gives us that the rent payment should be no more than $588
![]()
Try it! – Back End DTI
After taking a job that pays $2,100 per month, you decide to tackle your student loan debt from college. You have built up a student loan debt of $18,500 and they carry a 3.5% interest rate.
Your rent is $500 per month and you pay $150 per month for your brand-new car loan. What should your maximum student loan payment be to maintain a back-end DTI of no more than 32%
Solution
In the back-end DTI equation, all recurring debt payments are considered in the numerator. This means we must consider the money paid for rent, the car loan, and any potential loan payments. Because we are trying to figure out what that student loan payment should be, we can represent it with a variable.
![]()
Next, we will want to convert the 38% to a decimal.
![]()
Next, we want to remove the denominator by multiplying both sides by 2,100.
![]()
Multiplying out the math on the left side of the equal sign and combining like terms on the right results in an equation that can be simply solved by subtraction:
![]()
![]()
Remember that we were looking for the maximum loan payment possible and that is what the variable represents. This means that the loan payment maximum is $148 per month.
Key Concepts
- Absolute change is
New value – Old value
- Relative change is
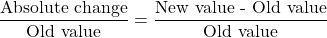
- A number in scientific notation is of the format
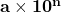
- Debt to income ratio is represented as
DTI=Monthly debt paymentsGross monthly income
- Front-end DTI is represented as
Front-end DTI=Housing payments total income
- Back-end DTI is represented as
Back-end DTI=All recurring debt payments Total income
- Convert from Decimal Notation to Scientific Notation: To convert a decimal to scientific notation:
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, n, that the decimal point was moved.
- Write the number as a product with a power of 10.
- If the original number is greater than 1, the power of 10 will be 10n.
- If the original number is between 0 and 1, the power of 10 will be 10n.
- Check.
- Convert Scientific Notation to Decimal Form: To convert scientific notation to decimal form:
- Determine the exponent, n, on the factor 10.
- Move the decimal n places, adding zeros if needed.
- If the exponent is positive, move the decimal point n places to the right.
- If the exponent is negative, move the decimal point |n| places to the left.
- Check.
- Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
- This material was created by Amanda Towry using the Google Sheets spreadsheet program. ↵
- This material was created by Amanda Towry using Google Sheets spreadsheet and Microsoft Word processing programs. ↵
- This material was created by Amanda Towry using the Microsoft Word processing program. ↵
- Section material derived from Openstax Prealgebra: Polynomials-Integer Exponents and Scientific Notation ↵
- This material was created by Amanda Towry using the Microsoft Word processing program. ↵
- This material was created by Amanda Towry using the Microsoft Word processing program. ↵
A ratio that compares a part or some of the parts of something to the whole.
A ratio that compares a part of a whole to another part of the same whole.
A type of DTI that compares your housing payments, such as rent or mortgage, to your gross monthly income.
A type of DTI that compares all of your recurring debt payments, including rent or mortgage, to your gross monthly income.

