12 Unit Rates and Conversions:
Topics Covered[1]
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
In this section, we will see how to convert among different types of units, such as feet to miles or kilograms to pounds. The basic idea in all of the unit conversions will be to use a form of 1, the multiplicative identity, to change the units but not the value of a quantity.
Write a Rate as a Fraction [2]
Frequently we want to compare two different types of measurements, such as miles to gallons. To make this comparison, we use a rate. Examples of rates are 120 miles in 2 hours, 160 words in 4 minutes, and $5 dollars per 64 ounces.
A rate compares two quantities of different units. A rate is usually written as a fraction.
When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator.
Try it! – Writing Rate as a Fraction
Bob drove his car 525 miles in 9 hours. Write this rate as a fraction.
| Step | Conversion |
|---|---|
| Write as a fraction, with 525 miles in the numerator and 9 hours in the denominator. | 525 miles in 9 hours |
So 525 miles in 9 hours is equivalent to ![]() .
.
Ratios of Two Measurements in Different Units [3]
To find the ratio of two measurements, we must make sure the quantities have been measured with the same unit. If the measurements are not in the same units, we must first convert them to the same units.
We know that to simplify a fraction, we divide out common factors. Similarly in a ratio of measurements, we divide out the common unit.
Try it! – Writing Rate as a Ratio
The Americans with Disabilities Act (ADA) Guidelines for wheel chair ramps require a maximum vertical rise of 1 inch for every 1 foot of horizontal run. What is the ratio of the rise to the run?
| Steps | Conversion |
|---|---|
| Ratio of the rise to the run | |
| Write the ratio as a fraction. | |
| Substitute in the given values. | |
| Convert 1 foot to inches. | |
| Simplify, dividing out common factors and units. |
Find Unit Rates[4]
In the last example, we calculated that Bob was driving at a rate of ![]() . This tells us that every three hours, Bob will travel 175 miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate that has a denominator of 1 unit is referred to as a unit rate.
. This tells us that every three hours, Bob will travel 175 miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate that has a denominator of 1 unit is referred to as a unit rate.
Unit Rate
A unit rate is a rate with a denominator of 1 unit.
Unit rates are very common in our lives. For example, when we say that we are driving at a speed of 68 miles per hour we mean that we travel 68 miles in 1 hour. We would write this rate as 68 miles/hour (read 68 miles per hour). The common abbreviation for this is 68 mph. Note that when no number is written before a unit, it is assumed to be 1.
So 68 miles/hour really means ![]() .
.
Two rates we often use when driving can be written in different forms, as shown:
| Example | Rate | Write | Abbreviate | Read |
|---|---|---|---|---|
| 68 miles in 1 hour | 68 miles/hour | 68 mph | 68 miles per hour | |
| 36 miles to 1 gallon | 36 miles/gallon | 36 mpg | 36 miles per gallon |
Another example of unit rate that you may already know about is hourly pay rate. It is usually expressed as the amount of money earned for one hour of work. For example, if you are paid $12.50 for each hour you work, you could write that your hourly (unit) pay rate is $12.50/hour (read $12.50 per hour.)
To convert a rate to a unit rate, we divide the numerator by the denominator. This gives us a denominator of 1.
Try it! – Determining a Rate
#1
Anita was paid $384 last week for working 32 hours. What is Anita’s hourly pay rate?
| Steps | Conversion |
|---|---|
| Start with a rate of dollars to hours. Then divide. | $384 last week for 32 hours |
| Write as a rate. | |
| Divide the numerator by the denominator. | |
| Rewrite as a rate. | $12/hour |
#2
Sven drives his car 455 miles, using 14 gallons of gasoline. How many miles per gallon does his car get?
| Steps | Conversion |
|---|---|
| 455 miles to 14 gallons of gas | |
| Write as a rate. | |
| Divide 455 by 14 to get the unit rate. |
Make Unit Conversions in the U.S. System[5]
There are two systems of measurement commonly used around the world. Most countries use the metric system. The United States uses a different system of measurement, usually called the U.S. system. We will look at the U.S. system first.
The U.S. system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cups, pints, quarts, and gallons. Both the U.S. system and the metric system measure time in seconds, minutes, or hours.
The equivalencies among the basic units of the U.S. system of measurement are listed in the table below. The table also shows, in parentheses, the common abbreviations for each measurement.
| U.S System Units |
|
|---|---|
| Length | Volume |
| 1 foot (ft) = 12 inches (in)
1 mile (mi) 5280 (ft) 1 yard (yd) = 3 feet (ft) |
3 teaspoons (t) = 1 tablespoon (T)
16 Tablespoons (T) = 1 cup (C) 1 cup (C) = 8 fluid ounces (fl. oz) 1 pint = 2 cups (C) 1 quart (qt) = 2 pints (pt) 1 gallon (gal) = 4 quarts (qt) |
| Weight | Time |
| 1 pound (lb) = 16 ounces (oz)
1 ton = 2000 pounds (lb) |
1 minute (min) = 60 seconds (s)
1 hour (h) = 60 minutes (min) 1 day = 24 hours (h) 1 week (wk) = 7 days 1 year (yr) = 365 days |
In many real-life applications, we need to convert between units of measurement. We will use the identity property of multiplication to do these conversions. We’ll restate the Identity Property of Multiplication here for easy reference.
To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that 1 foot is equal to 12 inches, so we can write 1 as the fraction ![]() . When we multiply by this fraction, we do not change the value but just change the units.
. When we multiply by this fraction, we do not change the value but just change the units.
But ![]() also equals 1. How do we decide whether to multiply by
also equals 1. How do we decide whether to multiply by ![]() or
or ![]() ? We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert 60 inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.
? We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert 60 inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.
![]()
On the other hand, if we wanted to convert 5 feet to inches, we would choose the fraction that has feet in the denominator.
![]()
We treat the unit words like factors and ‘divide out’ common units like we do common factors.
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction, performing the indicated operations and removing the common units.
Try it! – Unit Conversions
Mary Anne is 66 inches tall. What is her height in feet?
| Steps | Conversion |
|---|---|
| Convert 66 inches into feet. | |
| Multiply the measurement to be converted by 1. | |
| Write 1 as a fraction relating the units given and the units needed. | |
| Multiply. | |
| Simplify the fraction. | |
| 5.5 feet |
Notice that the when we simplified the fraction, we first divided out the inches.
Mary Anne is 5.5 feet tall.
When we use the Identity Property of Multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator.
Try it! – Unit Conversions
Ndula, an elephant at the San Diego Safari Park, weighs almost 3.2 tons. Convert her weight to pounds.
(credit: Guldo Da Rozze, Flickr)

Solution
We will convert 3.2 tons into pounds, using the equivalencies in the U.S. System Units table. We will use the Identity Property of Multiplication, writing 1 as the fraction 2000 pounds1 ton.
| Steps | Conversion |
|---|---|
| 3.2 tons | |
| Multiply the measurement to be converted by 1. | |
| Write 1 as a fraction relating to tons and pounds. | |
| Simplify. | |
| Multiply. | 6400 lbs |
| Ndula weighs almost 6,400 pounds. |
Sometimes to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.
Try it! – Unit Conversions
#1
Juliet is going with her family to their summer home. She will be away for 9 weeks. Convert the time to minutes.
| Steps | Conversion |
|---|---|
| 9 weeks | |
| Write 1 as |
|
| Cancel common units. | |
| Multiply. | |
| Juliet will be away for 90,720 minutes. |
#2
How many fluid ounces are in 1 gallon of milk?

| Steps | Conversion |
|---|---|
| 1 gallon | |
| Multiply the measurement to be converted by 1. | |
| Simplify. | |
| Multiply. | |
| Simplify. | 128 fluid ounces |
| There are 128 fluid ounces in a gallon. |
Make Unit Conversions in the Metric System[6]
In the metric system, units are related by powers of 10. The root words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is 1000 meters; the prefix kilo- means thousand. One centimeter is ![]() of a meter, because the prefix centi- means one one-hundredth (just like one cent is
of a meter, because the prefix centi- means one one-hundredth (just like one cent is ![]() of one dollar).
of one dollar).
The equivalencies of measurements in the metric system are shown in the following table. The common abbreviations for each measurement are given in parentheses.
| Metric Measurements |
||
|---|---|---|
| Length | Mass | Volume/Capacity |
| 1 kilometer (km) = 1000 m
1 hectometer (hm) = 100 m 1 dekameter (dam) = 10 m 1 meter (m) = 1 m 1 decimeter (dm) = 0.1 m 1 centimeter (cm) = 0.01 m 1 millimeter (mm) = 0.001 m |
1 kilogram (kg) = 1000 g
1 hectogram (hg) = 100 g 1 dekagram (dag) = 10 g 1 gram (g) = 1 g 1 decigram (dg) = 0.1 g 1 centigram (cg) = 0.01 g 1 milligram (mg) = 0.001 g |
1 kiloliter (kL) = 1000 L
1 hectoliter (hL) = 100 L 1 dekaliter (daL) = 10 L 1 liter (L) = 1 L 1 deciliter (dL) = 0.1 L 1 centiliter (cL) = 0.01 L 1 milliliter (mL) = 0.001 L |
| 1 meter (m) = 100 centimeters (cm)
1 meter (m) = 1000 millimeters (mm) |
1 gram (g) = 100 centigrams (cg)
1 gram (g) = 1000 milligrams (mg) |
1 liter (L) = 100 centiliters (cL)
1 liter (L) = 1000 milliliters (mL) |
To make conversions in the metric system, we will use the same technique we did in the U.S. system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.
Have you ever run a 5 k or 10 k race? The lengths of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.
Try it! – Unit Conversions
#1
Nick ran a 10-kilometer race. How many meters did he run?

| Steps | Conversion |
|---|---|
| 10 kilometers | |
| Multiply the measurement to be converted by 1. | |
| Write 1 as a fraction relating to kilometers and meters. | |
| Simplify. | |
| Multiply. | |
| Nick ran |
#2
Eleanor’s newborn baby weighed 3200 grams. How many kilograms did the baby weigh?
| Steps | Conversion |
|---|---|
| Multiply the measurement to be converted by 1. | |
| Write 1 as a fraction relating kilograms and grams. | |
| Simplify. | |
| Multiply. | |
| Divide. | 3.2 kilograms |
| The baby weighed 3.2 kilograms. |
Since the metric system is based on multiples of ten, conversions involve multiplying by multiples of ten. In Decimal Operations, we learned how to simplify these calculations by just moving the decimal.
To multiply by 10, 100, or 1000, we move the decimal to the right 1, 2, or 3 places, respectively. To multiply by 0.1, 0.01, or 0.001, we move the decimal to the left 1, 2, or 3 places, respectively.
We can apply this pattern when we make measurement conversions in the metric system.
We change 3200 grams to kilograms by multiplying by ![]() (or 0.001). This is the same as moving the decimal 3 places to the left.
(or 0.001). This is the same as moving the decimal 3 places to the left.
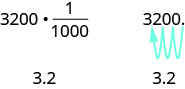 |
Try it! – Unit Conversions
Convert:
a. 350 liters to kiloliters
b. 4.1 liters to milliliters.
| Steps | Conversion |
|---|---|
| 350 L | |
| Multiply by 1, writing 1 as a fraction relating liters to kiloliters. | |
| Simplify. | |
| Move the decimal 3 units to the left. | 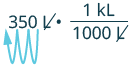 |
| 0.35 kL |
| Steps | Conversion |
|---|---|
| 4.1 L | |
| Multiply by 1, writing 1 as a fraction relating milliliters to liters. | |
| Simplify. | |
| Move the decimal 3 units to the left. |  |
| 4100 mL |
Convert Between U.S. and Metric Systems of Measurement[7]
Many measurements in the United States are made in metric units. A drink may come in 2-liter bottles, calcium may come in 500-mg capsules, and we may run a 5-K race. To work easily in both systems, we need to be able to convert between the two systems.
The following table shows some of the most common conversions.
| Length | Weight | Volume |
|---|---|---|
| 1 in = 2.54 cm
1 ft = 0.305 m 1 yd = 0.914 m 1 mi = 1.61 km 1 m = 3.28 ft |
1 lb = 0.45 kg
1 oz = 28 g 1 kg = 2.2 lb |
1 qt = 0.95 L
1 fl oz = 30 mL 1 L = 1.06 qt |
We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.
Try it! – Unit Conversions
Lee’s water bottle holds 500 mL of water. How many fluid ounces are in the bottle? Round to the nearest tenth of an ounce.
| Steps | Conversion |
|---|---|
| 500 mL | |
| Multiply by a unit conversion factor relating to mL and ounces. | |
| Simplify. | |
| Divide. | 16.7 fl. oz. |
| The water bottle holds 16.7 fluid ounces. |
The conversion factors in the Conversion Factors Between U.S. and Metric Systems table are not exact, but the approximations they give are close enough for everyday purposes. In this exercise, we rounded the number of fluid ounces to the nearest tenth.
Try it! – Unit Conversions
Soleil lives in Minnesota but often travels to Canada for work. While driving on a Canadian highway, she passes a sign that says the next rest stop is in 100 kilometers. How many miles until the next rest stop? Round your answer to the nearest mile.
| Steps | Conversion |
|---|---|
| 100 kilometers | |
| Multiply by a unit conversion factor relating to kilometers and miles. | |
| Simplify. | |
| Divide. | 62 mi |
| It is about 62 miles to the next rest stop. |
Key Concepts
- Making Unit Conversions
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction, performing the indicated operations and removing the common units.
- Conversions within US units
| U.S. System Units | |
|---|---|
| Length | Volume |
| 1 foot (ft) = 12 inches (in)
1 mile (mi) 5280 (ft) 1 yard (yd) = 3 feet (ft) |
3 teaspoons (t) = 1 tablespoon (T)
16 tablespoons (T) = 1 cup (C) 1 cup (C) = 8 fluid ounces (fl oz) 1 pint (pt) = 2 cups (C) 1 quart (qt) = 2 pints (pt) 1 gallon (gal) = 4 quarts (qt) |
| Weight | Time |
| 1 pound (lb) = 16 ounces (oz)
1 ton = 2000 pounds (lb) |
1 minute (min) = 60 seconds (s)
1 hour (h) = 60 minutes (min) 1 day = 24 hours (h) 1 week (wk) = 7 days 1 year (yr) = 365 days |
- Converting within the metric system
| Metric Measurements | ||
|---|---|---|
| Length | Mass | Volume/Capacity |
| 1 kilometer (km) = 1000 m
1 hectometer (hm) = 100 m 1 dekameter (dam) = 10 m 1 meter (m) = 1 m 1 decimeter (dm) = 0.1 m 1 centimeter (cm) = 0.01 m 1 millimeter (mm) = 0.001 m |
1 kilogram (kg) = 1000 g
1 hectogram (hg) = 100 g 1 dekagram (dag) = 10 g 1 gram (g) = 1 g 1 decigram (dg) = 0.1 g 1 centigram (cg) = 0.01 g 1 milligram (mg) = 0.001 g |
1 kiloliter (kL) = 1000 L
1 hectoliter (hL) = 100 L 1 dekaliter (daL) = 10 L 1 liter (L) = 1 L 1 deciliter (dL) = 0.1 L 1 centiliter (cL) = 0.01 L 1 milliliter (mL) = 0.001 L |
| 1 meter = 100 centimeters
1 meter = 1000 millimeters |
1 gram = 100 centigrams
1 gram = 1000 milligrams |
1 liter = 100 centiliters
1 liter = 1000 milliliters |
- Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
- Section material derived from Openstax Prealgebra: Decimals-Ratios and Rate ↵
- Section material derived from Openstax Prealgebra: Decimals-Ratios and Rate ↵
- Section material derived from Openstax Prealgebra: Decimals-Ratios and Rate ↵
- Section material derived from Openstax Prealgebra: The Properties of Real Numbers-Systems of Measurement ↵
- Section material derived from Openstax Prealgebra: The Properties of Real Numbers-Systems of Measurement ↵
- Section material derived from Openstax Prealgebra: The Properties of Real Numbers-Systems of Measurement ↵
A rate compares two quantities of different units. A rate is usually written as a fraction.
A ratio compares two numbers or two quantities that are measured with the same unit. The ratio of a to b is written a to b, a/b, or a:b.
A unit rate is a rate with denominator of 1 unit.
a system of measurement in which units are related by powers of 10.
a system of measurement used in the United States.

