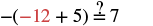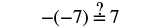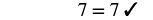"

5 Equations:

Solve Equations Using the Subtraction and Addition Properties of Equality[2]

We began our work solving equations in previous chapters. It has been a while since we have seen an equation, so we will review some of the key concepts before we go any further.

We said that solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that make each side of the equation the same. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle.

Solution of an Equation

A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.

In the earlier sections, we listed the steps to determine if a value is a solution. We restate them here.

How To:

  1. Substitute the number for the variable in the equation.
  2. Simplify the expressions on both sides of the equation.
  3. Determine whether the resulting equation is true.
    • If it is true, the number is a solution.
    • If it is not true, the number is not a solution.

Try it! – Determining Whether a Number is a Solution to an Equation

Determine whether y = 34 is a solution for 4y + 3 = 8y.

Solution

Steps Algebraic
.
. .
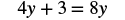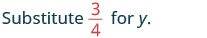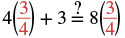Multiply. .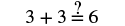
Add. .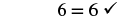

Since y = 34 results in a true equation, 34 is a solution to the equation 4y + 3 = 8y.

The Properties of Addition and Subtraction are as follows:

Subtraction Property of Equality

For all real numbers a, b, and c, if a = b, then a − c = b − c.

Addition Property of Equality

For all real numbers a, b, and c, if a = b, then a + c = b + c.

When you add or subtract the same quantity from both sides of an equation, you still have equality.

We introduced the Subtraction Property of Equality earlier by modeling equations with envelopes and counters. The picture below models the equation x+3=8.

 

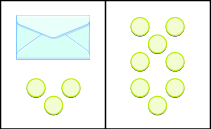
An envelope and three yellow counters are shown on the left side. On the right side are eight yellow counters.

The goal is to isolate the variable on one side of the equation. So, we ‘took away’ 3 from both sides of the equation and found the solution x=5.

Some people picture a balance scale, as in the picture, when they solve equations.

 

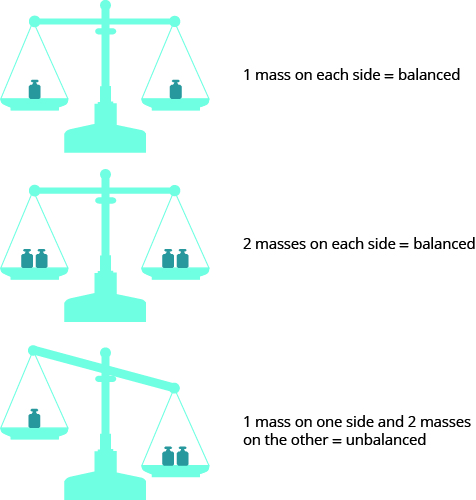
Three balance scales are shown. The top scale has one red weight on each side and is balanced. Beside it is “1 mass on each side equals balanced.” The next scale has two weights on each side and is balanced. Beside it is “2 masses on each side equals balanced.” The bottom scale has one weight on the left and two on the right. The right side is lower than the left. Beside the image is “1 mass on one side and 2 masses on the other equals unbalanced.”

The quantities on both sides of the equal sign in an equation are equal, or balanced. Just as with the balance scale, whatever you do to one side of the equation you must also do to the other to keep it balanced.

Let’s review how to use Subtraction and Addition Properties of Equality to solve equations. We need to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.

Try it! – Solving for a Variable 

Solve: x + 11 = −3.

Solution

To isolate x, we undo the addition of 11 by using the Subtraction Property of Equality.

Steps Algebraic
.
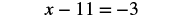Subtract 11 from each side to “undo” the addition. .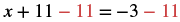
Simplify. .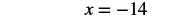
Check: .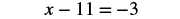
Substitute x = −14. .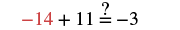
.

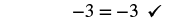Since x = −14 makes x + 11 = −3 a true statement, we know that it is a solution to the equation.

In the original equation in the previous example, 11 was added to the x, so we subtracted 11 to ‘undo’ the addition. In the next example, we will need to ‘undo’ subtraction by using the Addition Property of Equality.

Try it! – Solving for a Variable

Solve: m − 4 = −5.

Solution

Steps Algebraic
.
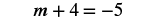Add 4 to each side to “undo” the subtraction. .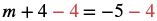
Simplify. .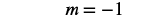
Check: .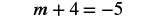
Substitute m = −1. .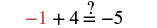
.
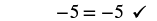The solution to m − 4 = −5 is m = −1.

Now let’s review solving equations with fractions.

Try it! – Solving for a Variable with Fractions 

Solve: n − 38 = 12.

Solution

Steps Algebraic
.
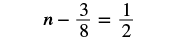Use the Addition Property of Equality. .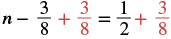
Find the LCD to add the fractions on the right. .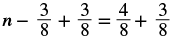
Simplify .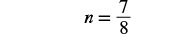
Check: .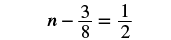
. .
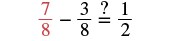Subtract. .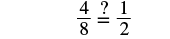
Simplify. .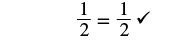
The solution checks.

 We’ll review how to solve equations that contained decimals next.

Try it! – Solving for a Variable with Decimals 

Solve: a − 3.7 = 4.3.

Solution

Steps Algebraic
.
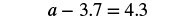Use the Addition Property of Equality. .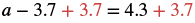
Add. .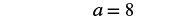
Check: .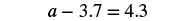
Substitute a=8. .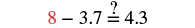
Simplify. .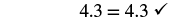
The solution checks.

Solve Equations Using the Division and Multiplication Properties of Equality[3]

First let’s review the Multiplication and Division properties as we prepare to use these properties for solving equations:

Division Property of Equality:

For all real numbers a, b, c, and c ≠ 0, if a = b, then ac = bc.

Multiplication Property of Equality:

For all real numbers a, b, c, if a = b, then ac = bc.

When you divide or multiply both sides of an equation by the same quantity, you still have equality.

Let’s review how these properties of equality can be applied in order to solve equations. Remember, the goal is to ‘undo’ the operation on the variable. In the example below the variable is multiplied by 4, so we will divide both sides by 4 to ‘undo’ the multiplication.

Try it! – Solving for a Variable with Division 

Solve: 4x = −28.

Solution

We use the Division Property of Equality to divide both sides by 4.

Steps Algebraic
.
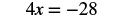Divide both sides by 4 to undo the multiplication. .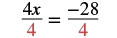
Simplify. .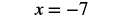
Check your answer. Let x = −7.
.
.
.

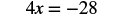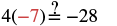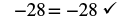Since this is a true statement, x = −7 is a solution to 4x = −28.

In the previous example, to ‘undo’ multiplication, we divided. How do you think we ‘undo’ division?

Try it! – Solving for a Variable with Division 

Solve: a / − 7 = −42.

Solution

Here a is divided by −7. We can multiply both sides by −7 to isolate a.

Steps Algebraic
.
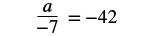Multiply both sides by −7. .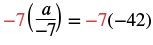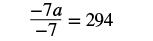

.
Simplify. .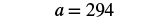
Check your answer. Let a = 294.
.
.
.

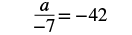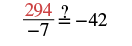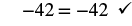In the next example, we see that there are two ways to solve −r = 2. We could multiply both sides by −1.  OR we could take the opposite of both sides. The 2nd option is shown in the Check part of the answer.

#2. Solve: −r = 2.

Solution

Remember −r is equivalent to −1r.

Steps Algebraic
.
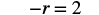Rewrite −r as −1r. .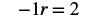
Divide both sides by −1. .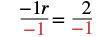
.
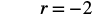Check. .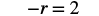
Substitute r = −2 .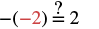
Simplify. .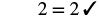

What about if we have a fraction? In the next example we will explore solving using the reciprocal.

Try it! – Solving for a Variable with Fractions 

Solve: 23x = 18.

Solution

Since the product of a number and its reciprocal is 1, our strategy will be to isolate x by multiplying by the reciprocal of 23.

Steps Algebraic
.
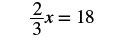Multiply by the reciprocal of 23. .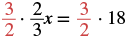
Reciprocals multiply to one. .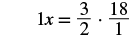
Multiply. .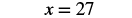
Check your answer. Let x = 27
.
.
.

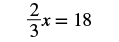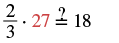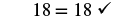Notice that we could have divided both sides of the equation 23x=18 by 23 to isolate x. While this would work, multiplying by the reciprocal requires fewer steps.

Solve Equations with Fraction Coefficients[4]

Let’s use the General Strategy for Solving Linear Equations introduced earlier to solve the equation 18x + 12 = 14.

Steps Algebraic
.
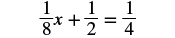To isolate the x term, subtract 12 from both sides. .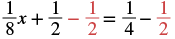
Simplify the left side. .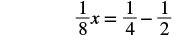
Change the constants to equivalent fractions with the LCD. .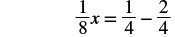
Subtract. .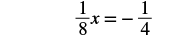
Multiply both sides by the reciprocal of 18. .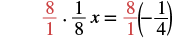
Simplify. .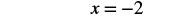

This method worked fine, but many students don’t feel very confident when they see all those fractions. So we are going to show an alternate method to solve equations with fractions. This alternate method eliminates the fractions.

We will apply the Multiplication Property of Equality and multiply both sides of an equation by the least common denominator of all the fractions in the equation. The result of this operation will be a new equation, equivalent to the first, but with no fractions. This process is called clearing the equation of fractions. Let’s solve the same equation again, but this time use the method that clears the fractions.

Try it! – Solving for a Variable with Fractions 

Solve: 18x + 12 = 14.

Solution

Steps Algebraic
Find the least common denominator of all the fractions in the equation. .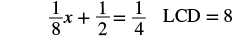
Multiply both sides of the equation by that LCD, 8. This clears the fractions. .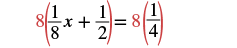
Use the Distributive Property. .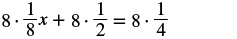
Simplify — and notice, no more fractions! .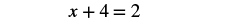
Solve using the General Strategy for Solving Linear Equations. .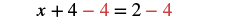
Simplify. .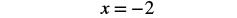
Check: Let x = −2
 .

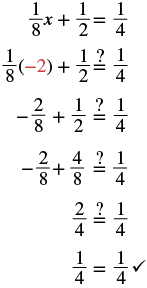Notice in the picture above that once we cleared the equation of fractions, the equation was like those we solved earlier in this chapter. We changed the problem to one we already knew how to solve! We then used the General Strategy for Solving Linear Equations.

How To:

  1. Find the least common denominator of all the fractions in the equation.
  2. Multiply both sides of the equation by that LCD. This clears the fractions.
  3. Solve using the General Strategy for Solving Linear Equations.

Try it! – Solving for a Variable with Fractions

Solve: 7 = 12x + 34x − 23x.

Solution

We want to clear the fractions by multiplying both sides of the equation by the LCD of all the fractions in the equation.

Steps Algebraic
Find the least common denominator of all the fractions in the equation. .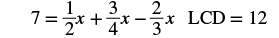
Multiply both sides of the equation by 12. .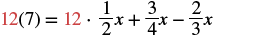
Distribute. .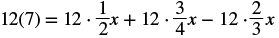
Simplify — and notice, no more fractions! .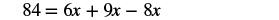
Combine like terms. .
Divide by 7. .
Simplify. .
Check: Let x = 12.
.

 

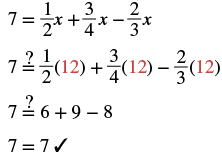In the next example, we’ll have variables and fractions on both sides of the equation.

Try it! – Solving for a Variable with Fractions 

Solve: x + 13 = 16x − 12.

Solution

Steps Algebraic
Find the LCD of all the fractions in the equation. .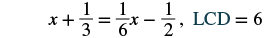
Multiply both sides by the LCD. .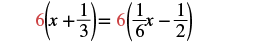
Distribute. .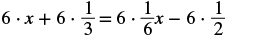
Simplify — no more fractions! .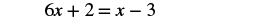
Subtract x from both sides. .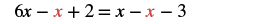
Simplify. .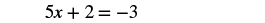
Subtract 2 from both sides. .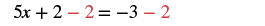
Simplify. .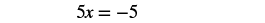
Divide by 5. .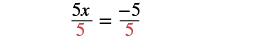
Simplify. .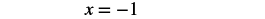
Check: Substitute x = −1.
.

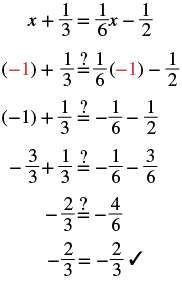In [link], we’ll start by using the Distributive Property. This step will clear the fractions right away!

Try it! – Solving for a Variable with Fractions 

Solve: 1 = 12(4x + 2).

Solution

Steps Algebraic
.
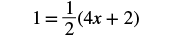Distribute. .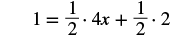
Simplify. Now there are no fractions to clear! .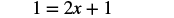
Subtract 1 from both sides. .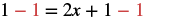
Simplify. .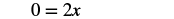
Divide by 2. .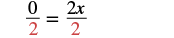
Simplify. .
Check: Let x = 0.
.

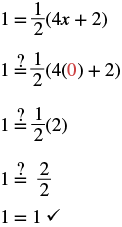Many times, there will still be fractions, even after distributing.

Try it! – Solving for a Variable with Fractions 

Solve: 12(y − 5) = 14(y − 1).

Solution

Steps Algebraic
.
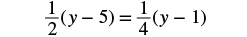Distribute. .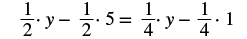
Simplify. .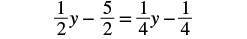
Multiply by the LCD, 4. .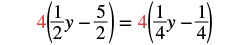
Distribute. .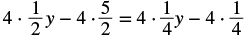
Simplify. .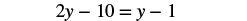
Collect the y terms to the left. .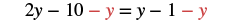
Simplify. .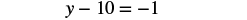
Collect the constants to the right. .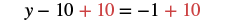
Simplify. .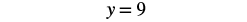
Check: Substitute 9 for y. .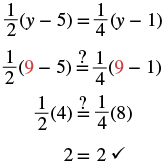

Solve Equations with Decimal Coefficients[5]

Some equations have decimals in them. This kind of equation will occur when we solve problems dealing with money and percent. But decimals are really another way to represent fractions. For example, 0.3 = 310 and 0.17 = 17100. So, when we have an equation with decimals, we can use the same process we used to clear fractions—multiply both sides of the equation by the least common denominator.

Try it! – Solving for a Variable with Decimals 

Solve: 0.8x − 5 = 7.

Solution

The only decimal in the equation is 0.8. Since 0.8=810, the LCD is 10. We can multiply both sides by 10 to clear the decimal.

Steps Algebraic
.
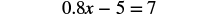Multiply both sides by the LCD. .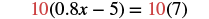
Distribute. .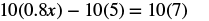
Multiply, and notice, no more decimals! .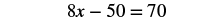
Add 50 to get all constants to the right. .
Simplify. .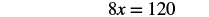
Divide both sides by 8. .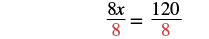
Simplify. .
Check: Let x = 15. .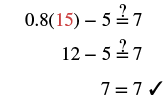

Try it! – Solving for a Variable with Decimals 

Solve: 0.06x + 0.02 = 0.25x − 1.5.

Solution

Look at the decimals and think of the equivalent fractions.

0.06 = 6100, 0.02 = 2100, 0.25 = 25100, 1.5 = 1510

Notice, the LCD is 100.

By multiplying by the LCD, we will clear the decimals.

Steps Algebraic
.
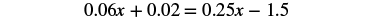Multiply both sides by 100. .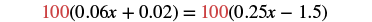
Distribute. .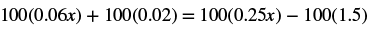
Multiply, and now no more decimals. .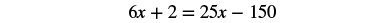
Collect the variables to the right. .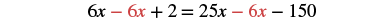
Simplify. .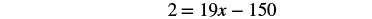
Collect the constants to the left. .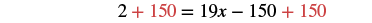
Simplify. .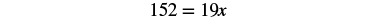
Divide by 19. .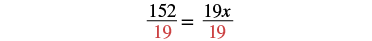
Simplify. .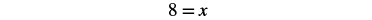
Check: Let x = 8. .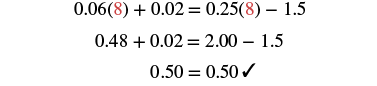

 

The next example uses an equation that is typical of the ones we will see in the money applications in the next chapter. Notice that we will distribute the decimal first before we clear all decimals in the equation.

Try it! – Solving for a Variable with Decimals 

Solve: 0.25x + 0.05(x + 3) = 2.85.

Solution

Steps Algebraic
.
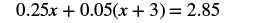Distribute first. .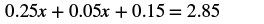
Combine like terms. .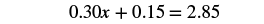
To clear decimals, multiply by 100. .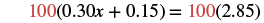
Distribute. .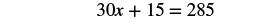
Subtract 15 from both sides. .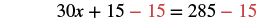
Simplify. .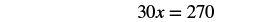
Divide by 30. .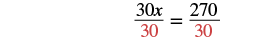
Simplify. .
Check: Let x = 9. .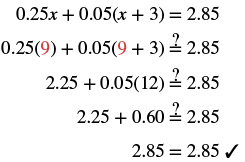

Access Additional Online Resources

Solve Equations Using a General Strategy[6]

Each of the first few sections of this chapter has dealt with solving one specific form of a linear equation. It’s time now to lay out an overall strategy that can be used to solve any linear equation. We call this the general strategy. Some equations won’t require all the steps to solve, but many will. Simplifying each side of the equation as much as possible first makes the rest of the steps easier.

How To:

  1. Simplify each side of the equation as much as possible. Use the Distributive Property to remove any parentheses. Combine like terms.
  2. Collect all the variable terms to one side of the equation. Use the Addition or Subtraction Property of Equality.
  3. Collect all the constant terms to the other side of the equation. Use the Addition or Subtraction Property of Equality.
  4. Make the coefficient of the variable term to equal to 1. Use the Multiplication or Division Property of Equality. State the solution to the equation.
  5. Check the solution. Substitute the solution into the original equation to make sure the result is a true statement.

Try it! – Solving Equations 

Solve: 3(x + 2) = 18.

Solution

Steps Algebraic
.
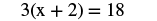Simplify each side of the equation as much as possible.

Use the Distributive Property.		 .
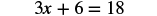Collect all variable terms on one side of the equation—all xs are already on the left side.
Collect constant terms on the other side of the equation.

Subtract 6 from each side		 .
Simplify. .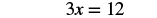
Make the coefficient of the variable term equal to 1. Divide each side by 3. .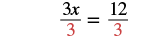
Simplify. .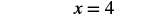
Check: Let x = 4. .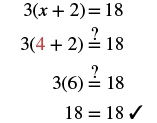

#2 Solve: −(x + 5) = 7.

Solution

Steps Algebraic
.
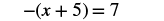Simplify each side of the equation as much as possible by distributing.

The only x term is on the left side, so all variable terms are on the left side of the equation.		 .
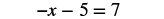Add 5 to both sides to get all constant terms on the right side of the equation. .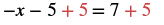
Simplify. .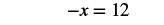
Make the coefficient of the variable term equal to 1 by multiplying both sides by -1. .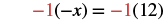
Simplify. .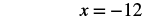
Check: Let x = −12. .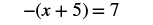

.

.

.

#3 Solve: 4(x − 2) + 5 = −3.

Solution

Steps Algebraic
.
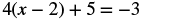Simplify each side of the equation as much as possible.

Distribute.		 .
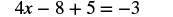Combine like terms .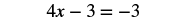
The only x is on the left side, so all variable terms are on one side of the equation.
Add 3 to both sides to get all constant terms on the other side of the equation. .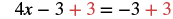
Simplify. .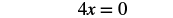
Make the coefficient of the variable term equal to 1 by dividing both sides by 4. .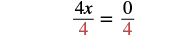
Simplify. .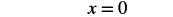
Check: Let x = 0. .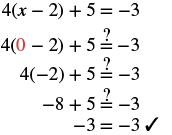

#4 Solve: 8 − 2(3y + 5) = 0.

Solution

Be careful when distributing the negative.

Steps Algebraic
.
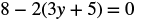Simplify—use the Distributive Property. .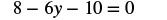
Combine like terms. .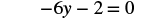
Add 2 to both sides to collect constants on the right. .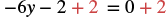
Simplify. .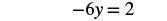
Divide both sides by −6. .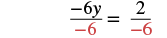
Simplify. .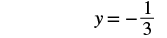
Check: Let y = −13. .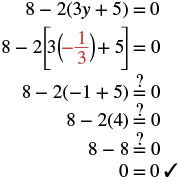

#5. Solve: 3(x − 2) − 5 = 4(2x + 1) + 5.

Solution

Steps Algebraic
.
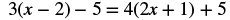Distribute. .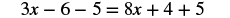
Combine like terms. .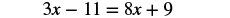
Subtract 3x to get all the variables on the right since 8>3. .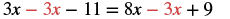
Simplify. .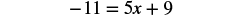
Subtract 9 to get the constants on the left. .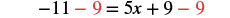
Simplify. .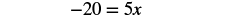
Divide by 5. .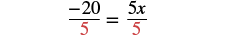
Simplify. .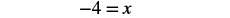
Check: Substitute: −4 = x. .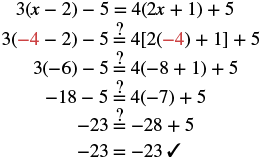

# 6. Solve: 12(6x − 2) = 5 − x.

Solution

Steps Algebraic
.
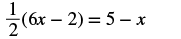Distribute. .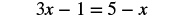
Add x to get all the variables on the left. .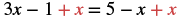
Simplify. .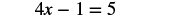
Add 1 to get constants on the right. .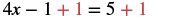
Simplify. .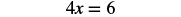
Divide by 4. .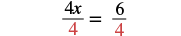
Simplify. .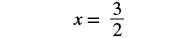
Check: Let x=32. .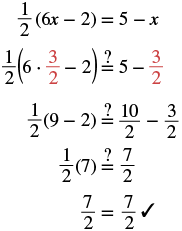

In many applications, we will have to solve equations with decimals. The same general strategy will work for these equations.

Try it! – Solving Equations

Solve: 0.24(100x + 5) = 0.4(30x + 15).

Solution

Steps Algebraic
.
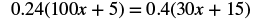Distribute. .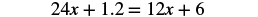
Subtract 12x to get all the xs to the left. .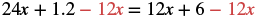
Simplify. .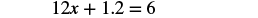
Subtract 1.2 to get the constants to the right. .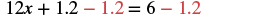
Simplify. .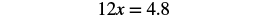
Divide. .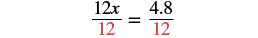
Simplify. .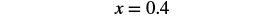
Check: Let x=0.4. .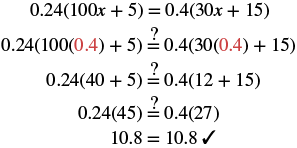

Access Additional Online Resources

Solve Equations That Need to Be Simplified[7]

In the examples up to this point, we have been able to isolate the variable with just one operation. Many of the equations we encounter in algebra will take more steps to solve. Usually, we will need to simplify one or both sides of an equation before using the Subtraction or Addition Properties of Equality. You should always simplify as much as possible before trying to isolate the variable.

Try it! – Simplify and Solve 

Solve: 3x − 7 − 2x − 4 = 1.

Solution

The left side of the equation has an expression that we should simplify before trying to isolate the variable.

Steps Algebraic
.
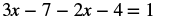Rearrange the terms, using the Commutative Property of Addition. .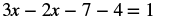
Combine like terms. .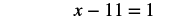
Add 11 to both sides to isolate x. .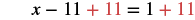
Simplify. .
Check.
 Substitute x=12 into the original equation.
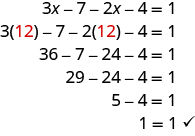 The top line shows 3x minus 7 minus 2x minus 4 equals 1. Below this is 3 times a red 12 minus 7 minus 2 times a red 12 minus 4 equals 1. Next is 36 minus 7 minus 24 minus 4 equals 1. Below is 29 minus 24 minus 4 equals 1. Next is 5 minus 4 equals 1. Last is 1 equals 1.

#2 Solve: 3(n − 4) −2n = −3.

Solution

The left side of the equation has an expression that we should simplify.

Steps Algebraic
.
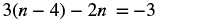Distribute on the left. .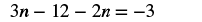
Use the Commutative Property to rearrange terms. .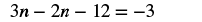
Combine like terms. .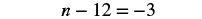
Isolate n using the Addition Property of Equality. .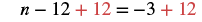
Simplify. .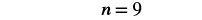
Check.
Substitute n=9 into the original equation.


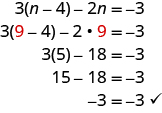 The solution checks.		 The top line says 3 times parentheses n minus 4 minus 2n equals negative 3. The next line says 3 times parentheses red 9 minus 3 minus 2 times red 9 equals negative 3. The next line says 3 times 5 minus 18 equals negative 3. Below this is 15 minus 18 equals negative 3. Last is negative 3 equals negative 3.

#3 Solve: 2(3k − 1) − 5k =−2 − 7.

Solution

Both sides of the equation have expressions that we should simplify before we isolate the variable.

Steps Algebraic
.
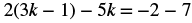Distribute on the left, subtract on the right. .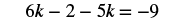
Use the Commutative Property of Addition. .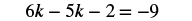
Combine like terms. .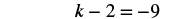
Undo subtraction by using the Addition Property of Equality. .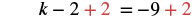
Simplify. .
Check.
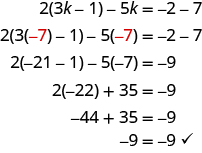Let k = −7.		 The top line says 2 times parentheses 3k minus 1 minus 5k equals negative 2 minus 7. Below this is 2 times parentheses red negative 7 minus 1 minus 5 times red negative 7 equals negative 2 minus 7. The next line says 2 times parentheses negative 21 minus 1 minus 5 times negative 7 equals negative 9. Below that is 2 times negative 22 plus 35 equals negative 9. Next is negative 44 plus 35 equals negative 9. The last line says negative 9 equals negative 9.

 

Key Concepts

  • Determine whether a number is a solution to an equation.
    1. Substitute the number for the variable in the equation.
    2. Simplify the expressions on both sides of the equation.
    3. Determine whether the resulting equation is true.

    If it is true, the number is a solution.

    If it is not true, the number is not a solution.

  • Subtraction and Addition Properties of Equality
    • Subtraction Property of Equality
      For all real numbers a, b, and c,
      if a = b then a – c = b – c.
    • Addition Property of Equality
      For all real numbers a, b, and c,
      if a = b then a + c = b + c.
  • Translate a word sentence to an algebraic equation.
    1. Locate the “equals” word(s). Translate to an equal sign.
    2. Translate the words to the left of the “equals” word(s) into an algebraic expression.
    3. Translate the words to the right of the “equals” word(s) into an algebraic expression.
  • Problem-solving strategy
    1. Read the problem. Make sure you understand all the words and ideas.
    2. Identify what you are looking for.
    3. Name what you are looking for. Choose a variable to represent that quantity.
    4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
    5. Solve the equation using good algebra techniques.
    6. Check the answer in the problem and make sure it makes sense.
    7. Answer the question with a complete sentence.
  • Solve an equation with variables and constants on both sides
    1. Choose one side to be the variable side and then the other will be the constant side.
    2. Collect the variable terms to the variable side, using the Addition or Subtraction Property of Equality.
    3. Collect the constants to the other side, using the Addition or Subtraction Property of Equality.
    4. Make the coefficient of the variable 1, using the Multiplication or Division Property of Equality.
    5. Check the solution by substituting into the original equation.
  • General strategy for solving linear equations
    1. Simplify each side of the equation as much as possible. Use the Distributive Property to remove any parentheses. Combine like terms.
    2. Collect all the variable terms to one side of the equation. Use the Addition or Subtraction Property of Equality.
    3. Collect all the constant terms to the other side of the equation. Use the Addition or Subtraction Property of Equality.
    4. Make the coefficient of the variable term to equal to 1. Use the Multiplication or Division Property of Equality. State the solution to the equation.
    5. Check the solution. Substitute the solution into the original equation to make sure the result is a true statement.
  • Division and Multiplication Properties of Equality
    • Division Property of Equality: For all real numbers a, b, c, and c ≠ 0, if a = b, then \frac{a}{c} = \frac{b}{c}.
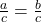    • Multiplication Property of Equality: For all real numbers a, b, c, if a = b, then ac = bc.
  • Solve equations with fraction coefficients by clearing the fractions.
    1. Find the least common denominator of all the fractions in the equation.
    2. Multiply both sides of the equation by that LCD. This clears the fractions.
    3. Solve using the General Strategy for Solving Linear Equations.
  1. Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction; Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction ↵
  2. Section material derived from Openstax Prealgebra: The Language of Algebra-Solving Equations Using the Subtraction and Addition Properties of Equality ↵
  3. Section material derived from Openstax Elementary Algebra: Solving Linear Equations and Inequalities-Solve Equations using the Division and Multiplication Properties of Equality ↵
  4. Section material derived from Openstax Prealgebra: Solving Linear Equations-Solve Equations with Fraction or Decimal Coefficients ↵
  5. Section material derived from Openstax Prealgebra: Solving Linear Equations-Solve Equations with Fraction or Decimal Coefficients ↵
  6. Section material derived from Openstax Prealgebra: Solving Linear Equations-Solve Equations with Variables and Constants on Both Sides ↵
  7. Section material derived from Openstax Prealgebra: The Language of Algebra-Solving Equations Using the Subtraction and Addition Properties of Equality ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0542 Corequisite Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book