"

2 Numbers:

Topics Covered[1]

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

  1. Identify Counting Numbers and Whole Numbers
  2. Identify the Place Value of a Digit
  3. Use Place Value to Name Whole Numbers
  4. Use Place Value to Write Whole Numbers
  5. Round Whole Numbers
  6. Key Concepts

Identify Counting Numbers and Whole Numbers[2]

Learning algebra is similar to learning a language. You start with a basic vocabulary and then add to it as you go along. You need to practice often until the vocabulary becomes easy to you. The more you use the vocabulary, the more familiar it becomes.

Algebra uses numbers and symbols to represent words and ideas. Let’s look at the numbers first. The most basic numbers used in algebra are those we use to count objects: 1,2,3,4,5,… and so on. These are called the counting numbers. The notation “…” is called an ellipsis, which is another way to show “and so on”, or that the pattern continues endlessly. Counting numbers are also called natural numbers.

Counting Numbers

The counting numbers start with 1 and continue.

1, 2, 3, 4, 5…

Counting numbers and whole numbers can be visualized on a number line as shown in the picture below.


An image of a number line from 0 to 6 in increments of one. An arrow above the number line pointing to the right with the label “larger”. An arrow pointing to the left with the label “smaller”.The point labeled 0 is called the origin. The points are equally spaced to the right of 0 and labeled with the counting numbers. When a number is paired with a point, it is called the coordinate of the point.

The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called the whole numbers.

Whole Numbers

The whole numbers are the counting numbers and zero.

0, 1, 2, 3, 4, 5…

We stopped at 5 when listing the first few counting numbers and whole numbers. We could have written more numbers if they were needed to make the patterns clear.

Try it! – Identifying Counting and Whole Numbers 

Which of the following are a. counting numbers? b. whole numbers?

0, \frac{1}{4}, 3, 5.2, 15, 105

Solution
Problem Number Algebraic
a. The counting numbers start at 1, so 0 is not a counting number. The numbers 3, 15, and 105 are all counting numbers.
b. Whole numbers are counting numbers and 0. The numbers 0, 3, 15, and 105 are whole numbers.
The numbers \frac{1}{4} and 5.2 are neither counting numbers nor whole numbers. We will discuss these numbers later.

Identify the Place Value of a Digit [3]

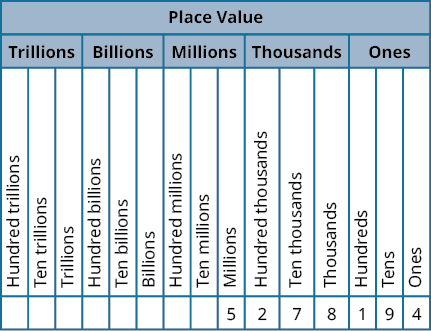
By looking at money and base-10 blocks, we can see that each place in a number has a different value. A place value chart is a useful way to summarize this information. The place values are separated into groups of three, called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.

Just as with the base-10 blocks, where the value of the tens rod is ten times the value of the ones block and the value of the hundreds square is ten times the tens rod, the value of each place in the place-value chart is ten times the value of the place to the right of it.

The table shows how the number 5,278,194 is written in a place value chart.

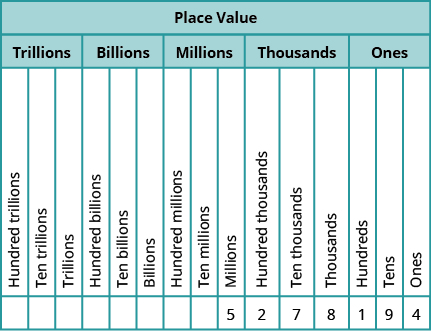
A chart titled 'Place Value' with fifteen columns and 4 rows, with the columns broken down into five groups of three. The header row shows Trillions, Billions, Millions, Thousands, and Ones. The next row has the values 'Hundred trillions', 'Ten trillions', 'trillions', 'hundred billions', 'ten billions', 'billions', 'hundred millions', 'ten millions', 'millions', 'hundred thousands', 'ten thousands', 'thousands', 'hundreds', 'tens', and 'ones'. The first 8 values in the next row are blank. Starting with the ninth column, the values are '5', '2', '7', '8', '1', '9', and '4'.

  • The digit 5 is in the millions place. Its value is 5,000,000.
  • The digit 2 is in the hundred thousands place. Its value is 200,000.
  • The digit 7 is in the ten thousands place. Its value is 70,000.
  • The digit 8 is in the thousands place. Its value is 8,000.
  • The digit 1 is in the hundreds place. Its value is 100.
  • The digit 9 is in the tens place. Its value is 90.
  • The digit 4 is in the ones place. Its value is 4.

Try it! – Identifying Place Value 

In the number 63,407,218; find the place value of each of the following digits:

  1.  7
  2.  0
  3.  1
  4.  6
  5.  3
Solution (click to reveal)

Write the number in a place value chart, starting at the right.


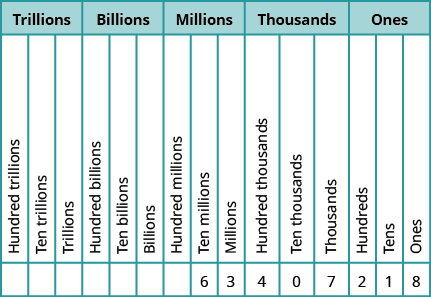
A figure titled “Place Values” with fifteen columns and 2 rows, with the colums broken down into five groups of three. The first row has the values “Hundred trillions”, “Ten trillions”, “trillions”, “hundred billions”, “ten billions”, “billions”, “hundred millions”, “ten millions”, “millions”, “hundred thuosands”, “ten thousands”, “thousands”, “hundreds”, “tens”, and “ones”. The first 7 values in the second row are blank. Starting with eighth column, the values are “6”, “3”, “4”, “0”, “7”, “2”, “1” and “8”. The first group is labeled “trillions” and contains the first row values of “Hundred trillions”, “ten trillions”, and “trillions”. The second group is labeled “billions” and contains the first row values of “Hundred billions”, “ten billions”, and “billions”. The third group is labeled “millions” and contains the first row values of “Hundred millions”, “ten millions”, and “millions”. The fourth group is labeled “thousands” and contains the first row values of “Hundred thousands”, “ten thousands”, and “thousands”. The fifth group is labeled “ones” and contains the first row values of “Hundreds”, “tens”, and “ones”.

Problem Number Algebraic
a The 7 is in the thousands place.
b The 0 is in the ten thousands place.
c The 1 is in the tens place.
d The 6 is in the ten millions place.
e The 3 is in the millions place.

 

Use Place Value to Name Whole Numbers [4]

When you write a check, you write out the number in words as well as in digits. To write a number in words, write the number in each period followed by the name of the period without the ‘s’ at the end. Start with the digit at the left, which has the largest place value. The commas separate the periods, so wherever there is a comma in the number, write a comma between the words. The ones period, which has the smallest place value, is not named.

 

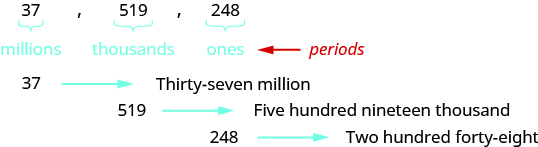
An image with three values separated by commas. The first value is “37” and has the label “millions”. The second value is “519” and has the label thousands. The third value is “248” and has the label ones. Underneath, the value “37” has an arrow pointing to “Thirty-seven million”, the value “519” has an arrow pointing to “Five hundred nineteen thousand”, and the value “248” has an arrow pointing to “Two hundred forty-eight”.

So the number 37,519,248 is written thirty-seven million, five hundred nineteen thousand, two hundred forty-eight.

Notice that the word and is not used when naming a whole number.

How To:

  1. Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.
  2. Use commas in the number to separate the periods.

 

Try it! – Naming a Number

Name the number 8,165,432,098,710 in words.

Solution (click to reveal)
Steps Algebraic
Begin with the leftmost digit, which is 8. It is in the trillions place. eight trillion
The next period to the right is billions. one hundred sixty-five billion
The next period to the right is millions. four hundred thirty-two million
The next period to the right is thousands. ninety-eight thousand
The rightmost period shows the ones. seven hundred ten
An image with five values separated by commas. The first value is “8” and has the label “trillions”. The second value is “165” and has the label “bilions”. The third value is “432” and has the label “millions”. The fourth value is “098” and has the label “thousands”. The fifth value is “710” and has the label “ones”. Underneath, the value “8” has an arrow pointing to “Eight trillion”, the value “165” has an arrow pointing to “One hundred sixty-five billion”, the value “432” has an arrow pointing to “Four hundred thirty-two million”, the value “098” has an arrow pointing to “Ninety-eight thousand”, and the value “710” has an arrow pointing to “seven hundred ten”.

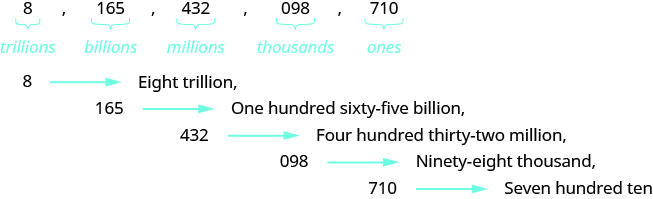
Putting all of the words together, we write 8,165,432,098,710 as eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.

 

Try it! – Name a Number 

A student conducted research and found that the number of mobile phone users in the United States during one month in 2014 was 327,577,529. Name that number in words.

Solution

Identify the periods associated with the number.


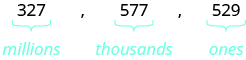An image with three values separated by commas. The first value is “327” and has the label “millions”. The second value is “577” and has the label “thousands”. The third value is “529” and has the label “ones”.Name the number in each period, followed by the period name. Put the commas in to separate the periods.

Period Name
Millions period three hundred twenty-seven million
Thousands period five hundred seventy-seven thousand
Ones period five hundred twenty-nine
So the number of mobile phone users in the Unites States during the month of April was three hundred twenty-seven million, five hundred seventy-seven thousand, five hundred twenty-nine.

Use Place Value to Write Whole Numbers [5]

We will now reverse the process and write a number given in words as digits.

How To:

  1. Identify the words that indicate periods. (Remember the ones period is never named.)
  2. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
  3. Name the number in each period and place the digits in the correct place value position.

 

Try it! – Writing Numbers 

Write the following numbers using digits.

a. fifty-three million, four hundred one thousand, seven hundred forty-two

b. nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine

Solution

Problem Number Explanation
a.

Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Then write the digits in each period.


An image with three blocks of text pointing to numerical values. The first block of text is “fifty-three million”, has the label “millions”, and points to value 53. The second block of text is “four hundred one thousand”, has the label “thousands”, and points to value 401. The third block of text is “seven hundred forty-two”, has the label “ones”, and points to value 742.

Put the numbers together, including the commas. The number is 53,401,742.
b.

Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Then write the digits in each period.


An image with four blocks of text pointing to numerical values. The first block of text is “nine billion”, has the label “billions”, and points to value 9. The second block of text is “two hundred forty-six million”, has the label “millions”, and points to value 246. The third block of text is “seventy-three thousand”, has the label “thousands”, and points to value 742. The fourth block of text is “one hundred eighty-nine”, has the label “ones”, and points to the value 189.

The number is 9,246,073,189.

Notice that in part b., a zero was needed as a placeholder in the hundred thousands place. Be sure to write zeros as needed to make sure that each period, except possibly the first, has three places.

 

Try it! – Writing Numbers

A state budget was about $77 billion. Write the budget in standard form.

Solution

Identify the periods. In this case, only two digits are given, and they are in the billions period. To write the entire number, write zeros for all of the other periods.

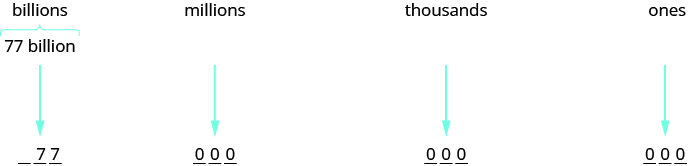
An image with four blocks of text pointing to numerical values. The first block of text is “77 billion”, has the label “billions”, and points to value “77”. The second block of text is null, has the label “millions”, and points to value “000”. The third block of text is null, has the label “thousands”, and points to value “000”. The fourth block of text is null, has the label “ones”, and points to the value “000”.

So, the budget was about $77,000,000,000.

Round Whole Numbers [6]

In 2013, the U.S. Census Bureau reported the population of the state of New York as 19,651,127 people. It might be enough to say that the population is approximately 20 million. The word approximately means that 20 million is not the exact population but is close to the exact value.

The process of approximating a number is called rounding. Numbers are rounded to a specific place value depending on how much accuracy is needed. 20 million was achieved by rounding to the millions place. Had we rounded to the one hundred thousands place, we would have 19,700,000 as a result. Had we rounded to the ten thousands place, we would have 19,650,000 as a result, and so on. The place value to which we round to depends on how we need to use the number.

Using the number line can help you visualize and understand the rounding process. Look at the number line below. Suppose we want to round the number 76 to the nearest ten. Is 76 closer to 70 or 80 on the number line?

An image of a number line from 70 to 80 with increments of one. All the numbers on the number line are black except for 70 and 80 which are red. There is an orange dot at the value “76” on the number line.
We can see that 76 is closer to 80 than to 70. So, 76 rounded to the nearest ten is 80.

Now consider the number 72. Find 72 in the number line below.

An image of a number line from 70 to 80 with increments of one. All the numbers on the number line are black except for 70 and 80 which are red. There is an orange dot at the value “72” on the number line.
We can see that 72 is closer to 70, so, 72 rounded to the nearest ten is 70.

How do we round 75 to the nearest ten. Find 75 in the number line below.

An image of a number line from 70 to 80 with increments of one. All the numbers on the number line are black except for 70 and 80 which are red. There is an orange dot at the value “75” on the number line.
The number 75 is exactly midway between 70 and 80.

So that everyone rounds the same way in cases like this, mathematicians have agreed to round to the higher number, 80. So, 75 rounded to the nearest ten is 80.

Now that we have looked at this process on the number line, we can introduce a more general procedure. To round a number to a specific place, look at the number to the right of that place. If the number is less than 5, round down. If it is greater than or equal to 5, round up.

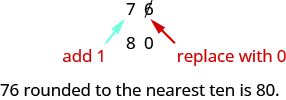
So, for example, to round 76 to the nearest ten, we look at the digit in the ones place.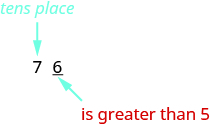An image of value “76”. The text “tens place” is in blue and points to number 7 in “76”. The text “is greater than 5” is in red and points to the number 6 in “76”.The digit in the ones place is a 6. Because 6 is greater than or equal to 5, we increase the digit in the tens place by one. So, the 7 in the tens place becomes an 8. Now, replace any digits to the right of the 8 with zeros. So, 76 rounds to 80.


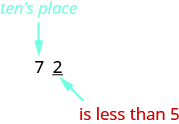An image of the value “76”. The “6” in “76” is crossed out and has an arrow pointing to it which says “replace with 0”. The “7” has an arrow pointing to it that says “add 1”. Under the value “76” is the value “80”.Let’s look again at rounding 72 to the nearest 10. Again, we look to the ones place.An image of value “72”. The text “tens place” is in blue and points to number 7 in “72”. The text “is less than 5” is in red and points to the number 2 in “72”.The digit in the ones place is 2. Because 2 is less than 5, we keep the digit in the tens place the same and replace the digits to the right of it with zero. So 72 rounded to the nearest ten is 70.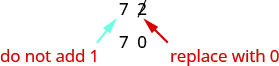An image of the value “72”. The “2” in “72” is crossed out and has an arrow pointing to it which says “replace with 0”. The “7” has an arrow pointing to it that says “do not add 1”. Under the value “72” is the value “70”.

How To:

  1. Locate the given place value. All digits to the left of that place value do not change.
  2. Underline the digit to the right of the given place value.
  3. Determine if this digit is greater than or equal to 5.
    • Yes—add 1 to the digit in the given place value.
    • No—do not change the digit in the given place value.
  4. Replace all digits to the right of the given place value with zeros.

Try it! – Rounding Numbers 

Round 843 to the nearest ten.

Solution

Steps Algebraic
Locate the tens place.
The number 843 with the label “tens place” pointed at the 4 in 843.
Underline the digit to the right of the tens place.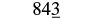
The number 843 with the 3 underlined.
Since 3 is less than 5, do not change the digit in the tens place.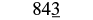
The number 843 with the 3 underlined.
Replace all digits to the right of the tens place with zeros.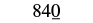
The number 840 with the 0 underlined.
Rounding 843 to the nearest ten gives 840.

#2 Round each number to the nearest hundred:

a. 23,658

b. 3,978

Solution

a.

Steps
 Algebraic
Locate the hundreds place. ..
The digit of the right of the hundreds place is 5. Underline the digit to the right of the hundreds place. ..
Since 5 is greater than or equal to 5, round up by adding 1 to the digit in the hundreds place. Then replace all digits to the right of the hundreds place with zeros. ..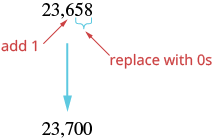
So, 23,658 rounded to the nearest hundred is 23,700.

 

b.

Steps
 Algebraic
Locate the hundreds place. ..
Underline the digit to the right of the hundreds place. ..
The digit to the right of the hundreds place is 7. Since 7 is greater than or equal to 5, round up by added 1 to the 9. Then place all digits to the right of the hundreds place with zeros. ..
So, 3,978 rounded to the nearest hundred is 4,000.

#3 Round each number to the nearest thousand:

a. 147,032

b. 29,504

Solution

a.

Steps
 Algebraic
Locate the thousands place. Underline the digit to the right of the thousands place. ..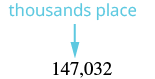
The digit to the right of the thousands place is 0. Since 0 is less than 5, we do not change the digit in the thousands place. ..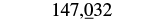
We then replace all digits to the right of the thousands pace with zeros. ..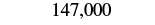
So, 147,032 rounded to the nearest thousand is 147,000.

b.

Steps Algebraic
Locate the thousands place. ..
Underline the digit to the right of the thousands place. ..
The digit to the right of the thousands place is 5. Since 5 is greater than or equal to 5, round up by adding 1 to the 9. Then replace all digits to the right of the thousands place with zeros. ..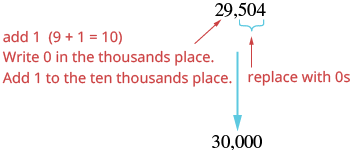
So, 29,504 rounded to the nearest thousand is 30,000.

Notice that in part b., when we add 1 thousand to the 9 thousands, the total is 10 thousands. We regroup this as 1 ten thousand and 0 thousands. We add the 1 ten thousand to the 3 ten thousands and put a 0 in the thousands place.

 

Key Concepts

A chart titled 'Place Value' with fifteen columns and 4 rows, with the columns broken down into five groups of three. The header row shows Trillions, Billions, Millions, Thousands, and Ones. The next row has the values 'Hundred trillions', 'Ten trillions', 'trillions', 'hundred billions', 'ten billions', 'billions', 'hundred millions', 'ten millions', 'millions', 'hundred thousands', 'ten thousands', 'thousands', 'hundreds', 'tens', and 'ones'. The first 8 values in the next row are blank. Starting with the ninth column, the values are '5', '2', '7', '8', '1', '9', and '4'.

  • Name a whole number in words.
    1. Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.
    2. Use commas in the number to separate the periods.
  • Use place value to write a whole number.
    1. Identify the words that indicate periods. (Remember the ones period is never named.)
    2. Draw three blanks to indicate the number of places needed in each period.
    3. Name the number in each period and place the digits in the correct place value position.
  • Round a whole number to a specific place value.
    1. Locate the given place value. All digits to the left of that place value do not change.
    2. Underline the digit to the right of the given place value.
    3. Determine if this digit is greater than or equal to 5. If yes—add 1 to the digit in the given place value. If no—do not change the digit in the given place value.
    4. Replace all digits to the right of the given place value with zeros.

 

  1. Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
  2. Section material derived from Openstax Prealgebra: Introduction-Introduction to Whole Numbers ↵
  3. Section material derived from Openstax Prealgebra: Introduction-Introduction to Whole Numbers ↵
  4. Section material derived from Openstax Prealgebra: Introduction-Introduction to Whole Numbers ↵
  5. Section material derived from Openstax Prealgebra: Introduction-Introduction to Whole Numbers ↵
  6. Section material derived from Openstax Prealgebra: Introduction-Introduction to Whole Numbers ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0542 Corequisite Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book