"

4 Rational Expressions

Topics Covered

Rational Expressions Introduction[1]

We previously reviewed the properties of fractions and their operations. We introduced rational numbers, which are just fractions where the numerators and denominators are integers. In this chapter, we will work with fractions whose numerators and denominators are polynomials. We call this kind of expression a rational expression.

Rational Expression

A rational expression is an expression of the form \displaystyle\frac{p}{q}, where p and q are polynomials and q ≠ 0.

Here are some examples of rational expressions:

Ex. 1 Ex. 2 Ex. 3 Ex. 4
\displaystyle\frac{-24}{56} \displaystyle\frac{5x}{12y} \displaystyle\frac{4x+1}{x^2 - 9} \displaystyle\frac{4x^2 + 3x -1} {2x -8}

Notice that the first rational expression listed above, –\displaystyle\frac{24}{56}, is just a fraction. Since a constant is a polynomial with degree zero, the ratio of two constants is a rational expression, provided the denominator is not zero.

We will do the same operations with rational expressions that we did with fractions. We will simplify, add, subtract, multiply, divide and use them in applications.

Determine the Values for Which a Rational Expression is Undefined

The domain of an expression is the set of numbers for which the expression is defined. If the denominator is zero, the rational expression is undefined. The numerator of a rational expression may be 0—but not the denominator.

When we work with a numerical fraction, it is easy to avoid dividing by zero because we can see the number in the denominator. In order to avoid dividing by zero in a rational expression, we must not allow values of the variable that will make the denominator be zero.

So before we begin any operation with a rational expression, we examine it first to find the values that would make the denominator zero. That way, when we solve a rational equation for example, we will know whether the algebraic solutions we find are allowed or not.

How To: Determine the values for which a rational expression is undefined.
  1. Set the denominator equal to zero.
  2. Solve the equation.

Try It!

Determine the value for which each rational expression is undefined:

a. \displaystyle\frac{8a^2b}{3c}

 b. \displaystyle\frac{4b-3}{2b+5}

c. \displaystyle\frac{x+4}{x^2+5x+6}.

Solution

a.

Solution (click to reveal)
Steps Algebraic
The expression will be undefined when the denominator is zero.    \displaystyle\frac{8a^2b}{3c}
Set the denominator equal to zero and solve for the variable.  3c = 0
Solution c = 0

 

                                                                                                                        

b.

Solution (click to reveal)
Steps Algebraic
Example \displaystyle\frac{4b - 3}{2b + 5}
Set the denominator equal to zero and solve for the variable.        2b + 5 = 0
Simplify       2b = −5
Solution  b = \displaystyle\frac{-5}{2}
b = \displaystyle\frac{4b - 3}{2b + 5} is undefined for b = \displaystyle\frac{-5}{2}.

 

                                                                                                                           

c.

Solution (click to reveal)
Steps Algebraic
Example \displaystyle\frac{x+4} {x^2 + 5x + 6}
Set the denominator equal to zero and solve for the variable. x2 + 5x + 6 = 0
Factor (x + 2)(x + 3) = 0
Set factors equal to zero x + 2 = 0 or x + 3 = 0
Simplify x = −2 or x = −3
\displaystyle\frac{x + 4} {x^2 + 5x + 6} is undefined for x = −2 or x = −3.

 

Simplify Rational Expressions

A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator. Similarly, a simplified rational expression has no common factors, other than 1, in its numerator and denominator.

Simplified Rational Expression

A rational expression is considered simplified if there are no common factors in its numerator and denominator.

For example, \displaystyle\frac{x + 2}{ x + 3} is simplified because there are no common factors of x + 2 and x + 3.  \displaystyle\frac{2x}{3x}  is not simplified because x is a common factor of 2x and 3x.

We use the Equivalent Fractions Property to simplify numerical fractions. We restate it here as we will also use it to simplify rational expressions.

Equivalent Fractions Property

If a, b, and c are numbers where b ≠ 0, c ≠ 0, then

\displaystyle\frac{a}{b} = \displaystyle\frac{a\cdot c}{b\cdot c} and \displaystyle\frac{a\cdot c}{b\cdot c} = \frac{a}{b}.

Notice that in the Equivalent Fractions Property, the values that would make the denominators zero are specifically disallowed. We see b ≠ 0, c ≠ 0 clearly stated.

To simplify rational expressions, we first write the numerator and denominator in factored form. Then we remove the common factors using the Equivalent Fractions Property.

Be very careful as you remove common factors. Factors are multiplied to make a product. You can remove a factor from a product. You cannot remove a term from a sum.

he rational expression is the quantity 2 times 3 times 7 divided by the quantity 3 times 5 times 7 are 3 and 7. Its common factors are 3 and 7, which are factors of the product. When they are removed, the result is two-fifths. The rational expression is the product of 3 x and the quantity x minus 9 divided by the product of 5 and the quantity x minus 9. The common factor is x minus 9, which is a factor of the product. When it is removed, the result is 3 x divided by 5. The rational expression is the quantity x plus 5 divided by 5. There is an x both the numerator and denomiantor. However, it is a term of the sum in the numerator. The rational expression has no common factors.Removing the x’s from \displaystyle \frac{x + 5}{x} would be like cancelling the 2’s in the fraction \displaystyle \frac{2 + 5}{2}!

Try it! – How to Simplify a Rational Expression

Simplify:

\displaystyle\frac{x^2 + 5x + 6} {x^2 + 8x + 12}

Solution

Solution (click to reveal)

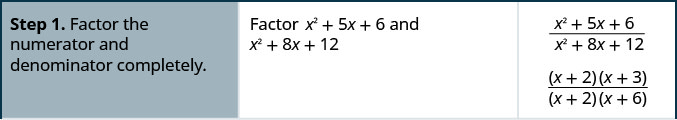
Step 1 is to factor the numerator and denominator completely in the rational expression, the quantity x squared plus 5 x plus six divided by the quantity x squared 8 x plus 12. The numerator, x squared plus 5 x plus six, factors into the quantity x plus 2 times the quantity x plus 3. The denominator, x squared 8 x plus 12, factors into the quantity x plus 2 times the quantity x plus 6.
Step 2 is to simplify the rational expression, the quantity x plus 2 times the quantity x plus 3 all divided by the quantity x plus 2 times the quantity x plus 6, by dividing out the common factor, x plus 6. The result of removing the common factor is the quantity x plus 3 divided by the quantity x plus 6, where x is not equal to 2 and x is not equal to -6.

 

How To: Simplify a rational expression
  1. Factor the numerator and denominator completely.
  2. Simplify by dividing out common factors.

Usually, we leave the simplified rational expression in factored form. This way, it is easy to check that we have removed all the common factors.

Try it!

Simplify: \displaystyle\frac{y^2 + y - 42} {y^2 - 36}.

Solution
Solution (click to reveal)
Steps Algebraic
Factor the numerator and denominator.       \boldsymbol{\displaystyle\frac{(y + 7)(y - 6)} {(y + 6)(y - 6)}}
Remove the common factor y − 6 from the numerator and the denominator. \boldsymbol{\displaystyle\frac{(y + 7)\Ccancel[myred1]{(y - 6)}} {(y + 6)\Ccancel[myred1]{(y - 6)}}}
\boldsymbol{\displaystyle\frac{y + 7} {y + 6}}

 

Now we will see how to simplify a rational expression whose numerator and denominator have opposite factors. We previously introduced opposite notation: the opposite of a is −a and −a = −1 · a.

The numerical fraction, say \displaystyle\frac{7}{-7} simplifies to −1. We also recognize that the numerator and denominator are opposites.

The fraction \displaystyle\frac{a}{-a}, whose numerator and denominator are opposites also simplifies to −1.

Steps Algebraic
Let’s look at the expression b − a. b − a
Rewrite. −a + b
Factor out –1. −1 (a − b)

This tells us that b − a is the opposite of a − b.

In general, we could write the opposite of a − b as b − a. So the rational expression \displaystyle\frac{a - b} {b - a} simplifies to −1.

Opposites in a Rational Expression

The opposite of a − b is b − a.

\displaystyle\frac{a - b} {b - a} = -1  a ≠ b

An expression and its opposite divide to −1.

We will use this property to simplify rational expressions that contain opposites in their numerators and denominators. Be careful not to treat a+b and b+a as opposites. Recall that in addition, order doesn’t matter so a+b = b+a. So if a ≠ −b, then \displaystyle\frac{a + b} {b + a} = 1.

Try it!

Simplify: \displaystyle\frac{x^2 - 4x - 32} {64 - x^2}.

Solution

Solution (click to reveal)
Steps Algebraic
Expression Factor the numerator and denominator of the rational expression, the quantity x squared minus 4 x minus 32 divided by the quantity 64 minus x squared.
Factor the numerator and the denominator. The numerator factors into the quantity x minus 8 times the quantity x plus 4. The denominator factors into the quantity 8 minus x times the quantity 8 plus x.
Recognize the factors that are opposites. The factors x minus 8 and 8 minus x are opposites, so multiply the rational expression by negative 1. The x-8 is shown crossed out.
Simplify. The result is the negative of the quantity x plus 4 divided by the quantity x plus 8.

 

Multiply Rational Expressions

To multiply rational expressions, we do just what we did with numerical fractions. We multiply the numerators and multiply the denominators. Then, if there are any common factors, we remove them to simplify the result.

Multiplication of Rational Expressions

If p, q, r, and s are polynomials where q ≠ 0, s ≠ 0, then

\displaystyle\frac{p}{q} \boldsymbol{\cdot} \frac{r}{s} = \frac{pr}{qs}

  1. Factor each numerator and denominator completely.
  2. Multiply the numerators and denominators.
  3. Simplify by dividing out common factors.

Remember, throughout this chapter, we will assume that all numerical values that would make the denominator be zero are excluded. We will not write the restrictions for each rational expression, but keep in mind that the denominator can never be zero. So in this next example, x ≠ 0, x ≠ 3, and x ≠ 4.

Try it! – How to Multiply Rational Expressions

Simplify:

\displaystyle\frac{2x} {x^2 − 7x + 12} \boldsymbol{\cdot} \frac{x^2 - 9} {6x^2}

Solution
Solution (click to reveal)

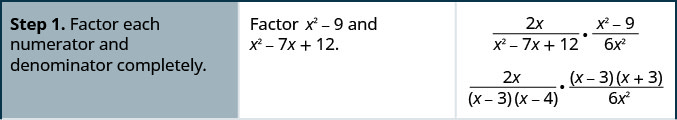
Step 1 is to factor each numerator and the denominator completely in 2 x divided by the quantity x squared minus 7 x plus 12 times the rational expression the quantity x squared minus 9 divided by 6 x squared. The denominator, x squared minus 7 x plus 12, factors into the quantity x minus 3 times the quantity x minus 4. The numerator x squared minus 9 factors into the quantity x minus 3 times the quantity x plus 3.
Step 2 is to multiply the numerators 2 x and the quantity x minus 3 times the quantity x plus 3, and the denominators the quantity x minus 3 times the quantity x minus 4 and 6 x squared. It is helpful to write the monomials in the numerator and in the denominator. first.
Step 3 is to simplify 2 x times the quantity x minus 3 times the quantity x plus 3 all divided by 2 times 3 times x times x times the quantity x minus 3 times the quantity x plus 4 by dividing out the common factor, x minus 3. Leaving the denominator in factored form, the result is the quantity x plus 3 divided by 3 x times the quantity x minus 4.

 

The following is an alternate method, used in the College Algebra textbook, where you divide out the common factors prior to multiplying the numerators and denominators.

#2 Multiply:

\displaystyle\frac{3a^2 - 8a - 3} {a^2 − 25} \boldsymbol{\cdot} \frac{a^2 + 10a + 25} {3a^2 - 14a - 5}

Solution

Solution (click to reveal)
Steps Algebraic
Factor numerators and Denominators \boldsymbol{\displaystyle \frac{(3 a + 1)(a - 3)}{(a - 5)(a + 5)} \cdot \frac{(a + 5)(a + 5)}{(3a + 1)(a - 5)}}
Divide Common Factors \boldsymbol{\displaystyle \frac{\Ccancel[myred1]{(3a + 1)}(a - 3)}{(a - 5)\Ccancel[myred1]{(a + 5)}} \cdot \frac{\Ccancel[myred1]{(a + 5)}(a + 5)}{\Ccancel[myred1]{(3a + 1)}(a - 5)}}
V2 not bold \displaystyle \frac{\Ccancel[myred1]{(3a + 1)}(a - 3)}{(a - 5)\Ccancel[myred1]{(a + 5)}} \cdot \frac{\Ccancel[red]{(a + 5)}(a + 5)}{\Ccancel[red]{(3a + 1)}(a - 5)}}
Simplify \boldsymbol{\displaystyle \frac{(a - 3)}{(a - 5)} \cdot \frac{(a + 5)}{(a - 5)}}
Multiply remaining Factors in numerators \boldsymbol{\displaystyle \frac{(a - 3)(a + 5)}{(a - 5)^2} a \neq 5,-5,-\frac{1}{3}}

 

Divide Rational Expressions

Just like we did for numerical fractions, to divide a rational expression by another, multiply the first expression by the reciprocal of the second. Using this approach, we would rewrite \displaystyle\frac{1}{x} ÷ \displaystyle\frac{x^2}{3} as the product \displaystyle\frac{1}{x} • \displaystyle\frac{3}{x^2}.  Once the division expression has been rewritten as a multiplication expression, we can multiply as we did before.

Division of Rational Expressions

If p, q, r, and s are polynomials where q ≠ 0, r ≠ 0, s ≠ 0, then

\displaystyle\frac{p}{q} \boldsymbol{\div} \frac{r}{s} = \frac{p}{q}\boldsymbol{\cdot}\frac{s}{r}

  1. Rewrite the division as the product of the first rational expression and the reciprocal of the second.
  2. Factor the numerators and denominators completely.
  3. Multiply the numerators and denominators together.
  4. Simplify by dividing out common factors.

Once we rewrite the division as multiplication of the first expression by the reciprocal of the second, we then factor everything and look for common factors.

Try it! – How to Divide Rational Expressions

Divide: \displaystyle\frac{p^3 + q^3} {2p^2 + 2pq + 2q^2} ÷ \displaystyle\frac{p^2 - q^2} {6}.

Solution
Solution (click to reveal)

Step 1 is to rewrite the division of the rational expression, the quantity p cubed plus q cubes divided by the quantity 2 p squared plus 2 p q plus 2 q squared divided by the rational expression, the quantity p squared minus q squared all divided by 6. Do this by flipping the rational expression, the quantity p squared minus q squared all divided by 6, and changing division to multiplication. The result is the quantity p cubed plus q cubes divided by the quantity 2 p squared plus 2 p q plus 2 q squared times the quantity 6 divided by the quantity p squared minus q squared.
Step 2 is to factor the numerators, the quantity p cubed plus q cubed and 6, and the denominators, the quantity 2 p squared plus 2 p q plus 2 squared and the quantity p squared minus q squared, completely. The result is the quantity p plus q times the quantity p squared minus p q plus q squared all times the quantity 2 times 3 divided by the quantity p minus q times the quantity p plus q.
Step 3 is to multiply the numerators and denominators. The result is the quantity p plus q times the quantity p squared minus p q plus q squared times 2 times 3 all divided by the 2 times the quantity p squared plus p q plus q squared times the quantity p minus q times the quantity p plus q.
Step 4 is to simplify the expression by dividing out the common factors, the quantity p plus q and 2. The result is 3 times the quantity p squared minus p q plus q squared all divided by the quantity p minus q times the quantity p squared plus p q plus q squared.

 

The following is an alternate method, used in the College Algebra textbook, where you divide out the common factors prior to multiplying the numerators and denominators.

Try it! – Dividing Rational Expressions

Divide the rational expressions and express the quotient in simplest form:

\displaystyle\frac{2x^2 + x - 6} {x^2 - 1} ÷ \displaystyle\frac{x^2 - 4} {x^2 + 2x + 1}

Solution

Solution (click to reveal)
Steps Algebraic
Factor numerators and Denominators \boldsymbol{\displaystyle \frac{(2x^2 + x + 6)}{(x^2 - 1)} \cdot \frac{(x^2 + 2 +- 15)}{(x^2 + 4))}}
Divide Common Factors \boldsymbol{\displaystyle \frac{\Ccancel[myred1]{(3a + 1)}(a - 3)}{(a - 5)\Ccancel[myred1]{(a + 5)}} \cdot \frac{\Ccancel[myred1]{(a + 5)}(a + 5)}{\Ccancel[myred1]{(3a + 1)}(a - 5)}}
Simplify \boldsymbol{\displaystyle \frac{(a - 3)}{(a - 5)} \cdot \frac{(a + 5)}{(a - 5)}}
Multiply remaining Factors in numerators \boldsymbol{\displaystyle \frac{(a - 3)(a + 5)}{(a - 5)^2} a \neq 5,-5,-\frac{1}{3}}

 

Add and Subtract Rational Expressions

What is the first step you take when you add numerical fractions? You check if they have a common denominator. If they do, you add the numerators and place the sum over the common denominator. If they do not have a common denominator, you find one before you add.

It is the same with rational expressions. To add rational expressions, they must have a common denominator. When the denominators are the same, you add the numerators and place the sum over the common denominator.

Rational Expression Addition and Subtraction

If p, q, and r are polynomials where r ≠ 0, then

\displaystyle\frac{p}{r} + \frac{q}{r} = \frac{p+q}{r} and \displaystyle\frac{p}{r} - \frac{q}{r} = \frac{p - q}{r}

How To:
  • To add or subtract rational expressions with a common denominator, add or subtract the numerators and place the result over the common denominator.
  • We always simplify rational expressions. Be sure to factor, if possible, after you subtract the numerators so you can identify any common factors.
  • Remember, too, we do not allow values that would make the denominator zero.

Try it!

Add: \displaystyle\frac{11x + 28} {x + 4} + \displaystyle\frac{x^2} {x + 4}

Solution

Solution (click to reveal)

Since the denominator is x + 4 we must exclude the value x = −4.

Steps Algebraic
Original problem \boldsymbol{\displaystyle\frac{11x + 28} {x + 4}} + \boldsymbol{\displaystyle\frac{x^2} {x + 4}}, x ≠ −4
The fractions have a common denominator, so add the numerators and place the sum over the common denominator. \boldsymbol{\displaystyle\frac{11x + 28 + x^2} {x + 4}}
Write the degrees in descending order. \boldsymbol{\displaystyle\frac{x^2 + 11x + 28} {x + 4}}
Factor the numerator. \boldsymbol{\displaystyle\frac{(x + 4)(x + 7)} {x + 4}}
Simplify by removing common factors. \boldsymbol{\displaystyle\frac{\Ccancel[myred1]{(x + 4)}(x + 7)} {\Ccancel[myred1]{x + 4}}}
Simplify. x + 7

The expression simplifies to x + 7 but the original expression had a denominator of x + 4  so x ≠ −4.

To subtract rational expressions, they must also have a common denominator. When the denominators are the same, you subtract the numerators and place the difference over the common denominator. Be careful of the signs when you subtract a binomial or trinomial.

Try it!

Subtract: \displaystyle\frac{5x^2 - 7x + 3} {x^2 - 3x + 18} – \displaystyle\frac{4x^2 + x - 9} {x^2 -3x + 18}.

Solution

Solution (click to reveal)
Steps Algebraic
Original Problem  \displaystyle\frac{5x^2 - 7x + 3} {x^2 - 3x + 18} – \displaystyle\frac{4x^2 + x - 9} {x^2 - 3x + 18}
Subtract the numerators and place the difference over the common denominator  \displaystyle\frac{5x^2 - 7x + 3-(4x^2 + x - 9)} {x^2 - 3x + 18}
Distribute the sign in the numerator. \displaystyle\frac{5x^2 - 7x + 3 - 4x^2 - x + 9} {x^2 - 3x - 18}
Combine like terms. \displaystyle\frac{x^2 - 8x + 12} {x^2 - 3x - 18}
Factor the numerator and the denominator. \displaystyle\frac{(x - 2)(x - 6)} {(x + 3)(x - 6)}
Simplify by removing common factors. \displaystyle\frac{(x - 2)\Ccancel[myred1]{(x - 6)}} {(x + 3)\Ccancel[myred1]{(x - 6)}}
Solution: \displaystyle\frac{(x - 2)} {(x + 3)}

Add, Subtract with Unlike Denominators

Adding and subtracting rational expressions works just like adding and subtracting numerical fractions. To add fractions, we need to find a common denominator. Let’s look at an example of fraction addition.

Steps
 \displaystyle\frac{5} {24} + \frac{1} {40} = \frac{25} {120} + \frac{3} {120}
= \displaystyle\frac{28} {120}
= \displaystyle\frac{7} {30}

We have to rewrite the fractions so they share a common denominator before we are able to add. We must do the same thing when adding or subtracting rational expressions.

The easiest common denominator to use will be the least common denominator, or LCD. The LCD is the smallest multiple that the denominators have in common. To find the LCD of two rational expressions, we factor the expressions and multiply all of the distinct factors. For instance, if the factored denominators were (x + 3)(x + 4) and (x + 4)(x + 5), then the LCD would be (x + 3)(x + 4)(x + 5).

How to: Find the least common denominator of rational expressions.
  1. Factor each denominator completely.
  2. List the factors of each denominator. Match factors vertically when possible, as this will make it easier to avoid duplication.
  3. Bring down the columns by including all factors, but do not include common factors twice.
  4. Write the LCD as the product of the factors.

Remember, we always exclude values that would make the denominator zero. What values of x should we exclude in this next example?

Try it!

a. Find the LCD for the expressions \displaystyle\frac{8} {x^2 - 2x - 3}, \displaystyle\frac{3x} {x^2 + 4x + 3} and b. rewrite them as equivalent rational expressions with the lowest common denominator.

Solution

a.

Solution (click to reveal)
Steps Algebraic
Example \displaystyle\frac{8} {x^2 - 2x - 3}, \displaystyle\frac{3x} {x^2 + 4x + 3}.
Factor each denominator completely, lining up common factors.

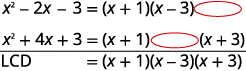Bring down the columns.		 Find the lowest common denominator of the rational expressions 8 divided by the quantity x squared minus 2 x minus 3 and 3 x divided by the quantity x squared plus 4 x plus 3. Line up the denominators and factor them completely. Line up the common factors. The denominator x squared minus 2 x minus 3 is equal to the quantity x plus 1 times the quantity x minus 3. The denominator x squared plus 4 x plus 3 is equal to the quantity x plus 1 times the quantity x plus 3. The quantity x plus 1 is a factor of both denominators. The quantity x minus 3 is only a factor of the denominator x squared minus 2 x minus 3, so it is in a column alone. The quantity x plus 3 is only a factor of the denominator x squared plus 4 x plus 3, so it is in a column alone. T
Write the LCD as the product of the factors. he lowest common denominator is the product of the primes from each column, the quantity x plus 1 times the quantity x minus 3 times the quantity x plus 3.

 

b.

Solution (click to reveal)
Steps Algebraic
Example Factor the denominators of the rational expressions, 8 divided by the quantity x squared minus 2 x minus 3 and 3 x divided by the quantity x squared plus 4 x plus 3.
Factor each denominator. The denominator, x squared minus 2 x minus 3, factors into the quantity x plus 1 times the quantity x minus 3. The denominator, x squared plus 4 x plus 3, factors into the quantity x plus 1 times the quantity x plus 3. Write each rational expression with a factored denominator. The first rational expression is 8 divided by the quantity x plus 1 times the quantity x minus 3. The second rational expression is 3 x divided by the quantity x plus 1 times the quantity x plus 3.
Multiply each denominator by the ‘missing’
LCD factor and multiply each numerator by the same factor.		 Multiply the numerator and denominator of each expression by the missing lowest common denominator factor. The results are 8 times the quantity x plus 3 all divided by the quantity x plus 1 times the quantity x minus 3 times the quantity x plus 3 and the quantity 3 x times the quantity x minus 3 all divided by the quantity x plus 1 times the quantity x plus 3 times the quantity x minus 3.
Simplify the numerators. Simplify the numerators of the rational expressions and keep the denominators. 8 times the quantity x plus 3 is 8 x plus 24. 3 x times the quantity x minus 3 is 3 x squared minus 9. The results are 8 times the quantity x plus 3 all divided by the quantity x plus 1 times the quantity x minus 3 times the quantity x plus 3 and the quantity 3 x squared minus 9 x all divided by the quantity x plus 1 times x plus 3 times the quantity x minus 3.

 

Try it!

a. Find the LCD for the expressions \displaystyle\frac{3x} {x^2 - 3x - 10}, \displaystyle\frac{5} {x^2 + 3x + 2} b. rewrite them as equivalent rational expressions with the lowest common denominator.

Solution

a.

Solution (click to reveal)

(x + 2)(x − 5)(x + 1)

b.

Solution (click to reveal)

\displaystyle\frac{3x^2 + 3x} {(x + 2)(x - 5)(x + 1)},

\displaystyle\frac{5x - 25} {(x + 2)(x - 5)(x + 1)}

Now we have all the steps we need to add or subtract rational expressions with unlike denominators. Here’s an example:

  1. Determine if the expressions have a common denominator.
    • Yes – go to step 2.
    • No – Rewrite each rational expression with the LCD.
      • Find the LCD.
      • Rewrite each rational expression as an equivalent rational expression with the LCD.
  2. Add or subtract the rational expressions.
  3. Simplify, if possible.

 

Try it!

Add: \displaystyle\frac{3} {x - 3} – \displaystyle\frac{2} {x - 2}.

Solution

Solution (click to reveal)

Step 1 is to determine if the rational expressions 3 divided by the quantity x minus 3 and 2 divided by the quantity x minus 2 have a common factors. The denominators x minus 3 and x minus 2 do not have any common factors, which means the lowest common denominator of the rational expressions is the quantity x minus 3 times the quantity x minus 2. Rewrite each rational expression with the least common denominator. Multiply the numerator and denominator of 3 divided by the quantity x minus 3 by the quantity x minus 2. Multiply the numerator and denominator of 2 divided by the quantity x minus 2 by the quantity x minus 2. The result is the rational expression 3 times the quantity x minus 2 all divided by the quantity x minus 3 times the quantity x minus 2 plus the rational expression 2 times the quantity x minus 3 divided by the quantity x minus 2 times the quantity x minus 3. Simplify the numerators and keep the denominators factored. The numerator of the first rational expression, 3 times the quantity x minus 2, simplifies to 3 x minus 6. The numerator of the second rational expression, 2 times the quantity x minus 3, simplifies to 2 x minus 6. The result is the rational expression the quantity 3 x minus 6 all divided by the quantity x minus 3 times the quantity x minus 2 plus the rational expression, the quantity 2 x minus 6 all divided by the quantity x minus 3 times the quantity x minus 2.
Step 2 is to add or subtract the rational expressions by adding the numerators, the quantity 3 x minus 6 and the quantity 2 x minus 6, and placing the sum over the denominator, the quantity x minus 3 times the quantity x minus 2. The result is the quantity 3 x minus 6 plus 2 x minus 6 all divided by the quantity x minus 3 times the quantity x minus 2. Simplify the numerator by combining like terms. The result is the quantity 5 x minus 12 all divided by the quantity x minus 3 times the quantity x minus 2.
Step 3. Notice that 5 x minus 12 cannot be factored, so the answer is simplified.

2. Subtract:

\displaystyle\frac{-3n - 9} {n^2 + n - 6} – \displaystyle\frac{n +3 } {2 - n}.

Solution

Solution (click to reveal)
Steps Algebraic
Original Equation Subtract the rational expressions the quantity negative 3 n minus 9 all divided by the quantity n squared plus n minus 6 and the quantity n plus 3 divided by the quantity 2 minus n.
Factor the denominator. Factor the denominator of the first rational expression, n squared plus n minus 6. The result is the quantity negative 3 n minus 9 all divided by the quantity n minus 2 times the quantity n plus 3 minus the quantity n plus 3 divided by the quantity 2 minus n. Notice that n minus 2 and 2 minus n are opposites.
Since n − 2 and 2 − n are opposites, we will multiply the second rational expression by −1. Multiply the numerator and denominator of the second rational expression, n plus 3 divided by the quantity 2 minus n, by negative 1. Write its denominator, negative 1 times the quantity 2 minus n, as n minus 2. The result is the quantity negative 3 n minus 9 all divided by the quantity n minus 2 times the quantity n plus 3 minus negative one times the quantity n plus 3 all divided by n minus 2.
Write (-1) (2-n) as n-2. Simplify the numerator of the second rational expression, remembering that a minus negative b is a plus b. Write the numerator, negative one times the quantity n plus 3, over n minus 2.
Simplify. Remember, a − (−b) = a + b The result is the quantity negative 3 n minus 9 all divided by the quantity n minus 2 times the quantity n plus 3 minus the quantity n plus 3 all divided by n minus 2. Notice that the denominators do not have any common factors.
Do the rational expressions have a common denominator? No.
Find the LCD (n − 2)(n + 3)
Rewrite each rational expression as an
equivalent rational expression with the LCD.		 Find the lowest common denominator. The denominator, n squared plus n minus 6, factors into the quantity n minus 2 times the quantity n plus 3. The denominator, n minus 2, cannot be factored. Line the denominators up by common factors. The least common denominator is the product of a factor from each column, the quantity n minus 2 times the quantity n plus 3. Rewrite each rational expression as an equivalent rational expression using the lowest common denominator. The first rational expression, the quantity negative 3 n minus 9 all divided by the quantity n minus 2 times the quantity n plus 3 , is already written using the LCD. Multiply the numerator and denominator of the second rational expression, the quantity n plus 3 divided by the quantity n plus 2, by n plus 3.
Simplify the numerators. Simplify the numerators. The result is the quantity negative 3 n minus 9 all divided by the quantity n minus 2 times the quantity n plus 3 minus the quantity n squared plus 6 n plus 9 all divided by the quantity n minus 2 times the quantity n plus 3.
Add the rational expressions. Add the rational expressions. The result is the quantity negative 3 n minus 9 plus n squared plus 6 n plus 9 all divided by the quantity n minus 2 times the quantity n plus 3.
Simplify the numerator. Simplify the numerator by combining like terms. The result is the quantity n squared plus 3 n all divided by the quantity n minus 2 times the quantity n plus 3.
Factor the numerator to look for common factors. Factoring the numerator, results in n times the quantity n plus 3 all divided by the quantity n minus 2 times the quantity n plus 3. Notice that n plus 3 is a common factor in the numerator and denominator. Remove it and simplify.
Simplify. The result is n divided by the quantity n minus 2.

Complex Rational Expressions

Complex fractions are fractions in which the numerator or denominator contains a fraction. We previously simplified complex fractions like these:

\displaystyle \frac{\frac{3}{4}}{\frac{5}{8}} \qquad\qquad \frac{\frac{x}{2}}{\frac{xy}{6}}

A complex rational expression is a rational expression in which the numerator and/or the denominator contains a rational expression.

 
Examples
\displaystyle\frac{\frac{4} {y-3}}{\frac{8} {y^2 -9}} \displaystyle\frac{\frac{1}{x} + \frac{1}{y}} {\frac{x}{y} - \frac{y}{x}}} \displaystyle\frac{\frac{2} {x+6}}{\frac{4} {x-6} - \frac{4}{x^2 - 36}}

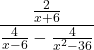We will use two methods to simplify complex rational expressions. The following is the first type:

For Example

\displaystyle\frac{\frac{6x^2 - 7x + 2} {4x - 8}}{\frac{2x^2 - 8x + 3} {x^2 - 5x + 6}}

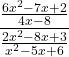
We noted that fraction bars tell us to divide, so rewrote it as the division problem:

\displaystyle(\frac{6x^2 -7x + 2} {4x - 8}) ÷ \displaystyle(\frac{2x^2 -8x + 3} {x^2 -5x + 6})

Then, we multiplied the first rational expression by the reciprocal of the second, just like we do when we divide two fractions.

Try it!

Simplify the complex rational expression by writing it as division: \displaystyle\frac{\frac{6} {x - 4}}{\frac{3} {x^2 - 16}}.

Solution

Solution (click to reveal)
Steps Algebraic
Original Problem \displaystyle\frac{\frac{6} {x - 4}}{\frac{3} {x^2 - 16}}
Rewrite the complex fraction as division.  \displaystyle\frac{6} {x - 4} ÷ \displaystyle\frac{3} {x^2 - 16}
Rewrite as the product of first times the reciprocal of the second. \displaystyle\frac{6} {x - 4} \cdot \displaystyle\frac{x^2 - 16} {3}
Factor.  \displaystyle\frac{3 \cdot 2} {x-4} \cdot \displaystyle\frac{(x - 4)(x + 4)} {3}
Multiply.  \displaystyle\frac {3 \cdot 2(x - 4)(x + 4)}{3(x - 4)}
Remove common factors.  \boldsymbol{\displaystyle\frac { \Ccancel[myred1]{3} \cdot 2 \Ccancel[myred1]{(x - 4)} (x + 4)}{\Ccancel[myred1]{3}\Ccancel[myred1]{(x - 4 )}}}
Simplify.  2(x + 4)

Are there any value(s) of x that should not be allowed? The original complex rational expression had denominators of x − 4 and x2 − 16. This expression would be undefined if x = 4 or x = −4.

 

Method 1:

Steps to simplify Complex Rational Expressions as Division:

  1. Simplify the numerator and denominator.
  2. Rewrite the complex rational expression as a division problem.
  3. Divide the expressions.

Try it!

Simplify the complex rational expression by writing it as division: 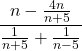\displaystyle\frac{n-\frac{4n} {n + 5}}{\frac{1} {n + 5}+\frac{1}{n - 5}}.

Solution

Solution (click to reveal)
Steps Algebraic
Example 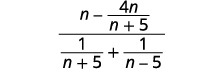Simplify the complex rational expression n minus the quantity 4 n divided by the quantity n plus 5 all divided by the sum of 1 divided by the quantity n plus 5 and 1 divided by the quantity n minus 5.
Simplify the numerator and denominator.
Find common denominators for the numerator and
denominator.		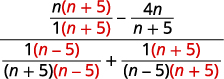 Simplify the numerator 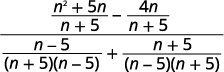and denominator. Find the common denominators for the numerator and denominator. The result is the n times the quantity n plus 5 all divided by 1 times the quantity n plus 5 minus the quantity 4 n divided by the quantity n plus 5 all divided by 1 times the quantity n minus 5 divided by the quantity n plus 5 times the quantity n minus 5 plus the quantity 1 times the quantity n plus 5 divided by the quantity n plus 5 times the quantity n minus 5.
Simplify the numerators. Simplify the numerators. The result is the quantity n squared plus 5 n divided by the quantity n plus 5 minus the quantity 4 n divided by the quantity n plus 5 all divided by 1 times the quantity n minus 5 divided by the quantity n plus 5 times the quantity n minus 5 plus 1 times the quantity n plus 5 divided by the quantity n plus 5 times the quantity n minus 5.
Subtract the rational expressions in the numerator and
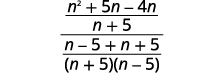add in the denominator.		 Subtract the rational expressions in the numerator and add in the denominator. The result is the quantity n squared plus 5 n minus 4 n divided by the quantity n plus 5 all divided by the quantity n minus 5 plus n plus 5 divided by the quantity n plus 5 times the quantity n minus 5.
Simplify. (We now have one rational expression over
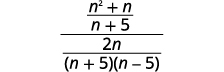one rational expression.)		 Simplify. We now have one rational expression over one rational expression. The result is the quantity n squared plus n divided by the quantity n plus 5 all divided by the quantity 2 n divided by the quantity n plus 5 times the quantity n minus 5.
Rewrite as fraction division. Rewrite the expression as fraction division. The result is the quotient of the quantity n squared plus n divided by the quantity n plus 5 and the quantity 2 n divided by the quantity n plus 5 times the quantity n minus 5.
Multiply the first times the reciprocal of the second. Multiply the first fraction times the reciprocal of the second fraction. The result is the quantity n squared plus n divided by the quantity n plus 5 times the quantity of n plus 5 times the quantity n minus 5 all divided by the quantity 2 n.
Factor any expressions if possible. Factor any expressions if possible. The result us n times the quantity n plus 1 times the quantity n plus 5 times the quantity n minus 5 all divided by the product of the quantity n plus 5 and 2 n.
Remove common factors. Remove the common factors, n and n plus 5, from the numerator and denominator.
Simplify. Simplify. The result is the product of the quantity n plus 1 and the quantity n minus 5 all divided by 2.

 

As we did earlier with rationals that have unlike denominators, we can use that strategy here to simplify complex rational expressions as well. We will multiply the numerator and denominator by the LCD of all the rational expressions.

Method 2:

Simplify Complex Rationals by LCD

  1. Find the LCD of all fractions in the complex rational expression.
  2. Multiply the numerator and denominator by the LCD.
  3. Simplify the expression.

Try it!

Simplify the complex rational expression by using the LCD: 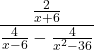\displaystyle\frac{\frac{2} {x + 6}}{\frac{4} {x - 6}-\frac{4}{x^2 - 36}}.

Solution

Solution (click to reveal)
Steps Algebraic
Example 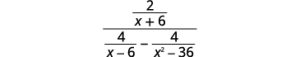Simplify the complex rational expression, 2 divided by the quantity x plus 6 all divided by the difference between 4 divided by the quantity x minus 6 and 4 divided by the quantity x squared minus 36.
Find the LCD of all fractions in the complex rational
expression.		 The LCD is x2 − 36 = (x + 6) (x − 6).
Multiply the numerator and denominator by the LCD. 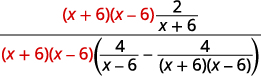Multiply the numerator and denominator by the least common denominator. The result is the quantity x plus 6 times the quantity x minus 6 times the quantity 2 divided by the quantity x plus 6 all divided by the quantity x plus 6 times the quantity x minus 6 times the difference between the quantity 4 divided by the quantity x minus 6 and 4 divided by the product of the quantity x plus 6 and the quantity x minus 6.
Simplify the expression.
Distribute in the denominator. 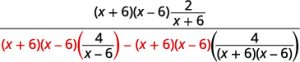Distribute, the quantity x plus 6 and x minus 6, in the denominator. The result is the quantity x plus 6 times the quantity x minus 6 times the quantity 2 divided by the quantity x plus 6 all divided by the quantity x plus 6 times the quantity x minus 6 times the quantity 4 divided by the quantity x minus 6 minus the quantity x plus 6 times the quantity x minus 6 times 4 divided by the product of the quantity x plus 6 and the quantity x minus 6.
Simplify. Simplify by removing the common factors, x plus 6 from the numerator, and the quantity x minus 6 times the quantity x plus 6, from the denominator. The result is 2 times the quantity x minus 6 all divided by the product of 4 and the quantity x plus 6 minus 4.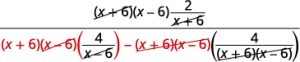
Simplify. To simplify the denominator, distribute and combine like terms. The result is 2 times the quantity x minus 6 all divided by the quantity 4 x plus 20.
To simplify the denominator, distribute
and combine like terms.		 To simplify the denominator, distribute and combine like terms. The result is 2 times the quantity x minus 6 all divided by the quantity 4 x plus 20.
Factor the denominator. Factor the denominator. The result is 2 times the quantity x minus 6 all divided by 4 times the quantity x plus 5.
Remove common factors. Notice that 4 in the denominator is 2 times 2. Remove the common factor, 2, from the numerator and denominator shown as 2 times the quantity x minus 6 all divided by 2 times two, times the quantity x plus 5.
Simplify. The result is the quantity x minus 6 all divided by 2 times the quantity x plus 5. Notice that there are no more factors common to the numerator and denominator.
Notice that there are no more factors
common to the numerator and denominator.

 

Try it!

Simplify the complex rational expression by using the LCD: 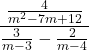\displaystyle\frac{\frac{4} {m^2 - 7m + 12}}{\frac{3} {m - 3}-\frac{2}{m - 4}}

Solution

Solution (click to reveal)
Steps Algebraic
Example Simplify the complex rational expression, 4 divided by the quantity m squared minus 7 m plus 12 all divided by the difference between 3 divided by the quantity m minus 3 and 2 divided by the quantity m minus 4.
Find the LCD of all fractions in the
complex rational expression.		 The LCD is (m −  3)(m − 4).
Multiply the numerator and
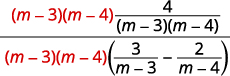denominator by the LCD.		 Multiply the numerator and denominator by the least common denominator. The result is the quantity m minus 3 times the quantity m minus 4 times the quantity 4 divided by the quantity m minus 3 times the quantity m minus 4 all divided by the quantity m minus 3 times the quantity m minus 4 times the difference between 3 divided by the quantity m minus 3 and 2 divided by the quantity m minus 4.
Simplify. Simplify by removing the common factors, m minus 3 and m minus 4, from the numerator and denominator. Shown as the quantity m minus 3 times the quantity m minus 4 [both are shown crossed through] times the quantity 4 divided by the quantity m minus 3 times the quantity m minus 4 [shown crossed through] all divided by the quantity m minus 3 [also crossed out] times the quantity m minus 4 times the difference between 3 divided by the quantity m minus 3 [also struck through] minus the quantity m minus 3 times the quantity m minus 4 [which is sstruck through] times the difference between 2 divided by the quantity m minus 4 [also struck through].
Simplify. The result is 4 divided by the product of 3 and m minus 4 minus the product of 2 and minus 3.
Distribute. Distribute the factors 3 and 2 in the denominator. The result is 4 divided by the quantity 3 m minus 12 minus 2 m plus 6.
Combine like terms. Combine like terms in the denominator. The result is 4 divided by the quantity m minus 6

 

Key Concepts

  • Determine the values for which a rational expression is undefined.
    1. Set the denominator equal to zero.
    2. Solve the equation.
  • Equivalent Fractions Property

    If a, b, and c are numbers where b ≠ 0, c ≠ 0, then 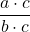\displaystyle\frac{a}{b} = \displaystyle\frac{a\cdot c}{b\cdot c} and \displaystyle\frac{a\cdot c}{b\cdot c} = \frac{a}{b}.
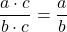  • How to simplify a rational expression.
    1. Factor the numerator and denominator completely.
    2. Simplify by dividing out common factors.
  • Opposites in a Rational Expression

    The opposite of a − b is b −  a.

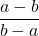    \displaystyle\frac{a - b} {b - a} = -1  a ≠ b

    An expression and its opposite divide to −1.

  • Multiplication of Rational Expressions

    If p, q, r, and s are polynomials where q ≠ 0, s ≠ 0, then

    \displaystyle\frac{p}{q} \boldsymbol{\cdot} \frac{r}{s} = \frac{pr}{qs}

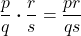
  • How to multiply rational expressions.
    1. Factor each numerator and denominator completely.
    2. Multiply the numerators and denominators.
    3. Simplify by dividing out common factors.
  • Division of Rational Expressions

    If p, q, r, and s are polynomials where q ≠ 0, r ≠ 0, s ≠ 0, then

    \displaystyle\frac{p}{q} \boldsymbol{\div} \frac{r}{s} = \frac{p}{q}\boldsymbol{\cdot}\frac{s}{r}

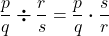
  • How to divide rational expressions.
    1. Rewrite the division as the product of the first rational expression and the reciprocal of the second.
    2. Factor the numerators and denominators completely.
    3. Multiply the numerators and denominators together.
    4. Simplify by dividing out common factors.

 

  1. Rational Expressions chapter derived from Openstax Intermediate algebra, Rational Expressions and Functions, Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book