"

10 Other Types of Equations

Topics Covered:

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
  1. Solve Polynomial Equations
  2. Solve Equations in the Quadratic Form with Substitution
  3. Absolute Value Equations
  4. Key Concepts

Solving Polynomial Equations by Factoring

We have already solved polynomial equations of degree one. Polynomial equations of degree one are linear equations and are of the form ax + b = c.

We have now also solved polynomial equations of degree two. A polynomial equation of degree two is called a quadratic equation.

But what about those equations with a degree of 3 or higher? Some of them we will be able to solve by Factoring.

Try it! – Solve a Polynomial by Grouping

Solve by grouping: x3 + x2 − 9x − 9 = 0.

Solution:

This polynomial consists of 4 terms, which we can solve by grouping. Grouping procedures require factoring the first two terms and then factoring the last two terms. If the factors in the parentheses are identical, we can continue the process and solve, unless more factoring is suggested.

Algebraic
x3 + x2 − 9x − 9 = 0
x2(x + 1) − 9(x + 1) = 0
(x2 − 9)(x + 1) = 0

The grouping process ends here, as we can factor x2 − 9 using the difference of squares formula.

Algebraic
(x2 − 9)(x + 1) = 0   
(x − 3)(x + 3)(x + 1) = 0
x = 3
x = −3
x = −1

The solutions are 3,−3, and −1. Note that the highest exponent is 3 and we obtained 3 solutions.

Analysis

We looked at solving quadratic equations by factoring when the leading coefficient is 1. When the leading coefficient is not 1, we solved by grouping. Grouping requires four terms, which we obtained by splitting the linear term of quadratic equations. We can also use grouping for some polynomials of degree higher than 2, as we saw here, since there were already four terms.

Solve Equations in the Quadratic Form

Sometimes when we factored trinomials, the trinomial did not appear to be in the ax2 + bx + c form. So we factored by substitution allowing us to make it fit the ax2 + bx + c form. We used the standard u for the substitution.

To factor the expression x4 − 4x2 − 5, we noticed the variable part of the middle term is x2 and its square, x4, is the variable part of the first term. (We know (x2)2 = x4.) So we let u = x2 and factored.

Steps Algebraic
Equation Start with the expression x to the fourth power minus 4 x squared minus 5.
Let u = x2 and substitute. Rewrite the expression as the square of x squared minus 4 times x squared minus 5.
Simplify Let u equal x squared and substitute u into the expression to yield u squared minus 4 u minus 5.
Factor the trinomial. Factor the trinomial as the product of u plus 1 and u minus 5.
Replace u with x2. Replace u with x squared to get the product of x squared plus 1 and x squared minus 5.
Quadratic Form

If the exponent on the middle term is one-half of the exponent on the leading term, we have an equation in quadratic form, which we can solve as if it were a quadratic. We substitute a variable for the middle term to solve equations in quadratic form.

How to solve an equation in quadratic form.

  1. Identify the exponent on the leading term and determine whether it is double the exponent on the middle term.
  2. If it is, substitute a variable, such as u, for the variable portion of the middle term.
  3. Rewrite the equation so that it takes on the standard form of a quadratic.
  4. Solve using one of the usual methods for solving a quadratic.
  5. Replace the substitution variable with the original term.
  6. Solve the remaining equation.

Similarly, sometimes an equation is not in the ax2 + bx + c = 0 form but looks much like a quadratic equation. Then, we can often make a thoughtful substitution that will allow us to make it fit the ax2 + bx + c = 0 form. If we can make it fit the form, we can then use all of our methods to solve quadratic equations.

Notice that in the quadratic equation ax2 + bx + c = 0, the middle term has a variable, x, and its square, x2, is the variable part of the first term. Look for this relationship as you try to find a substitution.

The next example shows the steps for solving an equation in quadratic form.

Try it! – How to Solve Equations in Quadratic Form

Solve: 6x4 − 7x2 + 2 = 0

Solution:


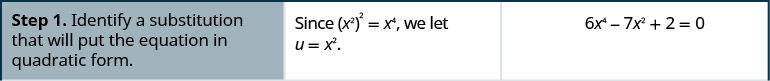
Step 1 is to identify a substitution that will put the equation in quadratic form. Look at the equation 6 x to the fourth power minus 7 x squared plus 2 equals 0. Since the square of x squared equals x to the fourth, let u equals x squared.Step 2 is to rewrite the equation with the substitution to put it in quadratic form. Rewrite the equation to prepare for the substitution to show 6 times the square of x squared minus 7 times x squared plus 2 equals 0. Substitute u equals x squared to get the new equation 6 times u squared minus 7 u plus 2 equals 0.Step 3 is to solve the quadratic equation for u. We can solve by factoring, so rewrite the equation as the product of 2 u minus 1 and 3 u minus 2 equals 0. Use the Zero Product Property to create 2 equations. If 2 u minus 1 equals 0, then 2u equals one, so u equals one half. If 3 u minus 2 equals 0, then 3 u equals 2 and u equals two thirds.In step 4, substitute the original variable back into the results. In this case replace u with x squared. So u equals one half becomes x squared equals one half and u equals two thirds becomes x squared equals two thirds.

In the next example, the binomial in the middle term, (x − 2) is squared in the first term. If we let u = x − 2 and substitute, our trinomial will be in ax2 + bx + c form.

Try it!

Solve: (x − 2)2 + 7(x − 2) + 12 = 0.

Solution:

Steps Algebraic
Equation Write the equation. The square of x minus 2 plus 7 times the expression x minus 2 plus 12 equals zero.
Prepare for the substitution. Prepare for the substitution by viewing x − 2 as a variable. These are marked in red in the previous equation
Let u = x − 2 and substitute. Let u equal x minus 2 and substitute. The equation becomes u squared plus 7 u plus 12 equals 0.
Solve by factoring. Factor the expression on the left side of the equation. The product of u plus 3 and u plus 4 equals 0.By the Zero Product Property, u plus 3 equals 0 or u plus 4 equals 0.So u equals negative 3 or u equals negative 4.
Replace u with x − 2. Replace u with x minus 2 and solve for x. If u equals negative 3, then x minus 2 equals negative 3 and x equals negative 1. If u equals negative 4, then x minus 2 equals negative 4 and x equals negative 2.
Solve for x. Replace u with x minus 2 and solve for x. If u equals negative 3, then x minus 2 equals negative 3 and x equals negative 1. If u equals negative 4, then x minus 2 equals negative 4 and x equals negative 2.
Check:

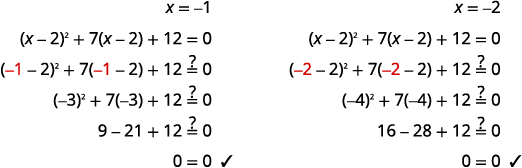 Check the solutions. Start with x equals negative one. Substitute negative one for x in the left-hand side of the original equation to get square of negative one minus two plus seven times the expression negative one minus two plus twelve. We need to show that this expression equals zero. Simplify to yield the square of negative three plus seven times negative three plus twelve, or nine minus twenty-one plus twelve which equals zero. X equals negative one is a solution. Next, check x equals negative two. Substitute negative two for x in the left-hand side of the original equation to get square of negative two minus two plus seven times the expression negative two minus two plus twelve. We need to show that this expression equals zero. Simplify to yield the square of negative four plus seven times negative four plus twelve, or sixteen minus twenty-eight plus twelve which equals zero. X equals negative two is a solution.

In the next example, we notice that (\sqrt{x})2 = x.  Also, remember that when we square both sides of an equation, we may introduce extraneous roots. Be sure to check your answers!

Try it!

Solve: \displaystyle x-3\sqrt{x}+2=0.

Solution:

The \displaystyle\sqrt{x} in the middle term, is squared in the first term \displaystyle\left(\sqrt{x}\right)^{2}=x. If we let \displaystyle u=\sqrt{x} and substitute, our trinomial will be in ax2 + bx + c = 0 form.

Steps Algebraic
Equation Write the equation. The x minus 3 times the square root of x plus 2 equals zero.
Rewrite the trinomial to prepare for the substitution. Rewrite the x as the square of square root x to prepare for the substitution. THe square root from the original equaiotn are highlighted red.
Let \displaystyle u=\sqrt{x} and substitute. Let u equal square root x and substitute. The equation becomes u squared minus 3 u plus 2 equals 0.
Solve by factoring. Factor the expression on the left side of the equation. The product of u minus 3 and u minus 1 equals 0.By the Zero Product Property, u minus 2 equals 0 or u minus 1 equals 0.So u equals 1 or u equals 1.
Replace u with \displaystyle\sqrt{x}. Replace u with square root x and solve for x by squaring both sides. If u equals 2, then square root x equals 2 and x equals 4. If u equals 1, then square root x equals 1 and x equals 1.
Solve for x, by squaring both sides. Replace u with square root x and solve for x by squaring both sides. If u equals 2, then square root x equals 2 and x equals 4. If u equals 1, then square root x equals 1 and x equals 1.
Check:

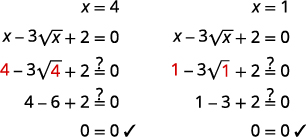 Check the solutions. Start with x equals 4. Substitute 4 for x in the left-hand side of the original equation to get 4 minus 3 times square root 4 plus 2. We need to show that this expression equals zero. Simplify to yield 4 minus 6 plus 2 which equals zero. X equals 4 is a solution. Next, check x equals 1. Substitute 1 for x in the left-hand side of the original equation to get 1 minus 3 times square root 1 plus 2. We need to show that this expression equals zero. Simplify to yield 1 minus 3 plus 2 which equals zero. X equals 1 is a solution.

Substitutions for rational exponents can also help us solve an equation in quadratic form. Think of the properties of exponents as you begin the next example.

Try it!

  1. Solve: \displaystyle x^{\frac{2}{3}}-2x ^{\frac{1}{3}}-24=0.

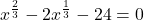Solution:

The \displaystyle x^{\frac{1}{3}} in the middle term is squared in the first term \displaystyle\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}. If we let \displaystyle u=x^{\frac{1}{3}} and substitute, our trinomial will be in ax2 + bx + c = 0 form.

Steps Algebraic
Equation Write the equation. X to the two-thirds power minus 2 times x to the one-third power minus 24 equals zero.
Rewrite the trinomial to prepare for the substitution. Rewrite x to the two-thirds power as the square of x to the one-third power to prepare for the substitution.
Let u = x^\frac{1}{3} and substitute. Let u equal the one-third power of x and substitute. The equation becomes u squared minus 2 u minus 24 equals 0.
Solve by factoring. Factor the expression on the left side of the equation. The product of u minus 6 and u plus 4 equals 0.By the Zero Product Property, u minus 6 equals 0 or u plus 4 equals 0. So u equals 6 or u equals negative 4.By the Zero Product Property, u minus 6 equals 0 or u plus 4 equals 0. So u equals 6 or u equals negative 4.
Replace u with x^\frac{1}{3} . Replace u with x to the one-third power and solve for x by cubing both sides. If u equals 6, then x to the one-third power equals 6, If u equals negative 4, then x to the one-third power equals negative 4,
Solve for x by cubing both sides. Replace u with x to the one-third power and solve for x by cubing both sides. So x equals 6 cubed, or 216. So x equals the cube of negative 4, or negative 64.Replace u with x to the one-third power and solve for x by cubing both sides. So x equals 6 cubed, or 216. So x equals the cube of negative 4, or negative 64.
Check:

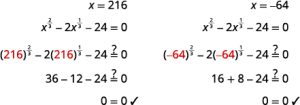 Check the solutions. Start with x equals 216. Substitute 216 for x in the left-hand side of the original equation to get 216 to the two-thirds power minus 2 times 216 to the one-third power minus 24. We need to show that this expression equals zero. Simplify to yield 36 minus 12 minus 24 which equals zero. X equals 216 is a solution. Next, check x equals negative 64. Substitute negative 64 for x in the left-hand side of the original equation to get negative 4 to the two-thirds power minus 2 times negative 4 to the one-third power minus 24. We need to show that this expression equals zero. Simplify to yield 16 plus 8 minus 24 which equals zero. X equals negative 64 is a solution.

2. Solve: \displaystyle x^{\frac{2}{3}}-5x^{\frac{1}{3}}-14=0.

Solution:

\displaystyle x=-8, \displaystyle x=343

In the next example, we need to keep in mind the definition of a negative exponent as well as the properties of exponents.

Tip

If n is an integer and a ≠ 0, then \displaystyle a^{-n}=\frac{1}{a^{n}} or \displaystyle\frac{1}{a^{-n}}=a^{n}.

 

Try it!

Solve: \displaystyle 3x^{-2}-7x^{-1}+2=0.

Solution:

The \displaystyle x^{-1} in the middle term is squared in the first term \displaystyle\left(x^{-1}\right)^{2}=x^{-2}. If we let \displaystyle u=x^{-1} and substitute, our trinomial will be in ax2 + bx + c = 0 form.

Steps Algebraic
Equation Write the equation. Three times x to the negative two power minus 7 times x to the negative one power plus 2 equals zero.
Rewrite the trinomial to prepare for the substitution. Rewrite x to the negative two power as the square of x to the negative one power to prepare for the substitution.
Let \displaystyle u=x^{-1} and substitute. Let u equal the x to the negative one power and substitute. The equation becomes 3 u squared minus 7 u plus 2 equals 0.
Solve by factoring. Factor the expression on the left side of the equation. The product of 3 u minus 1 and u minus 2 equals 0.
By the Zero Product Property, 3 u minus 1 equals 0 or u minus 2 equals 0.
So u equals one third or u equals 2.
Replace u with \displaystyle x^{-1}. Replace u with x to the negative one power: then x to the negative one power equals one third,. and x to the negative one power equals 2,
Solve for x by taking the reciprocal since \displaystyle x^{-1}=\frac{1}{x}. If u equals one third, then x to the negative one power equals one third, so x equals 3. If u equals 2, then x to the negative one power equals 2, so x equals one half.
Check:
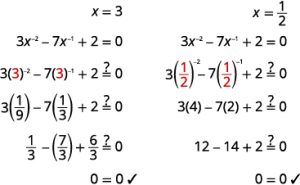Check the solutions. Start with x equals 3. Substitute 3 for x in the left-hand side of the original equation to get 3 times 3 to the negative 2 power minus 7 times 3 to the negative one power plus 2. We need to show that this expression equals zero. Simplify to yield 3 times one ninth minus 7 times one third plus 2 which equals one third minus seven thirds plus six thirds, or 0. X equals 3 is a solution. Next, check x equals one half. Substitute one half for x in the left-hand side of the original equation to get 3 times one half to the negative 2 power minus 7 times one half to the negative one power plus 2. We need to show that this expression equals zero. Simplify to yield 3 times 4 minus 7 times 2 plus 2 which equals 12 minus 14 plus 2, or 0. X equals one half is a solution.

Access this online resource for additional instruction and practice with solving quadratic equations.

 

Absolute Value Equations

As we prepare to solve absolute value equations, we review our definition of absolute value.

Absolute Value

The absolute value of a number is its distance from zero on the number line.

The absolute value of a number n is written as |n| and |n| ≥ 0 for all numbers.

Absolute values are always greater than or equal to zero.

We learned that both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value. For example:

−5 is 5 units away from 0, so |−5| = 5.  

5 is 5 units away from 0, so |5| = 5.

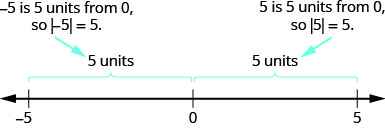
The figure is a number line with tick marks at negative 5, 0, and 5. The distance between negative 5 and 0 is given as 5 units, so the absolute value of negative 5 is 5. The distance between 5 and 0 is 5 units, so the absolute value of 5 is 5.
The numbers 5 and −5 are both five units away from zero.

For the equation |x| = 5, we are looking for all numbers that make this a true statement. We are looking for the numbers whose distance from zero is 5. We just saw that both 5 and -5 are five units from zero on the number line. They are the solutions to the equation.

If |x| = 5

then x = −5 or x = 5.

The solution can be simplified to a single statement by writing x = ±5. This is read, “x is equal to positive or negative 5”.

We can generalize this to the following property for absolute value equations.

Absolute Value Equations

For any algebraic expression, u, and any positive real number, a,

if |u| = a

then u = −a or u = a

Remember that an absolute value cannot be a negative number.

Try it!

Solve: ⓐ |x| = 8     ⓑ |y| = −6     ⓒ |z| = 0

Solution:

ⓐ

Steps Algebraic
Equation |x| = 8
Write the equivalent equations. x = −8 or x = 8
x = ±8

ⓑ

Steps Algebraic
Equation |y| = −6
No solution
Since an absolute value is always positive, there are no solutions to this equation.

ⓒ

Steps Algebraic
Equation |z| = 0
Write the equivalent equations. z = −0 or z = 0
Since −0 = 0,  z = 0
Both equations tell us that z = 0 and so there is only one solution.

To solve an absolute value equation, we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations.

How to solve absolute value equations.
  1. Isolate the absolute value expression.
  2. Write the equivalent equations.
  3. Solve each equation.
  4. Check each solution.

Try it! – How to Solve Absolute Value Equations

  1. Solve: |5x − 4| − 3 = 8.

Solution:


Step 1 is to isolate the absolute value expression. The difference between the absolute value of the quantity 5 x minus 4 and 3 is equal to 8. Add 3 to both sides. The result is the absolute value of the quantity 5 x minus 4 is equal to 11.Step 2 is to write the equivalent equations, 5 x minus 4 is equal to negative 11 and 5 x minus 4 is equal to 11.Step 3 is to solve each equation. Add 4 to each side. 5 x is equal to negative 7 or 5 x is equal to 15. Divide each side by 5. The result is x is equal to negative seven-fifths or x is equal to 3.Step 4 is to check each solution. Substitute 3 and negative seven-fifths into the original equation, the difference between the absolute value of the quantity 5 x minus 4 and 3 is equal to 8. Substitute 3 for x. Is the difference between the absolute value of the quantity 5 times 3 minus 4 and 3 equal to 8? Is the difference between the absolute value of the quantity 15 minus 4 and 3 equal to 8? Is the difference between the absolute value of the 11 and 3 equal to 8? Is 11 minus 3 equal to 8? 8 is equal to 8, so the solution x is equal to 3 checks. Substitute negative seven-fifths for x. Is the difference between the absolute value of the quantity 5 times negative seven-fifths minus 4 and 3 equal to 8? Is the difference between the absolute value of the quantity negative 7 minus 4 and 3 equal to 8? Is the difference between the absolute value of the negative 11 and 3 equal to 8? Is 11 minus 3 equal to 8? 8 is equal to 8, so the solution x is equal to negative seven-fifths checks.

2. Solve: 2|x − 7| + 5 = 9.

Solution:

Steps Algebraic
Equation 2|x − 7| + 5 = 9
Isolate the absolute value expression. 2|x − 7| = 4
Simplify |x − 7| = 2
Write the equivalent equations. x − 7 = −2 or x − 7 = 2
Solve each equation. x = 5 or x = 9
Check: Check using the original equation, the sum of 2 times the absolute value of the quantity x minus 7 and 5 is equal to 9. Is the sum of 2 times the absolute value of the quantity 5 minus 7 and 5 equal to 9? Is the sum of 2 times the absolute value of negative 2 and 5 equal to 9? Is 2 times 2 plus 5 equal to 9? Is 4 plus 5 equal to 9? 9 is equal to 9, so the solution x is equal to 5 checks. Is the sum of 2 times the absolute value of the quantity 9 minus 7 and 5 equal to 9? Is the sum of 2 times the absolute value of 2 and 5 equal to 9? Is 2 times 2 plus 5 equal to 9? Is 4 plus 5 equal to 9? 9 is equal to 9, so the solution x is equal to 9 checks.

3. Solve: \displaystyle\left|\frac{5}{6}x+3\right|+8=6.

Solution:

No solution

Key Concepts

  • Binomial Squares

    (a + b)2 = a2 + 2ab + b2
    (a − b)2 = a2 − 2ab + b2
  • Absolute Value Equations
    For any algebraic expression, u, and any positive real number, a,

if |u| = a

then u = −a or u = a

Remember that an absolute value cannot be a negative number.

  • How to Solve Absolute Value Equations
    1. Isolate the absolute value expression.
    2. Write the equivalent equations.
    3. Solve each equation.
    4. Check each solution.
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book