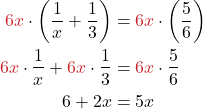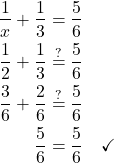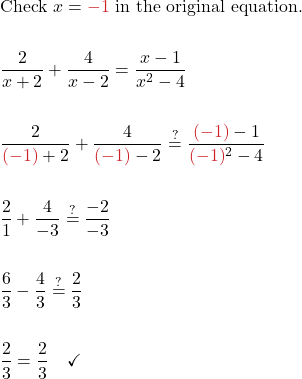Rational Equations & Functions

Elizabeth Pople

29 Rational Equations & Functions

Topics Covered:^[1]

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

Solve Rational Equations

After defining the terms ‘expression’ and ‘equation’ earlier, we have used them throughout this book. We have simplified many kinds of expressions and solved many kinds of equations.

A rational equation is an equation that contains at least one rational expression where the variable appears in at least one of the denominators.

You must make sure to know the difference between rational expressions and rational equations. The equation contains an equal sign.

Rational Expression Examples

Rational Equation Examples

$\displaystyle\frac{1}{8}x + \frac{1}{2}$

$\displaystyle\frac{1}{8}x + \frac{1}{2} = \frac{1}{4}$

$\displaystyle\frac{y + 6}{y^{2} - 36}$

$\displaystyle\frac{y + 6}{y^{2} - 36} = y + 1$

$\displaystyle\frac{1}{n - 3} + \frac{1}{n+4}$

$\displaystyle\frac{1}{n - 3} + \frac{1}{n + 4} = \frac{15}{n^{2} + n - 12}$

We have already solved linear equations that contained fractions. We found the LCD of all the fractions in the equation and then multiplied both sides of the equation by the LCD to “clear” the fractions.

However, since the original equation may have a variable in a denominator, we must be careful that we don’t end up with a solution that would make a denominator equal to zero. So before we begin solving a rational equation, we examine it first to find the values that would make any denominators zero. That way, when we solve a rational equation we will know if there are any algebraic solutions we must discard.

An algebraic solution to a rational equation that would cause any of the rational expressions to be undefined is called an extraneous solution to a rational equation.

Extraneous Solution to a Rational Equation

An extraneous solution to a rational equation is an algebraic solution that would cause any of the expressions in the original equation to be undefined.

We note any possible extraneous solutions, c, by writing x≠c next to the equation.

How to solve a rational equation

Note any value of the variable that would make any denominator zero.
Find the least common denominator of all denominators in the equation.
Clear the fractions by multiplying both sides of the equation by the LCD.
Solve the resulting equation.
Check:
- If any values found in Step 1 are algebraic solutions, discard them.
- Check any remaining solutions in the original equation.

Try it!

Solve: $\displaystyle\frac{1}{x} + \frac{1}{3} = \frac{5}{6}$ .

Solution (click to reveal)

Steps

Algebraic

Step 1. Note any value of the variable that would make any denominator zero. If x – 0, then $\; \displaystyle\frac{1}{x}}$ is undefined.

So we’ll write $x \neq 0$ next to the equation

$\displaystyle{\frac{1}{x} + \frac{1}{3} = \frac{5}{6}}, x \neq 0$

Step 2. Find the least common denominator of all denominators in the equation: $\displaystyle\frac{1}{x}, \frac{1}{3}, \text {and}\frac{5}{6}$ .

The LCD is 6x.

Step 3. Cleat the fractions by multiplying both sides of the equation by the LCD: SoMultiply both sides of the equation by the LCD, 6x.

Use the Distributive Property.

Simplify – and notice, no more fractions!

$\begin{align*} {\color{myred1}6x} \cdot \left( \frac{1}{x} + \frac{1}{3} \right) &= {\color{myred1}6x} \cdot \left( \frac{5}{6} \right) \\ {\color{myred1}6x} \cdot \frac{1}{x} + {\color{myred1}6x} \cdot \frac{1}{3} &= {\color{myred1}6x} \cdot \frac{5}{6} \\ 6 + 2x &= 5x\end{align*}$

Step 4. Solve the resulting equation & Simplify.

$\begin{align*} 6&= 3x \\ 2 &= x \end{align*}$

Step 5. Check.

If any value found in Step 1 are algebraic solutions, discard them. We did not get 0 as an algebraic solution.
Check any remaining solutions in the original equation. We substitute x = 2 into the original equation.

$\begin{align*} \frac{1}{x} + \frac{1}{3} &= \frac{5}{6} \\ \frac{1}{2} + \frac{1}{3} &\stackrel{?}{=} \frac{5}{6} \\ \frac{3}{6} + \frac{2}{6} &\stackrel{?}{=} \frac{5}{6} \\ \frac{5}{6} &= \frac{5}{6} \quad \checkmark \end{align*}$

$\displaystyle {The \; solution \; is \; x = 2.}$

Solve: 1 – $\displaystyle\frac{5}{y} = −\frac{6}{y^{2}}$ .

Solution (click to reveal)

Steps

Algebraic

Equation

1 – $\displaystyle\frac{5}{y} = −\frac{6}{y^{2}}$

Note any value of the variable that would make
any denominator zero.

1 – $\displaystyle\frac{5}{y} = −\frac{6}{y^{2}}, y \neq 0$

Find the least common denominator of all denominators in
the equation.

The LCD is y².

Clear the fractions by multiplying both sides of
the equation by the LCD.

$\displaystyle y^{2}\left(1-\frac{5}{y}\right) = y^{2}\left(\frac{6}{y^{2}}\right)$

Distribute.

$\displaystyle y^{2}\cdot 1 - y^{2}\left(\frac{5}{y}\right) = y^{2}\left(\frac{6}{y^{2}}\right)$

Multiply.

$\displaystyle y^2 - 5y = -6$

Solve the resulting equation. First
write the quadratic equation in standard form.

$\displaystyle y^2 - 5y + 6 = 0$

Factor.

$\displaystyle (y - 2)(y - 3) = 0$

Use the Zero Product Property.

$\displaystyle (y - 2) = 0 \quad \text {or} \quad (y - 3) = 0$

Solve.

$\displaystyle y = 2 \quad \text {or} \quad y = 3$

Check.
We did not get 0 as an algebraic solution.

$\displaystyle {Check \; $ y = \textcolor{myred1}{2} $ and $ y = \textcolor{myblue1}{3} $ in the original equation.}$

$\begin{align*} 1 - \frac{5}{y} &= -\frac{6}{y^2} & \quad 1 - \frac{5}{y} &= -\frac{6}{y^2} \\ 1 - \frac{5}{\textcolor{myred1}{2}} &\stackrel{?}{=} -\frac{6}{\textcolor{myred1}{2}^2} & \quad 1 - \frac{5}{\textcolor{myblue1}{3}} &\stackrel{?}{=} -\frac{6}{\textcolor{myblue1}{3}^2} \\ 1 - \frac{5}{2} &\stackrel{?}{=} -\frac{6}{4} & \quad 1 - \frac{5}{3} &\stackrel{?}{=} -\frac{6}{9} \\ \frac{2}{2} - \frac{5}{2} &\stackrel{?}{=} -\frac{6}{4} & \quad \frac{3}{3} - \frac{5}{3} &\stackrel{?}{=} -\frac{6}{9} \\ -\frac{3}{2} &\stackrel{?}{=} -\frac{6}{4} & \quad -\frac{2}{3} &\stackrel{?}{=} -\frac{6}{9} \\ -\frac{3}{2} &= -\frac{3}{2} \quad \checkmark & \quad -\frac{2}{3} &= -\frac{2}{3} \quad \checkmark \end{align*}$

Solution

The solution is y = 2, y = 3.

A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as (x + 1). Always consider a binomial as an individual factor—the terms cannot be separated. For example, suppose a problem has three terms and the denominators are x, x − 1, and 3x − 3. First, factor all denominators. We then have x, (x − 1), and 3(x − 1) as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of (x − 1). The x in the first denominator is separate from the x in the (x − 1) denominators. An effective way to remember this is to write factored and binomial denominators in parentheses, and consider each parentheses as a separate unit or a separate factor. The LCD in this instance is found by multiplying together the x, one factor of (x − 1), and the 3. Thus, the LCD is the following:

x (x − 1) 3 = 3x (x − 1)

So, both sides of the equation would be multiplied by 3x(x − 1). Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out. Another example is a problem with two denominators, such as x and x² + 2x. Once the second denominator is factored as x² + 2x = x(x + 2), there is a common factor of x in both denominators and the LCD is x(x + 2).

In the next example, the last denominators is a difference of squares. Remember to factor it first to find the LCD.

Try it!

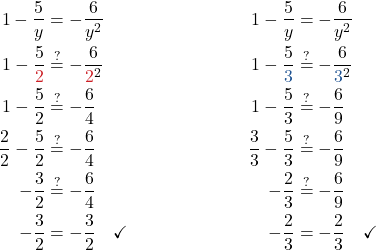
Solve: $\displaystyle\frac{2}{x+2}+\frac{4}{x-2}=\frac{x-1}{x^{2}-4}$ .

Solution (click to reveal)

Steps

Algebraic

Equation

$\displaystyle\frac{2}{x+2}+\frac{4}{x-2}=\frac{x-1}{x^{2}-4}$

Note any value of the variable that would make any denominator zero.

$\displaystyle\frac{2}{x+2}+\frac{4}{x-2}=\frac{x-1}{(x+2)(x-2)}$ , $\displaystyle x\neq -2$ , $\displaystyle x\neq 2$

Find the least common denominator of all denominators in the equation.

The LCD is (x + 2)(x − 2).

Clear the fractions by multiplying both sides of the equation by the LCD.

$\displaystyle \boldsymbol{ \textcolor{myred1}{(x + 2)(x - 2)} \left( \frac{2}{x+2} + \frac{4}{x-2} \right)}$ =

$\displaystyle \boldsymbol{\textcolor{myred1}{(x + 2)(x - 2)} \left( \frac{x - 1}{x^{2} - 4} \right)}$

Distribute.

$\displaystyle \boldsymbol{\textcolor{myred1}{(x + 2)(x - 2)} \cdot \frac{2}{x+2} + \textcolor{myred1}{(x + 2)(x - 2)} \cdot \frac{4}{x-2} =}$

$\displaystyle \boldsymbol{\left( \textcolor{myred1}{(x + 2)(x - 2)} \right) \cdot \left( \frac{x - 1}{x^{2} - 4} \right)}$

Remove common factors.

$\boldsymbol{{\color{myred1}\Ccancel{(x + 2)}(x - 2)}}$ $\boldsymbol{\displaystyle\frac{2}{\Ccancel{x+2}}}$ + $\boldsymbol{{\color{myred1}(x + 2)\Ccancel{(x - 2)}}}$ $\boldsymbol{\displaystyle\frac{4}{\Ccancel{x-2}}}$

= $\boldsymbol{{\color{myred1}\Ccancel{(x + 2)(x - 2)}}}$ $\boldsymbol{\displaystyle\left(\frac{x-1}{\Ccancel{x^{2}-4}}\right)}$

Simplify.

$\displaystyle \boldsymbol{2 \cdot \textcolor{myred1}{(x - 2)} + 4 \cdot \textcolor{myred1}{(x + 2)} = x - 1}$

Distribute.

$\displaystyle 2x - 4 + 4x + 8 = x - 1$

Solve.

$\displaystyle 6x + 4 = x - 1$

$\displaystyle 5x = -5$

$\displaystyle x = - 1$

Check:
We did not get 2 or −2 as algebraic solutions.

$\begin{align*} &\text{Check } x = \textcolor{myred1}{-1} \text{ in the original equation.} \\ \\ &\frac{2}{x + 2} + \frac{4}{x - 2} = \frac{x - 1}{x^2 - 4} \\ \\ &\frac{2}{\textcolor{myred1}{(-1)} + 2} + \frac{4}{\textcolor{myred1}{(-1)} - 2} \stackrel{?}{=} \frac{\textcolor{myred1}{(-1)} - 1}{\textcolor{myred1}{(-1)}^2 - 4} \\ \\ &\frac{2}{1} + \frac{4}{-3} \stackrel{?}{=} \frac{-2}{-3} \\ \\ &\frac{6}{3} - \frac{4}{3} \stackrel{?}{=} \frac{2}{3} \\ \\ &\frac{2}{3} = \frac{2}{3} \quad \checkmark \end{align*}$

Solution

The solution is x = −1.

In the next example, the first denominator is a trinomial. Remember to factor it first to find the LCD.

Try it!

Solve: $\displaystyle\frac{4}{3x^{2}-10x+3}+\frac{3}{3x^{2}+2x-1}=\frac{2}{x^{2}-2x-3}$ .

Solution (click to reveal)

Steps

Algebraic

Equation

$\displaystyle \frac{4}{(3x - 1)(x - 3)} + \frac{3}{(3x - 1)(x + 1)} = \frac{2}{(x - 3)(x + 1)}$

Factor all the denominators, so we can note any value of the variable that would make any denominator zero.

$\displaystyle \frac{4}{(3x - 1)(x - 3)} + \frac{3}{(3x - 1)(x + 1)} = \frac{2}{(x - 3)(x + 1)}$

x ≠ −1, x ≠ $\displaystyle\frac{1}{3}$ , x ≠ 3

Find the least common denominator.

The LCD is (3x − 1)(x + 1)(x − 3).

Clear the fractions by multiplying each side by the LCD.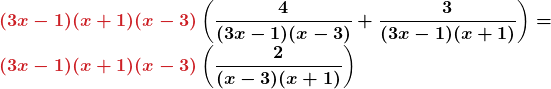

$\displaystyle \boldsymbol{ \textcolor{myred1}{(3x - 1)(x + 1)(x - 3)} \left( \frac{4}{(3x - 1)(x - 3)} + \frac{3}{(3x - 1)(x + 1)} \right) = }\newline \boldsymbol{\textcolor{myred1}{(3x - 1)(x + 1)(x - 3)} \left( \frac{2}{(x - 3)(x + 1)} \right)}$

Simplify

$\displaystyle 4{\color{myred1}(x + 1)} + 3{\color{myred1}(x - 3)} = 2{\color{myred1}(3x - 1)}$

Distribute.

$\displaystyle 4x + 4 + 3x - 9 = 6x - 2$

Simplify.

$\begin{align*} 7x -5 &= 6x -2 \\ x &= 3 \end{align*}$

Solution

The only algebraic solution was x = 3, but we said that x = 3 would make a denominator equal to zero. The algebraic solution is an extraneous solution.There is no solution to this equation.

Working with functions that are defined by rational expressions often lead to rational equations. Again, we use the same techniques to solve them.

Try it!

For rational function, $\displaystyle f(x)=\frac{2x-6}{x^2 - 8x+ 15}$ , a. find the domain of the function, b. solve f(x) = 1, and c. find the points on the graph at this function value.

Solution (click to reveal)

a. The domain of a rational function is all real numbers except those that make the rational expression undefined. So to find them, we will set the denominator equal to zero and solve.

Steps

Algebraic

Equation

$\displaystyle x^2 - 8x + 15 = 0$

Factor the trinomial.

$\displaystyle (x - 3)(x - 5) = 0$

Use the Zero Product Property.

$\displaystyle (x - 3) = 0 \; , \; (x - 5) = 0$

Solve.

$\displaystyle x = 3 \; , \; x = 5$

Solution

The domain is all real numbers except x ≠ 3, x ≠ 5.

b. f(x) = 1

Steps

Algebraic

Substitute in the rational expression.

$\displaystyle \frac{2x-6}{x^2 - 8x+ 15} = 1$

Factor the denominator.

$\displaystyle \frac{2x-6}{\left(x-3\right)\left(x-5\right)} = 1$

Multiply both sides by the LCD, (x−3)(x−5).

$\boldsymbol{\displaystyle {\color{myred1}\left(x-3\right)\left(x-5\right)}\frac{2x-6}{\left(x-3\right)\left(x-5\right)} = 1 {\color{myred1}\left(x-3\right)\left(x-5\right)}}$

Simplify.

$\displaystyle 2x - 6 = x^2 - 8x + 15$

Solve.

$\displaystyle 0 = x^2 - 10x + 21$

Factor.

$\displaystyle 0 = (x - 7)(x -3)$

Use the Zero Product Property.

$\displaystyle (x - 7) = 0 \; , \; (x -3) = 0$

Solve.

x = 7, x = 3

However, x = 3 is outside the domain of this function, so we discard that root as extraneous.

c. The value of the function is 1 when x = 7. So the points on the graph of this function when f(x) = 1 is (7,1).

Characteristics of Rational Functions

Similar to the equations we just looked at, a rational function is a function that can be written as the ratio (quotient) of two polynomial functions (meaning there are variables in the denominator). Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.

Rational Function

A rational function is a function that can be written as the ratio (quotient) of two polynomial functions P(x) and Q(x). Where Q(x)≠0,

f(x) = $\displaystyle \frac{P(x)}{Q(x)} = \frac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0}$

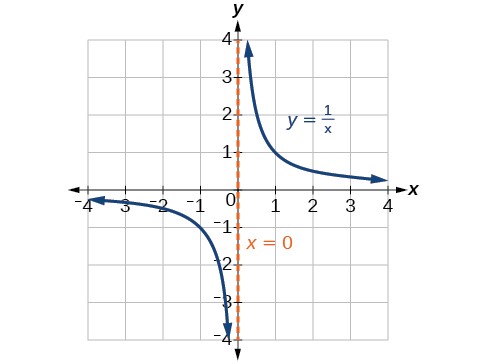
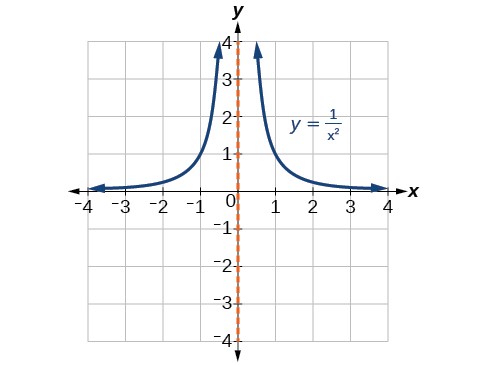
There are several key features of a Rational function that we can identify when looking at one in graphical form. Let’s begin by looking at the reciprocal (ie. Rational) toolkit function, f(x) = $\displaystyle \frac{1}{x}$ .
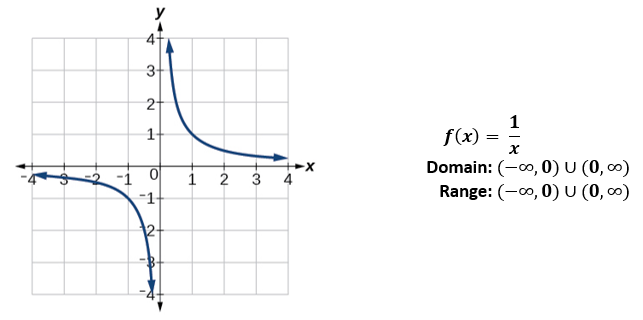
For the reciprocal function f(x)=1/x, we cannot divide by 0, so we must exclude 0 from the domain. Further, 1 divided by any value can never be 0, so the range also will not include 0. In set-builder notation, we could also write {x|x≠0}, the set of all real numbers that are not zero.

We cannot divide by zero, which means the function is undefined at x = 0; so zero is not in the domain (see image above). As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity).

x

–0.1

–0.01

–0.001

–0.0001

f(x) = $\displaystyle \frac{1}{x}$

–10

–100

–1000

–10,000

As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity).

x	0.1	0.01	0.001	0.0001
f(x) = $\displaystyle \frac{1}{x}$	10	100	1000	10,000

This behavior creates a vertical asymptote, which is a vertical line that the graph approaches but never crosses. In this case, the graph is approaching the vertical line x = 0 as the input becomes close to zero.

Vertical Asymptote

A vertical asymptote of a graph is a vertical line x = a where the graph tends toward positive or negative infinity as the input approaches a from either the left or the right.

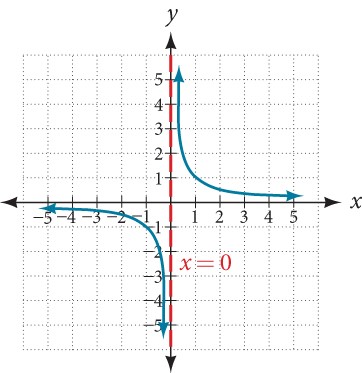
As the values of x approach infinity, the function values approach 0. As the values of x approach negative infinity, the function values approach 0. Based on this overall behavior and the graph, we can see that the function approaches 0 but never actually reaches 0; it seems to level off as the inputs become large. This behavior creates a horizontal asymptote, a horizontal line that the graph approaches as the input increases or decreases without bound. In this case, the graph is approaching the horizontal line y = 0.

Horizontal Asymptote

A horizontal asymptote of a graph is a horizontal line y=b where the graph approaches the line as the inputs increase or decrease without bound.

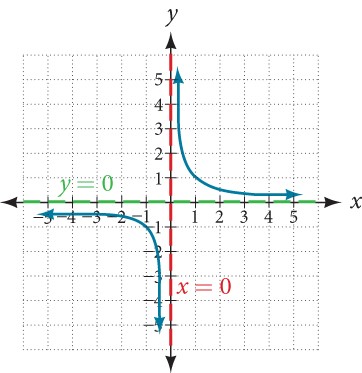
We will look more into how to identify both horizontal and vertical asymptotes below, but first try identifying them from a graph.

Try it!- Find the asymptotes from a Graph

Identify the vertical and horizontal asymptote in the following graph.

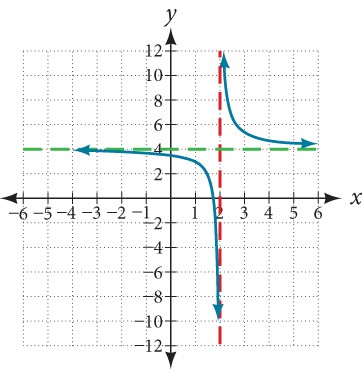
Graph of f(x)=1/(x-2)+4 with its vertical asymptote at x=2 and its horizontal asymptote at y=4.

Solution (click to reveal)

Notice that the graph is showing a vertical asymptote at x = 2, which tells us that the function is undefined at x = 2.

And as the inputs decrease without bound, the graph appears to be leveling off at output values of 4, indicating a horizontal asymptote at y = 4. As the inputs increase without bound, the graph levels off at 4.

Identifying Vertical Asymptotes, and Domain from an Equation

By looking at the graph of a rational function, we can easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location. We did this above by reading the graphs. Now we will look at how to identify them from the equation.

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

Given a rational function, identify any vertical asymptotes of its graph.

Factor the numerator and denominator.
Reduce the expression by canceling common factors in the numerator and the denominator. These common factors are restrictions in the domain where asymptotes do not occur called removable discontinuities, or “holes.”
With the simplified version, note any values that cause the denominator to be zero. These are where the vertical asymptotes occur.

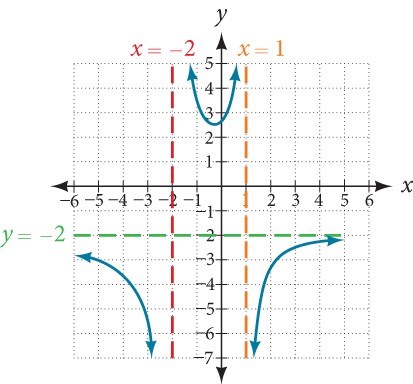
Try it! -Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of k(x) = $\displaystyle \frac{5+2x^2}{2-x-x^2}$ .

Solution (click to reveal)

First, factor the numerator and denominator.

k(x) = $\displaystyle \frac{5+2x^2}{2-x-x^2}$

$\displaystyle \frac{5+2x^2}{\left(2+x\right)\left(1-x\right)}$

There are no common factors between the numerator and denominator, so to find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

(2 + x) (1 − x) = 0

x = −2, 1

Neither x = –2 nor x = 1 are zeros of the numerator, so the two values indicate two vertical asymptotes.

Graph of k(x)=(5+2x)^2/(2-x-x^2) with its vertical asymptotes at x=-2 and x=1 and its horizontal asymptote at y=-2.

We already know a vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A reciprocal function cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.

Domain of a Rational Function

The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

How To: find the domain of Rational Functions

Set the denominator equal to zero.
Solve to find the x-values that cause the denominator to equal zero.
The domain is all real numbers except those found in Step 2.

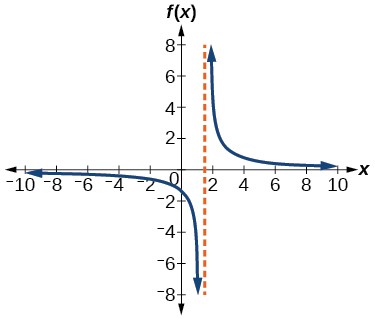
Try it! -Finding the Domain of a Rational Function

Find the domain of f(x) = $\displaystyle \frac{4}{2x-3}$

Solution (click to reveal)

Begin by setting the denominator equal to zero and solving.

2x-3 = 0

2x = 3

x = $\displaystyle \frac{3}{2}$

The denominator is equal to zero when x= $\displaystyle \frac{3}{2}$ . The domain of the function is all real numbers x ≠ $\displaystyle \frac{3}{2}$ .

Analysis

A graph of this function confirms that the function is not defined when x= $\displaystyle \frac{3}{2}$ . There is a vertical asymptote at x = $\displaystyle \frac{3}{2}$ .

Graph of f(x)=4/(2x-3) with its vertical asymptote at x=3/2.

Find the domain of f(x) = $\displaystyle \frac{x}{x^2+5x-36}$

Solution (click to reveal)

Begin by factoring the denominator and setting the factors equal to zero and solving.

x + 9 = 0 and x – 4 = 0

x = -9 and 4

The domain of the function is all real numbers x ≠ -9, 4.

At first glance, it appears that finding the domain and vertical asymptotes are the same process. While very similar, recall that factors common to both numerator and denominator are excluded when identifying the vertical asymptote. Take a look at the next example to see the difference.

Try it! – Domain & Vertical Asymptotes

Find the domain and vertical asymptotes of f(x) = $\displaystyle \frac{x+3}{x^2-9}$

Solution (click to reveal)

Begin by factoring the numerator and denominator.
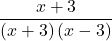
- Note that the numerator and denominator have a common factor of (x + 3). This will be important for the asymptote.
To find the domain begin by setting the denominator equal to zero and solving.
- 0 = x + 3 and 0 = x – 3
  x = 3, -3. The domain of the function is all real numbers x ≠ 3, -3
To find vertical asymptotes refer back to Step 1: now that we have factored the numerator and denominator, we cancel out the common factors.
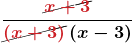
- Then using the simplified denominator (x-3), we determine where this function will be undefined by setting the denominator equal to zero:
  0 = x – 3. So there is a vertical asymptote at x = 3.
- The common factor of (x+3) that was cancelled out is a removable discontinuity. It is represented by a “hole” in the graph below.

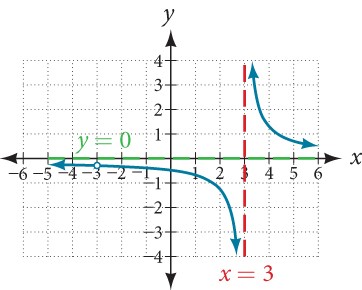
Graph of f(x)=1/(x-3) with its vertical asymptote at x=3 and its horizontal asymptote at y=0. A hole is located along the left side at x = -3.

As shown above not all zeros in the domain will reflect vertical asymptotes. Those zeros that are also common to the numerator will represent “holes” or removable discontinuities in the graph rather than an asymptote in most cases.

Removable Discontinuities of Rational Functions

A removable discontinuity occurs in the graph of a rational function at x = a if a is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value. For more examples refer to Openstax here.

Identifying Horizontal Asymptotes and Intercepts from an Equation

While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the function that is the ratio of the leading terms. There are 3 outcomes when checking for horizontal asymptotes. We will only explore 2 of them in our course.

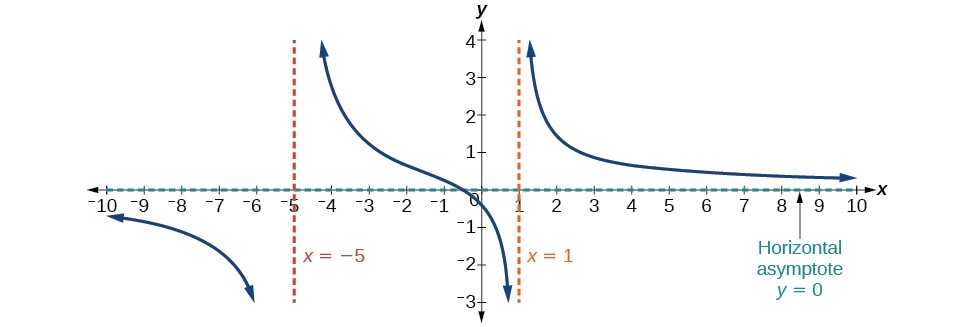
Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at y = 0.

Example: f(x) = $\displaystyle \frac{4x+2}{x^2 + 4x - 5}$ .

In this case, the end behavior is f(x) ≈ $\displaystyle \frac{4x}{x^2} = \frac{4}{x}$ . This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function g(x) = $\displaystyle \frac{4}{x}$ and the outputs will approach zero, resulting in a horizontal asymptote at y = 0.

Graph of f(x) = (4x+2) / (x^2 + 4x-5) with its vertical asymptotes at x= -5 and x= 1 and its horizontal asymptote at y=0.

Case 2: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at y = $\displaystyle \frac{a_n}{b_n}$ where a_n and b_n are the leading coefficients of p(x) and q(x) for f(x) = $\displaystyle \frac{p\left(x\right)}{q\left(x\right)}$ , q(x) ≠ 0.

Example: f(x) = $\displaystyle \frac{3x^2+2}{x^2 + 4x - 5}$ .

In this case, the end behavior is f(x) ≈ $\displaystyle \frac{3x^2}{x^2} = 3$ . This tells us that as the inputs grow large, this function will behave like the function g(x) = 3, which is a horizontal line and results in a horizontal asymptote at y = 3. Note that this graph crosses the horizontal asymptote.

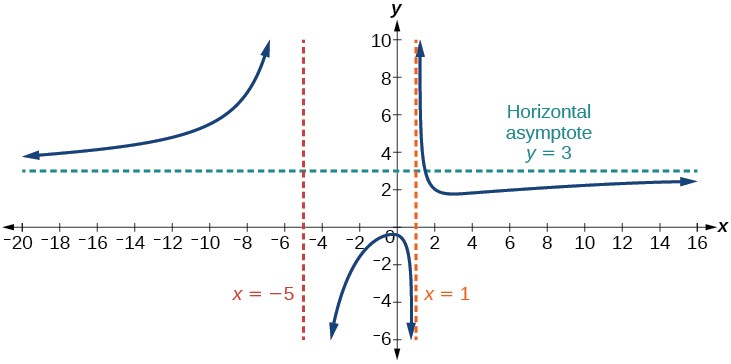
Graph of f(x)=(3x^2+2)/(x^2+4x-5) with its vertical asymptotes at x=-5 and x=1 and its horizontal asymptote at y=3.

Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal asymptote.

There is a 3^rd case called the Slant Asymptote, but we will not use it in our class. You will see this used when the degree of the numerator is greater than degree of denominator by one. For our purposes, you can just list that there is no horizontal asymptote if this occurs. But to see more information about the slant asymptote please refer to the Openstax chapter here.

Horizontal Asymptotes of Rational Functions

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0.
Degree of numerator is greater than degree of denominator by one: no horizontal asymptote.
Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Try it! – Identifying Horizontal Asymptotes

For the functions listed, identify the horizontal asymptote.

a. g(x) = $\displaystyle \frac{6x^3-10x}{2x^3 + 5x^2}$

b. h(x) = $\displaystyle \frac{x^2-4x+1}{x+2}$

c. k(x) = $\displaystyle \frac{x^2+4x}{x^3 - 8}$

Solution

For these solutions, we will use f(x) = $\displaystyle \frac{p\left(x\right)}{q\left(x\right)}$ , q(x) ≠ 0.

Solution A (click to reveal)

a. g(x) = $\displaystyle \frac{6x^3-10x}{2x^3 + 5x^2}$ : The degree of p = degree of q = 3, so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at $\displaystyle \frac{6}{2}$ or y = 3.

Solution B (click to reveal)

b. h(x) = $\displaystyle \frac{x^2-4x+1}{x+2}$ : The degree of p = 2 and degree of q = 1. Since p > q by 1, there is no horizontal asymptote.

Solution C (click to reveal)

c. k(x) = $\displaystyle \frac{x^2+4x}{x^3 - 8}$ : The degree of p = 2 < degree of q = 3, so there is a horizontal asymptote y = 0.

Try it! – Identify both Horizontal and Vertical asymptotes

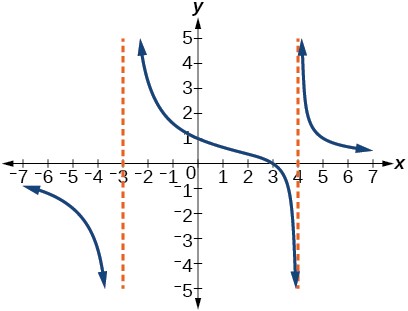
Find the vertical asymptotes, and the horizontal asymptote of the function. f(x) = $\displaystyle 4\frac{x-3}{x^2 - x -12}$

Solution (click to reveal)

Vertical Asymptote: -3, 4. Horizontal Asymptote: 0

Graph of a rational function with vertical asymptotes at x=-3 and x=4.

Try it! –Identify both Horizontal and Vertical Asymptotes and Domain

Find the domain, vertical asymptotes, and horizontal asymptotes of the function:

f(x) = $\displaystyle \frac{2}{5x+2}$

Solution (click to reveal)

V.A. at x = $\displaystyle \frac{-2}{5}$ ; H.A. at y = 0; Domain is all reals x ≠ $\displaystyle \frac{-2}{5}$ .

One other characteristic we can identify from the equation, are the intercepts.

Intercepts of Rational Functions

A rational function will have a y-intercept at f(0), if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero.

Likewise, a rational function will have x-intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x-intercepts can only occur when the numerator of the rational function is equal to zero.

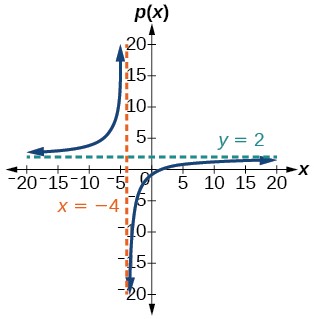
Try it! – Finding the Intercepts & Asymptotes

Find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal asymptote of the function. Use that information to sketch a graph.

p(x) = $\displaystyle \frac{2x-3}{x+4}$ .

Solution (click to reveal)

We can find the y-intercept by evaluating the function at zero

p(0) = $\displaystyle \frac{2\left(0\right)-3}{\left(0\right)+4}$ .

= – $\displaystyle \frac{3}{4}$

The y-intercept is – $\displaystyle \frac{3}{4}$ .

The x-intercepts will occur when the function is equal to zero:

0 = $\displaystyle \frac{2x-3}{x+4}$ (This is zero when the numerator is zero.)

0 = 2x – 3

x = $\displaystyle \frac{3}{2}$

The y-intercept is (0, – $\displaystyle \frac{3}{4}$ ), the x-intercept is ( $\displaystyle \frac{3}{2}$ , 0).

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

0 = x + 4

x = -4, the vertical Asymptote is at x = -4

To find Horizontal asymptotes: The degree of p = degree of q = 1, so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at $\displaystyle \frac{2}{1}$ or y = 2.

Graph of p(x)=(2x-3)/(x+4) with its vertical asymptote at x=-4 and horizontal asymptote at y=2.

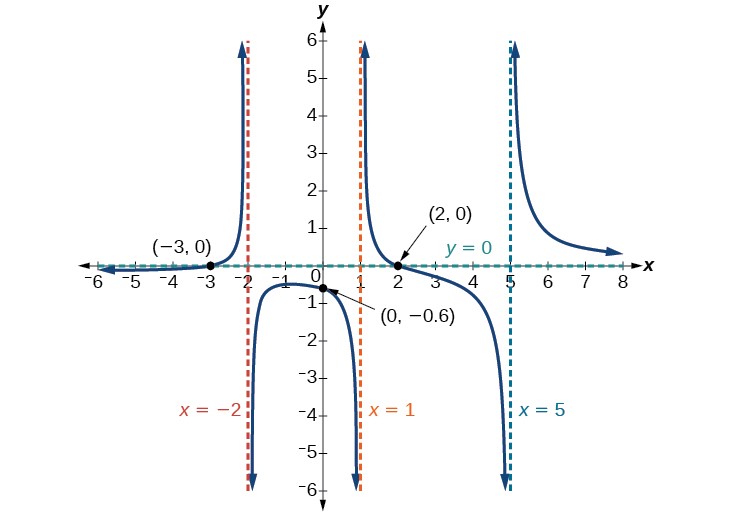
Try it! -Put it all together

Find the intercepts and Asymptotes of f(x) = $\displaystyle \frac{\left(x-2\right)\left(x+3\right)}{\left(x-1\right)\left(x+2\right)\left(x-5\right)}$

Solution (click to reveal)

We can find the y-intercept by evaluating the function at zero

f(0) = $\displaystyle \frac{\left(0-2\right)\left(0+3\right)}{\left(0-1\right)\left(0+2\right)\left(0-5\right)}$

= – $\displaystyle \frac{6}{10}$

= – $\displaystyle \frac{3}{5}$

= −0.6

The x-intercepts will occur when the function is equal to zero:

0 = $\displaystyle \frac{\left(x-2\right)\left(x+3\right)}{\left(x-1\right)\left(x+2\right)\left(x-5\right)}$ This is zero when the numerator is zero.

0 = (x−2) (x+3)

x=2,−3

The y-intercept is (0,–0.6), the x-intercepts are (2,0) and (–3,0).

Asymptotes:

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at x = 1, –2, and 5, indicating vertical asymptotes at these values.

To find Horizontal asymptotes: The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large. This function will have a horizontal asymptote at y = 0.

Graph of f(x)=(x-2)(x+3)/(x-1)(x+2)(x-5) with its vertical asymptotes at x=-2, x=1, and x=5, its horizontal asymptote at y=0, and its intercepts at (-3, 0), (0, -0.6), and (2, 0).

Graphing Rational Functions

In previous examples we saw that the numerator of a rational function reveals the x-intercepts of the graph, whereas the denominator reveals the vertical asymptotes of the graph. As with polynomials, factors of the numerator may have integer powers greater than one. Fortunately, the effect on the shape of the graph at those intercepts is the same as we saw with polynomials.

The vertical asymptotes associated with the factors of the denominator will mirror one of the two toolkit reciprocal functions. When the degree of the factor in the denominator is odd, the distinguishing characteristic is that on one side of the vertical asymptote the graph heads towards positive infinity, and on the other side the graph heads towards negative infinity.

Graph of y=1/x with its vertical asymptote at x=0.

When the degree of the factor in the denominator is even, the distinguishing characteristic is that the graph either heads toward positive infinity on both sides of the vertical asymptote or heads toward negative infinity on both sides.

Graph of y=1/x^2 with its vertical asymptote at x=0.

For example, the graph of f(x) = $\displaystyle \frac{\left(x+1\right)^2\left(x-3\right)}{\left(x+3\right)^2\left(x-2\right)}$ .

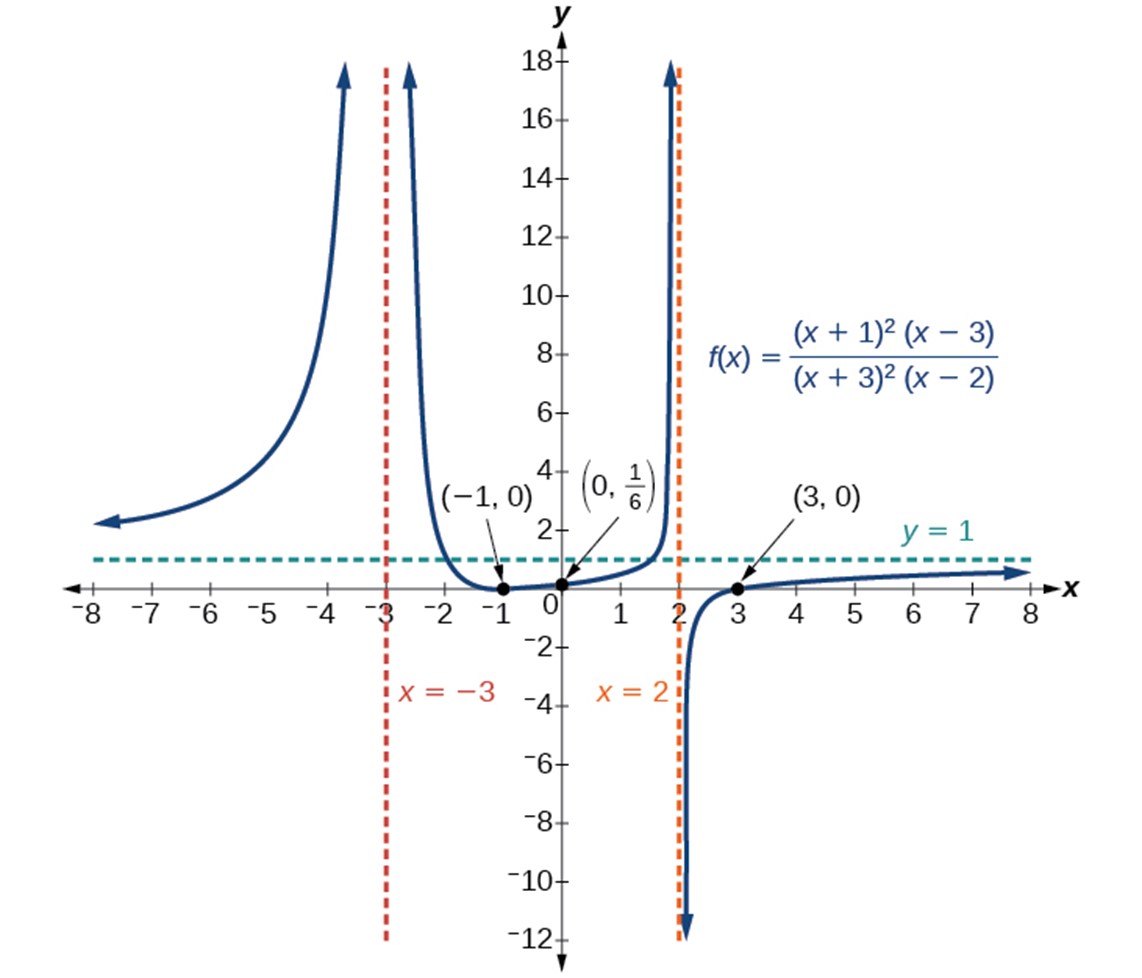
"Graph of f(x)=(x+1)^2(x-3)/(x+3)^2(x-2) with its vertical asymptotes at x=-3 and x=2, its horizontal asymptote at y=1, and its intercepts at (-1, 0), (0, 1/6), and (3, 0)."

At the x-intercept x = −1 corresponding to the (x+1)² factor of the numerator, the graph “bounces”, consistent with the quadratic nature of the factor.
At the x-intercept x = 3 corresponding to the (x−3) factor of the numerator, the graph passes through the axis as we would expect from a linear factor.
At the vertical asymptote x=−3 corresponding to the (x+3)² factor of the denominator, the graph heads towards positive infinity on both sides of the asymptote, consistent with the behavior of the function f(x) = $\displaystyle \frac{1}{x^2}$ .
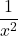At the vertical asymptote x = 2, corresponding to the (x−2) factor of the denominator, the graph heads towards positive infinity on the left side of the asymptote and towards negative infinity on the right side.

How To: Given a rational function, sketch a graph.

Evaluate the function at 0 to find the y-intercept.
Factor the numerator and denominator.
For factors in the numerator not common to the denominator, determine where each factor of the numerator is zero to find the x-intercepts.
Find the multiplicities of the x-intercepts to determine the behavior of the graph at those points.
For factors in the denominator, note the multiplicities of the zeros to determine the local behavior. For those factors not common to the numerator, find the vertical asymptotes by setting those factors equal to zero and then solve.
For factors in the denominator common to factors in the numerator, find the removable discontinuities by setting those factors equal to 0 and then solve.
Compare the degrees of the numerator and the denominator to determine the horizontal or slant asymptotes.
Sketch the graph.

Try it!

Find the intercepts, vertical asymptotes, and horizontal asymptotes of the function, then sketch the graph: f(x) = $\displaystyle \frac{\left(x+2\right)\left(x-3\right)}{\left(x+1\right)^2\left(x-2\right)}$ .

Solution (click to reveal)

We can find the y-intercept by evaluating the function at zero:

f(0) = $\displaystyle \frac{\left(0+2\right)\left(0-3\right)}{\left(0+1\right)^2\left(0-2\right)}$ .

= $\displaystyle \frac{3}{1}$

= 3

The x-intercepts will occur when the function is equal to zero:

0 = x+2 and 0 = x – 3. This is zero when the numerator is zero.

x = -2, 3

The y-intercept is (0, 3), the x-intercept is (-2, 0) and (3,0). The end behavior at the x-intercepts is linear (multiplicity 1), with the graph passing through it.

Asymptotes:

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. We determine where this function will be undefined by setting the denominator equal to zero.

0 = x + 1 and 0 = x – 2

x = -1, and 2. The denominator will be zero at x = -1, 2.

To find Horizontal asymptotes: The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large. This function will have a horizontal asymptote at y = 0.

Sketch:

We might start by plotting the three intercepts. Since the graph has no x-intercepts between the vertical asymptotes, and the y-intercept is positive, we know the function must remain positive between the asymptotes, letting us fill in the middle portion of the graph.

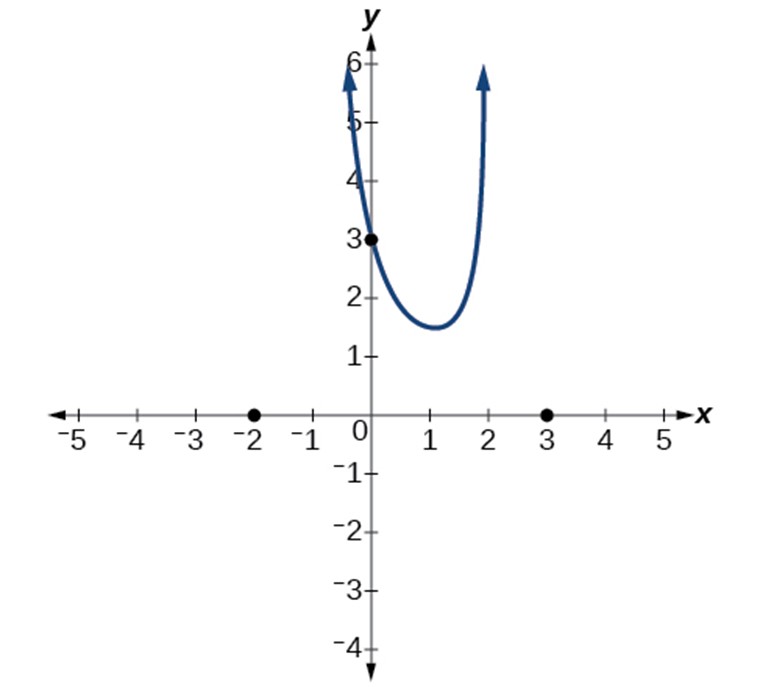
"Graph of only the middle portion of f(x)=(x+2)(x-3)/(x+1)^2(x-2) with its intercepts at (-2, 0), (0, 3), and (3, 0)."

The factor associated with the vertical asymptote at x = −1 was squared, so we know the behavior will be the same on both sides of the asymptote. The graph heads toward positive infinity as the inputs approach the asymptote on the right, so the graph will head toward positive infinity on the left as well.

For the vertical asymptote at x = 2, the factor was not squared, so the graph will have opposite behavior on either side of the asymptote. After passing through the x-intercepts, the graph will then level off toward an output of zero, as indicated by the horizontal asymptote.

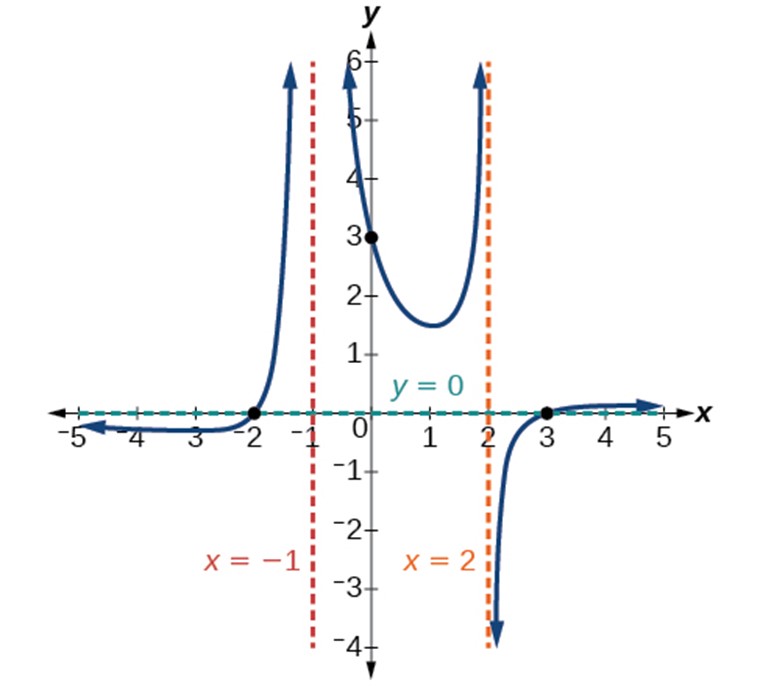
Graph of f(x)=(x+2)(x-3)/(x+1)^2(x-2) with its vertical asymptotes at x=-1 and x=2, its horizontal asymptote at y=0, and its intercepts at (-2, 0), (0, 3), and (3, 0).

Try it!

Find the domain, vertical asymptotes, and horizontal asymptotes of the function, the sketch the graph: s(x) = $\displaystyle \frac{4}{\left(x-2\right)^2}$ .

Solution (click to reveal)

We can find the y-intercept by evaluating the function at zero:

f(0) = $\displaystyle \frac{4}{\left(0-2\right)^2}$ .

= $\displaystyle \frac{4}{4}$

= 1

The x-intercepts will occur when the function is equal to zero: 0 ≠ 4. As the numerator is a constant, we cannot set it to zero to solve. In this case, there would be no x-intercept.

The y-intercept is (0, 1).

Asymptotes:

The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. We determine where this function will be undefined by setting the denominator equal to zero.

0 = (x – 2)²

x = 2. The denominator will be zero at x = 2.

To find Horizontal asymptotes: The numerator has degree 0, while the denominator has degree 2. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large. This function will have a horizontal asymptote at y = 0.

Sketch:

We might start by plotting the intercept.

The factor associated with the vertical asymptote at x = 2 was squared, so we know the behavior will be the same on both sides of the asymptote. The graph heads toward positive infinity as the inputs approach the asymptote on the right, so the graph will head toward positive infinity on the left as well.

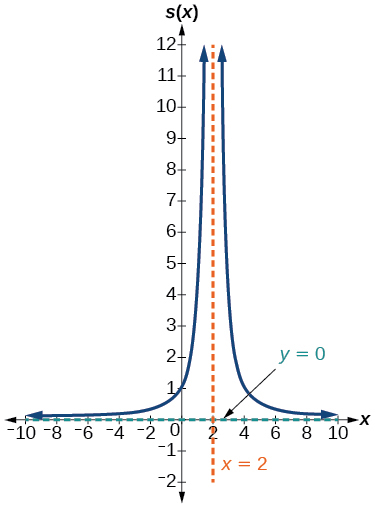
Graph of s(x)=4/(x-2)^2 with its vertical asymptote at x=2 and horizontal asymptote at y=0.

Try it

Find the domain, vertical asymptotes, and horizontal asymptotes of the function, the sketch the graph:
f(x) = $\displaystyle \frac{x+2}{x-5}$ .

Solution (click to reveal)

Intercepts (–2,0) and (0,− $\displaystyle \frac{2}{5}$ ) , Asymptotes x = 5 and y = 1.

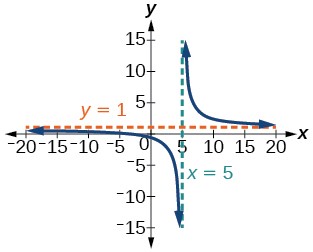
Graph of f(x)=(x+1)/(x-5).

Key Concepts

- How to Solve Equations with Fraction or Decimal Coefficients
  1. Find the least common denominator (LCD) of all the fractions and decimals (in fraction form) in the equation.
  2. Multiply both sides of the equation by that LCD. This clears the fractions and decimals.
  3. Solve using the General Strategy for Solving Linear Equations.
- The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.
- The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero.
- A rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
- Graph rational functions by finding the intercepts, behavior at the intercepts and asymptotes, and end behavior.

Derived from Openstax Intermediate Algebra, Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction. Also College Algebra 2e with Corequisite Supports, Access for free at https://openstax.org/books/college-algebra-corequisite-support-2e/pages/1-introduction-to-prerequisites ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Solve Rational Equations

Characteristics of Rational Functions

Identifying Vertical Asymptotes, and Domain from an Equation

Identifying Horizontal Asymptotes and Intercepts from an Equation

Graphing Rational Functions

License

Share This Book