Inverse Functions

Elizabeth Pople

16 Inverse Functions

Topics Covered

By the end of this section, you will be able to:

Determine whether a function is one-to-one
Find the inverse of a function

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

One-to-One Functions
Define Inverse of a Function
Find Inverse of a Function
Key Concepts

Determine Whether a Function is One-to-One

When we first introduced functions, we said a function is a relation that assigns to each element in its domain exactly one element in the range. For each ordered pair in the relation, each x-value is matched with only one y-value.

We used the birthday example to help us understand the definition. Every person has a birthday, but no one has two birthdays and it is okay for two people to share a birthday. Since each person has exactly one birthday, that relation is a function.

A function is one-to-one if each value in the range has exactly one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value.

Our example of the birthday relation is not a one-to-one function. Two people can share the same birthday. The range value August 2 is the birthday of Liz and June, and so one range value has two domain values. Therefore, the function is not one-to-one.

One-to-One Function

A function is one-to-one if each value in the range corresponds to one element in the domain. For each ordered pair in the function, each y-value is matched with only one x-value. There are no repeated y-values.

Try it!

For each set of ordered pairs, determine if it represents a function and, if so, if the function is one-to-one.

a. {(−3, 27), (−2, 8), (−1, 1), (0, 0), (1, 1), (2, 8), (3, 27)} and b. {(0, 0), (1, 1), (4, 2), (9, 3), (16, 4)}.

Solution:

a. {(−3, 27), (−2, 8), (−1, 1), (0, 0), (1, 1), (2, 8), (3, 27)}

Each x-value is matched with only one y-value. So this relation is a function.

But each y-value is not paired with only one x-value, (−3, 27) and (3, 27), for example. So this function is not one-to-one.

b. {(0, 0), (1, 1), (4, 2), (9, 3), (16, 4)}

Each x-value is matched with only one y-value. So this relation is a function.

Since each y-value is paired with only one x-value, this function is one-to-one.

2. For each set of ordered pairs, determine if it represents a function and if so, is the function one-to-one.

a. {(−3, −6), (−2, −4), (−1, −2), (0, 0), (1, 2), (2, 4), (3, 6)} b. {(−4, 8), (−2, 4), (−1, 2), (0, 0), (1, 2), (2, 4), (4, 8)}

Solution:

a. One-to-one function
b. Function; not one-to-one

To help us determine whether a relation is a function, we use the vertical line test. A set of points in a rectangular coordinate system is the graph of a function if every vertical line intersects the graph in at most one point. Also, if any vertical line intersects the graph in more than one point, the graph does not represent a function.

The vertical line is representing an x-value and we check that it intersects the graph in only one y-value. Then it is a function.

To check if a function is one-to-one, we use a similar process. We use a horizontal line and check that each horizontal line intersects the graph in only one point. The horizontal line is representing a y-value and we check that it intersects the graph in only one x-value. If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function. This is the horizontal line test.

Horizontal Line Test

If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function.

We can test whether a graph of a relation is a function by using the vertical line test. We can then tell if the function is one-to-one by applying the horizontal line test.

Try it!

Determine a. whether each graph is the graph of a function and, if so, b. whether it is one-to-one.

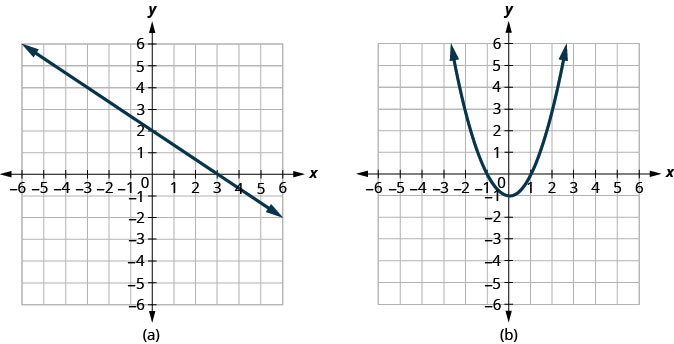
This first graph shows a straight line passing through (0, 2) and (3, 0). This second shows a parabola opening up with vertex at (0, negative 1).

Solution:

a.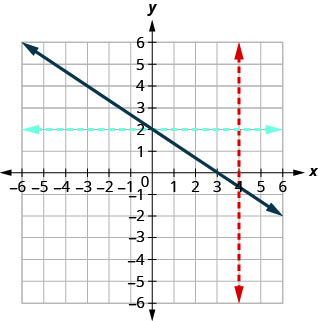 This figure shows a straight line passing through (0, 2) and (3, 0), with a red vertical line that only passes through one point and a blue horizontal line that only passes through one point. Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. Since any horizontal line intersects the graph in at most one point, the graph is the graph of a one-to-one function.

b.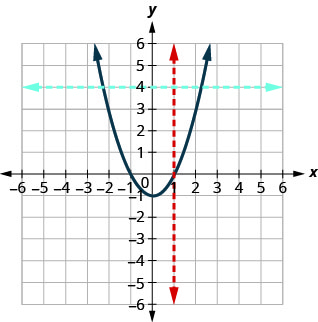 This figure shows a parabola opening up with vertex at (0, negative 1), with a red vertical line that only passes through one point and a blue horizontal line that passes through two points. Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. The horizontal line shown on the graph intersects it in two points. This graph does not represent a one-to-one function.

2. Determine a. whether each graph is the graph of a function and, if so, b. whether it is one-to-one.

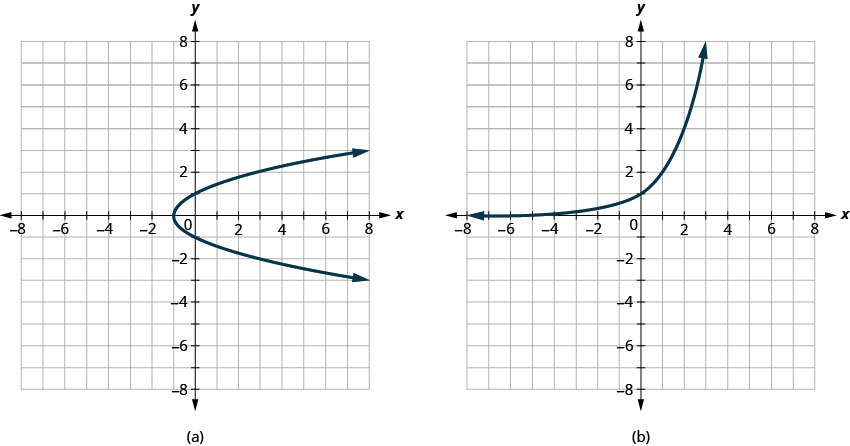
Graph a shows a parabola opening to the right with vertex at (negative 1, 0). Graph b shows an exponential function that does not cross the x axis and that passes through (0, 1) before increasing rapidly.

Solution:

a. Not a function b. One-to-one function

Defining the Inverse of a Function

Let’s look at a one-to one function, f, represented by the ordered pairs {(0, 5), (1, 6), (2, 7), (3, 8)}. For each x-value, f adds 5 to get the y-value. To ‘undo’ the addition of 5, we subtract 5 from each y-value and get back to the original x-value. We can call this “taking the inverse of f” and name the function f⁻¹.
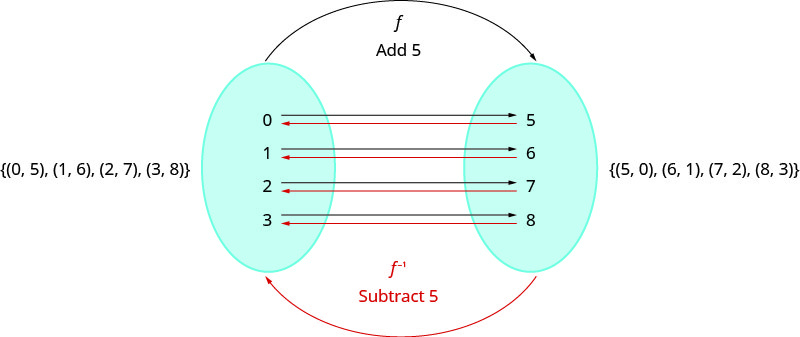Notice that that the ordered pairs of f and f⁻¹ have their x-values and y-values reversed. The domain of f is the range of f⁻¹ and the domain of f⁻¹ is the range of f.

Inverse of a Function Defined by Ordered Pairs

If f(x) is a one-to-one function whose ordered pairs are of the form (x,y), then its inverse function f⁻¹(x) is the set of ordered pairs (y,x).

The range of a function f(x) is the domain of the inverse function f⁻¹(x).

The domain of f(x) is the range of f⁻¹(x).

In the next example we will find the inverse of a function defined by ordered pairs.

Try it!

Find the inverse of the function {(0, 3), (1, 5), (2, 7), (3, 9)}. Determine the domain and range of the inverse function.

Solution:

This function is one-to-one since every x-value is paired with exactly one y-value.

To find the inverse we reverse the x-values and y-values in the ordered pairs of the function.

Question

Solution

Function

{(0,3),(1,5),(2,7),(3,9)}

Inverse Function

{(3,0),(5,1),(7,2),(9,3)}

Domain of Inverse Function

{3,5,7,9}

Range of Inverse Function

{0,1,2,3}

2. Find the inverse of {(0, 4), (1, 7), (2, 10), (3, 13)}. Determine the domain and range of the inverse function.

Solution:

Inverse function: {(4, 0), (7, 1), (10, 2), (13, 3)}. Domain: {4, 7, 10, 13}. Range: {0, 1, 2, 3}.

Since every point on the graph of a function f(x) is a mirror image of a point on the graph of f⁻¹(x),we say the graphs are mirror images of each other through the line y=x. We will use this concept to graph the inverse of a function in the next example.

Try it!

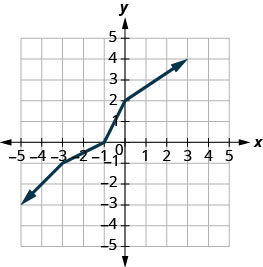
Graph, on the same coordinate system, the inverse of the one-to one function shown.

This figure shows a line from (negative 5, negative 3) to (negative 3, negative 1) then to (negative 1,0) then to (0,2) and then to (3, 4).

Solution:

We can use points on the graph to find points on the inverse graph. Some points on the graph are: (−5, −3), (−3, −1), (−1, 0), (0, 2), (3, 4).

So, the inverse function will contain the points: (−3, −5), (−1, −3), (0, −1), (2, 0), (4, 3).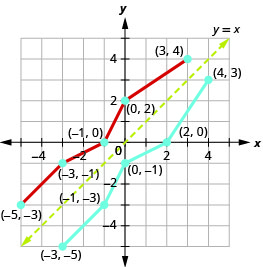 This figure shows a line from (negative 5, negative 3) to (negative 3, negative 1) then to (negative 1, 0) then to (0,2) and then to (3, 4). Then there is a dashed line to denote y equals x. There is also a line from (negative 3, negative 5) to (negative 1, negative 3) then to (0, negative 1), then to (2, 0) and then to (4, 3). Notice how the graph of the original function and the graph of the inverse functions are mirror images through the line y = x.

Given a function f(x), we represent its inverse as f⁻¹(x), read as “f inverse of x.” The raised −1 is part of the notation. It is not an exponent; it does not imply a power of −1. In other words, f⁻¹(x) does not mean $\displaystyle\frac{1}{f(x)}$ because $\displaystyle\frac{1}{f(x)}$ is the reciprocal of f and not the inverse.

The “exponent-like” notation comes from an analogy between function composition and multiplication: just as a⁻¹a=1 (1 is the identity element for multiplication) for any nonzero number a, so f⁻¹∘f equals the identity function, that is,

(f⁻¹∘f)(x) = f⁻¹(f(x)) = f⁻¹(y) = x

Inverse Functions

For any one-to-one function f(x)=y, a function f⁻¹(x) is an inverse function of f if f⁻¹(y)=x. This can also be written as f⁻¹(f(x))=x for all x in the domain of f. It also follows that f(f⁻¹(x))=x for all x in the domain of f⁻¹ if f⁻¹ is the inverse of f.

The notation f⁻¹ is read “f inverse.” Like any other function, we can use any variable name as the input for f⁻¹, so we will often write f⁻¹(x), which we read as “f inverse of x.” Keep in mind that $\displaystyle f^{-1} \neq \frac{1}{f(x)}$ and not all functions have inverses.

Inverse function, which is a function for which the input of the original function becomes the output of the inverse function and the output of the original function becomes the input of the inverse function.

f⁻¹(f(x)) = x, for all x in the domain of f

f(f⁻¹(x)) = x, for all x in the domain of f⁻¹

When we began our discussion of an inverse function, we talked about how the inverse function ‘undoes’ what the original function did to a value in its domain in order to get back to the original x-value. This holds for all x in the domain of f. Informally, this means that inverse functions “undo” each other. However, just as zero does not have a reciprocal, some functions do not have inverses.

For example, y = 4x and y = $\displaystyle\frac{1}{4}$ (x) are inverse functions.

(f⁻¹∘f)(x) = f⁻¹(4x) = $\displaystyle\frac{1}{4}$ (4x) = x

and

(f∘f⁻¹)(x) = f( $\displaystyle\frac{1}{4}$ x)=4( $\displaystyle\frac{1}{4}$ x) = x

We can use this property to verify that two functions are inverses of each other.

How To

Given two functions f(x) and g(x), test whether the functions are inverses of each other.

Determine whether f(g(x)) = x or g(f(x)) = x.
If either statement is true, then both are true, and g = f⁻¹and f = g⁻¹. If either statement is false, then both are false, and g ≠ f⁻¹and f ≠ g⁻¹.

Try it!

Verify that f(x) = 5x − 1 and g(x) = $\displaystyle\frac{x + 1}{5}$ are inverse functions.

Solution:

The functions are inverses of each other if g(f(x)) = x and f(g(x)) = x.

Steps

Algebraic

Substitute 5x − 1 for f(x).

Simplify.

Substitute $\displaystyle\frac{x + 1}{5}$ for g(x).

Simplify.

Since both g(f(x)) = x and f(g(x)) = x are true, the functions f(x) = 5x − 1 and g(x) = $\displaystyle\frac{x + 1}{5}$ are inverse functions. That is, they are inverses of each other.

2. Verify that the functions are inverse functions.

f(x) = 4x − 3 and g(x) = $\displaystyle\frac{x + 3}{4}$ .

Solution:

g(f(x)) = x, and f(g(x)) = x, so they are inverses.

3. Verify that the functions are inverse functions.

f(x)=2x + 6 and g(x)= $\displaystyle\frac{x - 6}{2}$ .

Solution:

g(f(x))=x, and f(g(x))=x, so they are inverses.

Try it! – Testing Inverse Relationships Algebraically

If f(x) = 1x + 2 and g(x) = 1x − 2, is g = f⁻¹?

Solution:

g(f(x)) = $\displaystyle\frac{1}{(\frac{1}{x+2})} - 2$

= x + 2 − 2

= x

so

g = f⁻¹and f = g⁻¹

This is enough to answer yes to the question, but we can also verify the other formula.

f(g(x)) = $\displaystyle\frac{1}{\frac{1}{x} - 2 + 2}$

= $\displaystyle\frac{1}{\frac{1}{x}}$

=x

Analysis Notice the inverse operations are in reverse order of the operations from the original function.

Finding the Inverse of a Function

We have found inverses of function defined by ordered pairs and from a graph. We will now look at how to find an inverse using an algebraic equation. The method uses the idea that if f(x) is a one-to-one function with ordered pairs (x,y),

then its inverse function f⁻¹(x) is the set of ordered pairs (y, x).

If we reverse the x and y in the function and then solve for y, we get our inverse function.

How To Find the Inverse

Substitute y for f(x).
Interchange the variables x and y.
Solve for y.
Substitute f⁻¹(x) for y.
Verify that the functions are inverses.

Try it! – How to Find the inverse of a One-to-One Function

Find the inverse of f(x) = 4x + 7.

Solution:

Step 1 is to substitute y for f of x. To do so, we replace f of x with y. Hence, f of x equals 4 x plus 7 becomes y equals 4 x plus 7.

Step 3 is to solve for y. To do so, we subtract 7 from each side and then divide by 4. Hence, we have x minus 7 equals 4y and then the quantity x minus 7 divided by 4 equals y.

Step 5 is to verify that the functions are inverses. To do so, we show that f superscript negative 1 of f of x equals x and that f of f superscript negative 1of x equals x. Hence, we ask whether f inverse of 4x plus 7 equals x. This becomes a question of whether 4 x plus 7 minus 7 all divided by 4 equals x. This becomes a question of whether 4x divided by 4 equals x. This is true. To show the other side, we examine whether f of f inverse of x equals x. This becomes a question of whether f of the quantity x minus 7 divided by 4 equals x. This becomes a question of whether 4 times the quantity x minus 7 divided by 4 equals x. This becomes a question of whether x minus 7 plus 7 equals x. This is true.

2. Find the inverse of the function f(x) = 5x − 3.

Solution:

f⁻¹(x) = $\displaystyle\frac{x + 3}{5}$

Try it! – How to Find the Inverse of a One-to-One Function

Find the inverse of f(x) = 2x − 35.

Solution:

Steps

Algebraic

f(x) = $\displaystyle \sqrt[5]{2x - 3}$

Substitute y for f(x).

y = $\displaystyle \sqrt[5]{2x - 3}$

Interchange the variables x and y.

x = $\displaystyle \sqrt[5]{2y - 3}$

Solve for y.

$\displaystyle (x)^5 = (\sqrt[5]{2y - 3})^5$

$\displaystyle x^5 = {2y - 3}$

$\displaystyle x^5 + 3 = {2y}$

$\displaystyle \frac{x^5 + 3}{2} = {y}$

Substitute f^-1(x) for y.

f^-1(x) = $\displaystyle \frac{x^5 + 3}{2}$

Verify that the functions are inverses.

Steps

Algebraic

f^-1(f(x)) = x

f(f^-1(x) = x

$\displaystyle f^{-1}(\sqrt[5]{2x - 3}) = x$

$\displaystyle f(\frac{x^5 + 3}{2}) = {x}$

$\displaystyle \frac{(\sqrt[5]{2x - 3})^5 + 3}{2} = {x}$

$\displaystyle \sqrt[5]{2(\frac{x^5 + 3}{2}) - 3} = x$

$\displaystyle \frac{2x - 3 + 3}{2} = {x}$

$\displaystyle \sqrt[5]{x^5 + 3 - 3} = x$

$\displaystyle \frac{2x}{2} = {x}$

$\displaystyle \sqrt[5]{x^5} = x$

x = x ✓

2. Find the inverse of the function $\displaystyle f(x) = \sqrt[4]{6x - 7}$

Solution:

f^-1(x) = $\displaystyle \frac{x^4 + 7}{6}$

3. $\displaystyle f(x) = \frac{x}{x + 2}$

Solution:

f^-1(x) = $\displaystyle \frac{-2x}{x - 1}$

Key Concepts

Composition of Functions: The composition of functions f and g, is written f ∘ g and is defined by

(f∘g)(x) = f(g(x))

We read f(g(x)) as f of g of x.
Horizontal Line Test: If every horizontal line, intersects the graph of a function in at most one point, it is a one-to-one function.
Inverse of a Function Defined by Ordered Pairs: If f(x) is a one-to-one function whose ordered pairs are of the form (x,y), then its inverse function f⁻¹(x) is the set of ordered pairs (y,x).
Inverse Functions: For every x in the domain of one-to-one function f and f^-1.
f^-1(f(x)) = x

f(f^-1(x)) = x

How to Find the Inverse of a One-to-One Function:
1. Substitute y for f(x).
2. Interchange the variables x and y.
3. Solve for y.
4. Substitute f^-1(x) for y.
5. Verify that the functions are inverses.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Determine Whether a Function is One-to-One

Defining the Inverse of a Function

Inverse of a Function Defined by Ordered Pairs

Inverse Functions

How To

Finding the Inverse of a Function

How To Find the Inverse

License

Share This Book