1 Foundations (Integers and Language of Algebra )
Topics Covered:[1]
This module provides a review of those topics needed prior to the start of the semester. Here is a list of topics covered:
Identify Counting Numbers and Whole Numbers
Learning algebra is similar to learning a language. You start with a basic vocabulary and then add to it as you go along. You need to practice often until the vocabulary becomes easy to you. The more you use the vocabulary, the more familiar it becomes.
Algebra uses numbers and symbols to represent words and ideas. Let’s look at the numbers first. The most basic numbers used in algebra are those we use to count objects: 1, 2, 3, 4, 5, … and so on. These are called counting numbers. The notation “…” is called an ellipsis, which is another way to show “and so on”, or that the pattern continues endlessly. Counting numbers are also called natural numbers.
Counting numbers start with 1 and continue.
1, 2, 3, 4, 5, …
Counting numbers and whole numbers can be visualized on a number line as shown below.
The point labeled 0 is called the origin. The points are equally spaced to the right of 0 and labeled with the counting numbers. When a number is paired with a point, it is called the coordinate of the point.
The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called whole numbers.
Whole numbers are counting numbers and zero.
Try it!
Which of the following are:
a. counting numbers?
b. whole numbers?
0, ![]() , 3, 5.2, 15, 105
, 3, 5.2, 15, 105
Solution (click to reveal)
a) Counting numbers start at 1, so 0 is not a counting number. The numbers 3, 15, and 105 are all counting numbers.
b. Whole numbers are counting numbers and 0. The numbers 0, 3, 15, and 105 are whole numbers. The numbers ![]() and 5.2 are neither counting numbers nor whole numbers. We will discuss these numbers later.
and 5.2 are neither counting numbers nor whole numbers. We will discuss these numbers later.
Use Variables and Algebraic Symbols
Greg and Alex have the same birthday, but they were born in different years. This year Greg is 20 years old and Alex is 23, so Alex is 3 years older than Greg. When Greg was 12, Alex was 15. When Greg is 35, Alex will be 38. No matter what Greg’s age is, Alex’s age will always be 3 years more, right?
In the language of algebra, we say that Greg’s age and Alex’s age are variable and the three is a constant. The ages change or vary, so age is a variable. The 3 years between them always stay the same, so the age difference is the constant.
In algebra, letters of the alphabet are used to represent variables. Suppose we call Greg’s age g. Then we could use g + 3 to represent Alex’s age. See table below.
| Greg’s age | Alex’s age |
|---|---|
| 12 | 15 |
| 20 | 23 |
| 35 | 38 |
| g | g + 3 |
Letters are used to represent variables. Letters often used for variables are x, y, a, b, and c.
A variable is a letter that represents a number or quantity whose value may change.
A constant is a number whose value always stays the same.
To write algebraically, we need some symbols as well as numbers and variables. There are several types of symbols we will be using. We will summarize the four basic arithmetic operations: addition, subtraction, multiplication, and division in the table below, along with words we use for the operations and the result.
| Operation | Notation | Say: | The result is… |
|---|---|---|---|
| Addition | a plus b | the sum of a and b | |
| Subtraction | a minus b | the difference of a and b | |
| Multiplication | a times b | The product of a and b | |
| Division | |
a divided by b | The quotient of a and b |
In algebra, the cross symbol, ![]() , is not used to show multiplication because that symbol may cause confusion. Does 3xy mean (three times y) or 3
, is not used to show multiplication because that symbol may cause confusion. Does 3xy mean (three times y) or 3 ![]() x
x ![]() y (three times x times y)? To make it clear, use • or parentheses for multiplication.
y (three times x times y)? To make it clear, use • or parentheses for multiplication.
We perform these operations on two numbers. When translating from symbolic form to words, or from words to symbolic form, pay attention to the words of or and to help you find the numbers.
The sum of 5 and 3 means add 5 plus 3, which we write as 5 + 3.
The difference of 9 and 2 means subtract 9 minus 2, which we write as 9 – 2.
The product of 4 and 8 means multiply 4 times 8, which we can write as 4 ![]() 8.
8.
The quotient of 20 and 5 means divide 20 by 5, which we can write as 20 ![]() 5.
5.
When two quantities have the same value, we say they are equal and connect them with an equal sign.
a = b is read a is equal to b.
The symbol = is called the equal sign.
An inequality is used in algebra to compare two quantities that may have different values. The number line can help you understand inequalities. Remember that on the number line the numbers get larger as they go from left to right. So if we know that b is greater than a, it means that b is to the right of a on the number line. We use the symbols “<” and “>” for inequalities.
Inequality:
a < b is read a is less than b
a is to the left of b on the number line
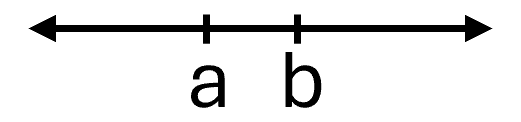
a > b is read a is greater than b
b is to the left of a on the number line
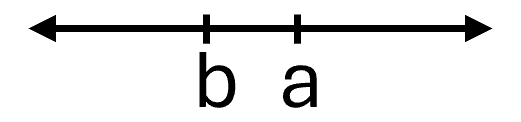
The expressions a < b and a > b can be read from left-to-right or right-to-left, though in English we usually read from left-to-right. This is demonstrated in the table below.
| Algebraic Notation | Say |
| a < b is equivalent to b > a | For example, 7 < 11 is equivalent to 11 > 7. |
| a > b is equivalent to b < a | For example, 17 > 4 is equivalent to 4 < 17. |
When we write an inequality symbol with a line under it, such as a ≤ b, it means a < b or a = b. We read this as a is less than or equal to b. Also, if we put a slash through an equal sign, ≠, it means not equal.
We summarize the symbols of equality and inequality in the table below.
| Algebraic Notation | Say |
|---|---|
| a = b | a is equal to b |
| a ≠ b | a is not equal to b |
| a < b | a is less than b |
| a > b | a is greater than b |
| a ≤ b | a is less than or equal to b |
| a ≥ b | a is greater than or equal to b |
Symbols < and >: The symbols < and > each have a smaller side and a larger side.
The smaller side of the symbol faces the smaller number and the larger faces the larger number.
smaller side < larger side
larger side > smaller side
Try it!
Translate from algebra to words:
a. 20 ≤ 35 b. 11 ≠ 15 − 3 c. 9 > 10 ÷ 2 d. x + 2 < 10
Solution A (click to reveal)
a. 20 ≤ 35
20 is less than or equal to 35
Solution B (click to reveal)
11 is not equal to 15 minus 3
Solution C (click to reveal)
9 is greater than 10 divided by 2
Solution D (click to reveal)
x plus 2 is less than 10
| Description of Symbol | Algebraic Symbol |
|---|---|
| parentheses | ( ) |
| brackets | [ ] |
| braces | { } |
Here are some examples of expressions that include grouping symbols. We will simplify expressions like these later in this section..
8(14 − 8)
21 − 3[2 + 4(9 − 8)]
24 ÷ {13 − 2[1(6 − 5) + 4]}
Use Negatives and Opposites
Our work so far has only included the counting numbers and the whole numbers. But if you have ever experienced a temperature below zero or accidentally overdrawn your checking account, you are already familiar with negative numbers. Negative numbers are numbers less than 0. The negative numbers are to the left of zero on the number line.
![Rendered by QuickLaTeX.com \[\LARGE{ \begin{center} \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{-4 \quad -3 \quad -2 \quad -1\quad 0 \quad 1 \quad 2 \quad 3 \quad 4} \\ \;{\color{mypurple1}\underbrace{\quad{\quad\quad\quad\quad\quad\quad\quad\quad }}_{\boldsymbol{\textcolor{black}{{Negative Numbers}}}}\textbf{Zero}{\color{mypurple1}\underbrace{\quad{\quad\quad \quad\quad\quad\quad\quad }}_{\boldsymbol{\textcolor{black}{{Positive Numbers}}}}\\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4a9d1a575d1bb9be1740cbc9e793ff43_l3.png)
The arrows on the ends of the number line indicate that the numbers keep going forever. There is no biggest positive number, and there is no smallest negative number.
Is zero a positive or a negative number? Numbers larger than zero are positive, and numbers smaller than zero are negative. Zero is neither positive nor negative.
Consider how numbers are ordered on the number line. Going from left to right, the numbers increase in value. Going from right to left, the numbers decrease in value.
![Rendered by QuickLaTeX.com \[\Large{ \begin{aligned} &\quad \quad\quad \quad \quad\color{myblue1}\xrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\phantom{0} \textbf{larger} \\ &\phantom{\text{----}} \overleftrightarrow{ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \quad\quad\quad} \\ &\phantom{\text{------}} \textbf{-4 \quad -3 \quad -2 \quad -1\quad 0 \quad 1 \quad 2 \quad 3 \quad 4} \\ &\quad \textbf{smaller}\phantom{0} \color{myred1}\xleftarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \end{aligned} }\] \caption{\textit{The numbers on a number line increase in value going from left to right and decrease in value going from right to left.}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5433783ec01e56388178d9df48da564b_l3.png)
Remember that we use the notation:
a < b (read “a is less than b”) when a is to the left of b on the number line.
a > b (read “a is greater than b”) when a is to the right of b on the number line.
Now we need to extend the number line which showed the whole numbers to include negative numbers, too. The numbers marked by points in the image below are called the integers. The integers are the numbers …−3, −2, −1, 0, 1, 2, 3 …

Try it!
Order each of the following pairs of numbers, using < or >:
a. 14![]() 6
6
b. −1![]() 9
9
c. −1![]() −4
−4
d. 2![]() −20.
−20.
Solution (click to reveal)
It may be helpful to refer to the number line shown.

| Steps |
Algebraic |
| a. 14 is to the right of 6 on the number line. | 14 |
| b. −1 is to the left of 9 on the number line. | −1 |
| c. −1 is to the right of −4 on the number line. | −1 |
| d. 2 is to the right of −20 on the number line. | 2 |
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers 2 and −2 are the same distance from zero, they are called opposites. The opposite of 2 is −2, and the opposite of −2 is 2.
Opposite
The Opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
![Rendered by QuickLaTeX.com \[\LARGE{ \begin{center} \;{\color{mypurple1}\overbrace{\quad\quad\quad\quad\quad\quad\quad }}^{3}\:\color{mypurple1}\overbrace{\; \quad \quad\quad\quad\quad\quad }}^{3}\\ \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{-4 \quad {\color{mypurple1}-3} \quad -2 \quad -1\quad {0 \quad 1 \quad 2 \quad {\color{mypurple1}3} \quad 4} \\ \textit{\caption{The opposite of 3 is −3.}} \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-77b41b729dc187c108063fcb45f869bc_l3.png)
Sometimes in algebra, the same symbol has different meanings. Just like some words in English, the specific meaning becomes clear by looking at how it is used. You have seen the symbol “-” used in three different ways. We demonstrate four examples in the table below.
| Expression |
Explanation |
| 10 − 4 | Between two numbers, it indicates the operation of subtraction. We read 10−4 as “10 minus 4.” |
| −8 | In front of a number, it indicates a negative number. We read −8 as “negative eight.” |
| −x | In front of a variable, it indicates the opposite. We read −x as “the opposite of x.” |
| −(−2) | Here there are two “−” signs. The one in the parentheses tells us the number is negative 2. The one outside the parentheses tells us to take the opposite of −2. We read −(−2) as “the opposite of negative two.” |
Try it!
Find:
a. the opposite of 7
b. the opposite of −10
c. −(−6).
Solution (click to reveal)
| Translation |
Algebraic |
| a. −7 is the same distance from 0 as 7, but on the opposite side of 0. |
The opposite of 7 is −7. |
| b. 10 is the same distance from 0 as −10, but on the opposite side of 0. |
The opposite of −10 is 10. |
| c. −(−6) |
The opposite of −(−6) is −6. |
Our work with opposites gives us a way to define the integers. The whole numbers and their opposites are called the integers. The integers are the numbers …−3, −2, −1, 0, 1, 2, 3…
Integers
…−3, −2, −1, 0, 1, 2, 3…
When evaluating the opposite of a variable, we must be very careful. Without knowing whether the variable represents a positive or negative number, we don’t know whether −x is positive or negative. We can see this in the example below.
Try it!
Evaluate:
a. −x, when x = 8
b. −x, when x = −8.
Solution A (click to reveal)
a. To evaluate when x = 8 means to substitute ![]() for x.
for x.
| Steps | Algebraic |
| Example | −x |
| Substitute |
−( |
| Write the opposite of 8. | −8 |
Solution B (click to reveal)
b. To evaluate when x = −8 means to substitute ![]() for x.
for x.
| Steps | Algebraic |
| Example | −x |
| Substitute |
−( |
| Write the opposite of -8. | 8 |
Add and Subtract Integers
So far, we have only used counting numbers and whole numbers.
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more challenging.
We will use two color counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
We let one color (blue) represent positive. The other color (orange) will represent the negatives.

If we have one positive counter and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero.
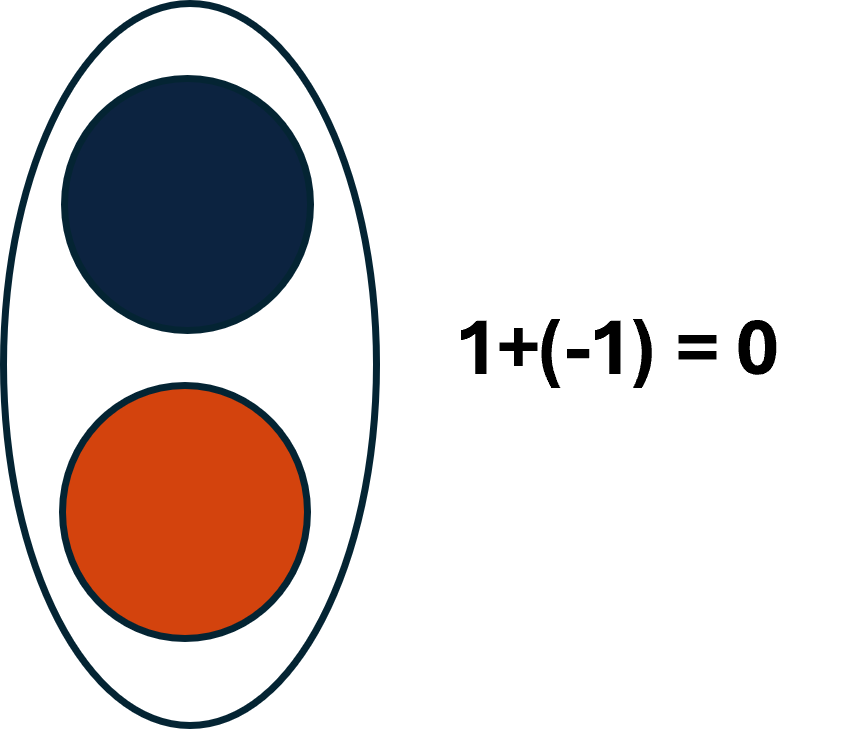
We will use the counters to show how to add:
a. 5 + 3,
b. −5 + (−3),
c. −5 + 3,
d. 5 + (−3)
The first example, 5 + 3, adds 5 positives and 3 positives—both positives.
The second example, −5 + (−3), adds 5 negatives and 3 negatives—both negatives.
When the signs are the same, the counters are all the same color, and so we add them. In each case we get 8—either 8 positives or 8 negatives.

So what happens when the signs are different? Let’s add −5 + 3 and 5 + (−3).
When we use counters to model addition of positive and negative integers, it is easy to see whether there are more positive or more negative counters. So we know whether the sum will be positive or negative.
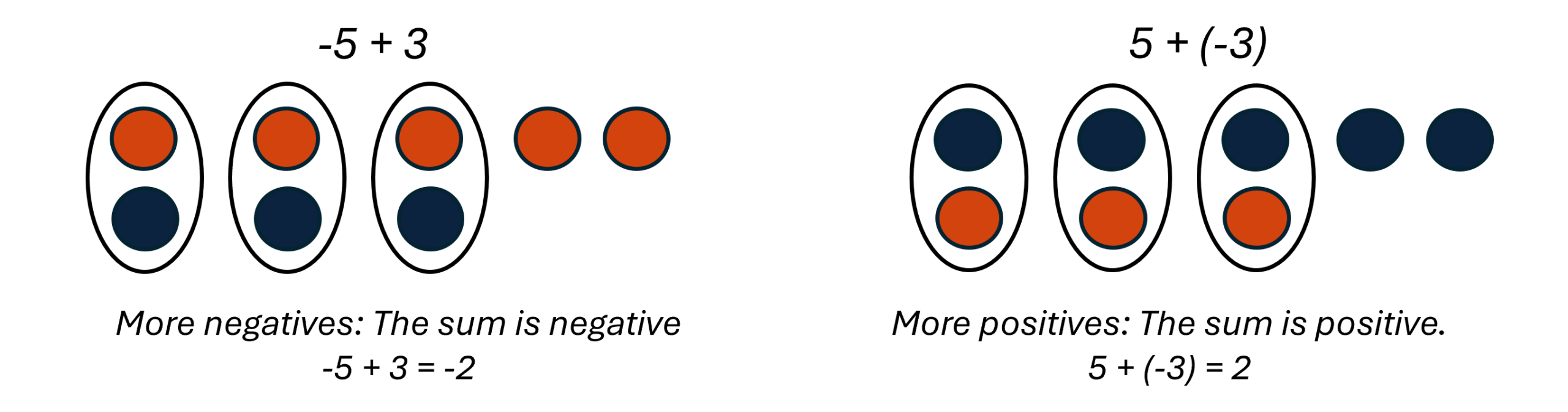
Try it!
Add:
a. −1 + (−4)
b. −1 + 5
c. 1 + (−5).
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Original example | −1 +(−4) |
| Show counters |  |
| 1 negative plus 4 negatives is 5 negatives | -5 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Original example | −1 + 5 |
| Show counters |  |
| There are more positives, so the sum is positive. | 4 |
Solution C (click to reveal)
c.
| Steps | Algebraic |
| Original example | 1 + (−5) |
| Show counters |  |
| There are more negatives, so the sum is negative. | -4 |
We will continue to use counters to model the subtraction. Perhaps when you were younger, you read “5 − 3” as “5 take away 3.” When you use counters, you can think of subtraction the same way!
We will use the counters to show how to subtract in the table below:
| Ex. 1 | Ex. 2 | Ex. 3 | Ex. 4 |
| 5 – 3 | −5 – (−3) | −5 – 3 | 5 – (−3) |
The first example, 5 − 3 we subtract 3 positives from 5 positives and end up with 2 positives.
In the second example, −5 − (−3), we subtract 3 negatives from 5 negatives and end up with 2 negatives.
Each example used counters of only one color, and the “take away” model of subtraction was easy to apply.

What happens when we have to subtract one positive and one negative number? We’ll need to use both blue and orange counters as well as some neutral pairs. If we don’t have the number of counters needed to take away, we add neutral pairs. Adding a neutral pair does not change the value. It is like changing quarters to nickels—the value is the same, but it looks different.
Let’s look at −5 − 3 and 5 − (−3) in the table below.
| Steps | Ex. 1 | Ex. 2 |
| Examples | −5 − 3 | 5 − (−3) |
| Model the first number. | ||
| We now add the needed neutral pairs. |  |
 |
| We remove the number of counters modeled by the second number. |  |
 |
| Count what is left. |  |
 |
| Translate it | −5 − 3 = -8 | 5 − (−3) = 8 |
| Simplify | -8 | 8 |
Try it!
Subtract: a. 3 − 1 b. −3 − (−1) c. −3 − 1 d. 3 − (−1).
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Original problem | 3 – 1 |
| Show counter |  |
| Take 1 positive from 3 positives and get 2 positives. | 2 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Original problem | −3 − (−1) |
| Show counter |  |
| Take 1 positive from 3 negatives and get 2 negatives. | -2 |
Solution C (click to reveal)
c.
| Steps | Algebraic |
| Original problem | −3 − 1 |
| Counters |  |
| Take 1 positive from the one added neutral pair. |  |
| Solution | -4 |
Solution D (click to reveal)
d.
| Steps | Algebraic |
| Original example | 3 − (−1) |
| Counters |  |
| Take 1 negative from the one added neutral pair. |  |
| Solution | 4 |
Have you noticed that subtraction of signed numbers can be done by adding the opposite? In the last example, −3 −1 is the same as −3 + (−1) and 3 − (−1) is the same as 3 + 1. You will often see this idea, the Subtraction Property, written as follows:
Try it!
Simplify: a.
13 − 8 and 13 + (−8)
b. −17 − 9 and −17 + (−9)
c. 9 − (−15) and 9 + 15
d. −7 − (−4) and −7 + 4.
Solution A (click to reveal)
a.
| Steps | Ex. 1 | Ex. 2 |
| Example | 13 − 8 | 13 + (−8) |
| Subtract. | 5 | 5 |
Solution B (click to reveal)
b.
| Steps | Ex. 1 | Ex. 2 |
| Example | −17 − 9 | −17 + (−9) |
| Subtract. | −26 | −26 |
Solution C (click to reveal)
c.
| Steps | Ex. 1 | Ex. 2 |
| Example | 9 − (−15) | 9 + 15 |
| Subtract. | 24 | 24 |
Solution D (click to reveal)
d.
| Steps | Ex. 1 | Ex. 2 |
| Example | −7 − (−4) | −7 + 4 |
| Subtract. | −3 | −3 |
Try it!
Simplify: 7 − (−4 − 3) − 9
Solution (click to reveal)
| Steps | Algebraic |
| Example | 7 − (−4 − 3) − 9 |
| Simplify inside the parentheses first. | 7 − (−7) − 9 |
| Subtract left to right. | 14 − 9 |
| Subtract | 5 |
Multiply and Divide Integers
Since multiplication is mathematical shorthand for repeated addition, our model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction. Here, we will use the model just to help us discover the pattern.
We remember that a · b means add a, b times. Here, we are using the model just to help us discover the pattern.
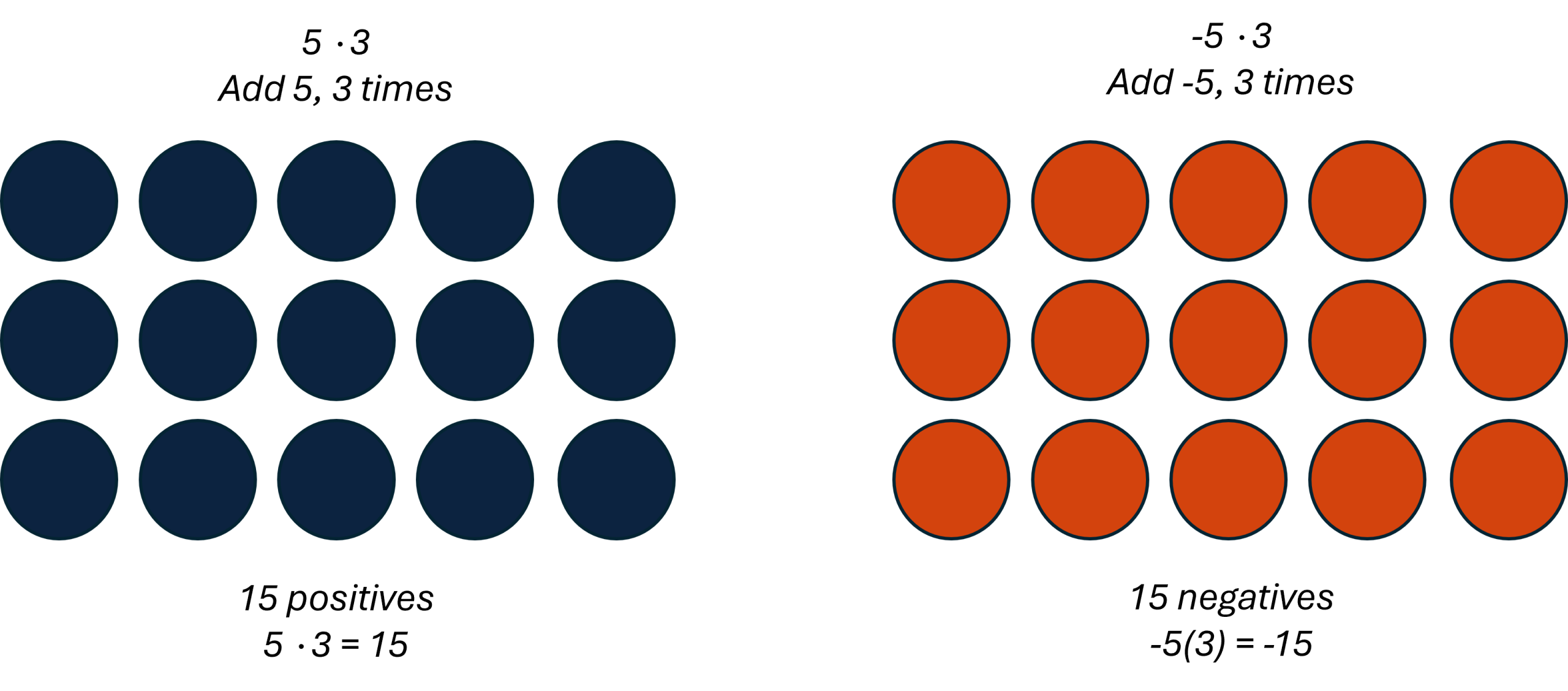 The next two examples are more interesting. What does it mean to multiply 5 by -3? It means subtract 5, 3 times. Looking at subtraction as “taking away,” it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the workspace.
The next two examples are more interesting. What does it mean to multiply 5 by -3? It means subtract 5, 3 times. Looking at subtraction as “taking away,” it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the workspace.
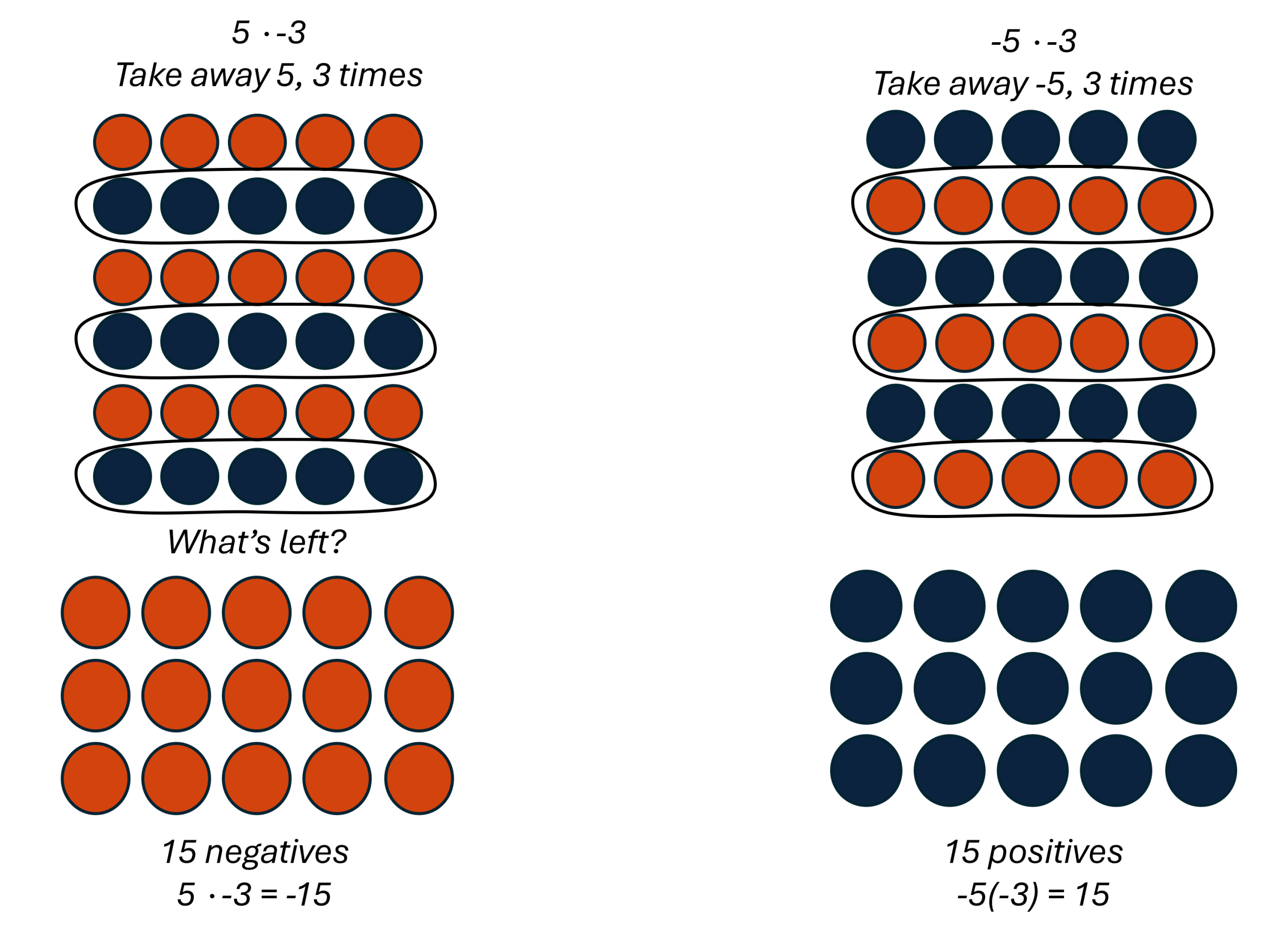
The table below summarizes these steps in equation form:
| Ex. 1 | Ex. 2 |
| 5 · 3 = 15 | −5(3) = −15 |
| 5(−3) = −15 | (−5)(−3) = 15 |
The table below draws attention to two important rules for the multiplication of two signed numbers:
| Rules |
| signs are the same, the product is positive. |
| signs are different, the product is negative. |
What about division? Division is the inverse operation of multiplication. So, 15 ÷ 3 = 5 because 5 · 3 = 15. In words, this expression says that 15 can be divided into 3 groups of 5 each because adding five three times gives 15. If you look at some examples of multiplying integers in the table below, you can see the rules for dividing integers.
| Ex. 1 | Ex. 2 |
| 5 · 3 = 15 so 15 ÷ 3 = 5 | −5 (3) = −15 so −15 ÷ 3 = −5 |
| (−5)(−3) = 15 so 15 ÷ (−3) = −5 | 5(−3) = −15 so −15 ÷ (−3) = 5 |
Division follows the same rules as multiplication with regard to signs.
Multiplication of Signed Numbers
See the tables below for multiplication of two signed numbers:
| Same signs | Product | Example |
|---|---|---|
| Two positives |
Positive |
7 · 4 = 28 |
| Two negatives | Positive | −8(−6) = 48 |
| Different signs | Product | Example |
|---|---|---|
| Positive · negative |
Negative |
7(−9) = −63 |
| Negative · positive | Negative | −5 · 10 = −50 |
Try it!
Multiply or divide: a. −100 ÷ (−4) b. 7 · 6 c. 4(−8) d. –27 ÷ 3.
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Example | −100 ÷ (−4) |
| Divide, with signs that are the same the quotient is positive. | 25 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Example | 7 · 6 |
| Multiply, with same signs | 42 |
Solution C (click to reveal)
c.
| Steps | Algebraic |
| Example | 4(−8) |
| Multiply, with different signs. | −32 |
Solution D (click to reveal)
d.
| Steps | Algebraic |
| Example | −27 ÷ 3 |
| Divide, with different signs, the quotient is negative. | −9 |
When we multiply a number by 1, the result is the same number. What happens when we multiply a number by −1? Let’s multiply a positive number and then a negative number by −1 to see what we get in the table below.
| Steps | Ex. 1 | Ex. 2 |
| Example | −1 · 4 | −1(−3) |
| Multiply. | -4 | 3 |
| Solution | −4 is the opposite of 4. | 3 is the opposite of −3. |
Each time we multiply a number by −1, we get its opposite!
Multiplication by −1
Multiplying a number by −1 gives its opposite.
Try it!
Multiply: a. -1 ![]() 7 b. -1(-11)
7 b. -1(-11)
Solution (click to reveal)
| Steps | Algebraic |
| a. Multiply, noting that the signs are different so the product is negative. | −1 · 7 |
| Simplify | -7 |
| Solution | -7 is the opposite of 7. |
| b. Multiply, noting that the signs are the same so the product is positive. |
−1(−11) |
| Simplify | 11 |
| Solution | 11 is the opposite of −11. |
Identify Multiples of a Number
The numbers 2, 4, 6, 8, 10, 12 are called multiples of 2. A multiple of 2 can be written as the product of a counting number and 2.
Multiples of 2:
![]()
Similarly, a multiple of 3 would be the product of a counting number and 3.
Multiples of 3:
![]()
We could find the multiples of any number by continuing this process in the table below.
| Counting Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Multiples of 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Multiples of 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Multiples of 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Multiples of 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Multiples of 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Multiples of 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Multiples of 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Multiples of 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
Multiple of a Number
A number is a multiple of n if it is the product of a counting number and n.
Another way to say that 15 is a multiple of 3 is to say that 15 is divisible by 3. That means that when we divide 3 into 15, we get a counting number. In fact, 15 ÷ 3 is 5, so 15 is 5 · 3.
Use Common Divisibility Tests
Another way to say that 375 is a multiple of 5 is to say that 375 is divisible by 5. In fact, 375 ÷ 5 is 75, so 375 is 5 ⋅ 75. However, 10,519 is not a multiple of 3. When we divide 10,519 by 3 we do not get a counting number, so 10,519 is not divisible by 3.
Divisibility
If a number m is a multiple of n, then we say that m is divisible by n.
Since multiplication and division are inverse operations, the patterns of multiples that we found can be used as divisibility tests. The table below summarizes divisibility tests for some of the counting numbers between one and ten.
| A number is divisible by | Description |
| 2 | if the last digit is 0, 2, 4, 6, or 8 |
| 3 | if the sum of the digits is divisible by 3 |
| 5 | if the last digit is 5 or 0 |
| 6 | if divisible by both 2 and 3 |
| 10 | if the last digit is 0 |
Try it!
Determine whether 1,290 is divisible by 2, 3, 5, and 10.
Solution (click to reveal)
The table applies the divisibility tests to 1,290. In the far right column, we check the results of the divisibility tests by seeing if the quotient is a whole number.
| Divisible by…? | Test | Divisible? | Check |
|---|---|---|---|
| 2 | Is last digit 0, 2, 4, 6, or 8? Yes. | yes | 1290 ÷ 2 = 645 |
| 3 | Is sum of digits divisible by 3? 1 + 2 + 9 + 0 = 12 Yes. |
yes | 1290 ÷ 3 = 430 |
| 5 | Is last digit 5 or 0? Yes. | yes | 1290 ÷ 5 = 258 |
| 10 | Is last digit 0? Yes. | yes | 1290 ÷ 10 = 129 |
Thus, 1,290 is divisible by 2, 3, 5, and 10.
Determine whether 5,625 is divisible by 2, 3, 5, and 10.
Solution (click to reveal)
The table applies the divisibility tests to 5,625 and tests the results by finding the quotients.
| Divisible by…? | Test | Divisible? | Check |
|---|---|---|---|
| 2 | Is last digit 0, 2, 4, 6, or 8? No. | no | 5625 ÷ 2 = 2812.5 |
| 3 | Is sum of digits divisible by 3?
5 + 6 + 2 + 5 = 18 Yes. |
yes | 5625 ÷ 3 = 1875 |
| 5 | Is last digit 5 or 0? Yes. | yes | 5625 ÷ 5 = 1125 |
| 10 | Is last digit 0? No. | no | 5625 ÷ 10 = 562.5 |
Thus, 5,625 is divisible by 3 and 5, but not 2, or 10.
Find all the Factors of the Given Number
There are often several ways to talk about the same idea. So far, we’ve seen that if m is a multiple of n, we can say that m is divisible by n. We know that 72 is the product of 8 and 9, so we can say 72 is a multiple of 8 and 72 is a multiple of 9. We can also say 72 is divisible by 8 and by 9. Another way to talk about this is to say that 8 and 9 are factors of 72. When we write 72 = 8 ⋅ 9 we can say that we have factored 72.
![]()
Factors
If a ⋅ b = m, then a and b are factors of m, and m is the product of a and b.
In algebra, it can be useful to determine all of the factors of a number. This is called factoring a number, and it can help us solve many kinds of problems.
For example, suppose a choreographer is planning a dance for a ballet recital. There are 24 dancers, and for a certain scene, the choreographer wants to arrange the dancers in groups of equal sizes on stage.
In how many ways can the dancers be put into groups of equal size? Answering this question is the same as identifying the factors of 24. The table below summarizes the different ways that the choreographer can arrange the dancers.
| Number of Groups | Dancers per Group | Total Dancers |
|---|---|---|
| 1 | 24 | 1 ⋅ 24 = 24 |
| 2 | 12 | 2 ⋅ 12 = 24 |
| 3 | 8 | 3⋅ 8 = 24 |
| 4 | 6 | 4 ⋅ 6 = 24 |
| 6 | 4 | 6 ⋅ 4 = 24 |
| 8 | 3 | 8 ⋅ 3 = 24 |
| 12 | 2 | 12 ⋅ 2 = 24 |
| 24 | 1 | 24 ⋅ 1 = 24 |
What patterns do you see in the table? Did you notice that the number of groups times the number of dancers per group is always 24? This makes sense, since there are always 24 dancers.
You may notice another pattern if you look carefully at the first two columns. These two columns contain the exact same set of numbers—but in reverse order. They are mirrors of one another, and in fact, both columns list all of the factors of 24, which are:
We can find all the factors of any counting number by systematically dividing the number by each counting number, starting with 1. If the quotient is also a counting number, then the divisor and the quotient are factors of the number. We can stop when the quotient becomes smaller than the divisor.
How to find all the factors of a counting number.
- Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
- If the quotient is a counting number, the divisor and quotient are a pair of factors.
- If the quotient is not a counting number, the divisor is not a factor.
- List all the factor pairs.
- Write all the factors in order from smallest to largest.
Try it!
Find all the factors of 72.
Solution (click to reveal)
Divide 72 by each of the counting numbers starting with 1. If the quotient is a whole number, the divisor and quotient are a pair of factors.
| Dividend | Divisor | Quotient | Factors |
|---|---|---|---|
| 72 | 1 | 72 | 1, 72 |
| 72 | 2 | 36 | 2, 36 |
| 72 | 3 | 24 | 3, 24 |
| 72 | 4 | 18 | 4, 18 |
| 72 | 5 | 14.4 | – |
| 72 | 6 | 12 | 6, 12 |
| 72 | 7 | ~10.29 | – |
| 72 | 8 | 9 | 8, 9 |
The next line would have a divisor of 9 and a quotient of 8. The quotient would be smaller than the divisor, so we stop. If we continued, we would end up only listing the same factors again in reverse order. Listing all the factors from smallest to greatest, we have
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72
Key Concepts
| Operation | Notation | Say: | The result is… |
|---|---|---|---|
| Addition | a + b | a plus b | the sum of a and b |
| Subtraction | a − b | a minus b | the difference of a and b |
| Multiplication | a·b, (a)(b), (a)b, a(b) | a times b | The product of a and b |
| Division | a ÷ b, a/b, |
a divided by b | The quotient of a and b |
- Equality Symbol:
- a = b is read a is equal to b
- The symbol = is called the equal sign.
- Inequality
| Visual of line graph |
Translation of graph |
|---|---|
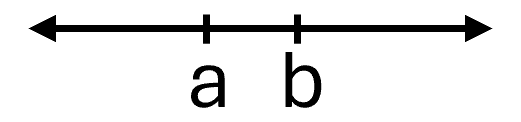 |
|
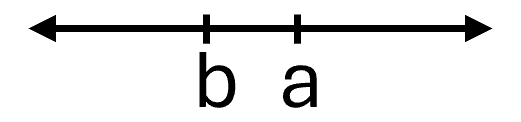 |
|
| Algebraic Notation | Say |
|---|---|
| a = b | a is equal to b |
| a ≠ b | a is not equal to b |
| a < b | a is less than b |
| a > b | a is greater than b |
| a ≤ b | a is less than or equal to b |
| a ≥ b | a is greater than or equal to b |
- Subtraction Property: Subtracting a number is the same as adding its opposite.
| A number is divisible by | Description |
| 2 | if the last digit is 0, 2, 4, 6, or 8 |
| 3 | if the sum of the digits is divisible by 3 |
| 5 | if the last digit is 5 or 0 |
| 6 | if divisible by both 2 and 3 |
| 10 | if the last digit is 0 |
- Factors If a ⋅ b = m, then a and b are factors of m, and m is the product of a and b.
- Find all the factors of a counting number.
- Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
- If the quotient is a counting number, the divisor and quotient are a pair of factors.
- If the quotient is not a counting number, the divisor is not a factor.
- List all the factor pairs.
- Write all the factors in order from smallest to largest.
- Divide the number by each of the counting numbers, in order, until the quotient is smaller than the divisor.
- Determine if a number is prime.
- Test each of the primes, in order, to see if it is a factor of the number.
- Start with 2 and stop when the quotient is smaller than the divisor or when a prime factor is found.
- If the number has a prime factor, then it is a composite number. If it has no prime factors, then the number is prime.
- Derived from Openstax Intermediate Algebra, Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction . Pre-algebra, Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction. Elementary Algebra, Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction . ↵
Counting numbers start with 1 and continue.

![Rendered by QuickLaTeX.com \[\LARGE{ \begin{center} \;{\color{mypurple1}\overbrace{\quad\quad\quad\quad\quad\quad }}^{7}\:\color{mypurple1}\overbrace{\quad \quad\quad\quad\quad\quad }}^{7}\\ \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{ {\color{mypurple1}-7}\quad\quad \quad \quad \quad 0 \quad \quad \quad \quad\quad{\color{mypurple1}7} } \\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-20ecc89f4dd13b13f7133cc858dbe4cd_l3.png)
![Rendered by QuickLaTeX.com \[\LARGE{ \begin{center} \;{\color{mypurple1}\overbrace{\quad\quad\quad\quad\quad\quad }}^{10}\:\color{mypurple1}\overbrace{\quad \quad\quad\quad\quad\quad }}^{10}\\ \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{ {\color{mypurple1}-10}\quad\quad \quad \quad \quad 0 \quad \quad \quad \quad\quad{\color{mypurple1}10} } \\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-58eb16e4c60c83c234a9015aae6f3ba3_l3.png)
![Rendered by QuickLaTeX.com \[\LARGE{ \begin{center} \;{\color{mypurple1}\overbrace{\quad\quad\quad\quad\quad\quad }}^{6}\:\color{mypurple1}\overbrace{\quad \quad\quad\quad\quad\quad }}^{6}\\ \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{ {\color{mypurple1}-6}\quad\quad \quad \quad \quad 0 \quad \quad \quad \quad\quad{\color{mypurple1}6} } \\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2c00f694283066653adfa4ff36ffcb21_l3.png)
