23 Factoring Polynomials
Learning Objectives
Greatest Common Factor of a Polynomial
We have learned how to factor numbers to find the least common multiple (LCM) of two or more numbers. Now we will factor expressions and find the greatest common factor of two or more expressions. The method we use is similar to what we used to find the LCM.
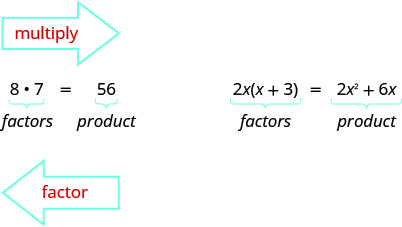
Greatest Common Factor
The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.
Try it!
Find the greatest common factor of 21x3, 9x2, 15x.
| Steps | Algebraic |
| Factor each coefficient into primes and write the variables with exponents in expanded form. Circle the common factors in each column. Bring down the common factors. |
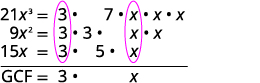 |
| Multiply the factors. | The GCF of 21x3, 9x2 and 15x is 3x. |
When we study fractions, we learn that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance, 4 is the GCF of 16 and 20 because it is the largest number that divides evenly into both 16 and 20. The GCF of polynomials works the same way: 4x is the GCF of 16x and 20x2 because it is the largest polynomial that divides evenly into both 16x and 20x2.
When factoring a polynomial expression, our first step should be to check for a GCF. Look for the GCF of the coefficients, and then look for the GCF of the variables.
Greatest Common Factor
The greatest common factor (GCF) of polynomials is the largest polynomial that divides evenly into the polynomials.
Given a polynomial expression, factor out the greatest common factor.
- Identify the GCF of the coefficients.
- Identify the GCF of the variables.
- Combine to find the GCF of the expression.
- Determine what the GCF needs to be multiplied by to obtain each term in the expression.
- Write the factored expression as the product of the GCF and the sum of the terms we need to multiply by.
We state the Distributive Property here just as you saw it in earlier chapters and “in reverse.”
Distributive Property
If a, b, and c are real numbers, then
The form on the left is used to multiply. The form on the right is used to factor.
So how do you use the Distributive Property to factor a polynomial? You just find the GCF of all the terms and write the polynomial as a product!
Try it! – How to Use the Distributive Property to factor a polynomial




Try it! – Factoring the Greatest Common Factor
Factor: 6x3y3 + 45x2y2 + 21xy.
Solution
| Steps | Algebraic |
| First, find the GCF of the expression. (Note that the GCF of a set of expressions in the form xn will always be the exponent of lowest degree.) | The GCF of 6, 45 and 21 is 3.
The GCF of x3, x2, and x is x. And the GCF of y3, y2, and y is y. |
| Combine these to find the GCF of the polynomial, | GCF = 3xy |
| Next, determine what the GCF needs to be multiplied by to obtain each term of the polynomial. | We find that 3xy(2x2y2) = 6x3y3, 3xy(15xy) = 45x2y2, and 3xy(7) = 21xy. |
| Finally, write the factored expression as the product of the GCF and the sum of the terms we needed to multiply by. | (3xy)(2x2y2 + 15xy + 7) |
After factoring, we can check our work by multiplying. Use the distributive property to confirm that (3xy)(2x2y2 + 15xy + 7) = 6x3y3 + 45x2y2 + 21xy.
Try it!
Factor x(b2 – a) + 6(b2 – a) by pulling out the GCF.
Solution
(b2 – a)(x + 6)
Factor by Grouping
Sometimes there is no common factor of all the terms of a polynomial. When there are four terms we separate the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts. Not all polynomials can be factored. Just like some numbers are prime, some polynomials are prime.
Try it! – How to Factor a Polynomial by Grouping




- Group terms with common factors.
- Factor out the common factor in each group.
- Factor the common factor from the expression.
- Check by multiplying the factors.
Try it!
Factor by grouping: a. x2 + 3x − 2x − 6 b. 6x2 − 3x − 4x + 2.
Solution
a.
| Steps | Algebraic |
| First, find the GCF of the expression. (Note that the GCF of a set of expressions in the form xn will always be the exponent of lowest degree.) | There is no GCF in all four terms. |
| Separate into two parts. | x2 + 3x , −2x − 6 |
| Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms. | x(x + 3) − 2(x + 3) |
| Factor out the common factor. | (x + 3)(x − 2) |
Check on your own by multiplying.
b.
| Steps | Algebraic |
| First, find the GCF of the expression. (Note that the GCF of a set of expressions in the form xn will always be the exponent of lowest degree.) | There is no GCF in all four terms. |
| Separate into two parts. | 6x2 − 3x −4x + 2 |
| Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms. | 3x(2x − 1) −2(2x − 1) |
| Factor out the common factor. | (2x − 1)(3x − 2) |
Check on your own by multiplying.
Factor Trinomials
Does the order of the factors matter?
No. Multiplication is commutative, so the order of the factors does not matter.
You have already learned how to multiply binomials using FOIL. Now you’ll need to “undo” this multiplication. To factor the trinomial means to start with the product, and end with the factors.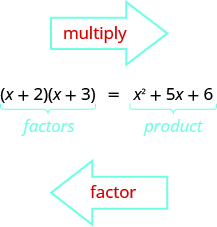 To figure out how we would factor a trinomial of the form x2 + bx + c, such as x2 + 5x + 6 and factor it to (x + 2)(x + 3), let’s start with two general binomials of the form (x + m) and (x + n).
To figure out how we would factor a trinomial of the form x2 + bx + c, such as x2 + 5x + 6 and factor it to (x + 2)(x + 3), let’s start with two general binomials of the form (x + m) and (x + n).
| Steps | Algebraic |
| Example | |
| Foil to find the product. | |
| Factor the GCF from the middle terms. | |
| Our trinomial is of the form x2 + bx + c. |
This tells us that to factor a trinomial of the form x2 + bx + c, we need two factors (x + m) and (x + n) where the two numbers m and n multiply to c and add to b.
Try i1! – How to Factor a Trinomial of the form x2+bx+c
Factor: x2 + 11x + 24.
Solution




Let’s summarize the method we just developed to factor trinomials of the form x2 + bx + c.
Strategy for Factoring Trinomials of the Form x2 + bx + c
When we factor a trinomial, we look at the signs of its terms first to determine the signs of the binomial factors.
Notice that, in the case when m and n have opposite signs, the sign of the one with the larger absolute value matches the sign of b.
What happens when the leading coefficient is not 1 and there is no GCF? There are several methods that can be used to factor these trinomials. First we will use the Trial and Error method.
Let’s factor the trinomial 3×2 + 5x + 2.
From our earlier work, we expect this will factor into two binomials.
3x2 + 5x + 2
(____)(____)
We know the first terms of the binomial factors will multiply to give us 3x2. The only factors of 3x2 are 1x, 3x. We can place them in the binomials.
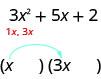 Check: Does 1x · 3x = 3x2?
Check: Does 1x · 3x = 3x2?
We know the last terms of the binomials will multiply to 2. Since this trinomial has all positive terms, we only need to consider positive factors. The only factors of 2 are 1, 2. But we now have two cases to consider as it will make a difference if we write 1, 2 or 2, 1.
 Which factors are correct? To decide that, we multiply the inner and outer terms.
Which factors are correct? To decide that, we multiply the inner and outer terms.
 Since the middle term of the trinomial is 5x, the factors in the first case will work. Let’s use FOIL to check.
Since the middle term of the trinomial is 5x, the factors in the first case will work. Let’s use FOIL to check.
Our result of the factoring is:
Try it! – How to Factor a Trinomial Using Trial and Error
Factor completely using trial and error: 3y2 + 22y + 7.
Solution






Factor trinomials of the form ax2 + bx + c using trial and error.
- Write the trinomial in descending order of degrees as needed.
- Factor any GCF.
- Find all the factor pairs of the first term.
- Find all the factor pairs of the third term.
- Test all the possible combinations of the factors until the correct product is found.
- Check by multiplying.
Remember, when the middle term is negative and the last term is positive, the signs in the binomials must both be negative.
Try it!
Factor completely using trial and error: 6b2 − 13b + 5.
Solution
| Steps | Algebraic |
| The trinomial is already in descending order. | |
| Find the factors of the first term. | |
| Find the factors of the last term. Consider the signs. Since the last term, 5, is positive its factors must both be positive or both be negative. The coefficient of the middle term is negative, so we use the negative factors. |
Consider all the combinations of factors.
| Example | |
| 6b2 − 13b + 5 | |
| Possible factors | Product |
| (b − 1)(6b − 5) | 6b2 − 11b + 5 |
| (b − 5)(6b − 1) | 6b2 − 31b + 5 |
| (2b − 1)(3b − 5) | 6b2 − 13b + 5* |
| (2b − 5)(3b − 1) | 6b2 − 17b + 5 |
The correct factors are those whose product is the original trinomial. (2b − 1)(3b − 5)
Check by multiplying:
(2b − 1)(3b − 5)
6b2 − 10b − 3b + 5
6b2 − 13b + 5 ✓
When we factor an expression, we always look for a greatest common factor first. If the expression does not have a greatest common factor, there cannot be one in its factors either. This may help us eliminate some of the possible factor combinations.
Try it!
Factor completely using trial and error: 18x2 − 37xy + 15y2.
Solution
| Steps | Algebraic |
| The trinomial is already in descending order. | |
| Find the factors of the first term. | 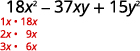 |
| Find the factors of the last term. Consider the signs. Since 15 is positive and the coefficient of the middle term is negative, we use the negative factors. |
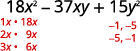 |
Consider all the combinations of factors.

The correct factors are those whose product is the original trinomial.
(2x − 3y)(9x − 5y)
Check by multiplying:
(2x − 3y)(9x − 5y)
18x2 − 10xy − 27xy + 15y2
18x2 − 37xy + 15y2
Don’t forget to look for a GCF first and remember if the leading coefficient is negative, so is the GCF.
Try it!
Factor completely using trial and error: −10y4 − 55y3 − 60y2.
Solution
| Steps | Algebraic |
| Example | |
| Notice the greatest common factor, so factor it first. | |
| Factor the trinomial. | 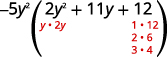 |
Consider all the combinations.
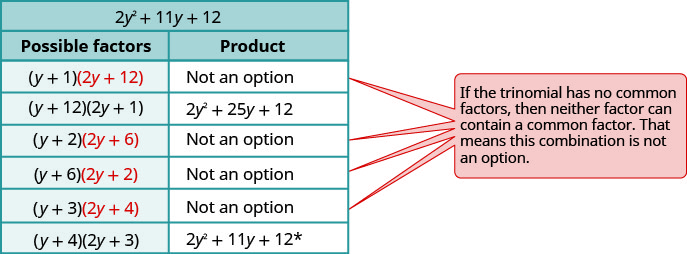
The correct factors are those whose product is the original trinomial. Remember to include the factor −5y2.
−5y2(y + 4)(2y + 3)
Check by multiplying:
−5y2(y + 4)(2y + 3)
−5y2(2y2 + 8y + 3y + 12)
−10y4 − 55y3 − 60y2 ✓
Factor Difference of Squares
Do you remember the Difference of Squares from the last module? A difference of squares is a perfect square subtracted from a perfect square. Recall that a difference of squares can be rewritten as factors containing the same terms but opposite signs because the middle terms cancel each other out when the two factors are multiplied.
A difference of squares can be rewritten as two factors containing the same terms but opposite signs.
Step 1. Does the binomial fit the pattern? a2 − b2
Is this a difference? ____−____
Are the first and last terms perfect squares?
Step 2. Write them as squares. (a)2 − (b)2
Step 3. Write the product of conjugates. (a − b)(a + b)
Step 4. Check by multiplying.
Try it!
Factor: 144x2 − 49y2.
Solution
| Steps | Algebraic |
| Example | 144x2 − 49y2 |
| Is this a difference of squares? Yes. | (12x)2 − (7y)2 |
| Factor as the product of conjugates. | (12x − 7y)(12x + 7y) |
| Check by multiplying. | (12x − 7y)(12x + 7y)
144x2 − 49y2 ✓ |
Try it! – Factoring a Difference of Squares
Factor 9x2 − 25.
Solution
Notice that 9x2 and 25 are perfect squares because 9x2 = (3x)2 and 25 = 52. The polynomial represents a difference of squares and can be rewritten as (3x +5)(3x − 5).
As always, you should look for a common factor first whenever you have an expression to factor. Sometimes a common factor may “disguise” the difference of squares and you won’t recognize the perfect squares until you factor the GCF.
Try it!
Factor: 48x4y2 − 243y2.
Solution
| Steps | Algebraic |
| Example | 48x4y2 − 243y2 |
| Is there a GCF? Yes, 3y2—factor it out! | 3y2(16x4 − 81) |
| Is the binomial a difference of squares? Yes. | 3y2((4x2)2 − (9)2) |
| Factor as a product of conjugates. | 3y2(4x2 − 9)(4x2 + 9) |
| Notice the first binomial is also a difference of squares! | 3y2((2x)2 − (3)2)(4x2 + 9) |
| Factor it as the product of conjugates. The last factor, the sum of squares, cannot be factored. | 3y2(2x − 3)(2x + 3)(4x2 + 9) |
| Check by multiplying: | 3y2(2x − 3)(2x + 3)(4x2 + 9)
3y2(4x2 − 9)(4x2 + 9) 3y2(16x4 − 81) 48x4y2 − 243y2✓ |
Factoring a Perfect Square Trinomial
Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter.
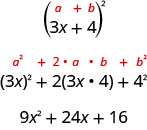
Perfect Square Trinomials
a2 + 2ab + b2 = (a + b)2
and
a2 − 2ab + b2 = (a − b)2
We can use this equation to factor any perfect square trinomial.
Step 1. Does the trinomial fit the pattern? a2 + 2ab + b2 a2 – 2ab + b2
Is the first term a perfect square? (a)2 (b)2
Write it as a square.
Is the last term a perfect square? (a)2 (b)2 (a)2 (b)2
Write it as a square.
Check the middle term. Is it 2ab? (a)2 ↘2 · a · b↙ (b)2 (a)2 ↘2 · a · b↙ (b)2
Step 2. Write the square of the binomial. (a + b)2 (a − b)2
Step 3. Check by multiplying.
Try it!
Factor: 9×2 + 12x + 4.
Solution



Try it! – Factoring a Perfect Square Trinomial
Factor: 25x2 + 20x + 4.
Solution
Notice that 25x2 and 4 are perfect squares because 25x2 = (5x)2 and 4 = 22. Then check to see if the middle term is twice the product of 5x and 2. The middle term is, indeed, twice the product: 2(5x)(2) = 20x. Therefore, the trinomial is a perfect square trinomial and can be written as (5x+2)2.
Try it!
Factor: 81y2 − 72y + 16.
Solution
The first and last terms are squares. See if the middle term fits the pattern of a perfect square trinomial. The middle term is negative, so the binomial square would be (a − b)2.
| Steps | Algebraic |
| Example | |
| Are the first and last terms perfect squares? | |
| Check the middle term. | 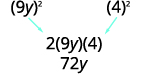 |
| Does it match (a−b)2? Yes. | |
| Write as the square of a binomial. | |
| Check by multiplying: |
(9y − 4)2(9y)2 − 2 · 9y · 4 + 42
81y2 − 72y + 16 ✓ |
Factoring the Sum and Difference of Cubes
Now, we will look at two new special products: the sum and difference of cubes. Although the sum of squares cannot be factored, the sum of cubes can be factored into a binomial and a trinomial.
We can use the acronym SOAP to remember the signs when factoring the sum or difference of cubes. The first letter of each word relates to the signs: Same Opposite Always Positive. For example, consider the following example.
The sign of the first 2 is the same as the sign between x3 − 23. The sign of the 2x term is opposite the sign between x3 − 23. And the sign of the last term, 4, is always positive.
We can factor the sum of two cubes as
We can factor the difference of two cubes as
We’ll check the first pattern and leave the second to you.
| Steps | Algebraic |
| Example | |
| Distribute. | |
| Multiply. | |
| Combine like terms. |
Given a sum of cubes or difference of cubes, factor it.
- Confirm that the first and last term are cubes,
a3 + b3 or a3 − b3. - For a sum of cubes, write the factored form as
(a + b)(a2 − ab + b2). For a difference of cubes, write the factored form as (a − b)(a2 + ab + b2).
Try it!
Factor: x3 + 64.
Solution





Try it! – Factoring a Difference of Cubes
Factor: 8x3 − 125.
Solution
Notice that 8x3 and 125 are cubes because 8x3 = (2x)3 and 125 = 53. Write the difference of cubes as (2x − 5)(4x2 + 10x + 25).
Analysis
Just as with the sum of cubes, we will not be able to further factor the trinomial portion.
General Strategy to Factor Polynomials
You have now become acquainted with all the methods of factoring that you will need in this course. The following chart summarizes all the factoring methods we have covered, and outlines a strategy you should use when factoring polynomials.

Use a general strategy for factoring polynomials.
- Is there a greatest common factor?
Factor it out. - Is the polynomial a binomial, trinomial, or are there more than three terms?
If it is a binomial:- Is it a sum?
Of squares? Sums of squares do not factor.
Of cubes? Use the sum of cubes pattern. - Is it a difference?
Of squares? Factor as the Difference of Squares.
Of cubes? Use the difference of cubes pattern.
- Is it of the form
x2 + bx + c? Undo FOIL. - Is it of the form
ax2 + bx + c?
If a and c are squares, check if it fits the trinomial square pattern.
Use the trial and error or “ac” method.
If it has more than three terms:
- Use the grouping method.
- Is it a sum?
- Check.
Is it factored completely?
Do the factors multiply back to the original polynomial?
Remember, a polynomial is completely factored if, other than monomials, its factors are prime!
Try it
Factor completely: 7x3 − 21x2 − 70x.
Solution
| Steps | Algebraic |
| Example | 7x3 − 21x2 − 70x |
| Is there a GCF? Yes, 7x. Factor out the GCF. | 7x(x2 − 3x − 10) |
| In the parentheses, is it a binomial, trinomial, or are there more terms? | Trinomial with leading coefficient 1. |
| “Undo” FOIL. | 7x(x )(x ) = 7x(x + 2)(x − 5) |
| Is the expression factored completely? | Yes. Neither binomial can be factored. |
| Check by multiplying: | 7x(x + 2)(x − 5)
7x(x2 − 5x + 2x − 10) 7x(x2 − 3x − 10) 7x3 − 21x2 − 70x ✓ |
Try it!
Factor completely: 24y2 − 150.
Solution
| Steps | Algebraic |
| Example | 24y2 − 150 |
| Is there a GCF? Yes, 6—factor it out! | 6(4y2 − 25) |
| In the parentheses, is it a binomial, trinomial or are there more than three terms? | Binomial. |
| Is it a sum? | No. |
| Is it a difference? Of squares or cubes? Yes, squares. | 6((2y)2 − (5)2) |
| Write as a product of conjugates. | 6(2y − 5)(2y + 5) |
| Is the expression factored completely? | Neither binomial can be factored. |
| Check by multiplying: | 6(2y − 5)(2y + 5)
6(4y2 − 25) 24y2 − 150 ✓ |
The next example can be factored using several methods. Recognizing the trinomial squares pattern will make your work easier.
Try it!
Factor completely: 4a2 − 12ab + 9b2.
Solution
| Steps | Algebraic |
| Example | 4a2 − 12ab + 9b2 |
| Is there a GCF? | No. |
| Is it a binomial, trinomial, or are there more terms? | Trinomial with a≠1. But the first term is a perfect square. |
| Is the last term a perfect square? Yes. | (2a)2 − 12ab + (3b)2 |
| Does it fit the pattern,a2−2ab+b2? Yes. Write it as a square. | (2a)2 ↘ − 12ab + − 2(2a)(3b) ↙ (3b)2 |
| Is the expression factored completely? | Yes. |
| Check by multiplying: | (2a − 3b)2
(2a)2 − 2 · 2a · 3b + (3b)2 4a2 − 12ab + 9b2 ✓ |
When we have factored a polynomial with four terms, most often we separated it into two groups of two terms. Remember that we can also separate it into a trinomial and then one term.
Try it!
Factor completely: 9x2 − 12xy + 4y2 − 49.
Solution
| Steps | Algebraic |
| Example | 9x2 − 12xy + 4y2 − 49 |
| Is there a GCF? . | No |
| With more than 3 terms, use grouping. Last 2 terms have no GCF. Try grouping first 3 terms. | 9x2 − 12xy + 4y2 − 49 |
| Factor the trinomial with a ≠ 1. But the first term is a perfect square. | |
| Is the last term of the trinomial a perfect square? Yes. | (3x)2−12xy+(2y)2−49 |
| Does the trinomial fit the pattern, a2 − 2ab + b2?Yes. | (3x)2 ↘ −12xy + −2(3x)(2y) ↙ (2y)2 − 49 |
| Write the trinomial as a square. | (3x − 2y)2 − 49 |
| Is this binomial a sum or difference? Of squares or cubes? Write it as a difference of squares. | (3x − 2y)2 − 72 |
| Write it as a product of conjugates. | ((3x − 2y) −7)((3x − 2y) +7)(3x − 2y − 7)(3x − 2y + 7) |
| Is the expression factored completely? | Yes. |
| Check by multiplying: | (3x − 2y + 7)
9x2 − 6xy − 21x − 6xy + 4y2 + 14y + 21x − 14y − 49 9x2 − 12xy + 4y2 − 49✓ |
Factoring Expressions with Fractional or Negative Exponents
Expressions with fractional or negative exponents can be factored by pulling out a GCF. Look for the variable or exponent that is common to each term of the expression and pull out that variable or exponent raised to the lowest power. These expressions follow the same factoring rules as those with integer exponents. For instance, 2x1/4 + 5x3/4 can be factored by pulling out x1/4 and being rewritten as x1/4(2 + 5x1/2).
Try it! – Factoring an Expression with Fractional or Negative Exponent Factor
Factor: 3x(x + 2)−1/3 + 4(x +2)2/3.
Solution
Factor out the term with the lowest value of the exponent. In this case, that would be (x + 2)−1/3.
Access these online resources for additional instruction and practice with factoring polynomials.
Key Concepts
| Steps | Algebraic |
| difference of squares | a2 − b2=(a + b)(a − b) |
| perfect square trinomial | a2 + 2ab + b2=(a + b)2 |
| sum of cubes | a3 + b3=(a + b)(a2 − ab + b2) |
| difference of cubes | a3 − b3=(a − b)(a2 + ab + b2) |
- Write the factors as two binomials with first terms x.
- Find two numbers m and n that
- multiply to c, m · n = c
- add to b, m + n = b
- Use m and n as the last terms of the factors.
(x + m)(x + n) - Check by multiplying the factors.
- The greatest common factor, or GCF, can be factored out of a polynomial. Checking for a GCF should be the first step in any factoring problem.
- Trinomials with leading coefficient 1 can be factored by finding numbers that have a product of the third term and a sum of the second term.
- Trinomials can be factored using a process called factoring by grouping.
- Perfect square trinomials and the difference of squares are special products and can be factored using equations.
- The sum of cubes and the difference of cubes can be factored using equations.
- Polynomials containing fractional and negative exponents can be factored by pulling out a GCF.

