2 Expressions, Properties of Real Numbers
Topics Covered:
- Simplify Expressions with Absolute Value
- Simplify Expressions and Order of Operations
- Identify and Combine Like Terms
- Evaluate Variable Expressions with Integers
- Properties of Real Numbers
- Using Commutative and Associative Properties
- Identity, Inverse, and Zero Properties
- Distributive Property
- Key Concepts
Simplify Expressions with Absolute Value
A negative number is a number less than 0. The negative numbers are to the left of zero on the number line.
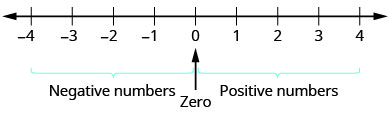
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers 2 and -2 are the same distance from zero, each one is called the opposite of the other. The opposite of 2 is −2, and the opposite of −2 is 2.
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.

−a means the opposite of the number a.
The notation −a is read as “the opposite of a.”
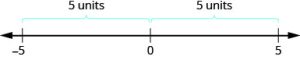
We saw that numbers such as 3 and −3 are opposites because they are the same distance from 0 on the number line. They are both three units from 0. The distance between 0 and any number on the number line is called the absolute value of that number.
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as |n| and |n| ≥ 0 for all numbers.
Absolute values are always greater than or equal to zero.
For example,
−5 is 5 units away from 0, so |-5| = 5.
5 is 5 units away from 0, so |5| = 5.
The image below illustrates this idea.
The absolute value of a number is never negative because distance cannot be negative. The only number with absolute value equal to zero is the number zero itself because the distance from 0 to 0 on the number line is zero units.
In the next example, we’ll order expressions with absolute values.
Try it!
Fill in <, >, or = for each of the following pairs of numbers:
a. ![]() b.
b. ![]() c.
c. ![]() d.
d. ![]() .
.
Solution:
a.
| Steps | Algebraic |
| Example | |
| Simplify | |
| Order | |
| Solution |
b.
| Steps | Algebraic |
| Example | |
| Simplify | |
| Order | |
| Solution |
c.
| Steps | Algebraic |
| Simplify | |
| Order | |
d.
| Steps | Algebraic |
| Example | |
| Simplify | |
| Order | |
| Solution |
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number.
| Common Grouping Symbols | |
|---|---|
| parentheses | ( ) |
| brackets | [ ] |
| braces | { } |
| Absolute value | | | |
In the next example, we simplify the expressions inside absolute value bars first just like we do with parentheses.
Try it!
Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Example | 24 − |19 − 3(6 − 2)| |
| Work inside parentheses first: | |
| subtract 2 from 6 | 24 − |19 − 3(4)| |
| Multiply 3(4) | 24 − |19 − 12| |
| Subtract inside the absolute value bars. | 24 − |7| |
| Take the absolute value. | 24 − 7 |
| Subtract. | 17 |
Simplify Expressions and Order of Operations
What is the difference in English between a phrase and a sentence? A phrase expresses a single thought that is incomplete by itself, but a sentence makes a complete statement. A sentence has a subject and a verb. In algebra, we have expressions and equations.
An expression is a number, a variable, or a combination of numbers and variables using operation symbols.
| Expression | Words | English Phrase |
|---|---|---|
| 3 + 5 | 3 plus 5 | the sum of three and five |
| n − 1 | n minus one | the difference of n and one |
| 6 · 7 | 6times7 | the product of six and seven |
| x divided by y | the quotient of x and y |
An equation is two expressions linked by an equal sign. When you read the words the symbols represent in an equation, you have a complete sentence in English. The equal sign gives the verb.
| Equation | English Phrase |
|---|---|
| 3 + 5 = 8 | the sum of three and five is equal to eight. |
| n − 1 = 14 | the difference of n and one equals fourteen. |
| 6 · 7 = 42 | the product of six and seven is equal to forty-two. |
| x = 53 |
x is equal to fifty-three. |
| y + 9 = 2y − 3 | y plus nine is equal to two y minus three. |
To simplify an expression means to do all the math possible. For example, to simplify 4 · 2 + 1 we would first multiply 4 · 2 to get 8 and then add the 1 to get 9. A good habit to develop is to work down the page, writing each step of the process below the previous step. The example just described would look like this:
| Steps |
| 4 · 2 + 1 |
| 8 + 1 |
| 9 |
By not using an equal sign when you simplify an expression, you may avoid confusing expressions with equations.
To simplify an expression, do all operations in the expression.
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values.
For example, consider the expression 4 + 3 · 7. Some students simplify this getting 49, by adding 4 + 3 and then multiplying that result by 7. Others get 25, by multiplying 3 · 7 first and then adding 4.
The same expression should give the same result. So mathematicians established some guidelines that are called the order of operations.
How to use the order of operations.
-
- Parentheses and Other Grouping Symbols
-
- Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
-
- Exponents
-
- Simplify all expressions with exponents.
-
- Multiplication and Division
-
- Perform all multiplication and division in order from left to right. These operations have equal priority.
-
- Addition and Subtraction
-
- Perform all addition and subtraction in order from left to right. These operations have equal priority.
-
- Parentheses and Other Grouping Symbols
Students often ask, “How will I remember the order?” Here is a way to help you remember: Take the first letter of each key word and substitute the silly phrase “Please Excuse My Dear Aunt Sally”.
| Order of Operations | |
|---|---|
| Please | Parentheses |
| Excuse | Exponents |
| My Dear | Multiplication and Division |
| Aunt Sally | Addition and Subtraction |
It’s good that “My Dear” goes together, as this reminds us that multiplication and division have equal priority. We do not always do multiplication before division or always do division before multiplication. We do them in order from left to right.
Similarly, “Aunt Sally” goes together and so reminds us that addition and subtraction also have equal priority and we do them in order from left to right.
Try it!
Simplify: 18 ÷ 6 + 4(5 − 2).
Solution:
| Steps | Algebraic |
| Parentheses? Yes, subtract first. | 18 ÷ 6 + 4(5 − 2). |
| Exponents? No. | 18 ÷ 6 + 4(3) |
| Multiplication or division? | Yes. |
| Divide first because we multiply and divide left to right. | 3 + 4(3) |
| Any other multiplication or division? | Yes. |
| Multiply. | 3 + 12 |
| Any other multiplication of division? | No. |
| Any addition or subtraction? | Yes. |
| Add. | 15 |
Try it!
- Simplify: 5 + 23 + 3[6 − 3(4 − 2)].
Solution:
| Steps | Algebraic |
| Example | 5 + 23 + 3[6 − 3(4 − 2)] |
| Are there any parentheses (or other grouping symbols)? Yes. |
5 + 23 + 3[6 − 3(4 − 2)] |
| Focus on the parentheses that are inside the brackets. Subtract. |
5 + 23 + 3[6 − 3(2)] |
| Continue inside the brackets and multiply. | 5 + 23 + 3[6 − 6] |
| Continue inside the brackets and subtract. | 5 + 23 + 3[0] |
| The expression inside the brackets requires no further simplification. |
|
| Are there any exponents? Yes. Simplify exponents. | 5 + 8 + 3[0] |
| Is there any multiplication or division? Yes. | Yes. |
| Multiply. | 5 + 8 + 0 |
| Is there any addition of subtraction? | Yes. |
| Add. | 13 + 0 |
| Add. | 13 |
2. Simplify: 9 + 53 − [4(9 + 3)].
Solution:
86
3. Simplify: a. (−2)4 b. -24
Solution:
Notice the difference in parts (a) and (b). In part (a), the exponent means to raise what is in the parentheses, the −2 to the 4th power. In part (b), the exponent means to raise just the 2 to the 4th power and then take the opposite.
a.
| Steps | Algebraic |
| Example | (−2)4 |
| Write in expanded form | (−2)(−2)(−2)(−2) |
| Multiply | 4(−2)(−2) |
| Multiply | −8(−2) |
| Multiply | 16 |
b.
| Steps | Algebraic |
| Example | -24 |
| Write in expanded form. | −(2 · 2 · 2 · 2) |
| We are asked to find the opposite of 24. | |
| Multiply. | −(4 · 2 · 2) |
| Multiply. | −(8 · 2) |
| Multiply. | -16 |
The last example showed us the difference between (−2)4 and −24. This distinction is important to prevent future errors. The next example reminds us to multiply and divide in order left to right.
Try it!
Simplify: a. 8(−9) ÷ (−2)3. b. −30 ÷ 2 + (−3)(−7).
Solution:
a.
| Steps | Algebraic |
| Example | 8(−9) ÷ (−2)3 |
| Exponents first. | 8(−9) ÷ (−8) |
| Multiply. | -72 ÷ (−8) |
| Divide. | 9 |
b.
| Steps | Algebraic |
| Example | −30 ÷ 2 + (−3)(−7) |
| Multiply and divide left to right, so divide first | −15 + (−3)(−7) |
| Multiply. | −15 + 21 |
| Add. | 6 |
Identify and Combine Like Terms
Algebraic expressions are made up of terms. What do you think 3x + 6x would simplify to? If you thought 9x, you would be right!
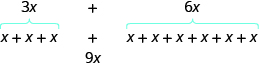
We can see why this works by writing both terms as addition problems. Add the coefficients and keep the same variable. It doesn’t matter what x is. If you have 3 of something and add 6 more of the same thing, the result is 9 of them. For example, 3 oranges plus 6 oranges is 9 oranges. We will discuss the mathematical properties behind this later.
A term is a constant or the product of a constant and one or more variables.
Examples of terms are 7, y, 5x2, 9a, and b5.
The coefficient of a term is the constant that multiplies the variable in a term.
Think of the coefficient as the number in front of the variable. The coefficient of the term 3x is 3. When we write x, the coefficient is 1, since x = 1 · x.
Some terms share common traits. When two terms are constants or have the same variable and exponent, we say they are like terms.
Look at the following 6 terms. Which ones seem to have traits in common?
We say,
![]() 7 and 4 are like terms.
7 and 4 are like terms.
![]() 5x and 3x are like terms.
5x and 3x are like terms.
![]() n2 and 9n2 are like terms.
n2 and 9n2 are like terms.
Terms that are either constants or have the same variables raised to the same powers are called like terms.
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add or subtract the coefficients and keep the same variable for each group of like terms.
If there are like terms in an expression, you can simplify the expression by combining the like terms. We add the coefficients and keep the same variable.
| Steps | Algebraic |
| Simplify | 4x + 7x + x |
| Add the coefficients | 12x |
Try it!
Solution:



2. Simplify: 3x2 + 7x + 9 + 7x2 + 9x + 8.
Solution:
10x2 + 16x + 17
Evaluate Variable Expressions with Integers
In the last few examples, we simplified expressions using the order of operations. Now we’ll evaluate some expressions—again following the order of operations. To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression, substitute that number for the variable in the expression and then simplify the expression.
Try it!
- Evaluate when x = 4: a. x2 b. 3x c. 2x2 + 3x + 8.
Solution:
a.
| Steps | Algebraic |
| Example | x2 |
| Replace x with 4 | 42 |
| Use definition of exponent. | 4 · 4 |
| Simplify. | 16 |
b.
| Steps | Algebraic |
| 3x | |
| Replace x with 4 | 34 |
| Use definition of exponent. | 3 · 3 · 3 · 3 |
| Simplify. | 81 |
c.
| Steps | Algebraic |
| Example | 2x2 + 3x + 8 |
| Replace x with 4 | 2(4)2 + 3(4) + 8 |
| Follow the order of operations | 2(16) + 3(4) + 8 |
| Simplify. | 32 + 12 + 8 |
| 52 |
2. Evaluate when x = 3, a. x2 b. 4x c. 3x2 + 4x + 1.
Solution:
a. 9 b. 64 c. 40
Remember that to evaluate an expression means to substitute a number for the variable in the expression. Now we can use negative numbers as well as positive numbers.
Try it!
Evaluate 4x2 − 2xy + 3y2 when x = 2, y = −1.
Solution:
| Steps | Algebraic |
| Example | 4x2 − 2xy + 3y2 |
| Substitute x = 2, y = -1. Use parentheses to show multiplication | 4(2)2 − 2(2)(-1) + 3(-1)2 |
| Simplify exponents. | 4 · 4 – (-4) + 3 · 1 |
| Multiply. | 16 – (-4) + 3 |
| Subtract. | 20 + 3 |
| Add. | 23 |
Properties of Real Numbers
We have already described numbers as counting numbers, whole numbers, and integers. What is the difference between these types of numbers? Difference could be confused with subtraction. How about asking how we distinguish between these types of numbers?
| Steps | Algebraic |
| Counting numbers | 1, 2, 3, 4, ….. |
| Whole numbers | 0, 1, 2, 3, 4, …. |
| Integers | …., −3, −2, −1, 0, 1, 2, 3, …. |
What type of numbers would we get if we started with all the integers and then included all the fractions? The numbers we would have form the set of rational numbers. A rational number is a number that can be written as a ratio of two integers.
In general, any decimal that ends after a number of digits (such as 7.3 or −1.2684) is a rational number. We can use the place value of the last digit as the denominator when writing the decimal as a fraction. The decimal for ![]() is the number
is the number ![]() . The bar over the 3 indicates that the number 3 repeats infinitely. Continuously has an important meaning in calculus. The number(s) under the bar is called the repeating block and it repeats continuously.
. The bar over the 3 indicates that the number 3 repeats infinitely. Continuously has an important meaning in calculus. The number(s) under the bar is called the repeating block and it repeats continuously.
Since all integers can be written as a fraction whose denominator is 1, the integers (and so also the counting and whole numbers) are rational numbers.
A rational number is a number that can be written both as a ratio of integers ![]() where p and q are integers and q ≠ 0, and as a decimal that stops or repeats.
where p and q are integers and q ≠ 0, and as a decimal that stops or repeats.
Its decimal form stops or repeats.
Are there any decimals that do not stop or repeat? Yes! The number π (the Greek letter pi, pronounced “pie”), which is very important in describing circles, has a decimal form that does not stop or repeat. We use three dots (…) to indicate the decimal does not stop or repeat.
The square root of a number that is not a perfect square is a decimal that does not stop or repeat.
An irrational number is a number that cannot be written as the ratio of two integers. i.e. A number whose decimal form does not stop or repeat cannot be written as a fraction of integers. We call this an irrational number.
Let’s summarize a method we can use to determine whether a number is rational or irrational.
If the decimal form of a number
- repeats or stops, the number is a rational number.
- does not repeat and does not stop, the number is an irrational number.
We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers. The irrational numbers are numbers whose decimal form does not stop and does not repeat. When we put together the rational numbers and the irrational numbers, we get the set of real numbers.
A real number is a number that is either rational or irrational.
Later in this course we will introduce numbers beyond the real numbers. The image below illustrates how the number sets we’ve used so far fit together.
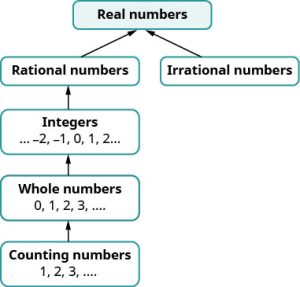
Does the term “real numbers” seem strange to you? Are there any numbers that are not “real,” and, if so, what could they be? Can we simplify ![]() ? Is there a number whose square is −25?
? Is there a number whose square is −25?
None of the numbers that we have dealt with so far has a square that is −25. Why? Any positive number squared is positive. Any negative number squared is positive. So we say there is no real number equal to ![]() . The square root of a negative number is not a real number.
. The square root of a negative number is not a real number.
Try it!
Given the numbers ![]() , list the a. whole numbers b. integers c. rational numbers d. irrational numbers e. real numbers.
, list the a. whole numbers b. integers c. rational numbers d. irrational numbers e. real numbers.
Solution:
a. Remember, whole numbers are 0, 1, 2, 3, …, so 8 is the only whole number given.
b. Integers are whole numbers and their opposites (which includes 0). So the whole number 8 is an integer, and −7 is the opposite of a whole number so it is an integer, too. Also, notice that 64 is the square of 8 so –![]() -8. So the integers are −7, 8, and –
-8. So the integers are −7, 8, and –![]() .
.
c. Since all integers are rational, then −7, 8, and –![]() are rational. Rational numbers also include fractions and decimals that repeat or stop, so
are rational. Rational numbers also include fractions and decimals that repeat or stop, so ![]() and 5.9 are rational. So the list of rational numbers is –
and 5.9 are rational. So the list of rational numbers is –![]() , and –
, and –![]() .
.
d. Remember that 5 is not a perfect square, so ![]() is irrational.
is irrational.
e. All the numbers listed are real numbers.
Using Commutatitve and Associative Properties
The order we add two numbers doesn’t affect the result. If we add 8 + 9 or 9 + 8, the results are the same—they both equal 17. So, 8 + 9 = 9 + 8. The order in which we add does not matter!
Similarly, when multiplying two numbers, the order does not affect the result. If we multiply 9 · 8 or 8 · 9 the results are the same—they both equal 72. So, 9 · 8 = 8 · 9. The order in which we multiply does not matter!
These examples illustrate the Commutative Property.
| of Addition | If a and b are real numbers, then a + b = b + a. |
| of Multiplication | If a and b are real numbers, then a · b = b · a. |
The Commutative Property has to do with order. We subtract 9 − 8 and 8 − 9, and see that 9 − 8 ≠ 8 − 9. Since changing the order of the subtraction does not give the same result, we know that subtraction is not commutative.
Division is not commutative either. Since 12 ÷ 3 ≠ 3 ÷ 12, changing the order of the division did not give the same result. The commutative properties apply only to addition and multiplication! Subtraction and division are not commutative.
When adding three numbers, changing the grouping of the numbers gives the same result. For example, (7 + 8) + 2 = 7 + (8 + 2), since each side of the equation equals 17.
This is true for multiplication, too. For example, ![]() , since each side of the equation equals 5.
, since each side of the equation equals 5.
These examples illustrate the Associative Property.
| of Addition | If a, b, and c are real numbers,
then (a + b) + c = a + (b + c). |
| of Multiplication | If a, b, and c are real numbers,
then (a · b) · c = a · (b · c). |
The Associative Property has to do with grouping. If we change how the numbers are grouped, the result will be the same. Notice it is the same three numbers in the same order—the only difference is the grouping.
We saw that subtraction and division were not commutative. They are not associative either.
| Ex. 1 | Ex. 2 |
| (10 − 3) − 2 ≠ 10 − (3 − 2) | (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2) |
| 7 − 2 ≠ 10 − 1 | 6 ÷ 2 ≠ 24 ÷ 2 |
| 5 ≠ 9 | 3 ≠ 12 |
When simplifying an expression, it is always a good idea to plan what the steps will be. In order to combine like terms in the next example, we will use the Commutative Property of addition to write the like terms together.
Try it!
- Simplify: 18p + 6q + 15p + 5q.
Solution:
| Steps | Algebraic |
| Example | 18p + 6q + 15p + 5q |
| Use the Commutative Property of addition to reorder so that like terms are together. | 18p + 15p + 6q + 5q |
| Add like terms. | 33p + 11q |
2. Simplify: 23r + 14s + 9r + 15s.
Solution:
32r + 29s
When we have to simplify algebraic expressions, we can often make the work easier by applying the Commutative Property or Associative Property first.
Try it!
Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Example | |
| Notice that the last 2 terms have a common denominator, so change the grouping. | |
| Add in parentheses first. | |
| Simplify the fraction. | |
| Add. | |
| Convert to an improper fraction. |
Identity, Inverse, and Zero Properties
What happens when we add 0 to any number? Adding 0 doesn’t change the value. For this reason, we call 0 the additive identity. The Identity Property of Addition states that for any real number a, a + 0 = a and 0 + a = a.
What happens when we multiply any number by one? Multiplying by 1 doesn’t change the value. So we call 1 the multiplicative identity. The Identity Property of Multiplication states that for any real number a, a · 1 = a and 1 · a = a.
Identity Property
| of Addition
0 is the additive identity |
For any real number a: a + 0 = a 0 + a = a |
| of Multiplication
1 is the multiplicative identity |
For any real number a: a · 1 = a 1 · a = a |
We call −a the additive inverse of a. The opposite of a number is its additive inverse. A number and its opposite add to zero, which is the additive identity. This leads to the Inverse Property of Addition that states for any real number a, a + (−a) = 0.
What number multiplied by ![]() gives the multiplicative identity, 1? In other words,
gives the multiplicative identity, 1? In other words, ![]() times what results in 1? We know
times what results in 1? We know
![]()
We call ![]() the multiplicative inverse of a. The reciprocal of a number is its multiplicative inverse. This leads to the Inverse Property of Multiplication that states that for any real number
the multiplicative inverse of a. The reciprocal of a number is its multiplicative inverse. This leads to the Inverse Property of Multiplication that states that for any real number ![]() .
.
Inverse Property
| of Addition | For any real number a, a + (−a) = 0 −a is the additive inverse of a A number and its opposite add to zero. |
| of Multiplication | For any real number A number and its reciprocal multiply to one. |
The Identity Property of addition says that when we add 0 to any number, the result is that same number. What happens when we multiply a number by 0? Multiplying by 0 makes the product equal zero.
What about division involving zero? What is 0 ÷ 3? Think about a real example: If there are no cookies in the cookie jar and 3 people are to share them, how many cookies does each person get? There are no cookies to share, so each person gets 0 cookies. So, 0 ÷ 3 = 0.
We can check division with the related multiplication fact. So we know 0 ÷ 3 = 0 because 0 · 3 = 0.
Now think about dividing by zero. What is the result of dividing 4 by 0? Think about the related multiplication fact:
4 ÷ 0 = ? means ? · 0 = 4
Is there a number that multiplied by 0 gives 4? Since any real number multiplied by 0 gives 0, there is no real number that can be multiplied by 0 to obtain 4. We conclude that there is no answer to 4 ÷ 0 and so we say that division by 0 is undefined.
Multiplication by Zero: For any real number a,
| a · 0 = 0 0 · a = 0 | The product of any number and 0 is 0. |
Division by Zero: For any real number a, a ≠ 0
| Zero divided by any real number, except itself, is zero. | |
| Division by zero is undefined. |
Try it!
1. Simplify: −84n + (−73n) + 84n
Solution:
| Steps | Algebraic |
| Example | −84n + (−73n) + 84n |
| Notice that the first and third terms are opposites; use the Commutative Property of addition to re-order the terms. | −84n + 84n + (−73n) |
| Add left to right. | 0 + (−73n) |
| Add. | −73n |
Solution:
−48a
Now we will see how recognizing reciprocals is helpful. Before multiplying left to right, look for reciprocals—their product is 1.
Try it!
Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Example | |
| Notice the first and third terms are reciprocals, so use the Commutative Property of multiplication to re-order the factors. | |
| Multiply left to right. | |
| Multiply. |
The next example makes us aware of the distinction between dividing 0 by some number or some number being divided by 0.
Try it!
1. Simplify: a. ![]() . b.
. b. ![]()
![]() .
.
Solution:
a.
| Steps | Algebraic |
| Example | |
| Zero divided by any real number except itself is 0 | 0 |
b.
| Steps | Algebraic |
| Example | |
| Division by 0 is undefined | undefined |
2. Simplify: a. ![]() . b.
. b. ![]()
![]() .
.
Solution:
a. 0 b. undefined
Distributive Property
Suppose that three friends are going to the movies. They each need $9.25—that’s 9 dollars and 1 quarter—to pay for their tickets. How much money do they need all together?
You can think about the dollars separately from the quarters. They need 3 times $9 so $27 and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.
If a, b, and c are real numbers, then
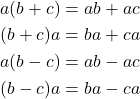
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions.
Try it!
1. Simplify: 3(x + 4).
Solution:
| Steps | Algebraic |
| Example | 3(x + 4) |
| Distribute. | 3 · x + 3 · 4 |
| Multiply. | 3x + 12 |
2. Simplify: 4(x + 2).
Solution:
4x + 8
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in the first example above would look like this:
![]()
Try it!
Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Example | 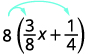 |
| Distribute | |
| Multiply |
Using the Distributive Property as shown in the next example will be very useful when we solve money applications in later chapters.
Try it!
Simplify: 100(0.3 + 0.25q).
Solution:
| Steps | Algebraic |
| Example | |
| Distribute. | |
| Multiply. |
When we distribute a negative number, we need to be extra careful to get the signs correct!
Try it!
Simplify: −11(4 − 3a).
Solution:
| Steps | Algebraic |
| Example | −11(4 − 3a) |
| Distribute. | −11 · 4 − (−11) · 3a |
| Multiply. | −44 − (−33a) |
| Simplify. | −44 + 33a |
Notice that you could also write the result as 33a − 44. Do you know why?
In the next example, we will show how to use the Distributive Property to find the opposite of an expression.
Try it!
1. Simplify: −(y + 5).
Solution:
| Steps | Algebraic |
| −(y + 5) | |
| Multiplying by −1 results in the opposite | −1(y + 5) |
| Distribute. | −1 · y + (−1) · 5 |
| Simplify. | −y + (−5) |
| Simplify. | −y − 5 |
2. Simplify: −(x − 4).
Solution:
−x + 4
There will be times when we’ll need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be to multiply using the Distributive Property, which removes the parentheses. The next two examples will illustrate this.
Try it!
1. Simplify: 8 − 2(x + 3)
Solution:
We follow the order of operations. Multiplication comes before subtraction, so we will distribute the 2 first and then subtract.
| Steps | Algebraic |
| Example | 8 − 2(x + 3) |
| Distribute. | 8 − 2 · x − 2 · 3 |
| Multiply. | 8 − 2x − 6 |
| Combine like terms. | −2x + 2 |
2. Simplify: 4(x − 8) − (x + 3).
Solution:
| Steps | Algebraic |
| Example | 4(x − 8) − (x + 3) |
| Distribute. | 4x − 32 − x − 3 |
| Combine like terms. | 3x − 35 |
All the properties of real numbers we have used in this chapter are summarized here.
| Property |
Algebraic |
| Commutative Property | |
| When adding or multiplying, changing the order gives the same result | |
| of addition If a, b are real numbers, then | a + b = b + a |
| of multiplication If a, b are real numbers, then | a · b = b · a |
| Associative Property | |
| When adding or multiplying, changing the grouping gives the same result. | |
| of addition: If a, b, and c are real numbers, then | (a + b) + c = a + (b + c) |
| of multiplication: If a, b, and c are real numbers, then | (a · b) · c = a · (b · c) |
| Distributive Property | |
| If a, b, and c are real numbers, then | a(b + c) = ab + ac |
| (b + c)a = ba + ca | |
| a(b − c) = ab − ac | |
| (b − c)a = ba − ca | |
| Identity Property | |
| of addition: For any real number a | a + 0 = a |
| 0 is the additive identity | 0 + a = a |
| of multiplication: For any real number a | a · 1 = a |
| 1 is the multiplicative identity | 1 · a = a |
| Inverse Property |
|
| of addition: For any real number a, | a + (−a) = 0 |
| −a is the additive inverse of a | A number and its opposite add to zero. |
| of multiplication: For any real number a, a ≠ 0 | |
| |
A number and its reciprocal multiply to one. |
| Properties of Zero | |
| For any real number a, | a · 0 = 0 |
| 0 · a = 0 | |
| For any real number a, a ≠ 0 | |
| For any real number a, | |
Key Concepts
- Opposite Notation
−a means the opposite of the number a
The notation −a is read as “the opposite of a.” - Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as |n| and |n| ≥ 0 for all numbers.
Absolute values are always greater than or equal to zero
- Grouping Symbols
Parentheses ( ) Braces { }
Brackets [ ] Absolute value | | - Subtraction Property
a − b = a + (−b)
Subtracting a number is the same as adding its opposite. - Multiplication and Division of Signed Numbers
For multiplication and division of two signed numbers:
| Same signs | Result |
|---|---|
| • Two positives | Positive |
| • Two negatives | Positive |
If the signs are the same, the result is positive.
| Different signs | Result |
|---|---|
| • Positive and negative | Negative |
| • Negative and positive | Negative |
If the signs are different, the result is negative.
- Multiplication by -1
−1a = −a
Multiplying a number by −1 gives its opposite. - How to Use Integers in Applications.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
| Property |
Algebraic |
| Commutative Property | |
| When adding or multiplying, changing the order gives the same result | |
| of addition If a, b are real numbers, then | a + b = b + a |
| of multiplication If a, b are real numbers, then | a · b = b · a |
| Associative Property | |
| When adding or multiplying, changing the grouping gives the same result. | |
| of addition: If a, b, and c are real numbers, then | (a + b) + c = a + (b + c) |
| of multiplication: If a, b, and c are real numbers, then | (a · b) · c = a · (b · c) |
| Distributive Property | |
| If a, b, and c are real numbers, then | a(b + c) = ab + ac |
| (b + c)a = ba + ca | |
| a(b − c) = ab − ac | |
| (b − c)a = ba − ca | |
| Identity Property | |
| of addition: For any real number a | a + 0 = a |
| 0 is the additive identity | 0 + a = a |
| of multiplication: For any real number a | a · 1 = a |
| 1 is the multiplicative identity | 1 · a = a |
| Inverse Property |
|
| of addition: For any real number a, | a + (−a) = 0 |
| −a is the additive inverse of a | A number and its opposite add to zero. |
| of multiplication: For any real number a, a ≠ 0 | |
| |
A number and its reciprocal multiply to one. |
| Properties of Zero | |
| For any real number a, | a · 0 = 0 |
| 0 · a = 0 | |
| For any real number a, a ≠ 0 | |
| For any real number a, | |

