2 Expressions, Properties of Real Numbers
Topics Covered:[1]
- Simplify Expressions with Absolute Value
- Simplify Expressions and Order of Operations
- Identify and Combine Like Terms
- Evaluate Variable Expressions with Integers
- Properties of Real Numbers
- Using Commutative and Associative Properties
- Identity, Inverse, and Zero Properties
- Distributive Property
- Key Concepts
Simplify Expressions with Absolute Value
A negative number is a number less than 0. The negative numbers are to the left of zero on the number line.
![\[\LARGE{ \begin{center} \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{-4 \quad -3 \quad -2 \quad -1\quad 0 \quad 1 \quad 2 \quad 3 \quad 4} \\ \;{\color{mypurple1}\underbrace{\quad{\quad\quad\quad\quad\quad\quad\quad\quad }}_{\boldsymbol{\textcolor{black}{{Negative Numbers}}}}\textbf{Zero}{\color{mypurple1}\underbrace{\quad{\quad\quad \quad\quad\quad\quad\quad }}_{\boldsymbol{\textcolor{black}{{Positive Numbers}}}}\\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4a9d1a575d1bb9be1740cbc9e793ff43_l3.png "Rendered by QuickLaTeX.com")
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers 2 and -2 are the same distance from zero, each one is called the opposite of the other. The opposite of 2 is −2, and the opposite of −2 is 2.
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
![\[\LARGE{ \begin{center} \;{\color{mypurple1}\overbrace{\quad\quad\quad\quad\quad\quad\quad }}^{3}\:\color{mypurple1}\overbrace{\; \quad \quad\quad\quad\quad\quad }}^{3}\\ \overleftrightarrow{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{-4 \quad {\color{mypurple1}-3} \quad -2 \quad -1\quad {0 \quad 1 \quad 2 \quad {\color{mypurple1}3} \quad 4} \\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5707851d7c2413b4e3e9422202ec70fd_l3.png "Rendered by QuickLaTeX.com")
−a means the opposite of the number a.
The notation −a is read as “the opposite of a.”
We saw that numbers such as 3 and −3 are opposites because they are the same distance from 0 on the number line. They are both three units from 0. The distance between 0 and any number on the number line is called the absolute value of that number.
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as |n| and |n| ≥ 0 for all numbers.
Absolute values are always greater than or equal to zero.
For example,
−5 is 5 units away from 0, so |-5| = 5.
5 is 5 units away from 0, so |5| = 5.
The image below illustrates this idea.
![\[\LARGE{ \begin{center} \;{\color{mypurple1}\overbrace{\;\quad\quad\quad\quad }}^{\textbf{5 units}}\:\color{mypurple1}\overbrace{\; \quad \quad\quad\quad }}^{\textbf{5 units}}\\ \overleftrightarrow{\quad\quad\;\quad\quad\quad\quad\quad\quad\quad\quad\quad} \\ \textbf{{\color{mypurple1}-5} \quad \quad \quad 0 \quad \quad \quad {\color{mypurple1}5} \quad } \\ \end{center} }\]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3132bf89903b24331b9403b2069c6899_l3.png "Rendered by QuickLaTeX.com")
The absolute value of a number is never negative because distance cannot be negative. The only number with absolute value equal to zero is the number zero itself because the distance from 0 to 0 on the number line is zero units.
In the next example, we’ll order expressions with absolute values.
Try it!
Fill in <, >, or = for each of the following pairs of numbers:
a. 
b. 
c. 
d. 
.
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Example | |
| Simplify |  |
| Order |  |
| Solution |  |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Example | |
| Simplify |  |
| Order |  |
| Solution |  |
Solution C (click to reveal)
c.
| Steps | Algebraic |
| Example | |
| Simplify |  |
| Order |  |
| Solution |  |
Solution D (click to reveal)
d.
| Steps | Algebraic |
| Example | |
| Simplify |  |
| Order |  |
| Solution |  |
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number. See the table below for a summary.
| Common Grouping Symbols | |
|---|---|
| parentheses | ( ) |
| brackets | [ ] |
| braces | { } |
| Absolute value | | | |
In the next example, we simplify the expressions inside absolute value bars first just like we do with parentheses.
Try it!
Simplify: 
.
Solution (click to reveal)
| Steps | Algebraic |
| Example | 24 − |19 − 3(6 − 2)| |
| Work inside parentheses first: subtract 2 from 6 to get | 24 − |19 − 3(4)| |
| Multiply 3(4) | 24 − |19 − 12| |
| Subtract inside the absolute value bars. | 24 − |7| |
| Take the absolute value. | 24 − 7 |
| Subtract. | 17 |
Simplify Expressions and Order of Operations
What is the difference in English between a phrase and a sentence? A phrase expresses a single thought that is incomplete by itself, but a sentence makes a complete statement. A sentence has a subject and a verb. In algebra, we have expressions and equations.
An expression is a number, a variable, or a combination of numbers and variables using operation symbols. See the examples in the table below.
| Expression | Words | English Phrase |
|---|---|---|
| 3 + 5 | 3 plus 5 | the sum of three and five |
| n − 1 | n minus one | the difference of n and one |
| 6 · 7 | 6 times 7 | the product of six and seven |
 |
x divided by y | the quotient of x and y |
An equation is two expressions linked by an equal sign. When you read the words the symbols represent in an equation, you have a complete sentence in English. The equal sign gives the verb. See the examples in the table below.
| Equation | English Phrase |
|---|---|
| 3 + 5 = 8 | the sum of three and five is equal to eight. |
| n − 1 = 14 | the difference of n and one equals fourteen. |
| 6 · 7 = 42 | the product of six and seven is equal to forty-two. |
| x = 53 |
x is equal to fifty-three. |
| y + 9 = 2y − 3 | y plus nine is equal to two y minus three. |
To simplify an expression means to do all the math possible. For example, to simplify 4 · 2 + 1 we would first multiply 4 · 2 to get 8 and then add the 1 to get 9. A good habit to develop is to work down the page, writing each step of the process below the previous step. This example is illustrated below.
4 · 2 + 1
8 + 1
9
By not using an equal sign when you simplify an expression, you may avoid confusing expressions with equations.
To simplify an expression, do all operations in the expression.
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values.
For example, consider the expression 4 + 3 · 7. Some students simplify this getting 49, by adding 4 + 3 and then multiplying that result by 7. Others get 25, by multiplying 3 · 7 first and then adding 4.
The same expression should give the same result. So mathematicians established some guidelines that are called the order of operations.
How to use the order of operations.
-
- Parentheses and Other Grouping Symbols
-
- Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
-
- Exponents
-
- Simplify all expressions with exponents.
-
- Multiplication and Division
-
- Perform all multiplication and division in order from left to right. These operations have equal priority.
-
- Addition and Subtraction
-
- Perform all addition and subtraction in order from left to right. These operations have equal priority.
-
- Parentheses and Other Grouping Symbols
Students often ask, “How will I remember the order?” The table below has a way to help you remember: Take the first letter of each key word and substitute the silly phrase “Please Excuse My Dear Aunt Sally”.
| Letter description | Algebra equivalent |
| Please | Parentheses |
| Excuse | Exponents |
| My Dear | Multiplication and Division |
| Aunt Sally | Addition and Subtraction |
It’s good that “My Dear” goes together, as this reminds us that multiplication and division have equal priority. We do not always do multiplication before division or always do division before multiplication. We do them in order from left to right.
Similarly, “Aunt Sally” goes together and so reminds us that addition and subtraction also have equal priority and we do them in order from left to right.
Try it!
Simplify: 18 ÷ 6 + 4(5 − 2).
Solution (click to reveal)
| Steps | Algebraic |
| Parentheses? Yes, subtract first. | 18 ÷ 6 + 4(5 − 2). |
| Exponents? No. | 18 ÷ 6 + 4(3) |
| Multiplication or division? | Yes. |
| Divide first because we multiply and divide left to right. | 3 + 4(3) |
| Any other multiplication or division? | Yes. |
| Multiply. | 3 + 12 |
| Any other multiplication of division? | No. |
| Any addition or subtraction? | Yes. |
| Add. | 15 |
When there are multiple grouping symbols, we simplify the innermost parentheses first and work outward.
Try it!
Simplify: 5 + 23 + 3[6 − 3(4 − 2)].
Solution (click to reveal)
| Steps | Algebraic |
| Example | 5 + 23 + 3[6 − 3(4 − 2)] |
| Are there any parentheses (or other grouping symbols)? Yes. |
5 + 23 + 3[6 − 3(4 − 2)] |
| Focus on the parentheses that are inside the brackets. Subtract. |
5 + 23 + 3[6 − 3(2)] |
| Continue inside the brackets and multiply. | 5 + 23 + 3[6 − 6] |
| Continue inside the brackets and subtract.
The expression inside the brackets requires |
5 + 23 + 3[0] |
| Are there any exponents? Yes. Simplify exponents. | 5 + 8 + 3[0] |
| Is there any multiplication or division? Yes. | Yes. |
| Multiply. | 5 + 8 + 0 |
| Is there any addition of subtraction? | Yes. |
| Add. | 13 + 0 |
| Add. | 13 |
Simplify: 9 + 53 − [4(9 + 3)].
Solution (click to reveal)
| Steps | Algebraic |
| Example | 9 + 53 − [4(9 + 3)] |
| Are there any parentheses (or other grouping symbols)? Yes. |
9 + 53 − [4(9 + 3)] |
| Focus on the parentheses that are inside the brackets. Add. | 9 + 53 − [4(12)] |
| Continue inside the brackets and multiply. | 9 + 53 − 48 |
| Are there any exponents? Yes. Simplify exponents. | 9 + 125 − 48 |
| Is there any multiplication or division? No | No |
| Is there any addition of subtraction? | Yes |
| Add | 134 – 48 |
| Subtract | 86 |
Simplify: a. (−2)4 b. -24
Solution A (click to reveal)
Notice the difference in parts (a) and (b). In part (a), the exponent means to raise what is in the parentheses, the −2 to the 4th power. In part (b), the exponent means to raise just the 2 to the 4th power and then take the opposite.
a.
| Steps | Algebraic |
| Example | (−2)4 |
| Write in expanded form | (−2)(−2)(−2)(−2) |
| Multiply | 4(−2)(−2) |
| Multiply | −8(−2) |
| Multiply | 16 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Example | -24 |
| Write in expanded form. We are asked to find the opposite of 24. | −(2 · 2 · 2 · 2) |
| Multiply. | −(4 · 2 · 2) |
| Multiply. | −(8 · 2) |
| Multiply. | -16 |
The last example showed us the difference between (−2)4 and −24. This distinction is important to prevent future errors. The next example reminds us to multiply and divide in order left to right.
Try it!
Simplify: a. 8(−9) ÷ (−2)3. b. −30 ÷ 2 + (−3)(−7).
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Example | 8(−9) ÷ (−2)3 |
| Exponents first. | 8(−9) ÷ (−8) |
| Multiply. | -72 ÷ (−8) |
| Divide. | 9 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Example | −30 ÷ 2 + (−3)(−7) |
| Multiply and divide left to right, so divide first | −15 + (−3)(−7) |
| Multiply. | −15 + 21 |
| Add. | 6 |
Identify and Combine Like Terms
Algebraic expressions are made up of terms. What do you think 3x + 6x would simplify to? If you thought 9x, you would be right!
![\[ \underbrace{x + x + x}_{3x} \ +\ \underbrace{x + x + x + x + x + x}_{6x} \ =\ 9x \]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b60931139f83b19086a70b1a19ea55b3_l3.png "Rendered by QuickLaTeX.com")
A term is a constant or the product of a constant and one or more variables.
Examples of terms are 7, y, 5x2, 9a, and b5.
The coefficient of a term is the constant that multiplies the variable in a term.
Think of the coefficient as the number in front of the variable. The coefficient of the term 3x is 3. When we write x, the coefficient is 1, since x = 1 · x.
Some terms share common traits. When two terms are constants or have the same variable and exponent, we say they are like terms.
Look at the following 6 terms. Which ones seem to have traits in common?
We say,
7 and 4 are like terms.
5x and 3x are like terms.
n2 and 9n2 are like terms.
Terms that are either constants or have the same variables raised to the same powers are called like terms.
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add or subtract the coefficients and keep the same variable for each group of like terms.
If there are like terms in an expression, you can simplify the expression by combining the like terms. We add the coefficients and keep the same variable. See the example in the table below.
| Steps | Algebraic |
| Simplify | 4x + 7x + x |
| Add the coefficients | 12x |
Try it!
Simplify: 2x2 + 3x + 7 + x2 + 4x + 5.
Solution (click to reveal)
| Steps | Algebraic |
| Identify the like terms |
|
| Rearrange the expression so the like terms are together. |
|
| Combine the like terms |  |
Simplify: 3x2 + 7x + 9 + 7x2 + 9x + 8.
Solution (click to reveal)
| Steps | Algebraic |
| Identify the like terms |
|
| Rearrange the expression so the like terms are together. |
|
| Combine the like terms |  |
Evaluate Variable Expressions with Integers
In the last few examples, we simplified expressions using the order of operations. Now we’ll evaluate some expressions—again following the order of operations. To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression means to find the value of the expression when the variable is replaced by a given number.
To evaluate an expression, substitute that number for the variable in the expression and then simplify the expression.
Try it!
Evaluate when x = 4: a. x2 b. 3x c. 2x2 + 3x + 8.
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Example | x2 |
| Replace x with 4 | 42 |
| Use definition of exponent. | 4 · 4 |
| Simplify. | 16 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Example | 3x |
| Replace x with 4 | 34 |
| Use definition of exponent. | 3 · 3 · 3 · 3 |
| Simplify. | 81 |
Solution C (click to reveal)
c.
| Steps | Algebraic |
| Example | 2x2 + 3x + 8 |
| Replace x with 4 | 2(4)2 + 3(4) + 8 |
| Follow the order of operations | 2(16) + 3(4) + 8 |
| Simplify. | 32 + 12 + 8 |
| Solution | 52 |
Evaluate when x = 3, a. x2 b. 4x c. 3x2 + 4x + 1.
Solution A (click to reveal)
| Steps | Algebraic |
| Example | x2 |
| Replace x with 3 | 32 |
| Use definition of exponent. | 3 · 3 |
| Simplify. | 9 |
Solution B (click to reveal)
| Steps | Algebraic |
| Example | 4x |
| Replace x with 3 | 43 |
| Use definition of exponent. | 4 · 4 · 4 |
| Simplify. | 64 |
Solution C (click to reveal)
| Steps | Algebraic |
| Example | 3x2 + 4x + 1 |
| Replace x with 3 | 3(3)2 + 4(3) + 1 |
| Use definition of exponent. | 3(9) + 4(3) + 1 |
| Simplify. | 40 |
Remember that to evaluate an expression means to substitute a number for the variable in the expression. Now we can use negative numbers as well as positive numbers.
Try it!
Evaluate 4x2 − 2xy + 3y2 when x = 2, y = −1.
Solution (click to reveal)
| Steps | Algebraic |
| Example | 4x2 − 2xy + 3y2 |
| Substitute x = 2, y = -1. Use parentheses to show multiplication | 4(2)2 − 2(2)(-1) + 3(-1)2 |
| Simplify exponents. | 4 · 4 – (-4) + 3 · 1 |
| Multiply. | 16 – (-4) + 3 |
| Subtract. | 20 + 3 |
| Add. | 23 |
Properties of Real Numbers
We have already described numbers as counting numbers, whole numbers, and integers. What is the difference between these types of numbers? Difference could be confused with subtraction. How about asking how we distinguish between these types of numbers? See the table below for an example.
| Description | Algebraic |
| Counting numbers | 1, 2, 3, 4, ….. |
| Whole numbers | 0, 1, 2, 3, 4, …. |
| Integers | …., −3, −2, −1, 0, 1, 2, 3, …. |
What type of numbers would we get if we started with all the integers and then included all the fractions? The numbers we would have form the set of rational numbers. A rational number is a number that can be written as a ratio of two integers.
In general, any decimal that ends after a number of digits (such as 7.3 or −1.2684) is a rational number. We can use the place value of the last digit as the denominator when writing the decimal as a fraction. The decimal for 
is the number 
. The bar over the 3 indicates that the number 3 repeats infinitely. Continuously has an important meaning in calculus. The number(s) under the bar is called the repeating block and it repeats continuously.
Since all integers can be written as a fraction whose denominator is 1, the integers (and so also the counting and whole numbers) are rational numbers.
A rational number is a number that can be written both as a ratio of integers 
where p and q are integers and q ≠ 0, and as a decimal that stops or repeats.
Its decimal form stops or repeats.
Are there any decimals that do not stop or repeat? Yes! The number π (the Greek letter pi, pronounced “pie”), which is very important in describing circles, has a decimal form that does not stop or repeat. We use three dots (…) to indicate the decimal does not stop or repeat.
The square root of a number that is not a perfect square is a decimal that does not stop or repeat.
An irrational number is a number that cannot be written as the ratio of two integers. i.e. A number whose decimal form does not stop or repeat cannot be written as a fraction of integers. We call this an irrational number.
Let’s summarize a method we can use to determine whether a number is rational or irrational.
If the decimal form of a number
- repeats or stops, the number is a rational number.
- does not repeat and does not stop, the number is an irrational number.
We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers. The irrational numbers are numbers whose decimal form does not stop and does not repeat. When we put together the rational numbers and the irrational numbers, we get the set of real numbers.
A real number is a number that is either rational or irrational.
Later in this course we will introduce numbers beyond the real numbers. The image below illustrates how the number sets we’ve used so far fit together.
Does the term “real numbers” seem strange to you? Are there any numbers that are not “real,” and, if so, what could they be? Can we simplify 
? Is there a number whose square is −25?
None of the numbers that we have dealt with so far has a square that is −25. Why? Any positive number squared is positive. Any negative number squared is positive. So we say there is no real number equal to . The square root of a negative number is not a real number.
Try it!
Given the numbers 
, list the a. whole numbers b. integers c. rational numbers d. irrational numbers e. real numbers.
Solution (click to reveal)
a. Remember, whole numbers are 0, 1, 2, 3, …, so 8 is the only whole number given.
b. Integers are whole numbers and their opposites (which includes 0). So the whole number 8 is an integer, and −7 is the opposite of a whole number so it is an integer, too. Also, notice that 64 is the square of 8 so –
-8. So the integers are −7, 8, and –
.
c. Since all integers are rational, then −7, 8, and – are rational. Rational numbers also include fractions and decimals that repeat or stop, so 
and 5.9 are rational. So the list of rational numbers is –
, and –.
d. Remember that 5 is not a perfect square, so 
is irrational.
e. All the numbers listed are real numbers.
Using Commutative and Associative Properties
The order we add two numbers doesn’t affect the result. If we add 8 + 9 or 9 + 8, the results are the same—they both equal 17. So, 8 + 9 = 9 + 8. The order in which we add does not matter!
Similarly, when multiplying two numbers, the order does not affect the result. If we multiply 9 · 8 or 8 · 9 the results are the same—they both equal 72. So, 9 · 8 = 8 · 9. The order in which we multiply does not matter!
These examples illustrate the Commutative Property.
| Property | Description |
| of Addition | If a and b are real numbers, then a + b = b + a. |
| of Multiplication | If a and b are real numbers, then a · b = b · a. |
The Commutative Property has to do with order. We subtract 9 − 8 and 8 − 9, and see that 9 − 8 ≠ 8 − 9. Since changing the order of the subtraction does not give the same result, we know that subtraction is not commutative.
Division is not commutative either. Since 12 ÷ 3 ≠ 3 ÷ 12, changing the order of the division did not give the same result. The commutative properties apply only to addition and multiplication! Subtraction and division are not commutative.
When adding three numbers, changing the grouping of the numbers gives the same result. For example, (7 + 8) + 2 = 7 + (8 + 2), since each side of the equation equals 17.
This is true for multiplication, too. For example, 
, since each side of the equation equals 5.
These examples illustrate the Associative Property.
| Property |
Description |
| of Addition | If a, b, and c are real numbers,
then (a + b) + c = a + (b + c). |
| of Multiplication | If a, b, and c are real numbers,
then (a · b) · c = a · (b · c). |
The Associative Property has to do with grouping. If we change how the numbers are grouped, the result will be the same. Notice it is the same three numbers in the same order—the only difference is the grouping.
We saw that subtraction and division were not commutative. They are not associative either. See the examples in the table below.
| Ex. 1 | Ex. 2 |
| (10 − 3) − 2 ≠ 10 − (3 − 2) | (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2) |
| 7 − 2 ≠ 10 − 1 | 6 ÷ 2 ≠ 24 ÷ 2 |
| 5 ≠ 9 | 3 ≠ 12 |
When simplifying an expression, it is always a good idea to plan what the steps will be. In order to combine like terms in the next example, we will use the Commutative Property of addition to write the like terms together.
Try it!
Simplify: 18p + 6q + 15p + 5q.
Solution (click to reveal)
| Steps | Algebraic |
| Example | 18p + 6q + 15p + 5q |
| Use the Commutative Property of addition to reorder so that like terms are together. | 18p + 15p + 6q + 5q |
| Add like terms. | 33p + 11q |
Simplify: 23r + 14s + 9r + 15s.
Solution (click to reveal)
When we have to simplify algebraic expressions, we can often make the work easier by applying the Commutative Property or Associative Property first.
Try it!
Simplify: 
.
Solution (click to reveal)
| Steps | Algebraic |
| Example | |
| Notice that the last 2 terms have a common denominator, so change the grouping. |  |
| Add in parentheses first. |  |
| Simplify the fraction. |  |
| Add. |  |
| Convert to an improper fraction. |  |
Identity, Inverse, and Zero Properties
What happens when we add 0 to any number? Adding 0 doesn’t change the value. For this reason, we call 0 the additive identity. The Identity Property of Addition states that for any real number a, a + 0 = a and 0 + a = a.
What happens when we multiply any number by one? Multiplying by 1 doesn’t change the value. So we call 1 the multiplicative identity. The Identity Property of Multiplication states that for any real number a, a · 1 = a and 1 · a = a.
| Property |
Description |
| of Addition
0 is the additive identity |
For any real number a: a + 0 = a 0 + a = a |
| of Multiplication
1 is the multiplicative identity |
For any real number a: a · 1 = a 1 · a = a |
We call −a the additive inverse of a. The opposite of a number is its additive inverse. A number and its opposite add to zero, which is the additive identity. This leads to the Inverse Property of Addition that states for any real number a, a + (−a) = 0.
What number multiplied by 
gives the multiplicative identity, 1? In other words, times what results in 1? We know
We call 
the multiplicative inverse of a. The reciprocal of a number is its multiplicative inverse. This leads to the Inverse Property of Multiplication that states that for any real number 
.
| Property |
Description |
| of Addition | For any real number a, a + (−a) = 0 −a is the additive inverse of a A number and its opposite add to zero. |
| of Multiplication | For any real number . is the multiplicative inverse of a.A number and its reciprocal multiply to one. |
The Identity Property of addition says that when we add 0 to any number, the result is that same number. What happens when we multiply a number by 0? Multiplying by 0 makes the product equal zero.
What about division involving zero? What is 0 ÷ 3? Think about a real example: If there are no cookies in the cookie jar and 3 people are to share them, how many cookies does each person get? There are no cookies to share, so each person gets 0 cookies. So, 0 ÷ 3 = 0.
We can check division with the related multiplication fact. So we know 0 ÷ 3 = 0 because 0 · 3 = 0.
Now think about dividing by zero. What is the result of dividing 4 by 0? Think about the related multiplication fact:
4 ÷ 0 = ? means ? · 0 = 4
Is there a number that multiplied by 0 gives 4? Since any real number multiplied by 0 gives 0, there is no real number that can be multiplied by 0 to obtain 4. We conclude that there is no answer to 4 ÷ 0 and so we say that division by 0 is undefined.
| Algebraic |
Description |
| a · 0 = 0 0 · a = 0 | The product of any number and 0 is 0. |
| Algebraic |
Description |
 |
Zero divided by any real number, except itself, is zero. |
 is undefined |
Division by zero is undefined. |
Try it!
Simplify: −84n + (−73n) + 84n
Solution (click to reveal)
| Steps | Algebraic |
| Example | −84n + (−73n) + 84n |
| Notice that the first and third terms are opposites; use the Commutative Property of addition to re-order the terms. | −84n + 84n + (−73n) |
| Add left to right. | 0 + (−73n) |
| Add. | −73n |
Simplify: −27a + (−48a) + 27a.
Solution (click to reveal)
−48a
Now we will see how recognizing reciprocals is helpful. Before multiplying left to right, look for reciprocals—their product is 1.
Try it!
Simplify: 
.
Solution (click to reveal)
| Steps | Algebraic |
| Example | |
| Notice the first and third terms are reciprocals, so use the Commutative Property of multiplication to re-order the factors. |  |
| Multiply left to right. |  |
| Multiply. |  |
The next example makes us aware of the distinction between dividing 0 by some number or some number being divided by 0.
Try it!
Simplify: a. 
. b. 
.
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Example |  |
| Zero divided by any real number except itself is 0 | 0 |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Example |  |
| Division by 0 is undefined | undefined |
Simplify: a. 
. b. 
.
Solution A (click to reveal)
a. 0
Solution B (click to reveal)
b. undefined
Distributive Property
Suppose that three friends are going to the movies. They each need $9.25—that’s 9 dollars and 1 quarter—to pay for their tickets. How much money do they need all together?
You can think about the dollars separately from the quarters. They need 3 times $9 so $27 and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.
If a, b, and c are real numbers, then
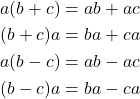
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions.
Try it!
Simplify: 3(x + 4).
Solution (click to reveal)
| Steps | Algebraic |
| Example | 3(x + 4) |
| Distribute. | 3 · x + 3 · 4 |
| Multiply. | 3x + 12 |
Simplify: 4(x + 2).
Solution (click to reveal)
4x + 8
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in the first example above would look like this:
Try it!
Simplify: 
.
Solution (click to reveal)
| Steps | Algebraic |
| Example | |
| Distribute |  |
| Multiply |  |
Using the Distributive Property as shown in the next example will be very useful when we solve money applications in later chapters.
Try it!
Simplify: 100(0.3 + 0.25q).
Solution (click to reveal)
| Steps | Algebraic |
| Example |  |
| Distribute. |  |
| Multiply. |  |
When we distribute a negative number, we need to be extra careful to get the signs correct!
Try it!
Simplify: −11(4 − 3a).
Solution (click to reveal)
| Steps | Algebraic |
| Example | −11(4 − 3a) |
| Distribute. | −11 · 4 − (−11) · 3a |
| Multiply. | −44 − (−33a) |
| Simplify. | −44 + 33a |
Notice that you could also write the result as 33a − 44. Do you know why?
In the next example, we will show how to use the Distributive Property to find the opposite of an expression.
Try it!
Simplify: −(y + 5).
Solution (click to reveal)
| Steps | Algebraic |
| Example | −(y + 5) |
| Multiplying by −1 results in the opposite | −1(y + 5) |
| Distribute. | −1 · y + (−1) · 5 |
| Simplify. | −y + (−5) |
| Simplify. | −y − 5 |
Simplify: −(x − 4).
Solution (click to reveal)
−x + 4
There will be times when we’ll need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be to multiply using the Distributive Property, which removes the parentheses. The next two examples will illustrate this.
Try it!
Simplify: 8 − 2(x + 3)
Solution (click to reveal)
We follow the order of operations. Multiplication comes before subtraction, so we will distribute the 2 first and then subtract.
| Steps | Algebraic |
| Example | 8 − 2(x + 3) |
| Distribute. | 8 − 2 · x − 2 · 3 |
| Multiply. | 8 − 2x − 6 |
| Combine like terms. | −2x + 2 |
Simplify: 4(x − 8) − (x + 3).
Solution (click to reveal)
| Steps | Algebraic |
| Example | 4(x − 8) − (x + 3) |
| Distribute. | 4x − 32 − x − 3 |
| Combine like terms. | 3x − 35 |
All the properties of real numbers we have used in this chapter are summarized in the table below.
| Property |
Algebraic and Descriptive |
| Commutative Property Summary | When adding or multiplying, changing the order gives the same result |
| Commutative Property of addition If a, b are real numbers, then | a + b = b + a |
| Commutative Property of multiplication If a, b are real numbers, then | a · b = b · a |
| Associative Property Summary | When adding or multiplying, changing the grouping gives the same result. |
| Associative Property of addition: If a, b, and c are real numbers, then | (a + b) + c = a + (b + c) |
| Associative Property of multiplication: If a, b, and c are real numbers, then | (a · b) · c = a · (b · c) |
| Distributive Property Summary | If a, b, and c are real numbers, then |
| Distributive Property ex. 1 | a(b + c) = ab + ac |
| Distributive Property ex. 2 | (b + c)a = ba + ca |
| Distributive Property ex. 3 | a(b − c) = ab − ac |
| Distributive Property ex. 4 | (b − c)a = ba − ca |
| Identity Property Summary | See each below |
| Identity Property of addition: For any real number a, 0 is the additive identity |
a + 0 = a or 0 + a = a |
| Identity Property of multiplication: For any real number a, 1 is the multiplicative identity |
a · 1 = a or 1 · a = a |
| Inverse Property | See each below |
| Inverse Property of addition: For any real number a, −a is the additive inverse of a | a + (−a) = 0, A number and its opposite add to zero. |
| Inverse Property of multiplication: For any real number a, a ≠ 0. is the multiplicative inverse of a |
 . A number and its reciprocal multiply to one. |
| Properties of Zero | See each below |
| Multiplication by Zero: For any real number a, | a · 0 = 0 or 0 · a = 0 |
| Division by Zero: For any real number a, a ≠ 0 |  |
| Division by Zero ex. 2: For any real number a, |  is undefined |
Key Concepts
- Opposite Notation
−a means the opposite of the number a
The notation −a is read as “the opposite of a.” - Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as |n| and |n| ≥ 0 for all numbers.
Absolute values are always greater than or equal to zero
- Grouping Symbols
Parentheses ( ) Braces { }
Brackets [ ] Absolute value | | - Subtraction Property
a − b = a + (−b)
Subtracting a number is the same as adding its opposite. - Multiplication and Division of Signed Numbers
For multiplication and division of two signed numbers:
| Same signs | Result |
|---|---|
| • Two positives | Positive |
| • Two negatives | Positive |
If the signs are the same, the result is positive.
| Different signs | Result |
|---|---|
| • Positive and negative | Negative |
| • Negative and positive | Negative |
If the signs are different, the result is negative.
- Multiplication by -1
−1a = −a
Multiplying a number by −1 gives its opposite. - How to Use Integers in Applications.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
| Property |
Algebraic and Descriptive |
| Commutative Property Summary | When adding or multiplying, changing the order gives the same result |
| Commutative Property of addition If a, b are real numbers, then | a + b = b + a |
| Commutative Property of multiplication If a, b are real numbers, then | a · b = b · a |
| Associative Property Summary | When adding or multiplying, changing the grouping gives the same result. |
| Associative Property of addition: If a, b, and c are real numbers, then | (a + b) + c = a + (b + c) |
| Associative Property of multiplication: If a, b, and c are real numbers, then | (a · b) · c = a · (b · c) |
| Distributive Property Summary | If a, b, and c are real numbers, then |
| Distributive Property ex. 1 | a(b + c) = ab + ac |
| Distributive Property ex. 2 | (b + c)a = ba + ca |
| Distributive Property ex. 3 | a(b − c) = ab − ac |
| Distributive Property ex. 4 | (b − c)a = ba − ca |
| Identity Property Summary | See each below |
| Identity Property of addition: For any real number a, 0 is the additive identity |
a + 0 = a or 0 + a = a |
| Identity Property of multiplication: For any real number a, 1 is the multiplicative identity |
a · 1 = a or 1 · a = a |
| Inverse Property | See each below |
| Inverse Property of addition: For any real number a, −a is the additive inverse of a | a + (−a) = 0, A number and its opposite add to zero. |
| Inverse Property of multiplication: For any real number a, a ≠ 0. is the multiplicative inverse of a |
. A number and its reciprocal multiply to one. |
| Properties of Zero | See each below |
| Multiplication by Zero: For any real number a, | a · 0 = 0 or 0 · a = 0 |
| Division by Zero: For any real number a, a ≠ 0 | |
| Division by Zero ex. 2: For any real number a, | is undefined |
- Derived from Openstax Intermediate Algebra; Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction . Pre-algebra; Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵
Topics Covered:[1]
Recognize the Graph of a Quadratic Function
Previously we very briefly looked at the function [latex]\displaystyle f(x) = x^2[/latex], which we called the square function. It was one of the first non-linear functions we looked at. Now we will graph functions of the form [latex]\displaystyle f(x) = a x^2+ bx + c[/latex] if [latex]\displaystyle a\ne 0[/latex]. We call this kind of function a quadratic function.
Quadratic Function
A quadratic function, where a, b, and c are real numbers and [latex]\displaystyle a\ne 0[/latex], is a function of the form
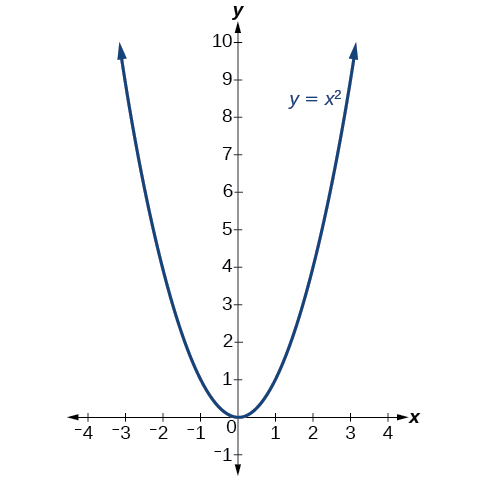
We graphed the quadratic function [latex]\displaystyle f(x) = x^2[/latex] by plotting points.
| x | f(x) = x2 | (x , f(x)) |
| -3 | 9 | (-3, 9) |
| -2 | 4 | (-2, 4) |
| -1 | 1 | (-1, 1) |
| 0 | 0 | (0, 0) |
| 1 | 1 | (1, 1) |
| 2 | 4 | (2, 4) |
| 3 | 9 | (3, 9) |
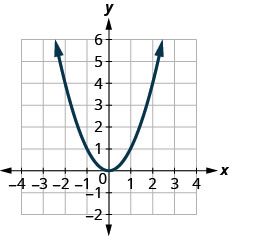
Every quadratic function has a graph that looks like this. We call this figure a parabola. Let’s practice graphing a parabola by plotting a few points.
Try it!
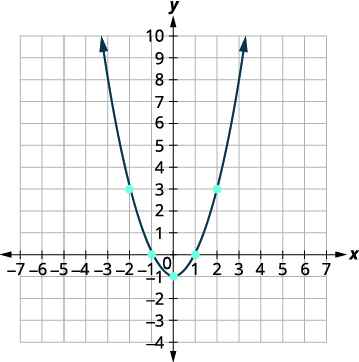
Graph [latex]\displaystyle f(x)=x^2 - 1[/latex]
Solution (click to reveal)
We will graph the function by plotting points.
Step 1: Choose integer values for x, substitute them into the equation and simplify to find [latex]\displaystyle f(x)[/latex]. Record the values of the ordered pairs in the chart.
| x | f(x) |
| 0 | -1 |
| 1 | 0 |
| -1 | 0 |
| 2 | 3 |
| 2 | 3 |
Step 2: Plot the points, and then connect them with a smooth curve. The result will be the graph of the function [latex]\displaystyle f(x)=x^2 - 1[/latex]
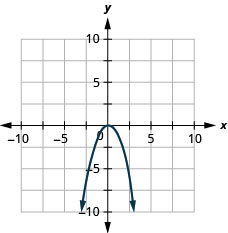
Graph [latex] f(x) = -x^2[/latex].
Solution (click to reveal)
The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry. These features are illustrated in the graph below.
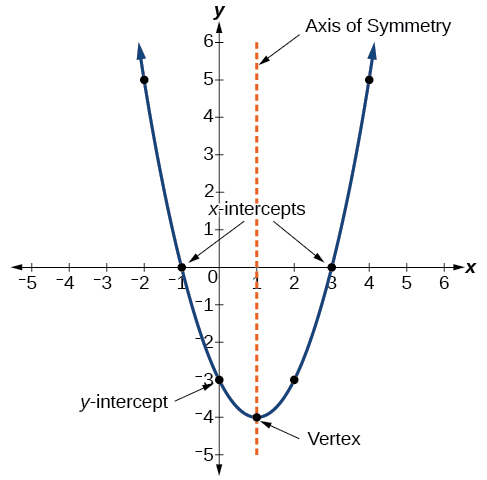
The y-intercept is the point at which the parabola crosses the y-axis. The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the x-intercepts represent the zeros, or roots of the quadratic function, the values of x at which y = 0.
Try it! - Identifying the Characteristics of a Parabola
Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown in the graph below.
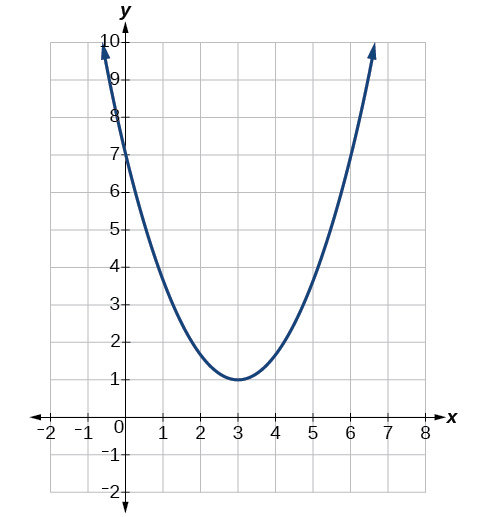
Solution (click to reveal)
The vertex is the turning point of the graph. We can see that the vertex is at (3, 1). Because this parabola opens upward, the vertex is a minimum point. The axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is x = 3. This parabola does not cross the x-axis, so it has no zeros. It crosses the y-axis at (0, 7), so, this is the y-intercept.
All graphs of quadratic functions of the form f(x) = ax2 + bx + c are parabolas that open upward or downward, as shown in the graph below.
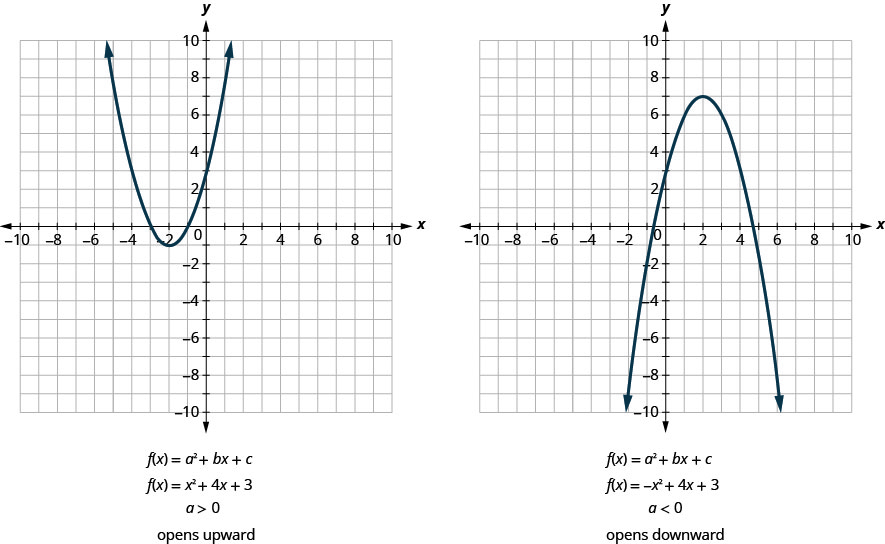
Notice that the only difference in the two functions is the negative sign before the quadratic term (x2 in the equation of the graph above). When the quadratic term is positive, the parabola opens upward, and when the quadratic term is negative, the parabola opens downward.
Parabola Orientation
For the graph of the quadratic function f (x) = ax2 + bx + c, if:
a > 0, the parabola opens upward
a < 0, the parabola opens downward 
Try it!
Determine whether each parabola opens upward or downward:
a. [latex]\displaystyle f(x) = -3x^2 + 2x - 4[/latex]
b. [latex]\displaystyle f(x) = 6x^2 + 7x - 9[/latex].
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Find the value of “a”. | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c} \\ f(x) &= -3x^2 + 2x -4 \\ a &= -3 \end{align*}[/latex] |
| Solution | Since the “a” is negative, the parabola will open downward. |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Find the value of “a”. | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c} \\ f(x) &= 6x^2 + 7x - 9 \\ a &= 6 \end{align*}[/latex] |
| Solution | Since the “a” is positive, the parabola will open upward. |
Determine whether the graph of each function is a parabola that opens upward or downward:
a. [latex]\displaystyle f(x) = 2x^2 + 5x - 2[/latex]
b. [latex]\displaystyle f(x) = -3x^2 - 4x + 7[/latex].
Solution (click to reveal)
a. up
b. down
Find the Axis of Symmetry and Vertex of a Parabola
We will be looking at 2 forms of the quadratic function. The general form of a quadratic function presents the function in the form
f(x) = ax2 + bx +c
where a, b, and c are real numbers and a ≠ 0. If a > 0, the parabola opens upward. If a < 0, the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.
Look again at the previous graph. Do you see that we could fold each parabola in half and then one side would lie on top of the other? The ‘fold line’ is a line of symmetry. We call it the axis of symmetry of the parabola.
We show the same two graphs again with the axis of symmetry below.
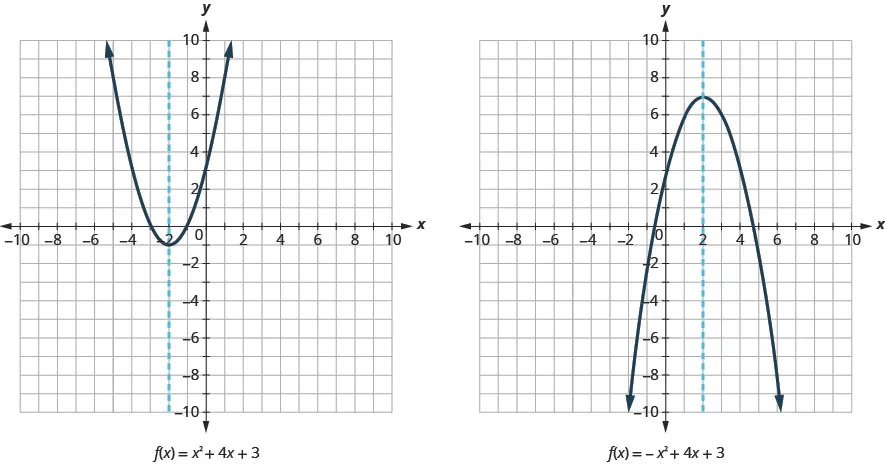
The axis of symmetry is defined by [latex]\displaystyle x= -\frac{b}{2a}[/latex]. If we use the quadratic formula, [latex]\displaystyle x= \frac{-b\pm\sqrt{b^2−-4ac}}{2a}[/latex], to solve ax2 + bx + c = 0 for the x-intercepts or zeros, we find the value of x halfway between them is always [latex]\displaystyle x = -\frac{b}{2a}[/latex], the equation for the axis of symmetry.
So to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula [latex]\displaystyle x = -\frac{b}{2a}[/latex].
| Steps | a >0 Example | a < 0 Example |
| Quadratic form | [latex]\displaystyle f(x) = ax^2 + bx + c[/latex] | [latex]\displaystyle f(x) = ax^2 + bx + c[/latex] |
| Starting Equation | [latex]\displaystyle f(x) = x^2 + 4x + 3[/latex] | [latex]\displaystyle f(x) = -x^2 + 4x + 3[/latex] |
| Axis of Symmetry equation | The axis of symmetry is defined by [latex]\displaystyle x= -\frac{b}{2a}[/latex] | The axis of symmetry is defined by [latex]\displaystyle x= -\frac{b}{2a}[/latex] |
| Plug in the values for a & b into the equation | [latex]\displaystyle x= -\frac{4}{2.1}[/latex] | [latex]\displaystyle x= -\frac{4}{2{(-1)}}[/latex] |
| Simplify | [latex]\displaystyle x= -2[/latex] | [latex]\displaystyle x= 2[/latex] |
Notice that these are the equations of the dashed blue lines on the graphs.
The point on the parabola that is the lowest (parabola opens up), or the highest (parabola opens down), lies on the axis of symmetry. This point is called the vertex of the parabola.
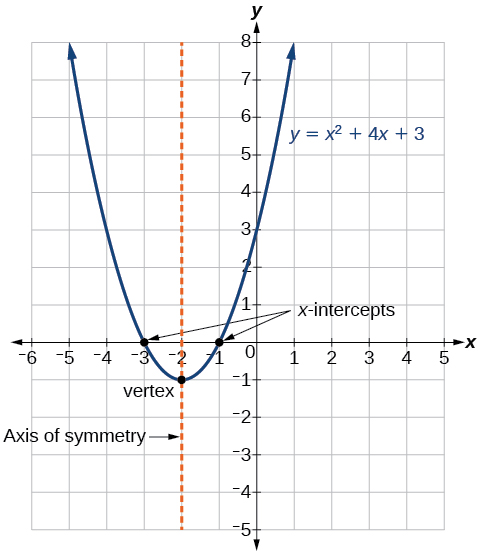We can easily find the coordinates of the vertex because we know it is on the axis of symmetry. This means its x-coordinate is [latex]\displaystyle x = -\frac{b}{2a}[/latex]. To find the y-coordinate of the vertex we substitute the value of the x-coordinate into the quadratic function, as shown in the table below.
| Steps | a >0 Example | a < 0 Example |
| Starting Equation | [latex]\displaystyle f(x) = x^2 + 4x + 3[/latex] | [latex]\displaystyle f(x) = -x^2 + 4x + 3[/latex] |
| Axis of Symmetry (see previous table above) | The axis of symmetry is [latex]\displaystyle x= {\color{myred1}-2}[/latex] | The axis of symmetry is [latex]\displaystyle x= {\color{myred1}2}[/latex] |
| Vertex x-coordinate | The vertex is [latex]\displaystyle({\color{myred1}-2}, \_)[/latex] | The vertex is [latex]\displaystyle({\color{myred1}2}, \_)[/latex] |
| Repeat equation to find the y-coordinate | [latex]\displaystyle f(x) = x^2 + 4x + 3[/latex] | [latex]\displaystyle f(x) = -x^2 + 4x + 3[/latex] |
| Plug in Vertex x-coordinate | [latex]\displaystyle f(x) = ({\color{myred1}-2})^2 + 4({\color{myred1}-2}) + 3[/latex] | [latex]\displaystyle f(x) = -({\color{myred1}2})^2 + 4({\color{myred1}2}) + 3[/latex] |
| Simplify | [latex]\displaystyle f(x) = -1[/latex] | [latex]\displaystyle f(x) = 7[/latex] |
| Solution | The vertex is [latex]\displaystyle(-2, -1)[/latex] | The vertex is [latex]\displaystyle(-2, 7)[/latex] |
Axis of Symmetry and Vertex of a Parabola
The graph of the function f (x) = ax2 + bx + c is a parabola where:
- the axis of symmetry is the vertical line [latex]\displaystyle x = -\frac{b}{2a}[/latex].
- the vertex is a point on the axis of symmetry, so its x-coordinate is [latex]\displaystyle \frac{b}{2a}[/latex].
- the y-coordinate of the vertex is found by substituting [latex]\displaystyle x = -\frac{b}{2a}[/latex] into the quadratic equation.
Try it!
For the graph of f(x) = 3x2 − 6x + 2, find:
a. the axis of symmetry
b. the vertex.
Solution A (click to reveal)
a.
| Steps | Algebraic |
| Equation | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c }\\ f(x) &= 3x^2 - 6x + 2 \end{align*}[/latex] |
| The axis of symmetry is the vertical line [latex]\displaystyle x= -\frac{b}{2a}[/latex].
Substitute the values of a, b into the equation. |
[latex]\displaystyle x = -\frac{-6}{2.3}[/latex] |
| Simplify. | [latex]\displaystyle x = 1[/latex] |
| Solution | The axis of symmetry is the line x = 1. |
Solution B (click to reveal)
b.
| Steps | Algebraic |
| Equation | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c }\\ f(x) &= 3x^2 - 6x + 2 \end{align*}[/latex] |
| The vertex is a point on the line of symmetry, so its x-coordinate will be [latex] \displaystyle x= 1 [/latex].
Find f(1). |
[latex]\displaystyle f(x) = 3{(1)}^2 - 6{(1)} + 2[/latex] |
| Simplify. | [latex]\displaystyle f(x) = 3 . 1 - 6 + 2[/latex] |
| The result is the y-coordinate. | [latex]\displaystyle f(x) = -1[/latex] |
| Solution |
The vertex is (1, -1). |
For the graph of f(x) = 2x2 − 8x + 1, find:
a. the axis of symmetry
b. the vertex.
Solution (click to reveal)
a. x = 2
b. (2, −7)
Earlier in the chapter we mentioned we will see 2 forms of the quadratic function. We have already looked at the general form of the quadratic function; the second form is the Standard form (also called the Vertex form). The standard form of a quadratic function presents the function in the form
where(h, k) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function.
As with the general form, if a > 0, the parabola opens upward, and the vertex is a minimum. If a < 0, the parabola opens downward, and the vertex is a maximum. The graph below represents the graph of the quadratic function written in standard form as y = -3(x + 2)2 + 4. Since x - h = x + 2 in this example, h = -2. In this form, a = -3, h = -2, and k = 4. Because a < 0, the parabola opens downward. The vertex is at (−2, 4).
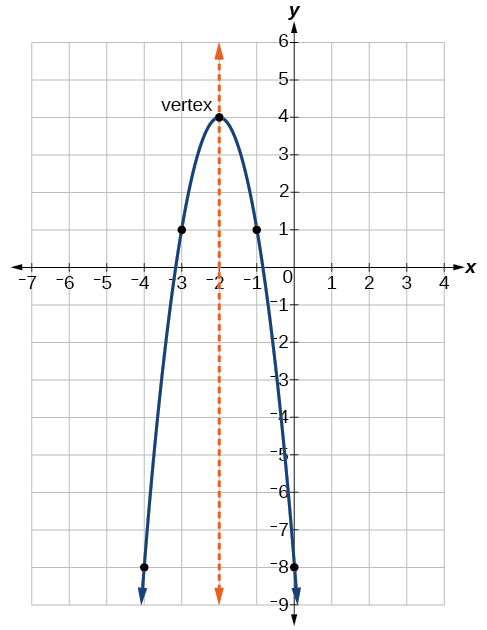
The standard form is useful for determining how the graph is transformed from the graph of y = x2. The graph shown below is that of this basic function.
The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.
For the linear terms to be equal, the coefficients must be equal.
[latex]\displaystyle -2ah = b, \quad \text{ so }\quad h = - \frac{b}{2a}[/latex]
This is the axis of symmetry we defined earlier. Setting the constant terms equal:
[latex]\begin{align*} ah^2 + k &= c \\ k &= c - ah^2\\ &= c - a - \left(\frac{b}{2a}\right)^2\\ &= c - \frac{b^2}{4a} \end{align*}[/latex]
In practice, though, it is usually easier to remember that k is the output value of the function when the input is h, so f(h) = k.
Forms of Quadratic Functions
A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola.
The general form of a quadratic function is f(x) = ax2 + bx + c where a, b, and c are real numbers and a ≠ 0.
The standard form of a quadratic function is f(x) = a(x − h)2 + k where a ≠ 0.
The vertex (h, k) is located at
How to find the vertex of the parabola, given a quadratic function.
- Identify a, b, and c.
- Find h, the x-coordinate of the vertex, by substituting a and b into [latex]\displaystyle h = - \frac{b}{2a}[/latex].
- Find k, the y-coordinate of the vertex, by evaluating [latex] \displaystyle k = f(h) = f \left(-\frac{b}{2a}\right)[/latex].
Try it! - Finding the Vertex of a Quadratic Function
Find the vertex of the quadratic function f(x) = 2x2 – 6x + 7. Rewrite the quadratic in standard form (vertex form).
Solution (click to reveal)
The horizontal coordinate of the vertex will be at
[latex]\begin{align*} h &= - \frac{b}{2a}\\ &= - \frac{-6}{2(2)}\\ &= \frac{6}{4}\\ &= \frac{3}{2} \end{align*}[/latex]
The vertical coordinate of the vertex will be at
[latex]\begin{align*} k &= f(h)\\ &= f\left(\frac{3}{2}\right) \\ &= 2\left(\frac{3}{2}\right) ^2 - 6\left(\frac{3}{2}\right) + 7 \\
&= \frac{5}{2} \end{align*}[/latex]
Rewriting into standard form, the stretch factor will be the same as the a in the original quadratic. First, find the horizontal coordinate of the vertex. Then find the vertical coordinate of the vertex. Substitute the values into standard form, using the "a" from the general form.
The standard form of a quadratic function prior to writing the function then becomes the following:
Given the equation g(x) = 13 + x2 − 6x, write the equation in general form and then in standard form.
Solution (click to reveal)
g(x) = x2 − 6x + 13 in general form; g(x) = (x − 3)2 + 4 in standard form
Find the Intercepts of a Parabola
When we graphed linear equations, we often used the x- and y-intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.
Remember, at the y-intercept the value of x is zero. So to find the y-intercept, we substitute x = 0 into the function.
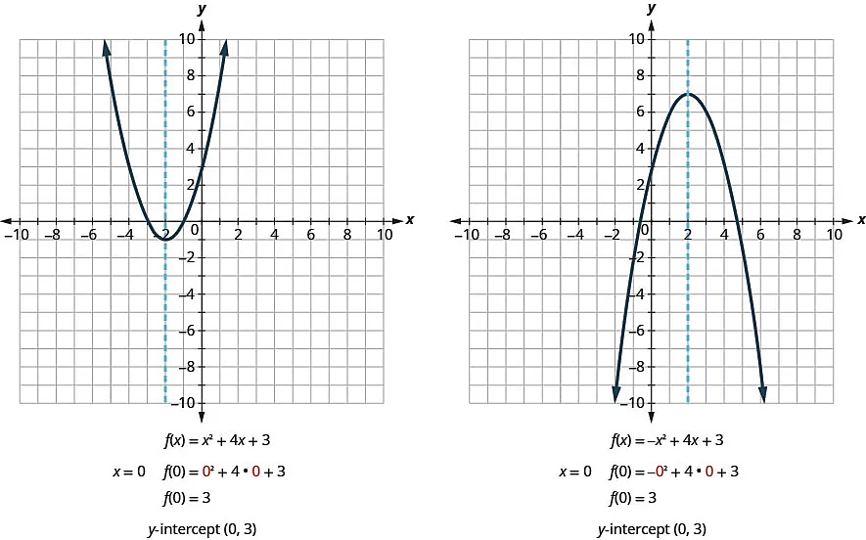
Let’s find the y-intercepts of the two parabolas shown in the graph below.
An x-intercept results when the value of f(x) is zero. To find an x-intercept, we let f(x) = 0. In other words, we will need to solve the equation 0 = ax2 + bx + c for x.
Solving quadratic equations like this is exactly what we have done earlier in this chapter!
We can now find the x-intercepts of the two parabolas we looked at. First we will find the x-intercepts of the parabola whose function is f (x) = x2 + 4x + 3.
| Steps | Algebraic |
| Function | [latex]\displaystyle f(x) = x^2 + 4x + 3[/latex] |
| Let f(x) = 0, as indicated in red. | [latex]\displaystyle {\color{myred1}0} = x^2 + 4x + 3[/latex] |
| Factor. | [latex]\displaystyle 0 = {(x + 1)} {(x + 3)}[/latex] |
| Use the Zero Product Property. | [latex]\begin{align*} {x + 1} &= 0 \\ {x + 3} &= 0 \end{align*}[/latex] |
| Solve. | [latex]\begin{align*} x &= -1 \\ x &= -3 \end{align*}[/latex] |
| Solution | The x-intercepts are (−1, 0) and (−3, 0). |
Now we will find the x-intercepts of the parabola whose function is f (x) = -x2 + 4x + 3.
| Steps | Algebraic |
| Function | [latex]\displaystyle f(x) = -x^2 + 4x + 3[/latex] |
| Let f(x) = 0, as indicated in red. | [latex]\displaystyle {\color{myred1} 0} = -x^2 + 4x + 3[/latex] |
| This quadratic does not factor, so we use the Quadratic Formula. | [latex]\displaystyle x= \frac{-b\pm\sqrt{b^2−-4ac}}{2a}[/latex] |
| Substitute a = −1, b = 4, c = 3 | [latex]\displaystyle x= \frac{-4\pm\sqrt{4^2−-4(-1)(2)}}{2(-1)}[/latex] |
| Simplify | [latex]\begin{align*} x &= \frac{-4 \pm \sqrt{28}}{-2} \\ x &= \frac{-4 \pm 2\sqrt{7}}{-2} \\ x &= \frac{-2(2 \pm \sqrt{7})}{-2} \\ x &= 2 \pm \sqrt{7} \end{align*}[/latex] |
| Solution | The x-intercepts are [latex]\displaystyle (2 + \sqrt{7}, 0)[/latex] and [latex]\displaystyle (2 - \sqrt{7}, 0)[/latex]. |
We will use the decimal approximations of the x-intercepts so that we can locate these points on the graph,
Do these results agree with our graphs? See the graphs below.
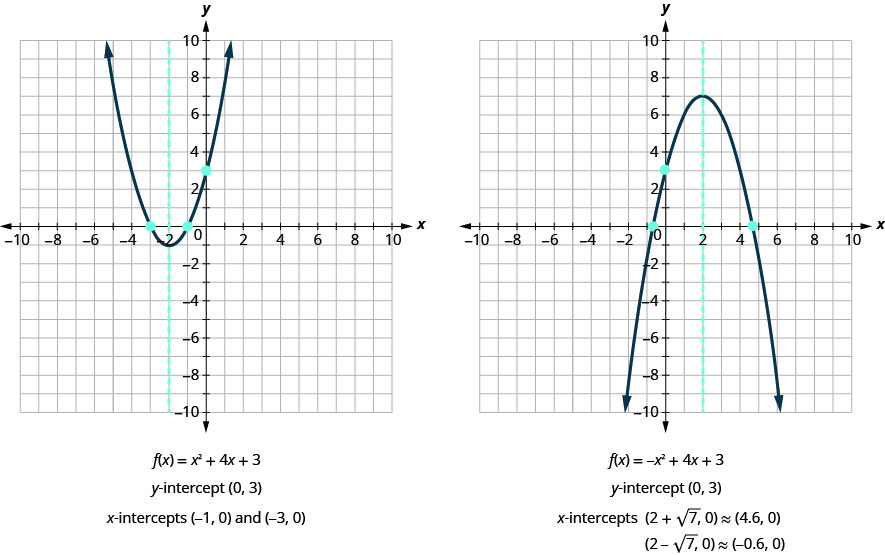
Find the Intercepts of a Parabola
To find the intercepts of a parabola whose function is f(x) = ax2 + bx + c:
| y-intercept | x-intercepts |
| Let x = 0 and solve for f(x). | Let f(x) = 0 and solve for x. |
Try it!
Find the intercepts of the parabola whose function is f(x) = x2 − 2x − 8.
Solution (click to reveal)
| Steps | Algebraic |
| To find the y-intercept, | [latex]\displaystyle f(x) = x^2 - 2x - 8[/latex] |
| let x = 0, as indicated in red. | [latex]\displaystyle f(0) = {\color{myred1}0}^2 - 2({\color{myred1}0}) - 8[/latex] |
| and solve for f(x) | [latex]\displaystyle 0 = - 8[/latex] |
| When x = 0, then f(0) = −8. | The y-intercept is the point (0, −8). |
| To find the x-intercept, | [latex]\displaystyle f(x) = x^2 - 2x - 8[/latex] |
| Set equal to zero | [latex]\displaystyle 0 = x^2 - 2x - 8[/latex] |
| Solve by factoring. | [latex]\displaystyle 0 = {(x - 4)} {(x + 2)}[/latex] |
| Set each factor to zero and solve | [latex]\begin{align*} 0 &= x -4 \\ 0 &= x + 2 \end{align*}[/latex] |
| Solution | [latex]\begin{align*} 4 &= x \\ -2 &= x \end{align*}[/latex] |
| When f(x) = 0, then x = 4 or x = −2. | The x-intercepts are the points (4, 0) and (−2, 0). |
Find the intercepts of the parabola whose function is f(x) = x2 − 4x − 12.
Solution (click to reveal)
y-intercept: (0, −12) x-intercepts (−2, 0), (6, 0)
In this chapter, we have been looking at quadratic functions of the form f(x) = ax2 + bx + c. The graphs of these functions are parabolas. The x-intercepts of the parabolas occur where f(x) = 0.
Let's compare the quadratic equation to the quadratic function for comparison. For example:
| Quadratic equation | Steps | Quadratic function |
| x2 − 2x − 15 = 0 | Equation / Function |
f(x) = x2 − 2x − 15 |
| x2 − 2x − 15 = 0 | Let f(x) = 0 on the function to the right. | 0 = x2 − 2x − 15 |
| (x − 5) (x + 3) = 0 | Factor the equations | 0 = (x − 5) (x + 3) |
| x − 5 = 0 x + 3 = 0 | Simplify | x − 5 = 0 x + 3 = 0 |
| x = 5 x = −3 | Solution | x = 5 x = −3 |
| No further steps | For the function, we represent these as the x-intercepts. |
(5, 0) and (−3, 0) x-intercepts |
The solutions of the quadratic function are the x values of the x-intercepts.
Earlier, we saw that quadratic equations have 2, 1, or 0 solutions. The graphs below show examples of parabolas for these three cases. Since the solutions of the functions give the x-intercepts of the graphs, the number of x-intercepts is the same as the number of solutions.
Previously, we used the discriminant to determine the number of solutions of a quadratic function of the form ax2 + bx + c = 0. Now we can use the discriminant to tell us how many x-intercepts there are on the graph.
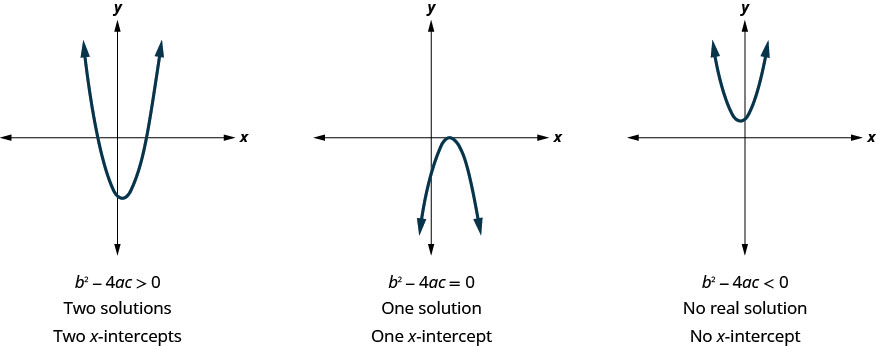
Before you find the values of the x-intercepts, you may want to evaluate the discriminant so you know how many solutions to expect.
Try it!
Find the intercepts of the parabola for the function f(x) = 5x2 + x + 4.
Solution (click to reveal)
| Steps | Algebraic |
| Function | [latex]\displaystyle f(x) = 5x^2 + x + 4[/latex] |
| To find the y-intercept, let x = 0, as indicated in red. | [latex]\displaystyle f(0) = 5.({\color{myred1}0})^2 + {\color{myred1}0} + 4[/latex] |
| Solve for f(x). | [latex]\displaystyle f(0) = 4[/latex] |
| Y-intercept? |
When x = 0, then f(0) = 4. The y-intercept is the point (0, 4). |
| Function - to find the x-intercept | [latex]\displaystyle f(x) = 5x^2 + x + 4[/latex] |
| To find the x-intercept, let f(x) = 0 and solve for x. | [latex]\displaystyle 0 = 5x^2 + x + 4[/latex] |
| Find the value of the discriminant to predict the number of solutions which is also the number of x-intercepts. |
b2 − 4ac 12 − 4 · 5 · 4 1 − 80 −79 |
| X-intercept? | Since the value of the discriminant is negative, there is no real solution to the equation. There are no x-intercepts. |
Find the intercepts of the parabola whose function is f(x) = 3x2 + 4x + 4.
Solution (click to reveal)
y-intercept: (0, 4) no x-intercept
Graph Quadratic Functions Using Properties
Now we have all the pieces we need in order to graph a quadratic function. We just need to put them together. In the next example we will see how to do this.
Try it! - How to Graph a Quadratic Function Using Properties
Graph f(x) = x2 − 6x + 8 by using its properties.
Solution (click to reveal)
| Steps | Algebraic |
| Step 1. Determine whether the parabola opens upward or downward: Look at a in the equation. [latex]\displaystyle f(x) = x^2 - 6x + 8[/latex] | [latex]\begin{gather*} f(x) = x^2 - 6x + 8\\ {\color{myred1}a = 1, b = -6, c = 8}\\\end{gather*} [/latex]
Since a is positive, the parabola opens upward. |
| Step 2. Find axis of symmetry: The axis of symmetry is the line [latex]\displaystyle x = -\frac{b}{2a}[/latex] | [latex]\begin{align*} x &= -\frac{b}{2a} \\ x &= -\frac{(-6)}{2 . 1} \\ x &= 3\end{align*}[/latex]
The axis of symmetry is the line x = 3 |
| Step 3. Find the vertex: The vertex is on the axis of symmetry. So substitute x = 3. | [latex]\begin{align*} f(x) &= x^2 -6x +8 \\ f(3) &= {\color{myred1}(3)}^2 - 6. {\color{myred1}(3)} + 8 \\ f(3) &= -1\end{align*}[/latex]
The vertex is (3, -1). |
| Step 4. Find the y-intercept. Find the point symmetric to the y-intercept across the axis of symmetry:
We find f(0). We use the axis of symmetry to find a point symmetric to the y-intercept. The y-intercept is 3 unit left of the axis of symmetry, x= 3. A point 3 unit to the right of the axis of symmetry has x = 6. |
[latex]\begin{align*} f(x) &= x^2 - 6x + 8 \\ f(0) & = {\color{myred1}(0)}^2 -6.{\color{myred1}0} + 8 \\ f(0) &= 8\end{align*}[/latex]
The y-intercept is (0, 8). Point symmetric to y-intercept: The point is (6, 8). |
| Step 5. Find the x-intercept and find additional points if needed:
We solve f(x) = 0, by factoring. |
[latex]\begin{align*} f(x) &= x^2 - 6x + 8 \\ 0 &= x^2 - 6x + 8 \\ 0 &= (x-2)(x-4) \\ x &= 2 \\ x &=4\end{align*}[/latex]
The x-intercepts are (2, 0) and (4, 0). |
| Step 6. Graph the parabola:
We graph the vertex, intercepts and the point symmetric to the y-intercept. W connect these 5 points to sketch the parabolas. |
 |
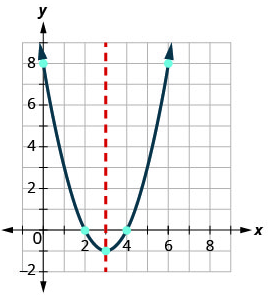Graph f(x) = x2 − 8x + 12 by using its properties.
Solution (click to reveal)
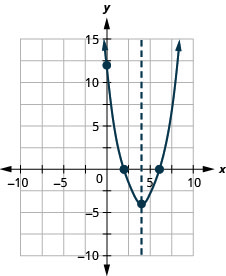
How to graph a quadratic function using properties.
- Determine whether the parabola opens upward or downward.
- Find the equation of the axis of symmetry.
- Find the vertex.
- Find the y-intercept. Find the point symmetric to the y-intercept across the axis of symmetry.
- Find the x-intercepts. Find additional points if needed.
- Graph the parabola.
We were able to find the x-intercepts in a previous example by factoring. We find the x-intercepts in the next example by factoring too.
Try it!
Graph f(x) = -x2 + 6x − 9 by using its properties.
Solution (click to reveal)
| Steps | Algebraic |
| Original Function | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c}\\ f(x) &= -x^2 + 6x - 9 \end{align*}[/latex] |
| Since a = −1, the parabola opens downward. | |
| To find the equation of the axis of symmetry, use [latex]\displaystyle x = -\frac{b}{2a}[/latex] | [latex]\displaystyle x= -\frac{b}{2a}[/latex] |
| Plug-in the values for a and b | [latex]\displaystyle x= -\frac{6}{2(-1)}[/latex] |
| Simplify | [latex]\displaystyle x= 3[/latex] |
| Solution of vertex and axis of symmetry | The axis of symmetry is x = 3 and the vertex is on the line x = 3. |
| Graph the line |  |
| Original Function | [latex]\displaystyle f(x) = -x^2 + 6x - 9[/latex] |
| Find f(3), as indicated in red. | [latex]\displaystyle f(3) = 5. {\color{myred1}3}^2 + 6.{\color{myred1}3} - 9[/latex] |
| Simplify | [latex]\begin{align*} f(3) &= -9 + 18 - 9 \\ f(3) &= 0 \end{align*}[/latex] |
| Solution | The vertex is (3, 0) |
| Graph the Vertex. |  |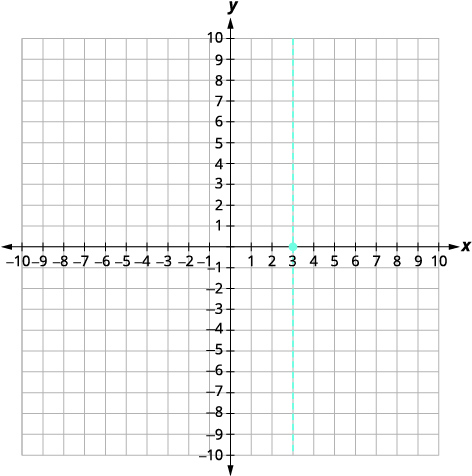
| The y-intercept occurs when x = 0. Find f(0). | [latex]\displaystyle f(x) = -x^2 + 6x - 9[/latex] |
| Substitute x = 0, as indicated in red. | [latex]\displaystyle f(0) = 5. {\color{myred1}0}^2 + 6.{\color{myred1}0} - 9[/latex] |
| Simplify | [latex]\displaystyle f(0) = - 9[/latex] |
| Solution | The y-intercept is (0,−9). |
| The point (0, −9) is three units to the left of the line of symmetry. The point three units to the right of the line of symmetry is (6, −9) and the point symmetric to the y-intercept. |  |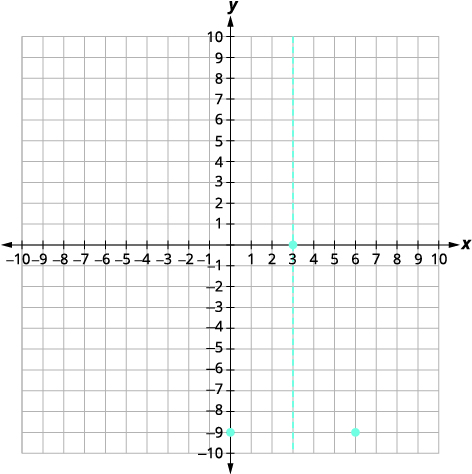
| The x-intercept occurs when f(x) = 0. | [latex]\displaystyle f(x) = -x^2 + 6x - 9[/latex] |
| Find f(x) = 0, as indicated in red. | [latex]\displaystyle {\color{myred1}0} = -x^2 + 6x - 9[/latex] |
| Factor the GCF. | [latex]\displaystyle 0 = (-x^2 + 6x - 9)[/latex] |
| Factor the trinomial. | [latex]\displaystyle 0 = -(x - 3)^2 [/latex] |
| Solve for x. | [latex]\displaystyle x = 3 [/latex] |
| Connect the points to graph the parabola. |  |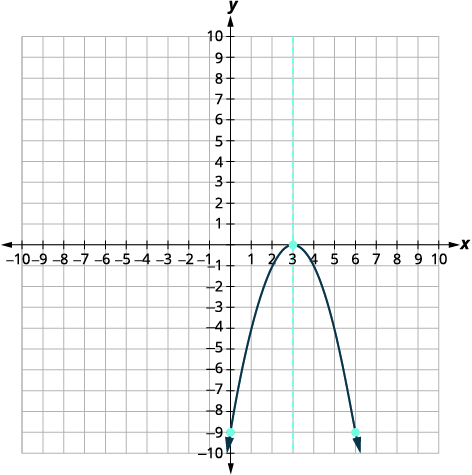
Graph f(x) = 3x2 + 12x − 12 by using its properties.
Solution (click to reveal)
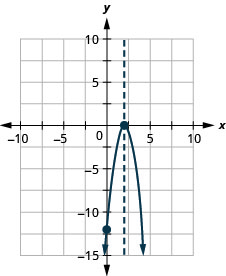
For the graph of f(x) = −x2 + 6x − 9, the vertex and the x-intercept were the same point. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation 0 = −x2 + 6x − 9 is 0, so there is only one solution. That means there is only one x-intercept, and it is the vertex of the parabola.
How many x-intercepts would you expect to see on the graph of f(x) = x2 + 4x + 5?
Try it!
Graph f(x) = x2 + 4x + 5 by using its properties.
Solution (click to reveal)
| Steps | Algebraic |
| Original Function | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c} \\ f(x) &= x^2 + 4x + 5 \end{align*}[/latex] |
| Since a = 1, the parabola opens upward. |  |
| To find the equation of the axis of symmetry, use [latex]\displaystyle x = -\frac{b}{2a}[/latex] | [latex]\displaystyle x= -\frac{b}{2a}[/latex] |
| Plug-in the values for a and b | [latex]\displaystyle x= -\frac{4}{2(1)}[/latex] |
| Solution of vertex and axis of symmetry | [latex]\displaystyle x= -2[/latex] |
| Graph the line |  |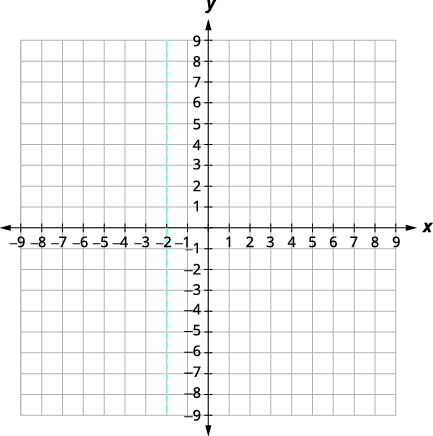
| Find f(x) when x = −2. | [latex]\displaystyle f(x) = x^2 + 4x + 5[/latex] |
| Plug-in x = −2, as indicated in red. | [latex]\displaystyle f(-2) = {\color{myred1}(-2)}^2 + 4.{\color{myred1}(-2)} + 5[/latex] |
| Simplify | [latex]\begin{align*} f(-2) &= 4 - 8 + 5 \\ f(-2) &= 1 \end{align*}[/latex] |
| Solution | The vertex is (−2, 1). |
| Graph the Vertex. |  |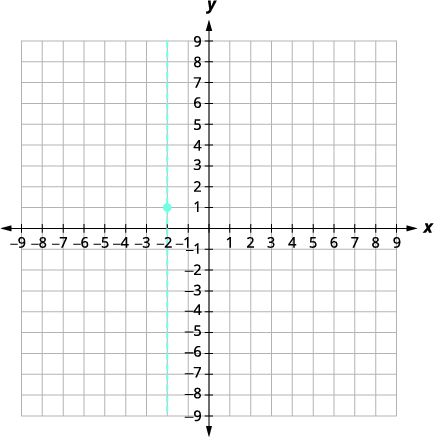
| The y-intercept occurs when x = 0. Find f(0). | [latex]\displaystyle f(x) = x^2 + 4x + 5[/latex] |
| Substitute x = 0. | [latex]\displaystyle f(0) = 5[/latex] |
| Solution | The y-intercept is (0, 5). |
| The point (−4, 5) is two units to the left of the line of symmetry.
The point two units to the right of the line of symmetry is (0, 5), point symmetric to the y-intercept |
 |
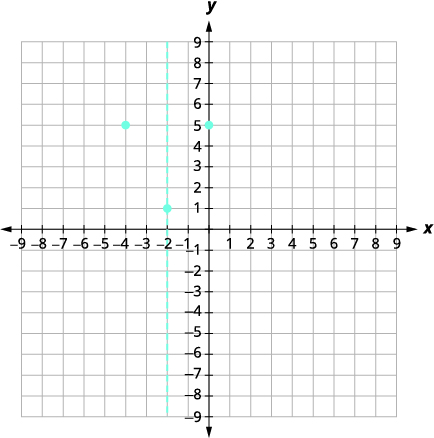| The x-intercept occurs when f(x) = 0. Find f(x) = 0, as indicated in red. | [latex]\displaystyle {\color{myred1}0} = x^2 + 4x + 5[/latex] |
| Test the discriminant. | [latex]\displaystyle D = b^2 - 4ac[/latex] |
| Simplify | [latex]\begin{align*} D &= 4^2 - 4 . 1 . 5 \\ D &= 16 - 20 \\ D &= -4\end{align*}[/latex] |
| X-intercept? | Since the value of the discriminant is negative, there is no real solution and so no x-intercept. |
| Connect the points to graph the parabola. You may want to choose two more points for greater accuracy. |  |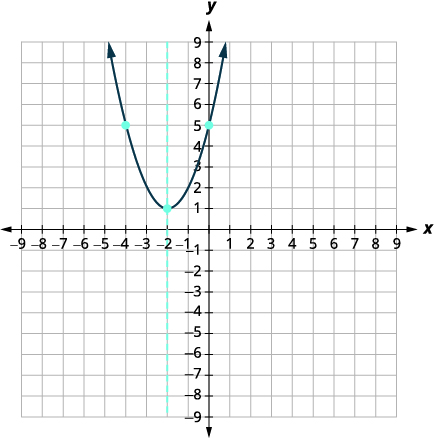
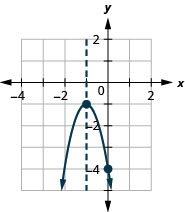
Graph f(x) = −3x2 − 6x − 4 by using its properties.
Solution (click to reveal)
Finding the y-intercept by finding f(0) is easy, isn’t it? Sometimes we need to use the Quadratic Formula to find the x-intercepts.
Graph f(x) = 2x2 − 4x − 3 by using its properties.
Solution (click to reveal)
| Steps | Algebraic |
| Function | [latex]\begin{align*} f(x) &= {\color{myred1}ax^2 + bx + c }\\ f(x) &= 2x^2 - 4x - 3 \end{align*}[/latex] |
| Since a = 2, the parabola opens upward. |  |
| To find the equation of the axis of symmetry, use [latex]\displaystyle x = -\frac{b}{2a}[/latex] | [latex]\displaystyle x= -\frac{b}{2a}[/latex] |
| Plug-in the values and Simplify | [latex]\displaystyle x= -\frac{-4}{2 . 2}[/latex] |
| The equation of the axis of symmetry is x = 1. | [latex]\displaystyle x= 1[/latex] |
| Original Function: The vertex is on the line x = 1. | [latex]\displaystyle f(x) = 2x^2 - 4x - 3[/latex] |
| Find f(1), as indicated in red. | [latex]\displaystyle f(1) = 2({\color{myred1}1})^2 - 4.{\color{myred1}1} - 3[/latex] |
| Simplify | [latex]\displaystyle f(1) = 2 - 4 - 3[/latex] |
| The vertex is (1, −5). | [latex]\displaystyle f(1) = -5[/latex] |
| Original Function: The y-intercept occurs when x = 0. | [latex]\displaystyle f(x) = 2x^2 - 4x - 3[/latex] |
| Find f(0), as indicated in red. | [latex]\displaystyle {\color{myred1}0} = 2.{\color{myred1}0}^2 - 4.{\color{myred1}0} - 3[/latex] |
| Simplify. The y-intercept is (0, −3). | [latex]\displaystyle f(0) = - 3[/latex] |
| The point (0, −3) is one unit to the left of the line of symmetry. The point one unit to the right of the line of symmetry is (2, −3). | Point symmetric to the y-intercept is (2, −3). |
| The x-intercept occurs when y = 0. | [latex]\displaystyle f(x) = 2x^2 - 4x - 3[/latex] |
| Find f(x) = 0, as indicated in red. | [latex]\displaystyle {\color{myred1}0} = 2x^2 - 4x - 3[/latex] |
| Use the Quadratic Formula. | [latex]\displaystyle x= \frac{-b\pm\sqrt{b^2−-4ac}}{2a}[/latex] |
| Substitute in the values of a, b and c. | [latex]\displaystyle x= \frac{-(-4)\pm\sqrt{(-4)^2−-4(2)(3)}}{2(2)}[/latex] |
| Simplify. | [latex]\displaystyle x= \frac{4\pm\sqrt{16 + 24}}{4}[/latex] |
| Simplify inside the radical. | [latex]\displaystyle x= \frac{4\pm\sqrt{40}}{4}[/latex] |
| Simplify the radical. | [latex]\displaystyle x= \frac{4\pm 2\sqrt{10}}{4}[/latex] |
| Factor the GCF. | [latex]\displaystyle x= \frac{2(2\pm\sqrt{10})}{4}[/latex] |
| Remove common factors. | [latex]\displaystyle x= \frac{2\pm\sqrt{10}}{2}[/latex] |
| Write as two equations. | [latex]\begin{align*} x &= \frac{2 + \sqrt{10}}{2} \\ x &= \frac{2 - \sqrt{10}}{2} \end{align*}[/latex] |
| Approximate the values. | [latex]\begin{align*} x &\approx 2.5 \\ x &\approx -0.6 \end{align*}[/latex] |
| Solution | The approximate values of the x-intercepts are (2.5, 0) and (−0.6, 0). |
| Graph the parabola using the points found. |  |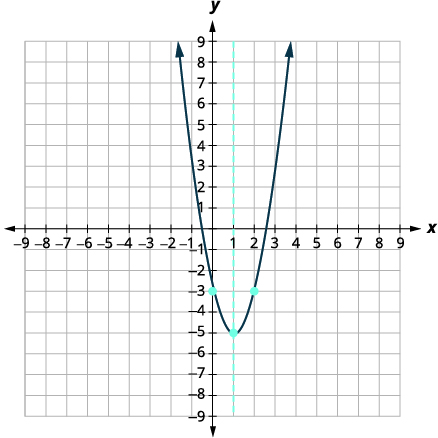
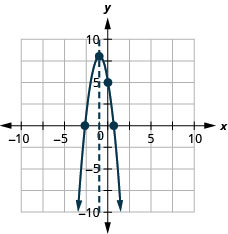
Graph f(x) = −3x2 − 6x + 5 by using its properties.
Solution (click to reveal)
Solve Maximum and Minimum Applications
Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function. The y-coordinate of the vertex is the minimum value of a parabola that opens upward. It is the maximum value of a parabola that opens downward. See the graphs below.
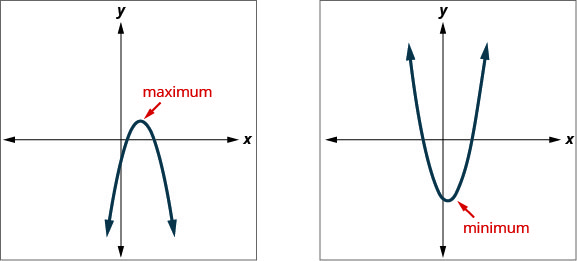
Minimum or Maximum Values of a Quadratic Function
The y-coordinate of the vertex of the graph of a quadratic function is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
So
[latex]\displaystyle f\left(\frac{-b}{2a}\right) [/latex]
is the Minimum or Maximum depending on the parabola's orientation.
Try it!
Find the minimum or maximum value of the quadratic function
f(x) = x2 + 2x − 8.
Solution (click to reveal)
| Steps | Algebraic |
| Function | [latex]\displaystyle f(x) = x^2 + 2x - 8[/latex] |
| Since a is positive, the parabola opens upward. |
The quadratic equation has a minimum. |
| Find the equation of the axis of symmetry. | [latex]\displaystyle x= -\frac{b}{2a}[/latex] |
| Plug-in the values | [latex]\displaystyle x= -\frac{2}{2 . 1}[/latex] |
| Solution: The equation of the axis of symmetry is x = −1. | [latex]\displaystyle x= -1[/latex] |
| The vertex is on the line x=−1. | [latex]\displaystyle f(x) = x^2 + 2x - 8[/latex] |
| Find f(−1), as indicated in red. | [latex]\displaystyle f(-1) = {\color{myred1}(-1)}^2 + 2{\color{myred1}(-1)} - 8[/latex] |
| Simplify | [latex]\displaystyle f(-1) = 1 - 2 - 8[/latex] |
| Solution: The vertex is (−1, −9). | [latex]\displaystyle f(-1) = - 9[/latex] |
| Since the parabola has a minimum, the y-coordinate of the vertex is the minimum y-value of the quadratic equation. |
The minimum value of the quadratic is −9 and it occurs when x = −1. |
| Show the graph to verify the result. |  |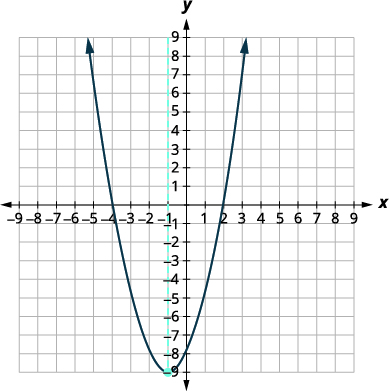
Find the maximum or minimum value of the quadratic function
f(x) = x2 − 8x + 12.
Solution (click to reveal)
The minimum value of the quadratic function is −4 and it occurs when x = 4.
Find the maximum or minimum value of the quadratic function
f(x) = −4x2 + 16x − 11.
Solution (click to reveal)
The maximum value of the quadratic function is 5 and it occurs when x = 2.
Access these online resources for additional instruction and practice with graphing quadratic functions using properties.
Key Concepts
- Parabola Orientation
- For the graph of the quadratic function f(x) = ax2 + bx +c, if
- a > 0, the parabola opens upward.
- a < 0, the parabola opens downward.
- For the graph of the quadratic function f(x) = ax2 + bx +c, if
- Axis of Symmetry and Vertex of a Parabola: The graph of the function f(x) = ax2 + bx +c is a parabola where:
- the axis of symmetry is the vertical line [latex]\displaystyle x = -\frac{b}{2a}[/latex].
- the vertex is a point on the axis of symmetry, so its x-coordinate is [latex]\displaystyle -\frac{b}{2a}[/latex].
- the y-coordinate of the vertex is found by substituting [latex]\displaystyle x = -\frac{b}{2a}[/latex] into the quadratic equation.
- Find the Intercepts of a Parabola
- To find the intercepts of a parabola whose function is f(x) = ax2 + bx + c:
y-intercept x-intercepts Let x = 0 and solve for f(x) Let f(x) = 0 and solve for x
- To find the intercepts of a parabola whose function is f(x) = ax2 + bx + c:
- How to graph a quadratic function using properties.
- Determine whether the parabola opens upward or downward.
- Find the equation of the axis of symmetry.
- Find the vertex.
- Find the y-intercept. Find the point symmetric to the y-intercept across the axis of symmetry.
- Find the x-intercepts. Find additional points if needed.
- Graph the parabola.
- Minimum or Maximum Values of a Quadratic Equation
- The y-coordinate of the vertex of the graph of a quadratic equation is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
