25 Dividing Polynomials
Topics Covered
Polynomial Division Review
The method we’ll use to divide a polynomial by a monomial is based on the properties of fraction addition. So we’ll start with an example to review fraction addition. The sum ![]() simplifies to
simplifies to ![]() .
.
Now we will do this in reverse to split a single fraction into separate fractions. For example, ![]() can be written
can be written ![]() .
.
This is the “reverse” of fraction addition and it states that if a, b, and c are numbers where c ≠ 0, then ![]() . We will use this to divide polynomials by monomials.
. We will use this to divide polynomials by monomials.
Division of a Polynomial by a Monomial
To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
Try it!
1. Find the quotient: (18x3y − 36xy2) ÷ (-3xy).
| Steps | Algebraic |
| Rewrite as a fraction. | |
| Divide each term by the divisor. Be careful with the signs! | |
| Simplify. |
2. Find the quotient: (32a2b – 16ab2) ÷ (-8ab).
Solution:
-4a + 2b
3. Find the quotient: (-48a8b4 – 36a6b5) ÷ (-6a3b3).
Solution:
8a5b + 6a3b2
Divide Polynomials Using Long Division
To divide a polynomial by a binomial, we follow a procedure very similar to long division of numbers. We start by dividing into the digits of the dividend that have the greatest place value. We divide, multiply, subtract, include the digit in the next place value position, and repeat. So let’s look carefully the steps we take when we divide a 3-digit number, 875, by a 2-digit number, 25. 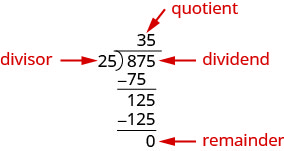 We check division by multiplying the quotient by the divisor.
We check division by multiplying the quotient by the divisor.
If we did the division correctly, the product of quotient and divisor should equal the dividend.
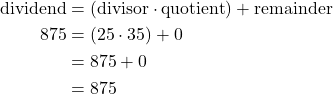
This process demonstrates the division algorithm.
Division Algorithm
The Division Algorithm states that, given a polynomial dividend f(x) and a non-zero polynomial divisor d(x) where the degree of d(x) is less than or equal to the degree of f(x), there exist unique polynomials q(x) and r(x) such that
f(x) = d(x)q(x) + r(x)
q(x) is the quotient and r(x) is the remainder. The remainder is either equal to zero or has degree strictly less than d(x).
If r(x) = 0, then d(x) divides evenly into f(x). This means that, in this case, both d(x) and q(x) are factors of f(x).
Now we will divide a trinomial by a binomial. As you read through the example, notice how similar the steps are to the numerical example above.
Try it!
1. Find the quotient: (x2 + 9x + 20) ÷ (x + 5).
Solution :
| Steps | Algebraic |
| Write it as a long division problem.
Be sure the dividend is in standard form. |
|
| Divide x2 by x. It may help to ask yourself, “What do I need to multiply x by to get x2?” | |
| Put the answer, x, in the quotient over the x term.
Multiply x times x + 5. Line up the like terms under the dividend. |
|
| Subtract x2 + 5x from x2 + 9x.
You may find it easier to change the signs and then add. Then bring down the last term, 20. |
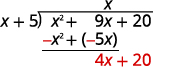 |
| Divide 4x by x. It may help to ask yourself, “What do I need to multiply x by to get 4x?”
Put the answer, 4, in the quotient over the constant term. |
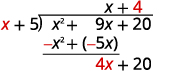 |
| Multiply 4 times x + 5. | 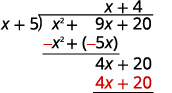 |
| Subtract 4x + 20 from 4x + 20. | 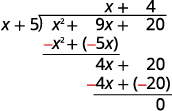 |
| Check:
Multiply the quotient by the divisor. You should get the dividend. |
(x + 4)(x + 5) x2 + 9x + 20 ✓ |
2. Find the quotient: (y2 + 10y + 21) ÷ (y + 3).
Solution:
y + 7
When we divided 875 by 25, we had no remainder. But sometimes, division of numbers does leave a remainder. The same is true when we divide polynomials. In the next example, we’ll have a division that leaves a remainder. We write the remainder as a fraction with the divisor as the denominator.
Look back at the dividends in previous examples. The terms were written in descending order of degrees, and there were no missing degrees. The dividend in this example will be x4 – x2 + 5x – 6. It is missing an x3 term. We will add in 0x3 as a placeholder.
Given a polynomial and a binomial, use long division to divide the polynomial by the binomial.
- Arrange the terms in descending order of degrees for both the dividend and divisor. Remember to add in any missing degrees as a placeholder for the dividend
- Set up the division problem.
- Determine the first term of the quotient by dividing the leading term of the dividend by the leading term of the divisor.
- Multiply the answer by the divisor and write it below the like terms of the dividend.
- Subtract the bottom binomial from the top binomial.
- Bring down the next term of the dividend.
- Repeat steps 2-5 until reaching the last term of the dividend.
- If the remainder is non-zero, express as a fraction using the divisor as the denominator.
Try it!
1. Find the quotient: (x4 − x2 + 5x − 6) ÷ (x + 2).
Solution:
Notice that there is no x3 term in the dividend. We will add 0x3 as a placeholder.
| Steps | Algebraic |
|
|
|
| Write it as a long division problem.
Be sure the dividend is in standard form with placeholders for missing terms. |
|
| Divide x4 by x. Put the answer, x3, in the quotient over the x3 term.
Multiply x3 times x + 2. Line up the like terms. Subtract and then bring down the next term. |
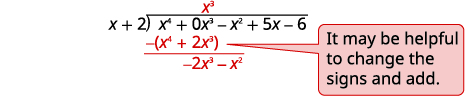 |
| Divide -2x3 by x. Put the answer, 2x2, in the quotient over the x2 term.
Multiply –2x2 times x + 1. Line up the like terms. Subtract and bring down the next term. |
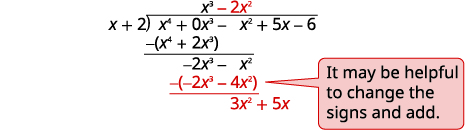 |
| Divide 3x2 by x. Put the answer, 3x, in the quotient over the x term.
Multiply 3x times x + 1. Line up the like terms. Subtract and bring down the next term. |
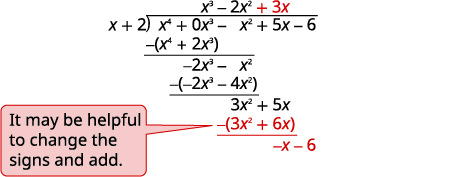 |
| Divide -x by x. Put the answer, -1, in the quotient over the constant term.
Multiply -1 times x + 1. Line up the like terms. Change the signs, add. Write the remainder as a fraction with the divisor as the denominator. |
 |
| To check, multiply
The result should be |
2. Find the quotient: (x4 − 7x2 + 7x + 6) ÷ (x + 3).
Solution:
![]()
In the next example, we will divide by 2a + 3. As we divide, we will have to consider the constants as well as the variables.
Try it!
1. Find the quotient: (8a3 + 27) ÷ (2a + 3).
Solution:
This time we will show the division all in one step. We need to add two placeholders in order to divide.
| Solution |
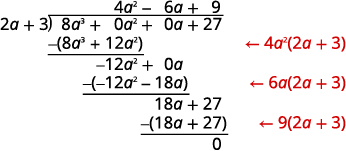 |
To check, multiply (2a + 3)(4a2 − 6a + 9).
The result should be 8a3 + 27.
2. Find the quotient: (125x3 − 8) ÷ (5x − 2).
Solution:
25x2 + 10x + 4
In the following example, we use division algorithm form to write the solution. Notice the answer is not just the quotient.
Try it! – Using Long Division to Divide a Second-Degree Polynomial
Divide 5x2 + 3x − 2 by x + 1.
Solution:

The quotient is 5x − 2.
The remainder is 0. We write the result as
![]()
or
![]()
Analysis:
This division problem had a remainder of 0. This tells us that the dividend is divided evenly by the divisor and that the divisor is a factor of the dividend.
Divide Polynomials using Synthetic Division
As we have mentioned before, mathematicians like to find patterns to make their work easier. Since long division can be tedious, let’s look back at the long division we did in a previous example and look for some patterns. We will use this as a basis for what is called synthetic division. The same problem in the synthetic division format is shown next.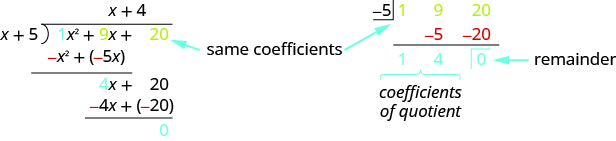 Synthetic division basically just removes unnecessary repeated variables and numbers. Here all the x and x2 are removed as well as the -x2 and −4x as they are opposite the term above.
Synthetic division basically just removes unnecessary repeated variables and numbers. Here all the x and x2 are removed as well as the -x2 and −4x as they are opposite the term above.
The first row of the synthetic division is the coefficients of the dividend. The −5 is the opposite of the 5 in the divisor.
The second row of the synthetic division are the numbers shown in red in the division problem.
The third row of the synthetic division are the numbers shown in blue in the division problem.
Notice the quotient and remainder are shown in the third row.
Synthetic division only works when the divisor is of the form x − c.
Synthetic Division
Synthetic division is a shortcut that can be used when the divisor is a binomial in the form x − c where c is a real number.
In synthetic division, only the coefficients are used in the division process.
The following example will explain the process. Notice that the divisor is x + 2. In this case, it is not a minus sign, but a plus. All you do is write the x + 2 as x – (-2). Making c = -2.
Try it!
Use synthetic division to find the quotient and remainder when 2x3 + 3x2 + x + 8 is divided by x + 2.
Solution:
| Steps | Algebraic |
| Write the dividend with decreasing powers of x. | |
| Write the coefficients of the terms as the first row of the synthetic division. | |
| Write the divisor as x − c and place c in the synthetic division in the divisor box. | |
| Bring down the first coefficient to the third row. |  |
| Multiply that coefficient by the divisor and place the result in the second row under the second coefficient. | 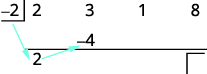 |
| Add the second column, putting the result in the third row. | 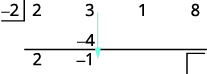 |
| Multiply that result by the divisor and place the result in the second row under the third coefficient. | 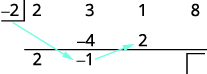 |
| Add the third column, putting the result in the third row. | 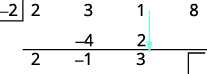 |
| Multiply that result by the divisor and place the result in the third row under the third coefficient. | 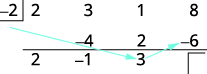 |
| Add the final column, putting the result in the third row. | 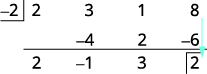 |
| The quotient is 2x2 − 1x + 3 and the remainder is 2. |
The division is complete. The numbers in the third row give us the result. The 2 −1 3 are the coefficients of the quotient. The quotient is 2x2 − 1x + 3. The 2 in the box in the third row is the remainder.
Check:
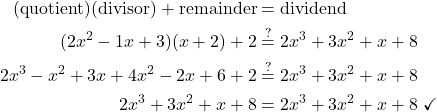
How To Divide a Polynomial by x − c
- Arrange the terms of in descending order of degrees, for both the dividend and divisor, adding a 0 coefficient for any missing degrees.
- Write c for the divisor.
- Write the coefficients of the dividend to the right.
- Bring the lead coefficient down to the bottom row.
- Multiply the lead coefficient by c. Write the product in the next column on the second row.
- Add the terms of the second column and write the sum on the bottom row.
- Repeat the Multiplication/Addition steps until all columns are filled. Multiply the result by c. Write the product in the next column.
- Repeat steps 5 and 6 for the remaining columns.
- Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree 0, the next number from the right has degree 1, the next number from the right has degree 2, and so on. You may need to write the remainder over the divisor rather than just state the remainder separately.
Try it!
Use synthetic division to find the quotient and remainder when 3x3 + 10x2 + 6x – 2 is divided by x + 2.
Solution:
3x2 + 4x – 2; 2
In the next example, we will do all the steps together.
Try it!
1. Use synthetic division to find the quotient and remainder when x4 – 16x2 + 3x + 12x is divided by x + 4.
Solution:
The polynomial x4 – 16x2 + 3x + 12 has its term in order with descending degree but we notice there is no x3 term. We will add a 0 as a placeholder for the x3 term. In x – c form, the divisor is x – (-4).
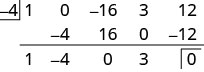 We divided a 4th degree polynomial by a 1st degree polynomial so the quotient will be a 3rd degree polynomial.
We divided a 4th degree polynomial by a 1st degree polynomial so the quotient will be a 3rd degree polynomial.
Reading from the third row, the quotient has the coefficients 1 -4 0 3, which is x3 – 4x2 + 3. The remainder is 0.
2. Use synthetic division to find the quotient and remainder when x4 – 16x2 + 5x + 20 is divided by x + 4.
Solution:
x3 – 4x2 + 5; 0
Solution:
Notice there is no x-term. We will use a zero as the coefficient for that term.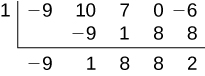 The result is
The result is ![]() .
.
Solution:
![]() .
.
Use the Remainder and Factor Theorem
Let’s look at the division problems we have just worked that ended up with a remainder. They are summarized in the chart below. If we take the dividend from each division problem and use it to define a function, we get the functions shown in the chart. When the divisor is written as x – c, the value of the function at c, f(c), is the same as the remainder from the division problem.
| Dividend | Divisor x – c | Remainder | Function | f(c) |
|---|---|---|---|---|
| x4 – x2 + 5x – 6 | x – (-2) | -4 | f(x) = x4 – x2 + 5x – 6 | -4 |
| 3x3 – 2x2 – 10x + 8 | x – 2 | 4 | f(x) = 3x3 – 2x2 – 10x + 8 | 4 |
| x4 – 16x2 + 3x + 15 | x – (-4) | 3 | f(x) = x4 – 16x2 + 3x + 15 | 3 |
To see this more generally, we realize we can check a division problem by multiplying the quotient by the divisor and adding the remainder. This should look familiar as it uses the Division Algorithm we showed you earlier, f(x) = d(x)q(x) + r(x). In function notation, we could say to get the dividend f(x), we multiply the quotient, q(x) times the divisor, x – c, and add the remainder, r.
| Steps | Algebraic |
| If we evaluate this at c, we get: | |
This leads us to the Remainder Theorem.
Remainder Theorem
If the polynomial function f(x) is divided by x − c, then the remainder is f(c).
Try it!
1. Use the Remainder Theorem to find the remainder when f(x) = x3 + 3x + 19 is divided by x + 2.
Solution:
To use the Remainder Theorem, we must use the divisor in the x – c form. We can write the divisor x + 2 as x – ( -2).
So, our c is -2.
To find the remainder, we evaluate f(c) which is f(−2).
| Steps | Algebraic |
| To evaluate f(-2), substitute x = -2. | |
| Simplify. | |
| The remainder is 5 when |
|
| Check: Use synthetic division to check. |
|
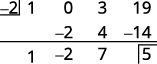 |
|
| The remainder is 5. |
2. Use the Remainder Theorem to find the remainder when f(x) = x3 – 7x + 12 is divided by x + 3.
Solution:
6
In the next example, we evaluate the function by using synthetic division first.
Try it! – Using the Remainder Theorem to Evaluate a Polynomial
Use the Remainder Theorem to evaluate f(x) = 6x4 – x3 – 15x2 + 2x – 7 at x = 2.
Solution:
To find the remainder using the Remainder Theorem, use synthetic division to divide the polynomial by x – 2.
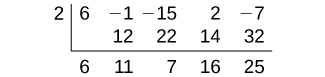 The remainder is 25. Therefore, f(2) = 25.
The remainder is 25. Therefore, f(2) = 25.
Analysis:
We can check our answer by evaluating f(2).
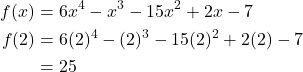
Factor Theorem
The Factor Theorem is another theorem that helps us analyze polynomial equations. It tells us how the zeros of a polynomial are related to the factors. Recall the Division Algorithm, f(x) = (x – c)q(x) + r.
When we divided 8a3 + 27 by 2a + 3 as seen in a previous example, the result was 4a2 – 6a + 9. To check our work, we multiply 4a2 – 6a + 9 by 2a + 3 to get 8a3 + 27.
(4a2 – 6a + 9)(2a + 3) = 8a3 + 27
Written this way, we can see that 4a2 – 6a + 9 and 2a + 3 are factors of 8a3 + 27. When we did the division, the remainder was zero.
Whenever a divisor, x – c, divides a polynomial function, f(x), and resulting in a remainder of zero, we say x – c is a factor of f(x).
The reverse is also true. If x – c is a factor of f(x) then x – c will divide the polynomial function resulting in a remainder of zero.
We will state this in the Factor Theorem.
Factor Theorem
For any polynomial function f(x),
- if x – c is a factor of f(x), then f(c) = 0.
- if f(c) = 0, then x – c is a factor of f(x).
Try it!
1. Use the Remainder Theorem to determine if x – 4 is a factor of f(x) = x3 – 64.
Solution:
The Factor Theorem tells us that x – 4 is a factor of f(x) = x3 – 64 if f(4) = 0.
| Steps | Algebraic |
| f(x) = x3 – 64 | |
| To evaluate f(4) substitute x = 4 | f(4) = (4)3 – 64 |
| Simplify | f(4) = 64 – 64 |
| Subtract | f(4) = 0 |
Since f(4) = 0, x – 4 is a factor of f(x) = x3 – 64.
2. . Use the Remainder Theorem to determine if x – 5 is a factor of f(x) = x3 – 125.
Solution:
yes
Try it! – Using the Factor Theorem to Find the Zeros of a Polynomial Expression
Solution:
We can use synthetic division to show that (x + 2) is a factor of the polynomial.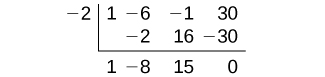 The remainder is zero, so (x + 2) is a factor of the polynomial. We can use the Division Algorithm to write the polynomial as the product of the divisor and the quotient:
The remainder is zero, so (x + 2) is a factor of the polynomial. We can use the Division Algorithm to write the polynomial as the product of the divisor and the quotient:
(x + 2)(x2 – 8x + 15)
We can factor the quadratic factor to write the polynomial as
(x + 2)(x – 3)(x – 5)
By the Factor Theorem, the zeros of x3 – 6x2 – x + 30 are -2, 3, and 5.
2. Use the Factor Theorem to find the zeros of f(x) = x3 + 4x2 – 4x – 16 given that (x – 2) is a factor of the polynomial.
Solution:
The zeros are 2, -2, and -4.
Access these online resources for additional instruction and practice with dividing polynomials.
- Dividing a Polynomial by a Binomial
- Synthetic Division & Remainder Theorem
- Dividing a Trinomial by a Binomial Using Long Division
- Dividing a Polynomial by a Binomial Using Long Division
- Ex 2: Dividing a Polynomial by a Binomial Using Synthetic Division
- Ex 4: Dividing a Polynomial by a Binomial Using Synthetic Division
Key Concepts
- Division of a Polynomial by a Monomial
- To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
- Polynomial long division can be used to divide a polynomial by any polynomial with equal or lower degree.
- The Division Algorithm tells us that a polynomial dividend can be written as the product of the divisor and the quotient added to the remainder.
- Synthetic division is a shortcut that can be used to divide a polynomial by a binomial in the form x – k.
- Remainder Theorem
- If the polynomial function f(x) is divided by x – c, then the remainder is f(c).
- Factor Theorem: For any polynomial function f(x),
- if x – c is a factor of f(x), then f(c) = 0.
- if f(c) = 0, then x – c is a factor of f(x).
given a polynomial dividend f(x) and a non-zero polynomial divisor d(x) where the degree of d(x) is less than or equal to the degree of f(x), there exist unique polynomials q(x) and r(x) such that f(x) = d(x)q(x) + r(x) where q(x) is the quotient and r(x) is the remainder. The remainder is either equal to zero or has degree strictly less than d(x).
a shortcut method that can be used to divide a polynomial by a binomial of the form x - k
if a polynomial f(x) is divided by x - k, then the remainder is equal to the value f(k)
c is a zero of polynomial function f(x) if and only if (x - c) is a factor of f(x)

