15 Composite Functions and Domain
Topics Covered
By the end of this section, you will be able to:
- Find and evaluate composite functions
- Combine functions using algebraic operations.
- Create a new function by composition of functions.
- Evaluate composite functions.
- Find the domain of a composite function.
- Decompose a composite function into its component functions.
Domain Review
Lets first recap what we learned about domain from the Functions chapter.
- The smallest number from the interval is written first.
- The largest number in the interval is written second, following a comma.
- Parentheses, ( or ), are used to signify that an endpoint value is not included, called exclusive. They represent solutions greater or less than the number.
- Brackets, [ or ], are used to indicate that an endpoint value is included, called inclusive. They also represent solutions that are greater than or equal to or less than or equal to the number
| Set Indicated | Set-Builder Notation | Interval Notation |
|---|---|---|
| All real numbers between a and b, but not including a or b | {x|a < x < b} | (a, b) |
| All real numbers greater than a, but not including a | {x|x > a} | (a, ∞) |
| All real numbers less than b, but not including b | {x|x < b} | (−∞, b) |
| All real numbers greater than a, including a | {x|x ≥ a} | [a, ∞) |
| All real numbers less than b, including b | {x|x ≤ b} | (−∞, b] |
| All real numbers between a and b, including a | {x|a ≤ x < b} | [a, b) |
| All real numbers between a and b, including b | {x|a < x ≤ b} | (a, b] |
| All real numbers between a and b, including a and b | {x|a ≤ x ≤ b} | [a, b] |
| All real numbers less than a or greater than b | {x|x < a or x > b} | (−∞, a) ∪ (b, ∞) |
| All real numbers | {x|x is a real number} | (−∞, ∞) |
This format set-builder notation: {x|10 ≤ x < 30} describes the behavior of x in set-builder notation. The braces { } are read as “the set of,” and the vertical bar | is read as “such that,” so we would read {x | 10 ≤ x < 30} as “the set of x-values such that 10 is less than or equal to x, and x is less than 30.”
Previously we looked at finding domain of basic functions. But what about those cases where you have a function that is in the form of a fraction or has a square root?
Given a function written in an equation form that includes a fraction, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for x. If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Try it! – Finding the Domain of a Function Involving a Denominator
Find the domain of the function f(x) = ![]()
Solution:
When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for x.
Now, we will exclude 2 from the domain. The answers are all real numbers where x<2 or x>2 as shown below. We can use a symbol known as the union,∪, to combine the two sets. In interval notation, we write the solution: (−∞, 2) ∪ (2, ∞).
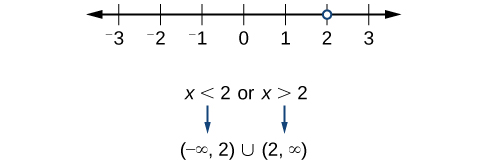
Given a function written in equation form including an even root, find the domain.
- Identify the input values.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for x.
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
Try it! – Finding the Domain of a Function with an Even Root
Find the domain of the function f(x)= ![]()
Solution:
When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand.
Set the radicand greater than or equal to zero and solve for x.
Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to 7, or (−∞,7].
2. Find the domain of the function ![]()
Solution:
[−![]() ,∞)
,∞)
Combining Functions Using Algebraic Operations
Function composition is only one way to combine existing functions. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. We do this by performing the operations with the function outputs, defining the result as the output of our new function.
Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We want to do this for every year, adding only that year’s incomes and then collecting all the data in a new column. If w(y) is the wife’s income and h(y) is the husband’s income in year y, and we want T to represent the total income, then we can define a new function.
If this holds true for every year, then we can focus on the relation between the functions without reference to a year and write
Just as for this sum of two functions, we can define difference, product, and ratio functions for any pair of functions that have the same kinds of inputs (not necessarily numbers) and also the same kinds of outputs (which do have to be numbers so that the usual operations of algebra can apply to them, and which also must have the same units or no units when we add and subtract). In this way, we can think of adding, subtracting, multiplying, and dividing functions.
For two functions f(x) and g(x) with real number outputs, we define new functions f + g, f − g, f g, and ![]() by the relations
by the relations
| Types | Algebraic | |
| Sum | (f + g)(x) = f(x) + g(x) | |
| Difference | (f – g) (x) = f(x) – g(x) | |
| Product | (f g)(x) = f(x)g(x) | |
| Quotient | ||
Try it! – Performing Algebraic Operations on Functions
Find and simplify the functions (g − f)(x) and ![]() , given f(x) = x − 1 and g(x) = x2 − 1. Are they the same function?
, given f(x) = x − 1 and g(x) = x2 − 1. Are they the same function?
Solution:
Begin by writing the general form, and then substitute the given functions.
(g − f )(x) = g(x) – f(x)
(g − f )(x) = x2 − 1 − (x − 1)
(g − f )(x) = x2 − x
(g − f )(x) = x(x – 1)
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() where x ≠ 1
where x ≠ 1
![]() = x + 1
= x + 1
No, the functions are not the same.
Note: For ![]() the condition x≠1 is necessary because when x=1, the denominator is equal to 0, which makes the function undefined.
the condition x≠1 is necessary because when x=1, the denominator is equal to 0, which makes the function undefined.
2. Find and simplify the functions (fg)(x) and (f − g)(x).
Are they the same function?
Solution:
(fg)(x) = f(x)g(x) = (x−1)(x2−1) = x3 − x2 − x + 1
(f−g)(x) = f(x)−g(x) = (x − 1)−(x2 − 1) = x − x2
No, the functions are not the same.
Find and Evaluate Composite Functions
Before we introduce the functions, we need to look at another operation on functions called composition. In composition, the output of one function is the input of a second function. For functions fand g, the composition is written f ∘ g and is defined by:
We read the left-hand side as “f composed with g at x,” and the right-hand side as “f of g of x.” The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol ∘ is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important not to confuse function composition with multiplication because, as we learned above, in most cases f(g(x)) ≠ f(x)g(x).
To do a composition, the output of the first function, g(x), becomes the input of the second function, f, and so we must be sure that it is part of the domain of f.
It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the equation above, the function g takes the input x first and yields an output g(x). Then the function f takes g(x) as an input and yields an output f(g(x)).
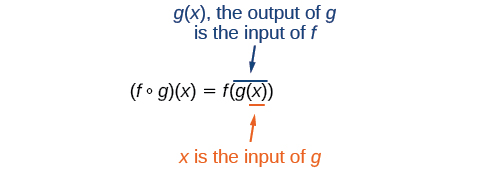
In general, f ∘ g and g∘ f are different functions. In other words, in many cases f(g(x)) ≠ g(f(x)) for all x. We will also see that sometimes two functions can be composed only in one specific order.
For example, if f(x) = x2 and g(x) = x + 2, then
but
These expressions are not equal for all values of x, so the two functions are not equal. It is irrelevant that the expressions happen to be equal for the single input value x = −![]() .
.
Note that the range of the inside function (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to make sense in terms of inputs and outputs.
Composition of Functions
When the output of one function is used as the input of another, we call the entire operation a composition of functions. For any input x and functions f and g, this action defines a composite function, which we write as f∘ g such that
The domain of the composite function f∘ g is all x such that x is in the domain of g and g(x) is in the domain of f.
It is important to realize that the product of functions fg is not the same as the function composition f(g(x)), because, in general, f(x)g(x) ≠ f(g(x)).
composite functionThe next example will demonstrate that (f∘ g)(x), (g∘ f)(x) and (f · g)(x) usually result in different outputs.
Try it!
For functions f(x)=4x − 5 and g(x)=2x + 3, find: a. (f∘ g)(x), b. (g∘ f)(x), and c. (f · g)(x).
Solution:
a.
|
Algebraic |
| Use the definition of (f∘ g)(x). | (f∘ g)(x) = f(g(x)) |
| Substitute 2x+3 for g(x) |
(f∘ g)(x) = f(2x+3) |
| Find f(2x+3) where f(x) = 4x -5 | (f∘ g)(x) = 4(2x+3) -5 |
| Distribute. | (f∘ g)(x) = 8x + 12 -5 |
| Simplify. | (f∘ g)(x) = 8x + 7 |
b.
| Steps | Algebraic |
| Use the definition of (g∘ f)(x). | (g∘ f)(x) = g(f(x)) |
| Substitute 4x-5 for f(x) | (g∘ f)(x) = g(4x-5) |
| Find g(4x -5) where g(x) = 2x+3 |
(g∘ f)(x) = 2(4x-5) +3 |
| Distribute. | (g∘ f)(x) = 8x-10+3 |
| Simplify. | (g∘ f)(x) = 8x -7 |
Notice the difference in the result in part a. and part b.
c. Notice that (f · g)(x) is different than (f∘ g)(x). In part a. we did the composition of the functions. Now in part c. we are not composing them, we are multiplying them.
| Steps | Algebraic |
| Use the definition of (f · g)(x). | (f · g)(x) = f(x) · g(x) |
| Substitute f(x) = 4x − 5 and g(x) = 2x + 3. | (f · g)(x) = (4x − 5) · (2x + 3) |
| Multiply. | (f · g)(x) = 8x2 + 2x − 15 |
2. For functions f(x)=3x − 2 and g(x)=5x + 1, find a. (f∘g)(x) b. (g∘f)(x) c. (f·g)(x).
Solution:
a. 15x + 1 b. 15x − 9 c. 15x2 − 7x − 2
In the next example we will evaluate a composition for a specific value.
Try it!
For functions f(x) = x2 − 4, and g(x) = 3x + 2, find: a. (f∘g)(−3), b. (g∘f)(−1).
Solution:
a.
| Steps | Algebraic |
| Use the definition of (f∘g)(−3). | (f∘g)(−3) = f(g(-3)) |
| Find g(-3) where g(x) = 3x + 2 | (f∘g)(−3) = f(3(-3) +2) |
| Simplify. | (f∘g)(−3) = f(-7) |
| Find f(-7) where f(x) = x2 − 4 | (f∘g)(−3) = (-7)2 – 4 |
| Simplify. | (f∘g)(−3) = 45 |
b.
| Steps | Algebraic |
| Use the definition of (g∘f)(−1). | (g∘ f)(x) = g(f(-1)) |
| Find f(-1) where f(x) = x2−4 | (g∘ f)(x) = g(-12−4) |
| Simplify. | (g∘ f)(x) = g(-3) |
| Find g(-7) where g(x) = 3x+2 | (g∘ f)(x) = 3(-3) + 2 |
| Simplify. | (g∘ f)(x) = -7 |
2. For functions f(x) = x2 − 9, and g(x) = 2x + 5, find a. (f∘ g)(−2), b. (g∘ f)(−3).
Solution:
a. –8 , b. 5
Finding the Domain of a Composite Function
As we discussed previously, the domain of a composite function such as f∘ g is dependent on the domain of g and the domain of f. It is important to know when we can apply a composite function and when we cannot, that is, to know the domain of a function such as f∘ g. Let us assume we know the domains of the functions f and g separately. If we write the composite function for an input x as f(g(x)), we can see right away that x must be a member of the domain of g in order for the expression to be meaningful, because otherwise we cannot complete the inner function evaluation. However, we also see that g(x) must be a member of the domain of f, otherwise the second function evaluation in f(g(x)) cannot be completed, and the expression is still undefined. Thus the domain of f∘ g consists of only those inputs in the domain of g that produce outputs from g belonging to the domain of f. Note that the domain of f composed with g is the set of all x such that x is in the domain of g and g(x) is in the domain of f.
Domain of a Composite Function
The domain of a composite function f(g(x)) is the set of those inputs x in the domain of g for which g(x) is in the domain of f.
Given a function composition f(g(x)), determine its domain.
- Find the domain of g.
- Find the domain of f.
- Find those inputs x in the domain of g for which g(x) is in the domain of f. That is, exclude those inputs x from the domain of g for which g(x) is not in the domain of f. The resulting set is the domain of f∘ g.
Try it! – Finding the Domain of a Composite Function
Find the domain of
The domain of g(x) consists of all real numbers except x = ![]() , since that input value would cause us to divide by 0. Likewise, the domain of f consists of all real numbers except 1. So we need to exclude from the domain of g(x) that value of x for which g(x) = 1.
, since that input value would cause us to divide by 0. Likewise, the domain of f consists of all real numbers except 1. So we need to exclude from the domain of g(x) that value of x for which g(x) = 1.
![]() = 1
= 1
4 = 3x – 2
6 = 3x
x = 2
So the domain of f∘ g is the set of all real numbers except ![]() and 2. This means that
and 2. This means that
We can write this in interval notation as
Try it! – Finding the Domain of a Composite Function Involving Radicals
Find the domain of
Because we cannot take the square root of a negative number, the domain of g is (−∞, 3].Now we check the domain of the composite function
For (f∘ g)(x) = ![]() ,
, ![]() ≥ 0, since the radicand of a square root must be positive. Since square roots are positive,
≥ 0, since the radicand of a square root must be positive. Since square roots are positive, ![]() ≥ 0, or,
≥ 0, or, ![]() ≥ 0, which gives a domain of (-∞, 3]
≥ 0, which gives a domain of (-∞, 3]
Analysis:
This example shows that knowledge of the range of functions (specifically the inner function) can also be helpful in finding the domain of a composite function. It also shows that the domain of f∘ g can contain values that are not in the domain of f, though they must be in the domain of g.
3. Find the domain of
[−4, 0) ∪ (0, ∞)
Decomposing a Composite Function into its Component Functions
In some cases, it is necessary to decompose a complicated function. In other words, we can write it as a composition of two simpler functions. There may be more than one way to decompose a composite function, so we may choose the decomposition that appears to be most expedient.
Decomposing a Function
Write f(x)= ![]() as the composition of two functions.
as the composition of two functions.
Solution:
We are looking for two functions, g and h,so f(x) = g(h(x)). To do this, we look for a function inside a function in the formula for f(x).As one possibility, we might notice that the expression 5-x2 is the inside of the square root. We could then decompose the function as
We can check our answer by recomposing the functions.
2. Write f(x) = ![]() as the composition of two functions.
as the composition of two functions.
Solution:
Possible answer:
g(x) = ![]()
h(x) = ![]()
f = h∘ g
Access these online resources for additional instruction and practice with composite functions.
Key Concepts
- The domain of a function includes all real input values that would not cause us to attempt an undefined mathematical operation, such as dividing by zero or taking the square root of a negative number.
- The domain of a function can be determined by listing the input values of a set of ordered pairs.
- The domain of a function can also be determined by identifying the input values of a function written as an equation.
- Interval values represented on a number line can be described using inequality notation, set-builder notation, and interval notation.
- For many functions, the domain and range can be determined from a graph.
- An understanding of toolkit functions can be used to find the domain and range of related functions.
- Composition of Functions: The composition of functions f and g, is written f∘ g and is defined by (f∘ g)(x) = f(g(x)). We read f(g(x)) as f of g of x.
- We can perform algebraic operations on functions.
- When functions are combined, the output of the first (inner) function becomes the input of the second (outer) function.
- The function produced by combining two functions is a composite function.
- The order of function composition must be considered when interpreting the meaning of composite functions.
- A composite function can be evaluated by evaluating the inner function using the given input value and then evaluating the outer function taking as its input the output of the inner function.
- The domain of a composite function consists of those inputs in the domain of the inner function that correspond to outputs of the inner function that are in the domain of the outer function.
- Just as functions can be combined to form a composite function, composite functions can be decomposed into simpler functions.
- Functions can often be decomposed in more than one way.
the new function formed by function composition, when the output of one function is used as the input of another

