More on Slope

Elizabeth Pople

7 More on Slope

Topics Covered:

By the end of this section, you will be able to:

Use slopes to identify parallel and perpendicular lines
Find an equation of a line parallel to a given line
Find an equation of a line perpendicular to a given line
Find average rate of change

In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:

Identify and Graph Parallel Lines
Identify and Graph Perpendicular Lines
Rates of Change
Key Concepts

Identify and Graph Parallel Lines

Two lines that have the same slope are called parallel lines. Parallel lines have the same steepness and never intersect.

We say this more formally in terms of the rectangular coordinate system. Two lines that have the same slope and different y-intercepts are called parallel lines.

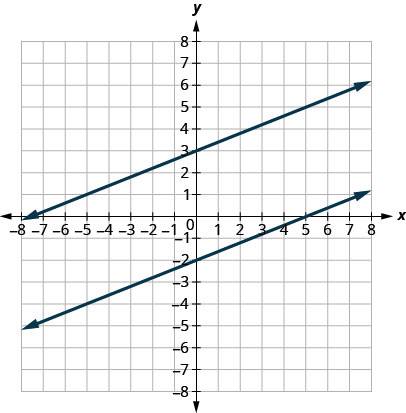
This figure shows the graph of a two straight lines on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The first line goes through the points (0, 3) and (5, 5). The second line goes through the points (0, negative 2) and (5, 0). The lines are parallel meaning they will always be the same distance apart and never intersect. They are slanted by the same angle.

Verify that both lines have the same slope, m = $\displaystyle\frac{2}{5}$ , and different y-intercepts.

What about vertical lines? The slope of a vertical line is undefined, so vertical lines don’t fit in the definition above. We say that vertical lines that have different x-intercepts are parallel, like the lines shown in this graph.

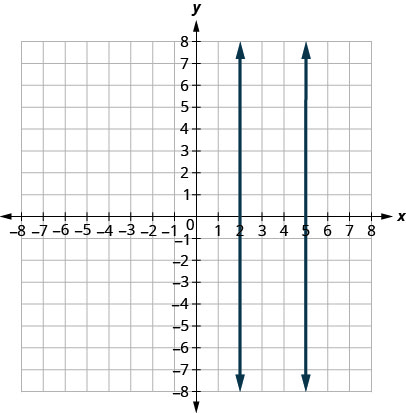
This figure shows the graph of a two straight vertical line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The first line goes through the points (2, 0) and (2, 1). The second line goes through the points (5, 0) and (5, 1). The lines are parallel meaning they will always be the same distance apart and never intersect.

Parallel lines

Parallel lines are lines in the same plane that do not intersect.

Parallel lines have the same slope and different y-intercepts.
If m₁ and m₂ are the slopes of two parallel lines then m₁ = m₂.
Parallel vertical lines have different x-intercepts.

Since parallel lines have the same slope and different y-intercepts, we can now just look at the slope–intercept form of the equations of lines and decide if the lines are parallel.

Try it!

Use slopes and y-intercepts to determine if the lines are parallel:

a. 3x − 2y = 6 and y = $\displaystyle\frac{3}{2}x$ + 1 b. y = 2x – 3 and −6x + 3y = −9.

Solution:

a.

Steps

Algebraic

3x -2y = 6

y = $\displaystyle\frac{3}{2}x$ + 1

Solve the first equation for y.

-2y = -3x + 6

$\displaystyle\frac{-2y}{-2}$ = $\displaystyle\frac{-3x + 6}{-2}$

The equation is now in slope–intercept form.

y = $\displaystyle\frac{3}{2}x$ – 3

The equation of the second line is already in slope-intercept form

y = $\displaystyle\frac{3}{2}x$ + 1

y = $\displaystyle\frac{3}{2}x$ – 3

y = $\displaystyle\frac{3}{2}x$ + 1

Identify the slope andy-intercept of both lines.

y = mx + b

m = $\displaystyle\frac{3}{2}$

y – Intercept is (0, -3)

y – Intercept is (0, 1)

The lines have the same slope and different y-intercepts and so they are parallel.
You may want to graph the lines to confirm whether they are parallel.

b.

Steps

Algebraic

y = 2x – 3

-6x + 3y = -9

The first equation is already in slope–intercept form.

y = 2x – 3

Solve the second equation for y.

3y = 6x – 9

$\displaystyle\frac{3y}{3}$ = $\displaystyle\frac{6x - 9}{3}$

The second equation is now in slope–intercept form.

y = 2x – 3

Identify the slope andy-intercept of both lines.

y = 2x – 3

y = mx + b

m = 2

y – Intercept is (0, -3)

y – Intercept is (0, 1)

The lines have the same slope, but they also have the same y-intercepts. Their equations represent the same line and we say the lines are coincident. They are not parallel; they are the same line.

Use slopes and y-intercepts to determine if the lines are parallel:

a. 2x + 5y = 5 and y = − $\displaystyle\frac{2}{5}x$ − 4 b. y = − $\displaystyle\frac{1}{2}x$ − 1 and x + 2y = −2.

Solution:

a. parallel b. not parallel; same line

Use slopes and y-intercepts to determine if the lines are parallel:

a. y = −4 and y = 3 b. x = −2 and x = −5.

Solution:

a. y = −4 and y = 3

We recognize right away from the equations that these are horizontal lines, and so we know their slopes are both 0. Since the horizontal lines cross the y-axis at y=−4 and at y=3, we know the y-intercepts are (0, −4) and (0, 3).

The lines have the same slope and different y-intercepts and so they are parallel.

b. x = −2 and x = −5
We recognize right away from the equations that these are vertical lines, and so we know their slopes are undefined. Since the vertical lines cross the x-axis at x=−2 and x=−5, we know the y-intercepts are (−2, 0) and (−5, 0).
The lines are vertical and have different x-intercepts and so they are parallel.

Use slopes and y-intercepts to determine if the lines are parallel:

a. y = 8 and y = −6 b. x = 1 and x = −5.

Solution:

a. parallel b. parallel

Find an Equation of a Line Parallel to a Given Line

Suppose we need to find an equation of a line that passes through a specific point and is parallel to a given line. We can use the fact that parallel lines have the same slope. So we will have a point and the slope—just what we need to use the point-slope equation.

First, let’s look at this graphically.

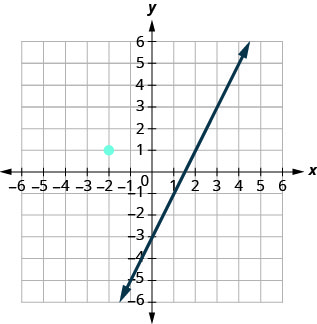
This graph shows y = 2x − 3. We want to graph a line parallel to this line and passing through the point (−2, 1).
This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 3, negative 6), (0, negative 4), (3, negative 2), and (6, 0). We know that parallel lines have the same slope. So the second line will have the same slope as y=2x−3. That slope is m_∥= 2. We’ll use the notation m_∥ to represent the slope of a line parallel to a line with slope m. (Notice that the subscript || looks like two parallel lines.)

The second line will pass through (−2, 1)and have m = 2.

To graph the line, we start at (−2, 1) and count out the rise and run. With m=2(or m= $\displaystyle\frac{2}{1}$ ), we count out the rise 2 and the run 1. We draw the line, as shown in the graph.

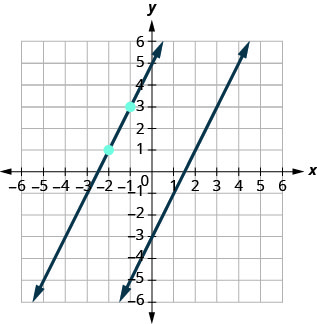
This figure has a graph of a two straight lines on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The first line goes through the points (0, negative 3), (1, negative 1), and (2, 1). The points (negative 2, 1) and (negative 1, 3) are plotted. The second line goes through the points (negative 2, 1) and (negative 1, 3)

Do the lines appear parallel? Does the second line pass through (−2, 1)?

We were asked to graph the line, now let’s see how to do this algebraically.

We can use either the slope-intercept form or the point-slope form to find an equation of a line. Here we know one point and can find the slope. So we will use the point-slope form.

Find an equation of a line parallel to a given line.

Find the slope of the given line.
Find the slope of the parallel line.
Identify the point.
Substitute the values into the point-slope form: y − y₁= m(x − x₁).
Write the equation in slope-intercept form.

Try it! – How to Find the Equation of a Line Parallel to a Given Line and a Point

Find an equation of a line parallel to y = 2x − 3 that contains the point (−2, 1). Write the equation in slope-intercept form.

Solution:

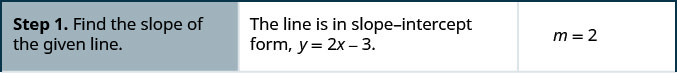
Step 1 is to find the slope of the given line. The line is in slope-intercept form, y equals 2 x minus 3. m equals 2.

Step 2 is to find the slope of the parallel line. Parallel lines have the same slope. m equals 2.

Step 4 is to substitute the values into the point-slope form y minus y 1 equals m times the quantity x minus x 1 in parentheses. y minus 1 equals 2 times the quantity x minus negative 2 in parentheses. This simplifies to y minus 1 equals 2 x plus 4.

Step 5 is to write the equation in slope-intercept form. y equals 2 x plus 5.

Look at graph with the parallel lines shown previously. Does this equation make sense? What is the y-intercept of the line? What is the slope?

Find an equation of a line parallel to the line y = 3x + 1 that contains the point (4, 2). Write the equation in slope-intercept form.

Solution:

y = 3x − 10

Find an equation of a line parallel to the line y = $\displaystyle\frac{1}{2}x$ − 3 that contains the point (6, 4). Write the equation in slope-intercept form.

Solution:

y= $\displaystyle\frac{1}{2}x$ + 1

Identify and Graph Perpendicular Lines

Let’s look at the lines whose equations are y = $\displaystyle\frac{1}{4}x$ − 1 and y = −4x + 2.

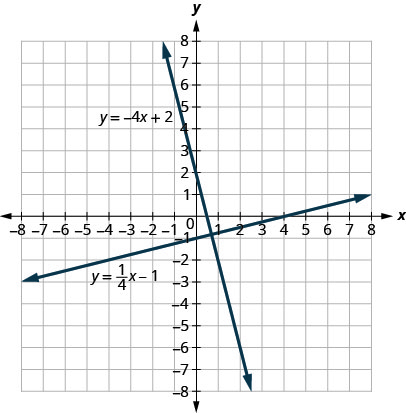
This figure shows the graph of a two perpendicular straight lines on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The first line goes through the points (0, negative 1) and (4, 0). The first line is labeled y equals 1 divided by 4 x minus 1. The second line goes through the points (0, 2) and (1, negative 2). The second line is labeled y equals negative 4 x plus 2. The lines are perpendicular meaning they form a right angle where they intersect.

These lines lie in the same plane and intersect in right angles. We call these lines perpendicular.

If we look at the slope of the first line, m₁ = $\displaystyle\frac{1}{4}$ , and the slope of the second line, m₂= −4, we can see that they are negative reciprocals of each other. If we multiply them, their product is −1.

m₁·m₂

$\displaystyle\frac{1}{4}(-4)$

-1

This is always true for perpendicular lines and leads us to this definition.

Perpendicular lines

Perpendicular lines are lines in the same plane that form a right angle.

If m₁ and m₂ are the slopes of two perpendicular lines, then:
- their slopes are negative reciprocals of each other, m₁= – $\displaystyle\frac{1}{m_2}$ .
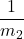- the product of their slopes is −1, m₁ · m₂ = −1.
A vertical line and a horizontal line are always perpendicular to each other.

We were able to look at the slope–intercept form of linear equations and determine whether or not the lines were parallel. We can do the same thing for perpendicular lines.

We find the slope–intercept form of the equation and then see if the slopes are opposite reciprocals. If the product of the slopes is −1, the lines are perpendicular.

Try it!

Use slopes to determine if the lines are perpendicular:

a. y = −5x − 4 and x − 5y = 5 b. 7x + 2y = 3 and 2x + 7y = 5

Solution:

a.

Steps

Algebraic

The first equation is in slope–intercept form.

y = − 5x − 4

Solve the second equation for y.

x − 5y = 5

−5y = − x + 5

$\displaystyle\frac{-5y}{-5}$ = $\displaystyle\frac{-x + 5}{-5}$

y = $\displaystyle\frac{1}{5}x$ – 1

Identify the slope of each line.

y = -5x – 4

y = mx + b

m₁ = -5

y = $\displaystyle\frac{1}{5}x$ – 1

y = mx + b

m1 = $\displaystyle\frac{1}{5}$

The slopes are negative reciprocals of each other, so the lines are perpendicular. We check by multiplying the slopes, Since $\displaystyle-5(\frac{1}{5})$ = −1, it checks.

b.

Steps

Algebraic

Solve the equations for y.

7x + 2y = 3

2y = -7x + 3

$\displaystyle\frac{2y}{2}$ = $\displaystyle\frac{-7x + 3}{2}$

2x + 7y = 5

7y = -2x + 5

$\displaystyle\frac{7y}{7}$ = $\displaystyle\frac{-2x + 5}{7}$

Identify the slope of each line.

y = $\displaystyle-\frac{7}{2}x + \frac{3}{2}$

y = mx + b

y = $\displaystyle-\frac{2}{7}x + \frac{5}{7}$

y = mx + b

m₁ = $\displaystyle-\frac{7}{2}$

m₁ = $\displaystyle-\frac{2}{7}$

The slopes are reciprocals of each other, but they have the same sign. Since they are not negative reciprocals, the lines are not perpendicular.

Use slopes to determine if the lines are perpendicular:

a. y = −3x + 2 and x − 3y = 4 b. 5x + 4y = 1 and 4x + 5y = 3.

Solution:

a. perpendicular b. not perpendicular

Use slopes to determine if the lines are perpendicular:

a. y = 2x − 5 and x + 2y = −6 b. 2x − 9y = 3 and 9x − 2y = 1.

Solution:

a. perpendicular b. not perpendicular

Find an Equation of a Line Perpendicular to a Given Line

Suppose we need to find a line passing through a specific point and which is perpendicular to a given line. We can use the fact that perpendicular lines have slopes that are negative reciprocals. We will again use the point-slope equation, like we did with parallel lines.

This graph shows y = 2x − 3. Now, we want to graph a line perpendicular to this line and passing through (−2, 1).

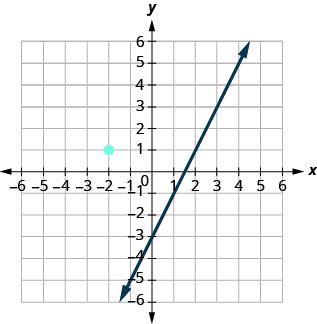
This figure has a graph of a straight line and a point on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (0, negative 3), (1, negative 1), and (2, 1). The point (negative 2, 1) is plotted. The line does not go through the point (negative 2, 1).

We know that perpendicular lines have slopes that are negative reciprocals. We’ll use the notation m_⊥to represent the slope of a line perpendicular to a line with slope m. (Notice that the subscript ⊥ looks like the right angles made by two perpendicular lines.)

y = 2x − 3 perpendicular line
m = 2 m_⊥= $\displaystyle-\frac{1}{2}$

We now know the perpendicular line will pass through (−2, 1) with m_⊥= −12.

To graph the line, we will start at (−2, 1) and count out the rise −1 and the run 2. Then we draw the line.

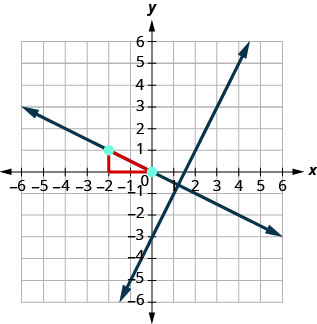
Do the lines appear perpendicular? Does the second line pass through (−2, 1)?

We were asked to graph the line, now, let’s see how to do this algebraically.

We can use either the slope-intercept form or the point-slope form to find an equation of a line. In this example we know one point, and can find the slope, so we will use the point-slope form.

Try it! – How to Find the Equation of a Line Perpendicular to a Given Line and a Point

Find an equation of a line perpendicular to y = 2x − 3 that contains the point (−2, 1). Write the equation in slope-intercept form.

Solution:

Step 2 is to find the slope of the perpendicular line. The slopes of perpendicular lines are negative reciprocals. m equals negative 1 divided by 2

Step 3 is to identify the point. The given point is (negative 2, 1). x 1 is negative 2 and y 1 is 1.

Step 4 is to substitute the values into the point-slope form y minus y 1 equals m times the quantity x minus x 1 in parentheses. y minus 1 equals negative 1 divided by 2 times the quantity x minus negative 2 in parentheses. This simplifies to y minus 1 equals negative 1 divided by 2 times the quantity x plus 2 in parentheses. This further simplifies to y minus 1 equals negative 1 divided by 2 times x minus 1.

Step 5 is to write the equation in slope-intercept form. y equals negative 1 divided by 2 times x.

Find an equation of a line perpendicular to the line y = 3x + 1 that contains the point (4, 2). Write the equation in slope-intercept form.

Solution:

y = −13x + 103

Find an equation of a line perpendicular to the line y = 12x − 3 that contains the point (6, 4). Write the equation in slope-intercept form.

Solution:

y = −2x + 16

Find an equation of a line perpendicular to a given line.

Find the slope of the given line.
Find the slope of the perpendicular line.
Identify the point.
Substitute the values into the point-slope form, y − y₁= m(x − x₁).
Write the equation in slope-intercept form.

Try it!

Find an equation of a line perpendicular to x = 5 that contains the point (3, −2). Write the equation in slope-intercept form.

Solution:

Again, since we know one point, the point-slope option seems more promising than the slope-intercept option. We need the slope to use this form, and we know the new line will be perpendicular to x = 5. This line is vertical, so its perpendicular will be horizontal. This tells us the m_⊥= 0.

Steps

Algebraic

Identify the point.

(3, -2)

Identify the slope of the perpendicular line.

m_⊥= 0.

Substitute the values into y − y₁= m(x − x₁).

y − y₁= m(x − x₁).

Simplify.

y – (-2) = 0(x – 3)

y + 2 = 0

y = -2

Sketch the graph of both lines. On your graph, do the lines appear to be perpendicular?

Find an equation of a line that is perpendicular to the line x = 4 that contains the point (4, −5). Write the equation in slope-intercept form.

Solution:

y = −5

We could have looked at this in a different way. We want to find a line that is perpendicular to x = 5 that contains the point (3,−2). This graph shows us the line x = 5 and the point (3, −2).

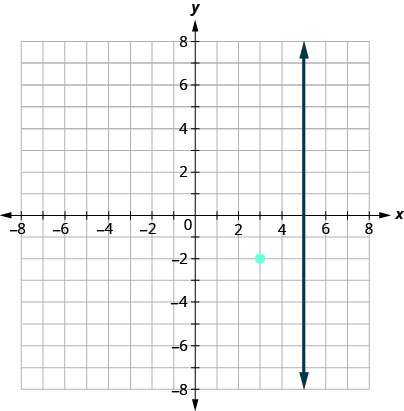
This figure has a graph of a straight vertical line and a point on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (5, 0), (5, 1), and (5, 2). The point (3, negative 2) is plotted. The line does not go through the point (3, negative 2).

We know every line perpendicular to a vertical line is horizontal, so we will sketch the horizontal line through (3, −2).

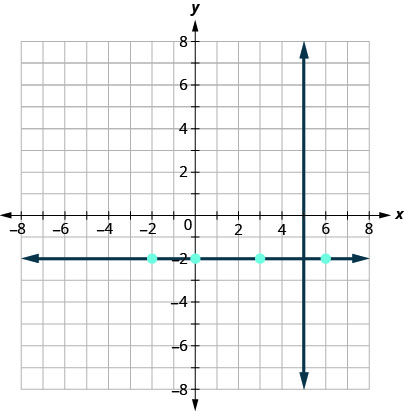
This figure has a graph of a straight vertical line and a straight horizontal line on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The vertical line goes through the points (5, 0), (5, 1), and (5, 2). The horizontal line goes through the points (negative 2, negative 2), (0, negative 2), (3, negative 2), and (6, negative 2).

Do the lines appear perpendicular?

If we look at a few points on this horizontal line, we notice they all have y-coordinates of −2. So, the equation of the line perpendicular to the vertical line x = 5 is y = −2.

Try it!

Find an equation of a line that is perpendicular to y = −3 that contains the point (−3, 5). Write the equation in slope-intercept form.

Solution:

The line y = −3 is a horizontal line. Any line perpendicular to it must be vertical, in the form x=a. Since the perpendicular line is vertical and passes through (−3, 5), every point on it has an x-coordinate of −3. The equation of the perpendicular line is x = −3

You may want to sketch the lines. Do they appear perpendicular?

Find an equation of a line that is perpendicular to the line y = −5 that contains the point (−4, −5). Write the equation in slope-intercept form.

Solution:

x = −4

Access these online resources for additional instruction and practice with finding the equation of a line.

Rate of Change

A rate of change is a relationship or unit rate that shows how one variable or quantity changes with another.

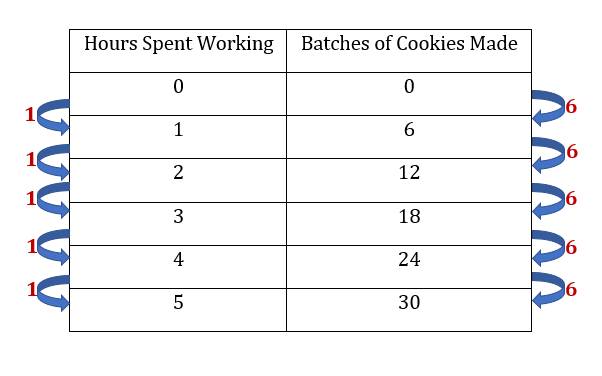
a table with notated changes in x and y values to determine the rate of change. Left column is title hours spent working and has the following values in each row: 0, 1, 2, 3, 4, 5. The 2nd column is titled Batches of cookies made and has the following values: 0, 6, 12, 18, 24, and 30. Arrows on the sides note that the change in x value is 1, the change in y values is 6.

The most common way to investigate rates of change is in numerical or tabular form of data.How the values of x change compared to how the values of y change is called the rate of change. From hour 1 to hour 2, 6 batches of cookies were made. From hour 2 to hour 3, 6 more batches were made. This relationship of change is often represented with a ratio where the dependent variable is in the numerator and the independent variable is in the denominator. The rate of change here would be: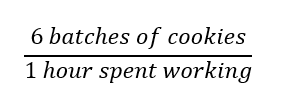 ratio showing 6 batches of cookies over one hours spent working.

Recall from the previous chapter, that slope is sometimes described as rise over run.
We can assign a numerical value to the slope of a line by finding the ratio of the rise and run. The rise is the amount the vertical distance changes while the run measures the horizontal change, as shown in this illustration. Slope is a rate of change.

Slope reminder

The slope of a line, m, represents the vertical change in y over the horizontal change in x. Given two points, (x₁, y₁) and (x₂, y₂), the following formula determines the slope of a line containing these points:

m = $\displaystyle\frac{y_2 - y_1}{x_2 - x_1}$

Slope also indicates the direction in which a line slants as well as its steepness.

So rate of change describes how an output quantity changes relative to the change in the input quantity. To find the average rate of change over the specified period of time, we divide the change in the output value by the change in the input value.

Steps

Algebraic

Forms of Average rate of change (Slope)

= $\displaystyle\frac{\text{Change in output}}{\text{Change in input}}$ .

= $\displaystyle\frac{\Delta y}{\Delta x}$

= $\displaystyle\frac{y_2 - y_1}{x_2 - x_1}$

= $\displaystyle\frac{f(x_2) - f(x_1)}{x_2 - x_1}$

The Greek letter Δ (delta) signifies the change in a quantity; we read the ratio as “delta-y over delta-x” or “the change in y divided by the change in x.” Occasionally we write Δf instead of Δy, which still represents the change in the function’s output value resulting from a change to its input value. It does not mean we are changing the function into some other function.

Try it!

Gasoline costs have experienced some wild fluctuations over the last several decades. The table lists the average cost, in dollars, of a gallon of gasoline for the years 2005 – 2012. The cost of gasoline can be considered as a function of year.

Example

y

2005

2006

2007

2008

2009

2010

2011

2012

C(y)

2.31

2.62

2.84

3.30

2.41

2.84

3.58

3.68

Solution:

If we were interested only in how the gasoline prices changed between 2005 and 2012, we could compute that the cost per gallon had increased from $2.31 to $3.68, an increase of $1.37. While this is interesting, it might be more useful to look at how much the price changed per year.

In our example, the gasoline price increased by $1.37 from 2005 to 2012. Over 7 years, the average rate of change was

$\displaystyle\frac{\Delta y}{\Delta x} = \frac{\$1.37}{7 \text{years}}$ ≈ 0.196 dollars per year

On average, the price of gas increased by about 19.6¢ each year.

Other examples of rates of change include:

A population of rats increasing by 40 rats per week
A car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
A car driving 27 miles per gallon (distance traveled changes by 27 miles for each gallon)
The current through an electrical circuit increasing by 0.125 amperes for every volt of increased voltage
The amount of money in a college account decreasing by $4,000 per quarter

Rate of Change

A rate of change describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are “output units per input units.”

The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.

$\displaystyle\frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1}$

Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values x₁ and x₂.

Calculate the difference y₂ – y₁ = Δy.
Calculate the difference x₂ – x₁ = Δx.
Find the ratio $\displaystyle\frac{\Delta y}{\Delta x}$

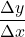
Try it! – Computing an Average Rate of Change

Using the data in the table below, find the average rate of change of the price of gasoline between 2007 and 2009.

Example

y

2005

2006

2007

2008

2009

2010

2011

2012

C(y)

2.31

2.62

2.84

3.30

2.41

2.84

3.58

3.68

Solution:

In 2007, the price of gasoline was $2.84. In 2009, the cost was $2.41. The average rate of change is

$\displaystyle\frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1}$

$\displaystyle = \frac{\$2.41 - \$2.84}{2009 - 2007}$

$\displaystyle = \frac{-\$0.43 }{2 \text{years}}$

= -$0.22 per year

Analysis

Note that a decrease is expressed by a negative change or “negative increase.” A rate of change is negative when the output decreases as the input increases or when the output increases as the input decreases.

Try it! – Computing Average Rate of Change for a Function Expressed as a Formula

Compute the average rate of change of $\displaystyle f(x) = x^2 - \frac{1}{x}$ on the interval [2, 4].

Solution:

We can start by computing the function values at each endpoint of the interval.

Algebraic

$\displaystyle f(2) = 2^2 - \frac{1}{2}$

$\displaystyle f(4) = 4^2 - \frac{1}{4}$

$\displaystyle = 4 - \frac{1}{2}$

$\displaystyle = 16 - \frac{1}{4}$

$\displaystyle = \frac{7}{2}$

$\displaystyle = \frac{63}{4}$

Now we compute the average rate of change.

Steps

Algebraic

Average rate of change

$\displaystyle = \frac{f(4) - f(2)}{4 - 2}$

$\displaystyle = \frac{\frac{63}{4} - \frac{7}{2}}{4 - 2}$

$\displaystyle = \frac{\frac{49}{4}}{2}$

$\displaystyle = \frac{f49}{8}$

Find the average rate of change $\displaystyle f(x) = x - 2\sqrt{x}$ of on the interval [1, 9].

Solution:

$\displaystyle\frac{1}{2}$

Try it! – Computing Average Rate of Change from a Graph

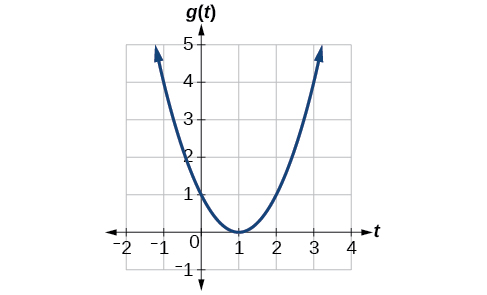
Given the function g(t) shown in [link], find the average rate of change on the interval [−1, 2].

Graph of a parabola with vertex at (1, 0) and crosses the y axis at (0,1)

Solution:

At t = −1,[link] shows g(−1) = 4. At t = 2, the graph shows g(2) = 1.

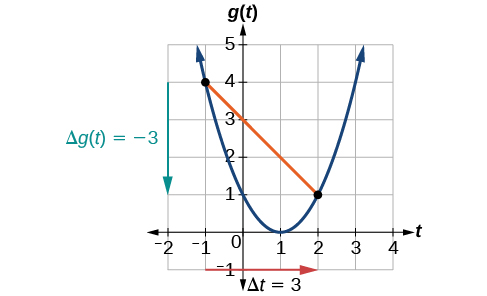
Graph of a parabola with a line from points (-1, 4) and (2, 1) to show the changes for g(t) and t.

The horizontal change Δt = 3 is shown by the red arrow, and the vertical change Δg(t) = −3 is shown by the turquoise arrow. The average rate of change is shown by the slope of the orange line segment. The output changes by –3 while the input changes by 3, giving an average rate of change of

$\displaystyle\frac{1 - 4}{2 - (-1)} = \frac{-3}{3} = -1$

Analysis

Note that the order we choose is very important. If, for example, we use $\displaystyle\frac{f(x_2) - f(x_1)}{x_2 - x_1}$ , we will not get the correct answer. Decide which point will be 1 and which point will be 2, and keep the coordinates fixed as (x₁, y₁) and (x₂, y₂).

Try it! – Computing Average Rate of Change from a Table

After picking up a friend who lives 10 miles away and leaving on a trip, Anna records her distance from home over time. The values are shown in the table below. Find her average speed over the first 6 hours.

*Example*
t (hours)	0	1	2	3	4	5	6	7
D(t) (miles)	10	55	90	153	214	240	292	300

Solution:

Here, the average speed is the average rate of change. She traveled 282 miles in 6 hours.

$\displaystyle\frac{292 - 10}{6 - 0} = \frac{282}{6}$

= 47

The average speed is 47 miles per hour.

Analysis

Because the speed is not constant, the average speed depends on the interval chosen. For the interval [2,3], the average speed is 63 miles per hour.

Try it! – Finding an Average Rate of Change as an Expression

Find the average rate of change of g(t) = t² + 3t + 1 on the interval [0, a]. The answer will be an expression involving a in simplest form.

Solution:

We use the average rate of change formula.

Algebraic

Steps

Average rate of change

$\displaystyle = \frac{g(a) - g(0)}{a - 0}$

Evaluate.

$\displaystyle = \frac{(a^2 + 3a + 1) - (0^2 + 3(0) + 1}{a - 0}$

Simplify.

$\displaystyle = \frac{a^2 + 3a + 1 - 1}{a}$

Simplify and factor.

$\displaystyle = \frac{a(a + 3)}{a}$

Divide by the common factor a.

= a + 3

This result tells us the average rate of change in terms of a between t = 0 and any other point t = a. For example, on the interval [0, 5], the average rate of change would be 5 + 3 = 8.

Find the average rate of change of f(x)=x² + 2x − 8 on the interval [5, a] in simplest forms in terms of a.

Solution:

a + 7

Access this online resource for additional instruction and practice with rates of change.

Average Rate of Change

Key Concepts

Parallel Lines
- Parallel lines are lines in the same plane that do not intersect.
  Parallel lines have the same slope and different y-intercepts.
  If m₁ and m₂are the slopes of two parallel lines then m₁ = m₂.
- Parallel vertical lines have different x-intercepts.
Perpendicular Lines
- Perpendicular lines are lines in the same plane that form a right angle.
- If m₁ and m₂ are the slopes of two perpendicular lines, then:
  - their slopes are negative reciprocals of each other, m₁= – $\displaystyle\frac{1}{m_2}$ .
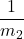  - the product of their slopes is −1, m₁ · m₂ = −1.
- A vertical line and a horizontal line are always perpendicular to each other.

How to find an equation of a line parallel to a given line.
1. Find the slope of the given line.
2. Find the slope of the parallel line.
3. Identify the point.
4. Substitute the values into the point-slope form: y − y₁= m(x − x₁).
5. Write the equation in slope-intercept form
How to find an equation of a line perpendicular to a given line.
1. Find the slope of the given line.
2. Find the slope of the perpendicular line.
3. Identify the point.
4. Substitute the values into the point-slope form, y − y₁= m(x − x₁).
5. Write the equation in slope-intercept form.

Average rate of change

$\displaystyle\frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1}$

A rate of change relates a change in an output quantity to a change in an input quantity. The average rate of change is determined using only the beginning and ending data.
Identifying points that mark the interval on a graph can be used to find the average rate of change.
Comparing pairs of input and output values in a table can also be used to find the average rate of change.
An average rate of change can also be computed by determining the function values at the endpoints of an interval described by a formula.
The average rate of change can sometimes be determined as an expression

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Identify and Graph Parallel Lines

Find an Equation of a Line Parallel to a Given Line

Identify and Graph Perpendicular Lines

Find an Equation of a Line Perpendicular to a Given Line

Rate of Change

License

Share This Book