20 Quadratic Equations
Topics Covered
In case you missed something in class, or just want to review a specific topic covered in this Module, here is a list of topics covered:
- Brief Overview of Polynomial Equations
- Zero Product Property
- Solve Quadratic Equations by Factoring
- Solve Quadratic Equations of the form ax2 = k using the Square Root Property
- Solve Quadratic Equations of the form a(x − h)2 = k Using the Square Root Property
- Solve Quadratic Equations using Quadratic Formula
- Discriminant
- Pythagorean Theorem
- Key Concepts
Brief Overview of Polynomial Equations
We have spent considerable time learning how to factor polynomials. We will now look at polynomial equations and solve them using factoring, if possible.
A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.
Polynomial Equation
A polynomial equation is an equation that contains a polynomial expression.
The degree of the polynomial equation is the degree of the polynomial.
We have already solved polynomial equations of degree one. Polynomial equations of degree one are linear equations and of the form ax + b = c.
We are now going to solve polynomial equations of degree two. A polynomial equation of degree two is called a quadratic equation. Listed below are some examples of quadratic equations:
| Ex. 1 | Ex. 2 | Ex. 3 | Ex. 4 |
| x2 + 5x + 6 = 0 | 3y2 + 4y = 10 | 64u2 − 81 = 0 | n(n + 1) = 42 |
The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get n2 + n.
Quadratic Equation
An equation of the form ax2 + bx + c = 0 is called a quadratic equation.
a, b, and c are real numbers and a≠0
(If a = 0, then 0 · x2 = 0 and we are left with no quadratic term.)
Quadratic equations differ from linear equations by including a quadratic term with the variable raised to the second power of the form ax2. We use different methods to solve quadratic equations than linear equations, because just adding, subtracting, multiplying, and dividing terms will not isolate the variable.
Zero Product Property
We will first solve some quadratic equations by using the Zero Product Property. The Zero Product Property says that if the product of two quantities is zero, then at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.
Zero Product Property
If a · b = 0, then either a = 0 or b = 0 or both.
We will now use the Zero Product Property, to solve a quadratic equation.
- Set each factor equal to zero.
- Solve the linear equations.
- Check.
Try it! – How to Solve a Quadratic Equation Using the Zero Product Property
Solve: (5n − 2)(6n − 1) = 0.
Solution



Solve Quadratic Equations by Factoring
The Zero Product Property works very nicely to solve quadratic equations. The quadratic equation must be factored, with zero isolated on one side. So we start with the quadratic equation in standard form, ax2 + bx + c = 0. Then we factor the expression on the left.
- Write the quadratic equation in standard form, ax2 + bx + c = 0.
- Factor the quadratic expression.
- Use the Zero Product Property.
- Solve the linear equations.
- Check. Substitute each solution separately into the original equation.
Before we factor, we must make sure the quadratic equation is in standard form.
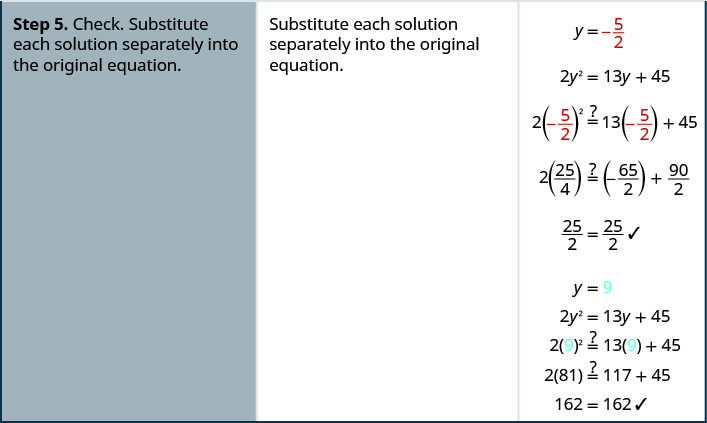
Try it! – How to Solve a Quadratic Equation by Factoring
Solve: 2y2 = 13y + 45.
Solution

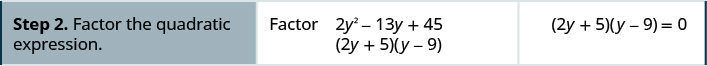


Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in earlier sections! Do you recognize the special product pattern in the next example?
Try it!
Solve: 169q2 = 49.
Solution
| Steps | Algebraic | |
| Write the quadratic equation in standard form. | 169q2 – 49 = 0 | NA |
| Factor. It is a difference of squares. | (13q – 7) (13q + 7) = 0 | NA |
| Use the Zero Product Property to set each factor to 0. | 13q – 7 = 0 |
13q + 7 = 0 |
| Solve each equation. | 13q = 7 | 13q = -7 |
| Solutions | q = |
q = – |
|
Check: We leave the check up to you. |
||
Try it!
Solve: (3x − 8)(x − 1) = 3x.
Solution
| Steps | Algebraic | |
| Equation | (3x − 8)(x − 1) = 3x |
|
| Multiply the binomials. | 3x2 − 11x + 8 = 3x |
|
| Write the quadratic equation in standard form. | 3x2 − 14x + 8 = 0 |
|
| Factor the trinomial. | (3x − 2)(x − 4) = 0 |
|
| Use the Zero Product Property to set each factor to 0 | 3x − 2 = 0 | x − 4 = 0 |
| Solve each equation | 3x = 2 | x = 4 |
|
Check your answers. |
The check is left to you. | |
In the next example, when we factor the quadratic equation, we will get three factors. However, the first factor is a constant. We know that factor cannot equal 0.
Try it!
Solve: 3x2 = 12x + 63.
Solution
| Steps | Algebraic |
| Equation | 3x2 = 12x + 63 |
| Write the quadratic equation in standard form. | 3x2 − 12x − 63 = 0 |
| Factor the greatest common factor first. | 3(x2 − 4x − 21) = 0 |
| Factor the trinomial. | 3(x − 7)(x + 3) = 0 |
| Use the Zero Product Property to set each factor to 0. | 3 ≠ 0 x − 7 = 0 x + 3 = 0 |
| Solve each equation. | 3 ≠ 0 x = 7 x = −3 |
| Check your answers. | The check is left to you. |
Solve Quadratic Equations of the form ax2 = k using the Square Root Property
We have already solved some quadratic equations by factoring. Let’s review how we used factoring to solve the quadratic equation x2 = 9.
| Steps | Algebraic |
| Equation | x2 = 9 |
| Put the equation in standard form. | x2 − 9 = 0 |
| Factor the difference of squares. | (x − 3)(x + 3) = 0 |
| Use the Zero Product Property. | x − 3 = 0 and x + 3 = 0 |
| Solve each equation. | x = 3 and x = −3 |
We can easily use factoring to find the solutions of similar equations, like x2 = 16 and x2 = 25, because 16 and 25 are perfect squares. In each case, we would get two solutions, x = 4, x = −4 and x = 5, x = −5.
But what happens when we have an equation like x2 = 7? Since 7 is not a perfect square, we cannot solve the equation by factoring.
Previously we learned that since 169 is the square of 13, we can also say that 13 is a square root of 169. Also, (−13)2 = 169, so −13 is also a square root of 169. Therefore, both 13 and −13 are square roots of 169. So, every positive number has two square roots—one positive and one negative. We earlier defined the square root of a number in this way:
Since these equations are all of the form x2 = k, the square root definition tells us the solutions are the two square roots of k. This leads to the Square Root Property.
Square Root Property
If x2 = k, then
x = ![]() or x = −
or x = −![]() or x = ±
or x = ±![]() .
.
Notice that the Square Root Property gives two solutions to an equation of the form x2 = k, the principal square root of k and its opposite. We could also write the solution as x = ±![]() . We read this as x equals positive or negative the square root of k.
. We read this as x equals positive or negative the square root of k.
Now we will solve the equation x2 = 9 again, this time using the Square Root Property.
| Algebraic |
| x2 = 9 |
| x = ± |
| x = ±3 |
| So x = 3 or x = −3. |
What happens when the constant is not a perfect square? Let’s use the Square Root Property to solve the equation x2 = 7.
| Algebraic |
| x2 = 7 |
| x = |
We cannot simplify [latex]\sqrt{7}[/latex], so we leave the answer as a radical.
- Isolate the quadratic term and make its coefficient one.
- Use Square Root Property.
- Simplify the radical.
- Check the solutions.
Try it!
Solve: x2 − 50 = 0.




In order to use the Square Root Property, the coefficient of the variable term must equal one. In the next example, we must divide both sides of the equation by the coefficient 3 before using the Square Root Property.
Try it!
Solve: 3z2 = 108.
Solution
| Steps | Algebraic |
| Equation | 3z2 = 108 |
| The quadratic term is isolated. Divide by 3 to make its coefficient 1. |
|
| Simplify. | z2 = 36 |
| Use the Square Root Property. | z = ± |
| Simplify the radical. | z = ±6 |
| Rewrite to show two solutions. | z = 6, z = −6 |
| Check the solutions: |
 |
The Square Root Property states ‘If x2 = k,’ What will happen if k < 0? This will be the case in the next example.
Try it!
Solve: x2 + 72 = 0
Solution
| Steps | Algebraic |
| Equation | x2 + 72 = 0 |
| Isolate the quadratic term. | x2 = −72 |
| Use the Square Root Property. | x = ± |
| Simplify using complex numbers. | x = ± |
| Simplify the radical. | x = ±6 |
| Rewrite to show two solutions. | x = 6 |
| Check the solutions: |
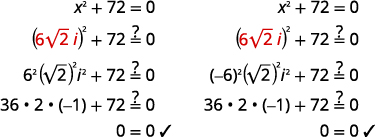 |
Our method also works when fractions occur in the equation, we can solve any equation with fractions. In the next example, we first isolate the quadratic term, and then make the coefficient equal to one.
Try it!
Solve: ![]() u2 + 5 = 17.
u2 + 5 = 17.
Solution
| Steps | Algebraic |
| Equation | |
| Isolate the quadratic term. | |
| Multiply by |
|
| Simplify. | |
| Use the Square Root Property. | |
| Simplify the radical. | |
| Simplify. | |
| Rewrite to show two solutions. | |
| Check: |
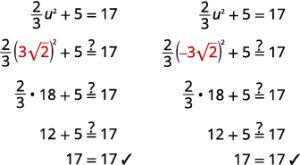 |
The solutions to some equations may have fractions inside the radicals. When this happens, we must rationalize the denominator.
Try it!
Solve: 2x2 − 8 = 41.
Solution
| Steps | Algebraic |
| Equation | 2x2 − 8 = 41 |
| Isolate the quadratic term. | |
| Divide by 2 to make the coefficient 1. | |
| Simplify. | |
| Use the Square Root Property. | |
| Rewrite the radical as a fraction of square roots. | |
| Rationalize the denominator. | |
| Simplify. | |
| Rewrite to show two solutions. | |
| Check: | We leave the check for you. |
Solve Quadratic Equations of the form a(x – h)2 = k using the Square Root Property
We can use the Square Root Property to solve an equation of the form a(x − h)2 = k as well. Notice that the quadratic term, x, in the original form ax2 = k is replaced with (x − h).
![]() The first step, like before, is to isolate the term that has the variable squared. In this case, a binomial is being squared. Once the binomial is isolated, by dividing each side by the coefficient of a, then the Square Root Property can be used on (x − h)2.
The first step, like before, is to isolate the term that has the variable squared. In this case, a binomial is being squared. Once the binomial is isolated, by dividing each side by the coefficient of a, then the Square Root Property can be used on (x − h)2.
Try it!
Solve: 4(y − 7)2 = 48
Solution
| Steps | Algebraic |
| Equation | 4(y − 7)2 = 48 |
| Divide both sides by the coefficient 4. | (y − 7)2 = 12 |
| Use the Square Root Property on the binomial | y − 7 = ± |
| Simplify the radical. | y − 7 = ±2 |
| Solve for y. | y = 7 ± 2 |
| Rewrite to show two solutions. | y = 7 + 2 |
| Check: |
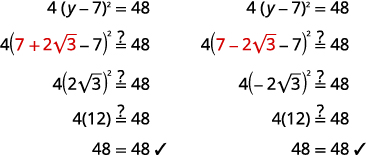 |
Remember when we take the square root of a fraction, we can take the square root of the numerator and denominator separately.
Try it!
Solve: ![]() .
.
Solution
| Steps | Algebraic |
| Equation | |
| Use the Square Root Property. | x − |
| Rewrite the radical as a fraction of square roots. | x − |
| Simplify the radical. | x − |
| Solve for x. | x = |
| Rewrite to show two solutions. | x = |
| Check: | We leave the check for you. |
Sometimes the solutions are complex numbers.
Try it!
Solve: (2x − 3)2 = −12.
Solution
| Steps | Algebraic |
| Equation | (2x − 3)2 = −12 |
| Use the Square Root Property. | 2x – 3 = ± |
| Simplify the radical. | 2x – 3 = ± 2 |
| Add 3 to both sides. | 2x = 3 ± 2 |
| Divide both sides by 2. | x = |
| Rewrite in standard form. | x = |
| Simplify. | x = |
| Rewrite to show two solutions. | x = |
| Check: | We leave the check for you. |
The left sides of the equations in the next two examples do not seem to be of the form a(x − h)2. But they are perfect square trinomials, so we will factor to put them in the form we need.
Try it!
Solve: 4n2 + 4n + 1 = 16.
Solution
We notice that the left side of the equation is a perfect square trinomial. We will factor it first.
| Steps | Algebraic |
| Equation | 4n2 + 4n + 1 = 16 |
| Factor the perfect square trinomial. | (2n + 1)2 = 16 |
| Use the Square Root Property. | 2n + 1 = ± |
| Simplify the radical. | 2n + 1 = ±4 |
| Solve for n. | 2n = −1 ± 4 |
| Divide each side by 2. | |
| n = |
|
| Rewrite to show two solutions. | n = |
| Simplify each equation. | n = |
| Check: |
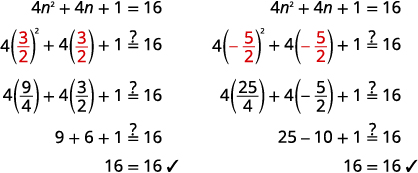 |
Access this online resource for additional instruction and practice with using the Square Root Property to solve quadratic equations.
Solve Quadratic Equations using Quadratic Formula
When we solved quadratic equations in the last section by completing the square, we took the same steps every time. By the end of the exercise set, you may have been wondering ‘isn’t there an easier way to do this?’ The answer is ‘yes’. Mathematicians look for patterns when they do things over and over in order to make their work easier. In this section we will derive and use a formula to find the solution of a quadratic equation.
We start with the standard form of a quadratic equation and solve it for x by completing the square.
| Steps | Algebraic |
| Isolate the variable terms on one side. | |
| Make the coefficient of x2 equal to 1, by dividing by a. |
|
| Simplify. | |
| To complete the square, find |
|
| The left side is a perfect square, factor it. | |
| Find the common denominator of the right side and write equivalent fractions with the common denominator. |
|
| Simplify. | |
| Combine to one fraction. | |
| Use the square root property. | |
| Simplify the radical. | |
| Add |
|
| Combine the terms on the right side. | |
| This equation is the Quadratic Formula. | |
The solutions to a quadratic equation of the form ax2 + bx + c = 0, where a ≠ 0 are given by the formula:
How to solve quadratic equations using the quadratic formula
- Write the quadratic equation in standard form, ax2 + bx + c = 0. Identify the values of a, b, and c.
- Write the Quadratic Formula. Then substitute in the values of a, b, and c.
- Simplify.
- Check the solutions.
Try it!
- Solve by using the Quadratic Formula: 2x2 + 9x − 5 = 0.
Solution


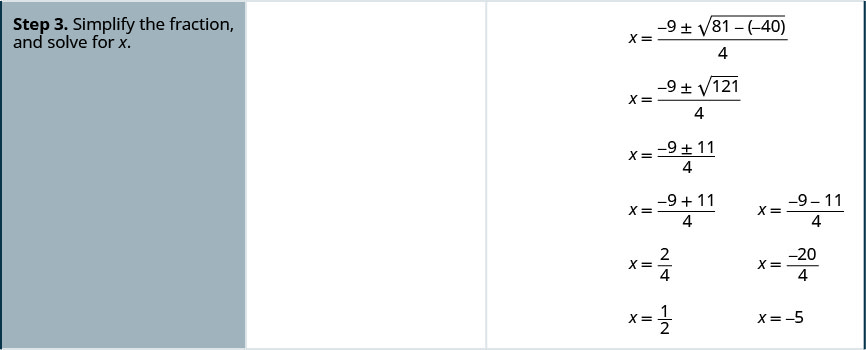

2. Solve by using the Quadratic Formula: x2 − 6x = −5.
Solution
| Steps | Algebraic |
| Equation | |
| Write the equation in standard form by adding 5 to each side. |
|
| This equation is now in standard form. | |
| Identify the values of a, b, c. | |
| Write the Quadratic Formula. | |
| Then substitute in the values of a, b, c. | |
| Simplify. | |
| Rewrite to show two solutions. | |
| Simplify. | |
| Solution | |
| Check: | 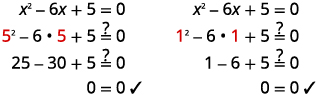 |
When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That can happen, too, when using the Quadratic Formula. If we get a radical as a solution, the final answer must have the radical in its simplified form.
Try it!
Solve by using the Quadratic Formula: 2x2 + 10x + 11 = 0.
Solution
| Steps | Algebraic |
| Equation | |
| This equation is in standard form. | |
| Identify the values of a, b, and c. | |
| Write the Quadratic Formula. | |
| Then substitute in the values of a, b, and c. | |
| Simplify. | |
| Simplify the radical. | |
| Factor out the common factor in the numerator. | |
| Remove the common factors. | |
| Rewrite to show two solutions. | |
| Check: | We leave the check for you! |
When we substitute a, b, and c into the Quadratic Formula and the radicand is negative, the quadratic equation will have imaginary or complex solutions. We will see this in the next example.
Try it!
Solve by using the Quadratic Formula: 3p2 + 2p + 9 = 0.
Solution
| Steps | Algebraic |
| Equation | |
| This equation is in standard form | |
| Identify the values of a, b, c. | |
| Write the Quadratic Formula. | |
| Then substitute in the values of a, b, c. | |
| Simplify. | |
| Simplify the radical using complex numbers. | |
| Simplify the radical. | |
| Factor the common factor in the numerator. | |
| Remove the common factors. | |
| Rewrite in standard a + bi form. | |
| Write as two solutions. |
Discriminant
When we solved the quadratic equations in the previous examples, sometimes we got two real solutions, one real solution, and sometimes two complex solutions. Is there a way to predict the number and type of solutions to a quadratic equation without actually solving the equation?
Yes, the expression under the radical of the Quadratic Formula makes it easy for us to determine the number and type of solutions. This expression is called the discriminant.
Discriminant
Let’s look at the discriminant of the equations in some of the examples and the number and type of solutions to those quadratic equations. The quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions when we consider the discriminant, or the expression under the radical, b2 − 4ac. The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. The table below relates the value of the discriminant to the solutions of a quadratic equation.

| Value of Discriminant | Results |
|---|---|
| b2 − 4ac = 0 | One rational solution (double solution) |
| b2 − 4ac > 0, perfect square | Two rational solutions |
| b2 − 4ac > 0, not a perfect square | Two irrational solutions |
| b2 − 4ac < 0 | Two complex solutions |
Try it!
- Determine the number of solutions to each quadratic equation.
a. 3x2 + 7x − 9 = 0 b. 5n2 + n + 4 = 0 c. 9y2 − 6y + 1 = 0.
Solution
To determine the number of solutions of each quadratic equation, we will look at its discriminant.
a.
| Steps | Algebraic |
| Equation | 3x2 + 7x − 9 = 0 |
| The equation is in standard form, identify a, b, and c. | a = 3, b = 7, c = −9 |
| Write the discriminant. | b2 − 4ac |
| Substitute in the values of a, b, and c. | (7)2 − 4 · 3 · (−9) |
| Simplify. | 49 + 108 |
| Solution | 157 |
Since the discriminant is positive, there are 2 real solutions to the equation.
b.
| Steps | Algebraic |
| Equation | 5n2 + n + 4 = 0 |
| The equation is in standard form, identify a, b, and c. | a = 5, b = 1, c = 4 |
| Write the discriminant. | b2 − 4ac |
| Substitute in the values of a, b, and c. | (1)2 – 4 · 5 · 4 |
| Simplify. | 1 – 80 |
| Solution | -79 |
Since the discriminant is negative, there are 2 complex solutions to the equation.
c.
| Steps | Algebraic |
| Equation | 9y2 − 6y + 1 = 0 |
| The equation is in standard form, identify a, b, and c. | a = 9, b = −6, c = 1 |
| Write the discriminant. | b2 − 4ac |
| Substitute in the values of a, b, and c. | (-6)2 – 4 · 9 · 1 |
| Simplify. | 36 – 36 |
| Solution | 0 |
Since the discriminant is 0, there is 1 real solution to the equation.
2. For each Equation, compute the determinant and determine the number and type of solution.
- x2 + 4x + 4 = 0
- 8x2 + 14x + 3 = 0
- 3x2 − 5x − 2 = 0
- 3x2 − 10x + 15 = 0
Solution:
Calculate the discriminant b2 − 4ac for each equation and state the expected type of solutions.
-
x2 + 4x + 4 = 0
b2 − 4ac = (4)2 − 4(1)(4) = 0.
There will be one rational double solution.
-
8x2 + 14x + 3 = 0
b2 − 4ac = (14)2 − 4(8)(3) = 100.
As 100 is a perfect square, there will be two rational solutions.
-
3x2 − 5x − 2 = 0
b2 − 4ac = (−5)2 − 4(3)(−2) = 49.
As 49 is a perfect square, there will be two rational solutions.
-
3x2 − 10x + 15 = 0
b2 − 4ac = (−10)2 − 4(3)(15) = −80.
There will be two complex solutions.
Identify the Most Appropriate Method to Use to Solve a Quadratic Equation
Given that we have four methods to use to solve a quadratic equation, how do you decide which one to use? Factoring is often the quickest method and so we try it first. If the equation is ax2 = k or a(x − h)2 = k we use the Square Root Property. For any other equation, it is probably best to use the Quadratic Formula. Remember, you can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method.
Try it!
Identify the most appropriate method to use to solve each quadratic equation.
a. 5z2 = 17 b. 4x2 − 12x + 9 = 0 c. 8u2 + 6u = 11.
Solution:
a. 5z2 = 17
Since the equation is in the ax2 = k, the most appropriate method is to use the Square Root Property.
b. 4x2 − 12x + 9 = 0
We recognize that the left side of the equation is a perfect square trinomial, and so factoring will be the most appropriate method.
c.
| Steps | Algebraic |
| Equation | 8u2 + 6u = 11 |
| Put the equation in standard form. | 8u2 + 6u − 11 = 0 |
While our first thought may be to try factoring, thinking about all the possibilities for trial and error method leads us to choose the Quadratic Formula as the most appropriate method.
Access these online resources for additional instruction and practice with using the Quadratic Formula.
Pythagorean Theorem
One of the most famous formulas in mathematics is the Pythagorean Theorem. It is based on a right triangle, and states the relationship among the lengths of the sides as a2 + b2 = c2, where a and b refer to the legs of a right triangle adjacent to the 90° angle, and c refers to the hypotenuse. It has immeasurable uses in architecture, engineering, the sciences, geometry, trigonometry, and algebra, and in everyday applications.
We use the Pythagorean Theorem to solve for the length of one side of a triangle when we have the lengths of the other two. Because each of the terms is squared in the theorem, when we are solving for a side of a triangle, we have a quadratic equation. We can use the methods for solving quadratic equations that we learned in this section to solve for the missing side.
The Pythagorean Theorem is given as
a2 + b2 = c2
where a and b refer to the legs of a right triangle adjacent to the 90° angle, and c refers to the hypotenuse, as shown below.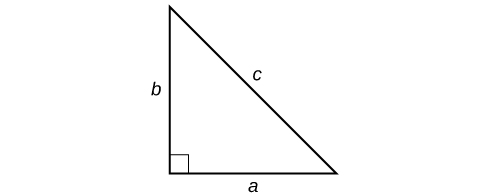
Try it! – Finding the Length of the Missing Side of a Right Triangle
Find the length of the missing side of the right triangle
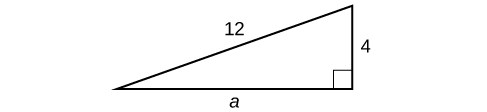
Solution
As we have measurements for side b and the hypotenuse, the missing side is a.
| Algebraic |
| a2 + b2 = c2 |
| a2 + (4)2 = (12)2 |
| a2 + 16 = 144 |
| a2 = 128 |
Key Concepts
- Polynomial Equation: A polynomial equation is an equation that contains a polynomial expression. The degree of the polynomial equation is the degree of the polynomial.
- Quadratic Equation: An equation of the form ax2 + bx + c = 0 is called a quadratic equation. a, b, and c are real numbers and a ≠ 0 .
- Zero Product Property: If If a · b = 0, then either a = 0 or b = 0 or both.
- How to use the Zero Product Property
- Set each factor equal to zero.
- Solve the linear equations.
- Check.
- How to solve a quadratic equation by factoring.
- Write the quadratic equation in standard form, ax2 + bx + c = 0.
- Factor the quadratic expression.
- Use the Zero Product Property.
- Solve the linear equations.
- Check. Substitute each solution separately into the original equation.
- Square Root Property
- If x2 = k, then
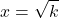 or
or 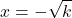 or
or 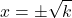 .
.
- If x2 = k, then
- How to solve a quadratic equation using the square root property.
- Isolate the quadratic term and make its coefficient one.
- Use Square Root Property.
- Simplify the radical.
- Check the solutions.
- Quadratic Equation: The solutions to a quadratic equation of the form ax2 + bx + c = 0, where a ≠ 0 are given by the formula:
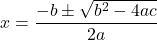
- Using the Discriminant, b2 − 4ac, to Determine the Number and Type of Solutions of a Quadratic Equation
- For a quadratic equation of the form ax2 + bx + c = 0, a ≠ 0,
- If b2 − 4ac > 0, the equation has 2 real solutions.
- if b2 − 4ac = 0, the equation has 1 real solution.
- if b2 − 4ac < 0, the equation has 2 complex solutions.
- For a quadratic equation of the form ax2 + bx + c = 0, a ≠ 0,

