11 Applications and Modeling
Topics Covered
Use a Problem-Solving Strategy for Word Problems
Have you ever had any negative experiences in the past with word problems? When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. Realize that your negative experiences with word problems are in your past. To move forward you need to calm your fears and change your negative feelings.
Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using proper algebra techniques.
- Check the answer in the problem to make sure it makes sense.
- Answer the question with a complete sentence.
When dealing with real-world applications, there are certain expressions that we can translate directly into math. The table lists some common verbal expressions and their equivalent mathematical expressions.
| Verbal | Translation to Math Operations |
|---|---|
| One number exceeds another by a | x, x + a |
| Twice a number | 2x |
| One number is a more than another number | x, x + a |
| One number is a less than twice another number | x, 2x − a |
| The product of a number and a, decreased by b | ax − b |
| The quotient of a number and the number plus a is three times the number | |
| The product of three times a number and the number decreased by b is c | 3x(x − b) = c |
Try it!
Normal yearly snowfall at the local ski resort is 12 inches more than twice the amount it received last season. The normal yearly snowfall is 62 inches. What was the snowfall last season at the ski resort?
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what you are looking for. | What was the snowfall last season? |
| 3. Name what we are looking for and choose a variable to represent it. |
Let s = the snowfall last season. |
| 4. Translate. Restate the problem in one sentence with all the important information. |
|
| Translate into an equation. | |
| 5. Solve the equation. | |
| Subtract 12 from each side. | |
| Simplify. | |
| Divide each side by two. | |
| Simplify. | |
| 6. Check: First, is our answer reasonable?
Yes, having 25 inches of snow seems OK. |
|
| 7. Answer the question. | The snowfall last season was 25 inches. |
2. A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what you are looking for. | How much does the husband earn? |
| 3. Name.
Choose a variable to represent the amount the husband earns. The wife earns $16,000 less than twice that. |
Let h = the amount the husband earns. |
| 4. Translate.
Restate the problem in one sentence with all the important information. Translate into an equation. |
2h − 16,000 = the amount the wife earns.
Together the husband and wife earn $110,000. |
| 5. Solve the equation.
Combine like terms. Add 16,000 to both sides and simplify. Divide each side by three.
|
h + 2h − 16,000 = 110,000
h + 2h − 16,000 = 110,000 3h − 16,000 = 110,000 3h = 126,000 h = 42,000 $42,000 amount husband earns 2h − 16,000 amount wife earns 2(42,000) − 16,000 84,000 − 16,000 68,000 |
| 6. Check:
If the wife earns $68,000 and the husband earns $42,000, is that $110,000? |
Yes! |
| 7. Answer the question. | The husband earns $42,000 a year |
Access this online resource for additional instruction and practice with using a problem-solving strategy.
Solve Percent Applications
How many cents are in one dollar? There are 100 cents in a dollar. How many years are in a century? There are 100 years in a century. Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is 100. We use the percent symbol %, to show percent.
A percent is a ratio whose denominator is 100.
Similarly, 25% means a ratio of ![]() , 3% means a ratio of
, 3% means a ratio of ![]() , and 100% means a ratio of
, and 100% means a ratio of ![]() . In words, “one hundred percent” means the total 100% is
. In words, “one hundred percent” means the total 100% is ![]() , and since
, and since ![]() = 1, we see that 100% means 1 whole.
= 1, we see that 100% means 1 whole.
There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.
How to convert a percent number to a decimal number
To convert a percent number to a decimal number, we move the decimal point two places to the left and remove the % sign. (Sometimes the decimal point does not appear in the percent number, but just like we can think of the integer 6 as 6.0, we can think of 6% as 6.0%. Notice that we may need to add zeros in front of the number when moving the decimal to the left.
- Write the percent as a ratio with the denominator 100.
- Convert the fraction to a decimal by dividing the numerator by the denominator.
Try it!
- Convert each percent to a decimal:
a. 135%
b. 12.5%
Solution
a.
| Steps | Algebraic |
| Example | 135% |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 1.35 |
b.
| Steps | Algebraic |
| Example | 12.5% |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.125 |
2. Translate and solve:
a. What number is 45% of 84?
b. 8.5% of what amount is $4.76?
Solution
a.
| Steps | Algebraic |
| Example | |
| Translate into algebra. Let n = the number. | |
| Multiply. | |
| Solution | 37.8 is 45% of 84. |
b.
| Steps | Algebraic |
| Example | |
| Translate. Let n = the amount. | |
| Multiply. | |
| Divide both sides by 0.085 and simplify. | |
| Solution | 8.5% of $56 is $4.76 |
Now that we have a problem-solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.
Try it!
- The label on Audrey’s yogurt said that one serving provided 12 grams of protein, which is 24% of the recommended daily amount. What is the total recommended daily amount of protein?
Solution
| Steps | Algebraic |
| What are you asked to find? | What total amount of protein is recommended? |
| Choose a variable to represent it. | Let a = total amount of protein. |
| Write a sentence that gives the information to find it. |
|
| Translate into an equation. | |
| Solve. | |
| Check: Does this make sense? | Yes, 24% is about
|
| 12 is about |
|
| Write a complete sentence to answer the question. | The amount of protein that is recommended is 50g. |
2. Veronica is planning to make muffins from a mix. The package says each muffin will be 240 calories and 60 calories will be from fat. What percent of the total calories is from fat?
Solution
| Steps | Algebraic |
| What are you asked to find? | What percent of the total calories is fat? |
| Choose a variable to represent it. | Let p = percent of fat. |
| Write a sentence that gives the information to find it. |
|
| Translate the sentence into an equation. | |
| Multiply. | |
| Divide both sides by 240. | |
| Put in percent form. | |
| Check: does this make sense? |
Yes, 25% is one-fourth; 60 is one-fourth of 240. So, 25% makes sense. |
| Write a complete sentence to answer the question. | Of the total calories in each muffin, 25% is fat. |
When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate, usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount, we multiply the discount rate by the original price.
The price a retailer pays for an item is called the original cost. The retailer then adds a mark-up to the original cost to get the list price, the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.
The sale price should always be less than the original price.
The list price should always be more than the original cost.
Try it!
Liam’s art gallery bought a painting at an original cost of $750. Liam marked the price up 40%. Find a. the amount of mark-up and b. the list price of the painting.
Solution
a.
| Steps | Algebraic |
| Identify what you are asked to find and choose a variable to represent it. | What is the amount of mark-up? Let m = the amount of mark-up. |
| Write a sentence that gives the information to find it. |
|
| Translate into an equation. | |
| Solve the equation. | |
| Write a complete sentence. | The mark-up on the painting was $300. |
b.
| Steps | Algebraic |
| Identify what you are asked to find and choose a variable to represent it. | What is the list price? Let p = the list price. |
| Write a sentence that gives the information to find it. |
|
| Translate into an equation. | |
| Solve the equation. | |
| Check. | Is the list price more than the original cost? Is $1,050 more than $750? Yes. |
| Write a complete sentence. | The list price of the painting was $1,050. |
Solve Simple Interest Applications
Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.
The amount of money you initially deposit into a bank is called the principal, P, and the bank pays you interest, I. When you take out a loan, you pay interest on the amount you borrow, also called the principal.
In either case, the interest is computed as a certain percent of the principal, called the rate of interest, r. The rate of interest is usually expressed as a percent per year and is calculated by using the decimal equivalent of the percent. The variable t, (for time) represents the number of years the money is saved or borrowed.
Interest is calculated as simple interest or compound interest. Here we will use simple interest.
Simple Interest
If an amount of money, P, called the principal, is invested or borrowed for a period of t years at an annual interest rate r, the amount of interest, I, earned or paid is
| I = Prt,
Where |
I = interest |
| P = principal | |
| r = rate | |
| t = time |
Interest earned or paid according to this formula is called simple interest.
The formula we use to calculate interest is I = Prt. To use the formula, we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.
Try it!
Areli invested a principal of $950 in her bank account that earned simple interest at an interest rate of 3%. How much interest did she earn in five years?
Solution
I = ?
P = $950
r = 3%
t = 5 years
| Steps | Algebraic |
| Identify what you are asked to find and choose a variable to represent it. | What is the simple interest?
Let I = interest. |
| Write the formula. | I = Prt |
| Substitute in the given information. | I = (950)(0.03)(5) |
| Simplify. | I = 142.5 |
| Check. | Is $142.50 a reasonable amount of interest on $950?
Yes. |
| Write a complete sentence. | The interest is $142.50. |
There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.
Try it!
Hang borrowed $7,500 from her parents to pay her tuition. In five years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of simple interest?
Solution
I = $1500
P = $7500
r = ?
t = 5 years
| Steps | Algebraic |
| Identify what you are asked to find and choose a variable to represent it. | What is the rate of simple interest?
Let r = rate of interest. |
| Write the formula. | I = Prt |
| Substitute in the given information. | 1,500 = (7,500)r(5) |
| Multiply. | 1,500 = 37,500r |
| Divide. | 0.04 = r |
| Change to percent form. | 4% = r |
| Check. | I = Prt |
| 1,500 |
|
| 1,500 = 1,500✓ | |
| Write a complete sentence. | The rate of interest was 4%. |
In the next example, we are asked to find the principal—the amount borrowed.
Try it!
Sean’s new car loan statement said he would pay $4,866.25 in interest from a simple interest rate of 8.5% over five years. How much did he borrow to buy his new car?
Solution
I = 4,866.25
P = ?
r = 8.5%
t = 5years
| Steps | Algebraic |
| Identify what you are asked to find and choose a variable to represent it. | What is the amount borrowed (the principal)?
Let P = principal borrowed. |
| Write the formula. | I = Prt |
| Substitute in the given information. | 4,866.25 = P(0.085)(5) |
| Multiply. | 4,866.25 = 0.425P |
| Divide. | 11,450 = P |
| Check. | I = Prt |
| 4,866.25 |
|
| 4,866.25 = 4,866.25✓ | |
| Write a complete sentence. | The principal was $11,450. |
Geometry Applications
In this objective we will use some common geometry formulas. We will adapt our problem-solving strategy so that we can solve geometry applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve shapes of some sort, most people find it helpful to draw a figure and label it with the given information. We will include this in the first step of the problem-solving strategy for geometry applications.
When we solve geometry applications, we often have to use some of the properties of the figures. We will review those properties as needed.
The next example involves the area of a triangle. The area of a triangle is one-half the base times the height. We can write this as ![]() , where b = length of the base and h = height.
, where b = length of the base and h = height.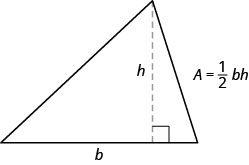
Try it!
The area of a triangular painting is 126 square inches. The base is 18 inches. What is the height?
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what you are looking for. | height of a triangle |
| 3. Name. Choose a variable to represent it. Draw the figure and label it with the given information. |
Let h = the height. |
| Area = 126 sq. in. | |
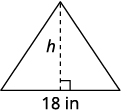 |
|
| 4. Translate. Write the appropriate formula. Substitute in the given information. |
|
| 5. Solve the equation. Divide both sides by 9. |
126 = 9h |
| 14 = h | |
| 6. Check. |
|
| 126=126✓ | |
| 7. Answer the question. | The height of the triangle is 14 inches. |
In the next example, we will work with a right triangle. To solve for the measure of each angle, we need to use two triangle properties. In any triangle, the sum of the measures of the angles is 180°. We can write this as a formula: m∠A + m ∠B + m ∠C=180. Also, since the triangle is a right triangle, we remember that a right triangle has one 90° angle.
Here, we will have to define one angle in terms of another. We will wait to draw the figure until we write expressions for all the angles we are looking for.
Try it!
The measure of one angle of a right triangle is 40 degrees more than the measure of the smallest angle. Find the measures of all three angles.
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what you are looking for. | the measures of all three angles |
| 3. Name. Choose a variable to represent it. |
Let a = 1st angle. |
| a + 40 = 2nd angle | |
| 90 = 3rd angle (the right angle) | |
| Draw the figure and label it with the given information. | 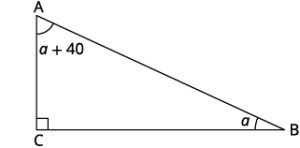 |
| 4. Translate. | |
| Write the appropriate formula. | m∠A + m∠B + m∠C = 180 |
| Substitute into the formula. | a (a + 40) + 90 = 180 |
| 5. Solve the equation. |
2a + 130 = 180 |
| 2a = 50 | |
| a = 25 first angle | |
| a + 40 second angle | |
| 25 + 40 | |
| 65 | |
| 90 third angle | |
| 6. Check. |
25 + 65 + 90 |
| 180 = 180✓ | |
| 7. Answer the question. | The three angles measure 25°, 65°, and 90°. |
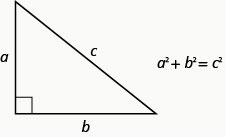
The next example uses another important geometry formula. The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. Writing the formula in every exercise and saying it aloud as you write it may help you memorize the Pythagorean Theorem.
In any right triangle, where a and b are the lengths of the legs, and c is the length of the hypotenuse, the sum of the squares of the lengths of the two legs equals the square of the length of the hypotenuse.
Try it!
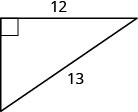
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what you are looking for. | the length of the leg of the triangle |
| 3. Name. | |
| Choose a variable to represent it. | Let a = the leg of the triangle. |
| Label side a. | 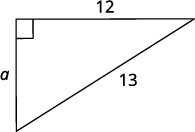 |
| 4. Translate. | NA |
| Write the appropriate formula. Substitute. |
a2 + b2 = c2 a2 + 122 = 132 |
| 5. Solve the equation. Isolate the variable term. Use the definition of square root. Simplify. |
a2 + 144 = 169 a2 = 25 a = √25 a = 5 |
| 6. Check. |
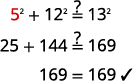 |
| 7. Answer the question. | The length of the leg is 5. |
The next example is about the perimeter of a rectangle. Since the perimeter is just the distance around the rectangle, we find the sum of the lengths of its four sides—the sum of two lengths and two widths. We can write is as P = 2L + 2W where L is the length and W is the width. To solve the example, we will need to define the length in terms of the width.
Try it!
The length of a rectangle is six centimeters more than twice the width. The perimeter is 96 centimeters. Find the length and width.
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what we are looking for. | the length and the width |
| 3. Name. Choose a variable to represent the width. The length is six more than twice the width. |
Let w = width. 2w + 6 = length 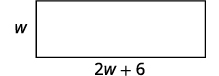 P = 96 cm |
| 4. Translate. | NA |
| Write the appropriate formula. | P = 2L + 2W |
| Substitute in the given information. | 96 = 2(2w + 6) + 2w |
| 5. Solve the equation. |
96 = 4w + 12 + 2w 96 = 6w + 12 84 = 6w 14 = W (width) Length: 2w + 6 2(14) + 6 34 = length |
6. Check. |
P = 2L + 2W 96 96 = 96✓ |
| 7. Answer the question. | The length is 34 cm and the width is 14 cm. |
The next example is about the perimeter of a triangle. Since the perimeter is just the distance around the triangle, we find the sum of the lengths of its three sides. We can write this as P = a + b + c, where a, b, and c are the lengths of the sides.
Try it!
- One side of a triangle is three inches more than the first side. The third side is two inches more than twice the first. The perimeter is 29 inches. Find the length of the three sides of the triangle.
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what we are looking for. | the lengths of the three sides of a triangle |
| 3. Name. Choose a variable to represent the length of the first side. |
Let x = length of 1st side. |
| x + 3 = length of 2nd side | |
2x + 2 = length of 3rd side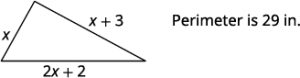 |
|
| 4. Translate. Write the appropriate formula. Substitute in the given information. |
P = a + b + c |
| 29 = x + (x + 3) + (2x + 2) | |
| 5. Solve the equation. |
29 = 4x + 5 |
| 24 = 4x | |
| 6 = x length of first side | |
| x + 3 length of second side | |
| 6 + 3 = 9 | |
| 2x + 2 length of third side | |
| 2 |
|
6. Check.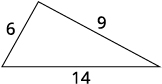 |
29 |
| 29 = 29✓ | |
| 7. Answer the question. | The lengths of the sides of the triangle are 6, 9, and 14 inches. |
2. The perimeter of a rectangular soccer field is 360 feet. The length is 40 feet more than the width. Find the length and width.
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what we are looking for. | the length and width of the soccer field |
| 3. Name. Choose a variable to represent it. The length is 40 feet more than the width. Draw the figure and label it with the given information. |
Let w = width. w + 40 = length 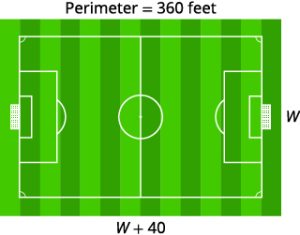 |
| 4. Translate. Write the appropriate formula and substitute. |
P = 2L + 2W |
| 360 = 2(w + 40) + 2w | |
| 5. Solve the equation. | 360 = 2w + 80 + 2w
360 = 4w + 80 280 = 4w 70 = w the width of the field w + 40 the length of the field 70 + 40 = 110 |
| 6. Check. |
P = 2L + 2W 360 360 = 360✓ |
| 7. Answer the question. | The length of the soccer field is 110 feet and the width is 70 feet. |
Applications of these geometric properties can be found in many everyday situations as shown in the next example.
Try it!
Kelvin is building a gazebo and wants to brace each corner by placing a 10” piece of wood diagonally as shown.
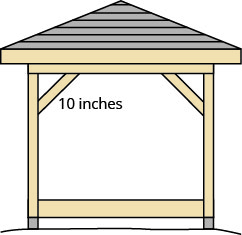 How far from the corner should he fasten the wood if he wants the distances from the corner to be equal? Approximate to the nearest tenth of an inch.
How far from the corner should he fasten the wood if he wants the distances from the corner to be equal? Approximate to the nearest tenth of an inch.
Solution
| Steps | Algebraic |
| 1. Read the problem. | NA |
| 2. Identify what we are looking for. | the distance from the corner that the bracket should be attached |
| 3. Name. Choose a variable to represent it.
Draw the figure and label it with the given information. |
Let x = the distance from the corner.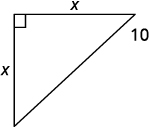 |
| 4. Translate. Write the appropriate formula and substitute. |
a2 + b2 = c2
x2 + x2 = 102 |
| 5. Solve the equation. Isolate the variable. Use the definition of square root. Simplify. Approximate to the nearest tenth. |
2x2 = 100
x2 = 50 x = √50 x ≈ 7.1 |
| 6. Check. |
a2 + b2 = c2
(7.1)2 + (7.1)2 ≈ 102 Yes. |
| 7. Answer the question. | Kelvin should fasten each piece of wood approximately 7.1” from the corner. |
Access this online resource for additional instruction and practice with solving for a variable in literal equations.
Solve Formulas for One Variable
We have all probably worked with some geometric formulas in our study of mathematics. Formulas are used in so many fields, it is important to recognize formulas and be able to manipulate them easily.
It is often helpful to solve a formula for a specific variable. If you need to put a formula in a spreadsheet, it is not unusual to have to solve it for a specific variable first. We isolate that variable on one side of the equals sign with a coefficient of one and all other variables and constants are on the other side of the equal sign.
Geometric formulas often need to be solved for another variable, too. The formula ![]() is used to find the volume of a right circular cone when given the radius of the base and height. In the next example, we will solve this formula for the height.
is used to find the volume of a right circular cone when given the radius of the base and height. In the next example, we will solve this formula for the height.
Try it!
Solve the formula V = ![]() πr2h for h.
πr2h for h.
Solution
| Steps | Algebraic |
| Write the formula. | |
| Remove the fraction on the right. | 3 • V= 3• |
| Simplify. | 3V = πr2h |
| Divide both sides by πr2. |
We could now use this formula to find the height of a right circular cone when we know the volume and the radius of the base, by using the formula h = ![]() .
.
In the sciences, we often need to change temperature from Fahrenheit to Celsius or vice versa. If you travel in a foreign country, you may want to change the Celsius temperature to the more familiar Fahrenheit temperature.
Try it!
Solve the formula ![]() for F.
for F.
Solution
| Steps | Algebraic |
| Write the formula. | |
| Remove the fraction on the right. | |
| Simplify. | |
| Add 32 to both sides. |
We can now use the formula ![]() to find the Fahrenheit temperature when we know the Celsius temperature.
to find the Fahrenheit temperature when we know the Celsius temperature.
The next example uses the formula for the surface area of a right cylinder.
Try it!
Solve the formula S = 2πr2 + 2πrh for h.
Solution
| Steps | Algebraic |
| Write the formula. | S = 2πr2 + 2πrh |
| Isolate the h term by subtracting 2πr2 from each side. | S – 2πr2 = 2πr2 – 2πr2 + 2πrh |
| Simplify. | S – 2πr2 = 2πrh |
| Solve for h by dividing both sides by 2πr. | |
| Simplify. |
Key Concepts
- How To Use a Problem-Solving Strategy for Word Problems
- Read the problem. Make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using proper algebra techniques.
- Check the answer in the problem to make sure it makes sense.
- Answer the question with a complete sentence.
- How To Find Percent Change
- Find the amount of change
change = new amount − original amount - Find what percent the amount of change is of the original amount.
change is what percent of the original amount?
- Find the amount of change
- Discount
amount of discount = discount rate original price
original price
sale price = original amount − discount
- Mark-up
amount of mark-up = mark-up rate original cost
original cost
list price = original cost + mark up
- Simple Interest
If an amount of money, P, called the principal, is invested or borrowed for a period of t years at an annual interest rate r, the amount of interest, I, earned or paid is:
| I = interest | |
| I = Prt where | P = principal |
| r = rate | |
| t = time |

