"

23 Factoring Polynomials

Greatest Common Factor of a Polynomial

We have learned how to factor numbers to find the least common multiple (LCM) of two or more numbers. Now we will factor expressions and find the greatest common factor of two or more expressions. The method we use is similar to what we used to find the LCM.

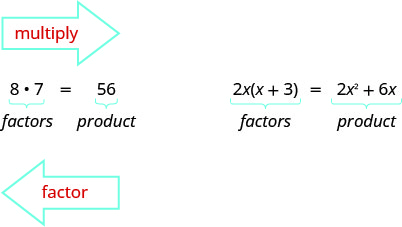
8 times 7 is 56. Here 8 and 7 are factors and 56 is the product. An arrow pointing from 8 times 7 to 56 is labeled multiply. An arrow pointing from 56 to 8 times 7 is labeled factor. 2x open parentheses x plus 3 close parentheses equals 2x squared plus 6x. Here the left side of the equation is labeled factors and the right side is labeled products.

Greatest Common Factor

The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.

 

Try it!

Find the greatest common factor of  21x3, 9x2, 15x.

Steps Algebraic
Factor each coefficient into primes and write the variables with exponents in expanded form.
Circle the common factors in each column.
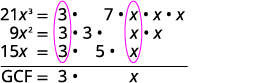Bring down the common factors.		 The terms are 21 x cubed, 9 x squared and 15 x. The first step is to factor each coefficient into primes and write the variables with exponents in expanded form. 21 x cubed is written as 3 times 7 times x times x times x. 9 x squared is written as 3 times 3 times x times x. 15 x is written as 3 times 5 times x. Now bring down the common factors. So, GCF is 3 times x. Now multiply the factors. So, GCF of 21 x cubed, 9 x squared and 15x is 3x.
Multiply the factors. The GCF of 21x3, 9x2 and 15x is 3x.

When we study fractions, we learn that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance, 4 is the GCF of 16 and 20 because it is the largest number that divides evenly into both 16 and 20. The GCF of polynomials works the same way:  4x is the GCF of 16x and 20x2 because it is the largest polynomial that divides evenly into both 16x and 20x2.

When factoring a polynomial expression, our first step should be to check for a GCF. Look for the GCF of the coefficients, and then look for the GCF of the variables.

Greatest Common Factor

The greatest common factor (GCF) of polynomials is the largest polynomial that divides evenly into the polynomials.

Given a polynomial expression, factor out the greatest common factor.

  1. Identify the GCF of the coefficients.
  2. Identify the GCF of the variables.
  3. Combine to find the GCF of the expression.
  4. Determine what the GCF needs to be multiplied by to obtain each term in the expression.
  5. Write the factored expression as the product of the GCF and the sum of the terms we need to multiply by.

We state the Distributive Property here just as you saw it in earlier chapters and “in reverse.”

Distributive Property

If a, b, and c are real numbers, then

a(b + c) = ab + ac and ab + ac = a(b + c)

The form on the left is used to multiply. The form on the right is used to factor.

So how do you use the Distributive Property to factor a polynomial? You just find the GCF of all the terms and write the polynomial as a product!

Try it! – How to Use the Distributive Property to factor a polynomial

Factor:  8m3 − 12m2n + 20mn2.
Solution

Step 1 is find the GCF of all the terms in the polynomial. GCF of 8 m cubed, 12 m squared n and 20 mn squared is 4m.
Step 1 is find the GCF of all the terms in the polynomial. GCF of 8 m cubed, 12 m squared n and 20 mn squared is 4m.
In step 3, use the reverse Distributive Property to factor the expression as 4m open parentheses 2 m squared minus 3 mn plus 5 n squared close parentheses.
Step 4 is to check by multiplying the factors. By multiplying the factors, we get the original polynomial.

Try it! – Factoring the Greatest Common Factor

Factor:  6x3y3 + 45x2y2 + 21xy.

Solution

Steps Algebraic
First, find the GCF of the expression. (Note that the GCF of a set of expressions in the form xn will always be the exponent of lowest degree.)  The GCF of 6, 45 and 21 is 3.

The GCF of x3, x2, and x is x.

And the GCF of y3, y2, and y is y.
Combine these to find the GCF of the polynomial, GCF = 3xy
Next, determine what the GCF needs to be multiplied by to obtain each term of the polynomial. We find that 3xy(2x2y2) = 6x3y3, 3xy(15xy) = 45x2y2, and 3xy(7) = 21xy.
Finally, write the factored expression as the product of the GCF and the sum of the terms we needed to multiply by. (3xy)(2x2y2 + 15xy + 7)

 

Analysis

After factoring, we can check our work by multiplying. Use the distributive property to confirm that (3xy)(2x2y2 + 15xy + 7) = 6x3y3 + 45x2y2 + 21xy.

Try it!

Factor x(b2 – a) + 6(b2 – a) by pulling out the GCF.

Solution

(b2 – a)(x + 6)

Factor by Grouping

Sometimes there is no common factor of all the terms of a polynomial. When there are four terms we separate the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts. Not all polynomials can be factored. Just like some numbers are prime, some polynomials are prime.

Try it! – How to Factor a Polynomial by Grouping

Factor by grouping:  xy + 3y + 2x + 6.
Solution

Step 1 is to group the terms with common factors. There is no greatest common factor in all the four terms of xy plus 3y plus 2x plus 6. So, separate the first two terms from the second two.
Step 2 is to factor out the common factor in each group. By factoring the GCF from the first 2 terms, we get y open parentheses x plus 3 close parentheses plus 2x plus 6. Factoring the GCF from the second 2 terms, we get y open parentheses x plus 3 close parentheses plus 2 open parentheses x plus 3 close parentheses.
Step 3 is to factor the common factor from the expression. Notice that each term has a common factor of x plus 3. By factoring this out, we get open parentheses x plus 3 close parentheses open parentheses y plus 2 close parentheses
Step 4 is to check by multiplying the expressions to get the result xy plus 3y plus 2x plus 6.
Factor by grouping.
  1. Group terms with common factors.
  2. Factor out the common factor in each group.
  3. Factor the common factor from the expression.
  4. Check by multiplying the factors.

Try it! 

Factor by grouping:  a. x2 + 3x − 2x − 6    b.  6x2 − 3x − 4x + 2.

Solution

a.

Steps Algebraic
First, find the GCF of the expression. (Note that the GCF of a set of expressions in the form xn will always be the exponent of lowest degree.) There is no GCF in all four terms.
Separate into two parts.    x2 + 3x ,   −2x − 6
Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms.      x(x + 3) − 2(x + 3)
Factor out the common factor.                     (x + 3)(x − 2)

Check on your own by multiplying.

b.

Steps Algebraic
First, find the GCF of the expression. (Note that the GCF of a set of expressions in the form xn will always be the exponent of lowest degree.) There is no GCF in all four terms.
Separate into two parts.         6x2 − 3x   −4x + 2
Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms.     3x(2x − 1) −2(2x − 1)
Factor out the common factor.   (2x − 1)(3x − 2)

Check on your own by multiplying.

Factor Trinomials

Does the order of the factors matter?

No. Multiplication is commutative, so the order of the factors does not matter.

You have already learned how to multiply binomials using FOIL. Now you’ll need to “undo” this multiplication. To factor the trinomial means to start with the product, and end with the factors.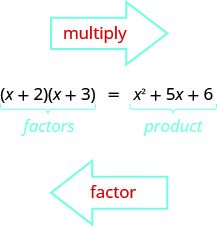Figure shows the equation open parentheses x plus 2 close parentheses open parentheses x plus 3 close parentheses equals x squared plus 5 x plus 6. The left side of the equation is labeled factors and the right is labeled product. An arrow pointing right is labeled multiply. An arrow pointing left is labeled factor.To figure out how we would factor a trinomial of the form x2 + bx + c, such as x2 + 5x + 6 and factor it to (x + 2)(x + 3), let’s start with two general binomials of the form (x + m) and (x + n).

Steps Algebraic
Example We have open parentheses x plus m close parentheses open parentheses x plus n close parentheses.
Foil to find the product. Foil to find the product x squared plus mx plus nx plus mn.
Factor the GCF from the middle terms. Factor the GCF from the middle terms x squared plus open parentheses m plus n close parentheses x plus mn.
Our trinomial is of the form x2 + bx + c. Now our trinomial is of the form x squared plus bx plus c, where b is m plus n and c is mn

This tells us that to factor a trinomial of the form x2 + bx + c, we need two factors (x + m) and (x + n) where the two numbers m and n multiply to c and add to b.

Try i1! – How to Factor a Trinomial of the form x2+bx+c

Factor:  x2 + 11x + 24.

Solution


Step 1 is to write the factors of x squared plus 11x plus 24 as two binomials with first terms x. Write two sets of parentheses and put x as the first term.
Step 2 is to find two numbers m and n that multiply to c, m times n is c and add to b, m plus n is b. So, find two numbers that multiply to 24 and add to 11. Factors of 24 are 1 and 24, 2 and 12, 3 and 8, 4 and 6. Sum of factors: 1 plus 24 is 25, 2 plus 12 is 14, 3 plus 8 is 11 and 4 plus 6 is 10.
Step 3 is to use m and n, in this case, 3 and 8, as the last terms of the binomials. So we get open parentheses x plus 3 close parentheses open parentheses x plus 8 close parentheses
Step 4 is to check by multiplying the factors to get the original polynomial.

Let’s summarize the method we just developed to factor trinomials of the form x2 + bx + c.

Strategy for Factoring Trinomials of the Form x2 + bx + c

When we factor a trinomial, we look at the signs of its terms first to determine the signs of the binomial factors.

x2 + bx + c
(x + m)(x + n)
When c is positive, m and n have the same sign.
b positive                                                                                               b negative
m,n positive                                                                                        m,n negative
x2 + 5x + 6                                                                                                   x2 − 6x + 8
(x + 2)(x + 3)                                                                                                 (x − 4)(x − 2)
same signs                                                                                             same signs
When c is negative, m and n have opposite signs.
x2 + x − 12                                                                                                  x2 − 2x − 15
(x + 4)(x − 3)                                                                                                (x − 5)(x + 3)
opposite signs                                                                                     opposite signs

Notice that, in the case when m and n have opposite signs, the sign of the one with the larger absolute value matches the sign of b.

What happens when the leading coefficient is not 1 and there is no GCF? There are several methods that can be used to factor these trinomials. First we will use the Trial and Error method.

Let’s factor the trinomial 3×2 + 5x + 2.

From our earlier work, we expect this will factor into two binomials.

3x2 + 5x + 2

(____)(____)

We know the first terms of the binomial factors will multiply to give us 3x2. The only factors of 3x2 are 1x, 3x. We can place them in the binomials.


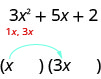he polynomial is 3x squared plus 5x plus 2. There are two pairs of parentheses, with the first terms in them being x and 3x.Check: Does 1x · 3x = 3x2?

We know the last terms of the binomials will multiply to 2. Since this trinomial has all positive terms, we only need to consider positive factors. The only factors of 2 are 1, 2. But we now have two cases to consider as it will make a difference if we write 1, 2 or 2, 1.


Figure shows the polynomial 3x squared plus 5x plus 2 and two possible pairs of factors. One is open parentheses x plus 1 close parentheses open parentheses 3x plus 2 close parentheses. The other is open parentheses x plus 2 close parentheses open parentheses 3x plus 1 close parentheses.Which factors are correct? To decide that, we multiply the inner and outer terms.


Figure shows the polynomial 3x squared plus 5x plus 2 and two possible pairs of factors. One is open parentheses x plus 1 close parentheses open parentheses 3x plus 2 close parentheses. The other is open parentheses x plus 2 close parentheses open parentheses 3x plus 1 close parentheses. In each case, arrows are shown pairing the first term of the first factor with the last term of the second factor and the first term of the second factor with the last term of the first factor.Since the middle term of the trinomial is 5x, the factors in the first case will work. Let’s use FOIL to check.

(x + 1)(3x + 2)
3x2 + 2x + 3x + 2
3x2 + 5x + 2 ✓

Our result of the factoring is:

3x2 + 5x + 2
(x + 1)(3x + 2)

Try it! – How to Factor a Trinomial Using Trial and Error

Factor completely using trial and error:  3y2 + 22y + 7.

Solution


Step 1 is to write the trinomial in descending order. The trinomial 3 y squared plus 22y plus 7 is already in descending order.
Step 2 is to factor the GCF. Here, there is none.
Step 3 is Find all the factor pairs of the first term. The only factors here are 1y and 3y. Since there is only one pair, we can put each as the first term in the parentheses.
Step 4 is to find all the factor pairs of the third term. Here, the only pair is 1 and 7.
Step 5 is to test all the possible combinations of the factors until the correct product is found. For possible factors open parentheses y plus 1 close parentheses open parentheses 37 plus 7 close parentheses, the product is 3 y squared plus 10y plus 7. For the possible factors open parentheses y plus 7 close parentheses open parentheses 3y plus 1 close parentheses, the product is 3 y squared plus 22y plus 7, which is the correct product. Hence, the correct factors are open parentheses y plus 7 close parentheses open parentheses 3y plus 1 close parentheses.
Step 6 is to check by multiplying.

Factor trinomials of the form ax2 + bx + c using trial and error.

  1. Write the trinomial in descending order of degrees as needed.
  2. Factor any GCF.
  3. Find all the factor pairs of the first term.
  4. Find all the factor pairs of the third term.
  5. Test all the possible combinations of the factors until the correct product is found.
  6. Check by multiplying.

Remember, when the middle term is negative and the last term is positive, the signs in the binomials must both be negative.

Try it!

Factor completely using trial and error:  6b2 − 13b + 5.

Solution

Steps Algebraic
The trinomial is already in descending order. The trinomial 6 b squared minus 13 b plus 5 is already in descending order.
Find the factors of the first term. Factoring the first term, we get 1b times 6b and 2b times 3b, which are displayed in red font below the 6b.
Find the factors of the last term. Consider the signs.
Since the last term, 5, is positive its factors must both be
positive or both be negative. The coefficient of the
middle term is negative, so we use the negative factors.		 To find the factors of the last term, consider the signs. Since the last term, 5, is positive its factors must both be positive or both be negative. The coefficient of the middle term is negative, so we use the negative factors minus 1 and minus 5, shown below the 6 in red.

Consider all the combinations of factors.

Example
6b2 − 13b + 5
Possible factors Product
(b − 1)(6b − 5) 6b2 − 11b + 5
(b − 5)(6b − 1) 6b2 − 31b + 5
(2b − 1)(3b − 5) 6b2 − 13b + 5*
(2b − 5)(3b − 1) 6b2 − 17b + 5

The correct factors are those whose product is the original trinomial.               (2b − 1)(3b − 5)

Check by multiplying:

(2b − 1)(3b − 5)

6b2 − 10b − 3b + 5

6b2 − 13b + 5 ✓

When we factor an expression, we always look for a greatest common factor first. If the expression does not have a greatest common factor, there cannot be one in its factors either. This may help us eliminate some of the possible factor combinations.

Try it!

Factor completely using trial and error:   18x2 − 37xy + 15y2.

Solution

Steps Algebraic
The trinomial is already in descending order. The trinomial 18 x squared minus 37xy plus 15y squared is already in descending order.
Find the factors of the first term. 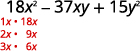Factoring the first term, we get 1x times 18x, 2x times 9x and 3x times 6x. These are displayed below the 18x in red.
Find the factors of the last term. Consider the signs.
Since 15 is positive and the coefficient of the middle
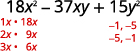term is negative, we use the negative factors.		 To find the factors of the last term, consider the signs. Since 15 is positive and the coefficient of the middle term is negative, we use the negative factors minus 1, minus 5 and minus 5, minus 1. These are displayed below the 15y in red.

Consider all the combinations of factors.

This table shows the possible factors and corresponding products of the trinomial 18 x squared minus 37xy plus 15 y squared. In some pairs of factors, when one factor contains two terms with a common factor, that factor is highlighted. In such cases, product is not an option because if trinomial has no common factors, then neither factor can contain a common factor. Factor: open parentheses x minus 1y close parentheses open parentheses 18x minus 15y close parentheses, highlighted. Factor, open parentheses x minus 15y close parentheses open parentheses 18x minus 1y close parentheses; product: 18 x squared minus 271xy plus 15 y squared. Factor open parentheses x minus 3y close parentheses open parentheses 18x minus 5 y close parentheses; product: 18 x squared minus 59xy plus 15 y squared. Factor: open parentheses x minus 5y close parentheses open parentheses 18x minus 3y close parentheses highlighted. Factor: open parentheses 2x minus 1y close parentheses open parentheses 9x minus 15y close parentheses highlighted. Factor: open parentheses 2x minus 15y close parentheses open parentheses 9x minus 1y close parentheses; product 18 x squared minus 137 xy plus 15y squared. Factor: open parentheses 2x minus 3y close parentheses open parentheses 9x minus 5y close parentheses; product: 18 x squared minus 37xy plus 15 y squared, which is the original trinomial. Factor: open parentheses 2x minus 57 close parentheses open parentheses 9x minus 3y close parentheses highlighted. Factor: open parentheses 3x minus 1y close parentheses open parentheses 6x minus 15y close parentheses highlighted. Factor: open parentheses 3x minus 15y close parentheses highlighted open parentheses 6x minus 1y close parentheses. Factor: open parentheses 3x minus 3y close parentheses highlighted open parentheses 6x minus 5y.

The correct factors are those whose product is the original trinomial.

     (2x − 3y)(9x − 5y)

Check by multiplying:

(2x − 3y)(9x − 5y)

18x2 − 10xy − 27xy + 15y2

18x2 − 37xy + 15y2

Don’t forget to look for a GCF first and remember if the leading coefficient is negative, so is the GCF.

Try it!

Factor completely using trial and error:  −10y4 − 55y3 − 60y2.

Solution

Steps Algebraic
Example The trinomial is minus 10 y to the power 4 minus 55 y cubed minus 60 y squared.
Notice the greatest common factor, so factor it first. Factoring the GCF, we get minus 5 y squared open parentheses 2 y squared plus 11y plus 12 close parentheses.
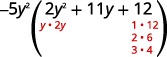Factor the trinomial. The factors of the first term of the trinomial in the parentheses are y and 2y, shown below the 2y in red. The factor pairs of the last term are 1 and 12, 2 and 6, 3 and 4, shown below the 12 in red.

Consider all the combinations.

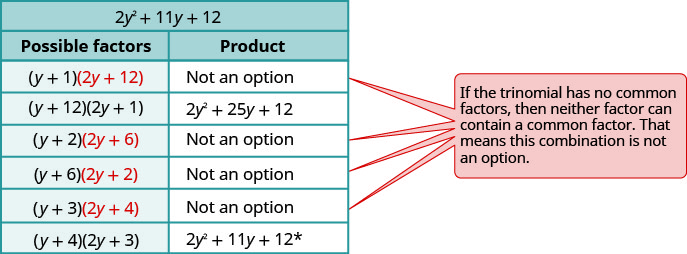
This table shows the possible factors and product of the trinomial 2 y squared plus 11y plus 12. In some pairs of factors, when one factor contains two terms with a common factor, that factor is highlighted. In such cases, product is not an option because if trinomial has no common factors, then neither factor can contain a common factor. Factor: y plus 1, 2y plus 12 highlighted. Factor: y plus 12, 2y plus 1; product: 2 y squared plus 25y plus 12. Factor: y plus 2, 2y plus 6 highlighted. Factor: y plus 6, 2y plus 2 highlighted. Factor: y plus 3, 2y plus 4 highlighted. Factor: y plus 4, 2y plus 3; product: 2 y squared plus 11y plus 12. This is the original trinomial.

The correct factors are those whose product is the original trinomial. Remember to include the factor −5y2.

 −5y2(y + 4)(2y + 3)

Check by multiplying:

−5y2(y + 4)(2y + 3)

−5y2(2y2 + 8y + 3y + 12)

−10y4 − 55y3 − 60y2 ✓

Factor Difference of Squares

Do you remember the Difference of Squares from the last module? A difference of squares is a perfect square subtracted from a perfect square. Recall that a difference of squares can be rewritten as factors containing the same terms but opposite signs because the middle terms cancel each other out when the two factors are multiplied.

Differences of Squares

A difference of squares can be rewritten as two factors containing the same terms but opposite signs.

a2 − b2 = (a + b)(a − b)

Step 1. Does the binomial fit the pattern?                                                                                                                                            a2 − b2

Is this a difference?                                                                                                                                                                          ____−____

Are the first and last terms perfect squares?

Step 2. Write them as squares.                                                                                                                                                             (a)2 − (b)2

Step 3. Write the product of conjugates.                                                                                                                                          (a − b)(a + b)

Step 4. Check by multiplying.

Try it!

Factor:  144x2 − 49y2.

Solution

Steps Algebraic
Example 144x2 − 49y2
Is this a difference of squares? Yes.         (12x)2 − (7y)2
Factor as the product of conjugates.   (12x − 7y)(12x + 7y)
Check by multiplying. (12x − 7y)(12x + 7y)

144x2 − 49y2 ✓

Try it! – Factoring a Difference of Squares

Factor  9x2 − 25.

Solution

Notice that 9x2 and 25 are perfect squares because 9x2 = (3x)2 and 25 = 52. The polynomial represents a difference of squares and can be rewritten as (3x  +5)(3x − 5).

As always, you should look for a common factor first whenever you have an expression to factor. Sometimes a common factor may “disguise” the difference of squares and you won’t recognize the perfect squares until you factor the GCF.

Try it!

Factor:  48x4y2 − 243y2.

Solution

Steps Algebraic
Example 48x4y2 − 243y2
Is there a GCF?  Yes, 3y2—factor it out!             3y2(16x4 − 81)
Is the binomial a difference of squares? Yes.            3y2((4x2)2 − (9)2)
Factor as a product of conjugates.   3y2(4x2 − 9)(4x2 + 9)
Notice the first binomial is also a difference of squares!        3y2((2x)2 − (3)2)(4x2 + 9)
Factor it as the product of conjugates.  The last factor, the sum of squares, cannot be factored.    3y2(2x − 3)(2x + 3)(4x2 + 9)
Check by multiplying: 3y2(2x − 3)(2x + 3)(4x2 + 9)

3y2(4x2 − 9)(4x2 + 9)

3y2(16x4 − 81)

48x4y2 − 243y2✓

Factoring a Perfect Square Trinomial

Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter.


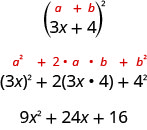
In open parentheses 3x plus 4 close parentheses squared, 3x is a and 4 is b. Writing it as a squared plus 2ab plus b squared, we get open parentheses 3x close parentheses squared plus 2 times 3x times 4 plus 4 squared. This is equal to 9 x squared plus 24x plus 16.

Perfect Square Trinomials

a2 + 2ab + b2 = (a + b)2

and

a2 − 2ab + b2 = (a − b)2

We can use this equation to factor any perfect square trinomial.

Step 1. Does the trinomial fit the pattern?                                                                                                                       a2 + 2ab + b2                             a2 – 2ab + b2   

Is the first term a perfect square?                                                                                                                                           (a)2                                           (b)2

Write it as a square.

Is the last term a perfect square?                                                                                                                                (a)2                 (b)2                     (a)2                (b)2   

Write it as a square.

Check the middle term. Is it 2ab?                                                                                                                               (a)2   ↘2 · a · b↙   (b)2                      (a)2   ↘2 · a · b↙   (b)2

Step 2. Write the square of the binomial.                                                                                                                            (a + b)2                                        (a − b)2

Step 3. Check by multiplying.

Try it!

Factor:  9×2 + 12x + 4.

Solution


Step 1 is to check if the trinomial fits the perfect square trinomials pattern, a squared plus 2ab plus b squared. For this we check if the first term is a perfect square. 9 x squared is the square of 3x. Next we check if the last term is a perfect square. 4 is the square of 2. Next we check if the middle term is 2ab. 12 x is twice 3x times 2. Hence we have a perfect square trinomial.
Step 2 is to write this as the square of a binomial. We write it as open parentheses 3x plus 2 close parentheses squared.
Step 3 is to check by multiplying.

Try it! – Factoring a Perfect Square Trinomial

Factor:  25x2 + 20x + 4.

Solution

Notice that 25x2 and 4 are perfect squares because 25x2 = (5x)2 and 4 = 22. Then check to see if the middle term is twice the product of 5x and 2. The middle term is, indeed, twice the product: 2(5x)(2) = 20x. Therefore, the trinomial is a perfect square trinomial and can be written as (5x+2)2.

Try it!

Factor:  81y2 − 72y + 16.

Solution

The first and last terms are squares. See if the middle term fits the pattern of a perfect square trinomial. The middle term is negative, so the binomial square would be (a − b)2.

Steps Algebraic
Example The trinomial is 81 y squared minus 72y plus 16.
Are the first and last terms perfect squares? The first and last terms are perfect squares of 9y and 4.
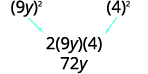Check the middle term. Check the middle term. Shown by arrows pointing down from the perfect squares of 9y and 4. It is twice 9y times 4.
Does it match (a−b)2? Yes. The trinomial matches a minus b the whole squared. shown with a squared above 9y, minus 2 over the minus 2, a over the 2nd 9y, b over the next 4, and b squared over the last 4.
Write as the square of a binomial. So we write it as the square of a binomial open parentheses 9y minus 4 close parentheses squared. Finally, we check by multiplying.
Check by multiplying:

 (9y − 4)2(9y)2 − 2 · 9y · 4 + 42

81y2 − 72y + 16 ✓

Factoring the Sum and Difference of Cubes

Now, we will look at two new special products: the sum and difference of cubes. Although the sum of squares cannot be factored, the sum of cubes can be factored into a binomial and a trinomial.

We can use the acronym SOAP to remember the signs when factoring the sum or difference of cubes. The first letter of each word relates to the signs: Same Opposite Always Positive. For example, consider the following example.

x3 − 23 = (x − 2)(x2 + 2x + 4)

The sign of the first 2 is the same as the sign between x3 − 23. The sign of the 2x term is opposite the sign between x3 − 23. And the sign of the last term, 4, is always positive.

Sum and Difference of Cubes

We can factor the sum of two cubes as

a3 + b3 = (a + b)(a2 − ab + b2)

We can factor the difference of two cubes as

a3 − b3 = (a − b)(a2 + ab + b2)

We’ll check the first pattern and leave the second to you.

Steps Algebraic
Example Open parentheses a plus b close parentheses open parentheses a squared minus ab plus b squared.
Distribute. Distribute: a open parentheses a squared minus ab plus b squared plus b open parentheses a squared minus ab plus b squared close parentheses.
Multiply. Multiply: a cubed minus a squared b plus ab squared plus a squared b minus ab squared plus b cubed.
Combine like terms. Combine like terms: a cubed plus b cubed.

Given a sum of cubes or difference of cubes, factor it.

  1. Confirm that the first and last term are cubes,
    a3 + b3 or a3 − b3.
  2. For a sum of cubes, write the factored form as
    (a + b)(a2 − ab + b2). For a difference of cubes, write the factored form as (a − b)(a2 + ab + b2).

Try it!

Factor:  x3 + 64.

Solution


Step 1 is to check if the binomial fits the sum or difference of cubes pattern. For this, we check whether it is a sum or difference. x cubed plus 64 is a sum. Next we check if the first and last terms are perfect cubes. They are
Step 2 is to rewrite as cubes. So we rewrite as x cubed plus 4 cubed.
Step 3 is to use either the sum or difference of cubes pattern. Since this is a sum of cubes, we get open parentheses x plus 4 close parentheses open parentheses x squared minus 4x plus 4 squared.
Step 4 is to simplify inside the parentheses. It is already simplified
Step 5 is to check by multiplying the factors.

Try it! – Factoring a Difference of Cubes

Factor: 8x3 − 125.

Solution

Notice that 8x3 and 125 are cubes because 8x3 = (2x)3 and 125 = 53. Write the difference of cubes as (2x − 5)(4x2 + 10x + 25).

Analysis

Just as with the sum of cubes, we will not be able to further factor the trinomial portion.

General Strategy to Factor Polynomials

You have now become acquainted with all the methods of factoring that you will need in this course. The following chart summarizes all the factoring methods we have covered, and outlines a strategy you should use when factoring polynomials.

This chart shows the general strategies for factoring polynomials. It shows ways to find GCF of binomials, trinomials and polynomials with more than 3 terms. For binomials, we have difference of squares: a squared minus b squared equals a minus b, a plus b; sum of squares do not factor; sub of cubes: a cubed plus b cubed equals open parentheses a plus b close parentheses open parentheses a squared minus ab plus b squared close parentheses; difference of cubes: a cubed minus b cubed equals open parentheses a minus b close parentheses open parentheses a squared plus ab plus b squared close parentheses. For trinomials, we have x squared plus bx plus c where we put x as a term in each factor and we have a squared plus bx plus c. Here, if a and c are squares, we have a plus b whole squared equals a squared plus 2 ab plus b squared and a minus b whole squared equals a squared minus 2 ab plus b squared. If a and c are not squares, we use the ac method. For polynomials with more than 3 terms, we use grouping.
General Strategy for Factoring Polynomials

Use a general strategy for factoring polynomials.

  1. Is there a greatest common factor?
    Factor it out.
  2. Is the polynomial a binomial, trinomial, or are there more than three terms?
    If it is a binomial:

    • Is it a sum?
      Of squares? Sums of squares do not factor.
      Of cubes? Use the sum of cubes pattern.
    • Is it a difference?
      Of squares? Factor as the Difference of Squares.
      Of cubes? Use the difference of cubes pattern.
    • Is it of the form
      x2 + bx + c? Undo FOIL.
    • Is it of the form
      ax2 + bx + c?
      If a and c are squares, check if it fits the trinomial square pattern.
      Use the trial and error or “ac” method.

    If it has more than three terms:

    • Use the grouping method.
  3. Check.
    Is it factored completely?
    Do the factors multiply back to the original polynomial?

Remember, a polynomial is completely factored if, other than monomials, its factors are prime!

 

Try it

Factor completely: 7x3 − 21x2 − 70x.

Solution

Steps Algebraic
Example 7x3 − 21x2 − 70x
Is there a GCF? Yes, 7x. Factor out the GCF.                          7x(x2 − 3x − 10)
In the parentheses, is it a binomial, trinomial, or are there more terms? Trinomial with leading coefficient 1.
“Undo” FOIL.   7x(x    )(x    ) = 7x(x + 2)(x − 5)
Is the expression factored completely? Yes. Neither binomial can be factored.
Check by multiplying: 7x(x + 2)(x − 5)

7x(x2 − 5x + 2x − 10)

7x(x2 − 3x − 10)

7x3 − 21x2 − 70x ✓

Try it!

Factor completely:  24y2 − 150.

Solution

Steps Algebraic
Example 24y2 − 150
Is there a GCF?  Yes, 6—factor it out!      6(4y2 − 25)
In the parentheses, is it a binomial, trinomial or are there more than three terms? Binomial.
Is it a sum? No.
Is it a difference? Of squares or cubes? Yes, squares. 6((2y)2 − (5)2)
Write as a product of conjugates.      6(2y − 5)(2y + 5)
Is the expression factored completely? Neither binomial can be factored.
Check by multiplying: 6(2y − 5)(2y + 5)

6(4y2 − 25)

24y2 − 150 ✓

The next example can be factored using several methods. Recognizing the trinomial squares pattern will make your work easier.

Try it!

Factor completely:  4a2 − 12ab + 9b2.

Solution

Steps Algebraic
Example 4a2 − 12ab + 9b2
Is there a GCF? No.
Is it a binomial, trinomial, or are there more terms?  Trinomial with a≠1. But the first term is a perfect square.
Is the last term a perfect square? Yes.         (2a)2 − 12ab + (3b)2
Does it fit the pattern,a2−2ab+b2? Yes.    Write it as a square.         (2a)2  ↘ − 12ab + − 2(2a)(3b) ↙  (3b)2
Is the expression factored completely? Yes.
Check by multiplying: (2a − 3b)2

(2a)2 − 2 · 2a · 3b + (3b)2

4a2 − 12ab + 9b2 ✓

When we have factored a polynomial with four terms, most often we separated it into two groups of two terms. Remember that we can also separate it into a trinomial and then one term.

Try it!

Factor completely:  9x2 − 12xy + 4y2 − 49.

Solution

Steps Algebraic
Example 9x2 − 12xy + 4y2 − 49
Is there a GCF? .       No
With more than 3 terms, use grouping. Last 2 terms have no GCF. Try grouping first 3 terms.     9x2 − 12xy + 4y2 − 49
Factor the trinomial with a ≠ 1. But the first term is a perfect square.
Is the last term of the trinomial a perfect square? Yes.     (3x)2−12xy+(2y)2−49
Does the trinomial fit the pattern, a2 − 2ab + b2?Yes.         (3x)2 ↘ −12xy + −2(3x)(2y) ↙  (2y)2 − 49
Write the trinomial as a square.      (3x − 2y)2 − 49
Is this binomial a sum or difference? Of squares or cubes? Write it as a difference of squares.      (3x − 2y)2 − 72
Write it as a product of conjugates.          ((3x − 2y) −7)((3x − 2y) +7)(3x − 2y − 7)(3x − 2y + 7)
Is the expression factored completely? Yes.
Check by multiplying: (3x − 2y + 7)

9x2 − 6xy − 21x − 6xy + 4y2 + 14y + 21x − 14y − 49

 9x2 − 12xy + 4y2 − 49✓

Factoring Expressions with Fractional or Negative Exponents

Expressions with fractional or negative exponents can be factored by pulling out a GCF. Look for the variable or exponent that is common to each term of the expression and pull out that variable or exponent raised to the lowest power. These expressions follow the same factoring rules as those with integer exponents. For instance,  2x1/4 + 5x3/4 can be factored by pulling out x1/4 and being rewritten as x1/4(2 + 5x1/2).

Try it! – Factoring an Expression with Fractional or Negative Exponent Factor

Factor:  3x(x + 2)−1/3 + 4(x  +2)2/3.

Solution

Factor out the term with the lowest value of the exponent. In this case, that would be (x + 2)−1/3.

Factor out the GCF.                                           (x + 2)−1/3(3x + 4(x + 2))
Simplify.                                                              (x + 2)−1/3(3x + 4x + 8)
                                                                             (x + 2)−1/3(7x + 8)

Access these online resources for additional instruction and practice with factoring polynomials.

    Key Concepts

    Steps Algebraic
    difference of squares a2 − b2=(a + b)(a − b)
    perfect square trinomial a2 + 2ab + b2=(a + b)2
    sum of cubes a3 + b3=(a + b)(a2 − ab + b2)
    difference of cubes a3 − b3=(a − b)(a2 + ab + b2)
    1. Write the factors as two binomials with first terms x.
    2. Find two numbers m and n that
      • multiply to c, m · n = c
      • add to b, m + n = b
    3. Use m and n as the last terms of the factors.
      (x + m)(x + n)
    4. Check by multiplying the factors.
    • The greatest common factor, or GCF, can be factored out of a polynomial. Checking for a GCF should be the first step in any factoring problem.
    • Trinomials with leading coefficient 1 can be factored by finding numbers that have a product of the third term and a sum of the second term.
    • Trinomials can be factored using a process called factoring by grouping.
    • Perfect square trinomials and the difference of squares are special products and can be factored using equations.
    • The sum of cubes and the difference of cubes can be factored using equations.
    • Polynomials containing fractional and negative exponents can be factored by pulling out a GCF.
    definition

    License

    Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

    NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

    Share This Book