"

22 Polynomials

Topics Covered

Identifying the Degree and Leading Coefficient of Polynomials

We have learned that a term is a constant or the product of a constant and one or more variables. A monomial is an algebraic expression with one term. When it is of the form axm, where a is a constant and m is a whole number, it is called a monomial in one variable. Some examples of monomial in one variable are. Monomials can also have more than one variable such as and −4a2b3c2.

polynomial—A monomial, or two or more algebraic terms combined by addition or subtraction is a polynomial.

monomial—A polynomial with exactly one term is called a monomial.

binomial—A polynomial with exactly two terms is called a binomial.

trinomial—A polynomial with exactly three terms is called a trinomial.

Here are some examples of polynomials.

Type Ex. 1 Ex. 2 Ex. 3 Ex. 4
Polynomial y + 1 4a2 − 7ab + 2b2 4x4 + x3 + 8x2 − 9x+1
Monomial 14 8y2 −9x3y5 −13a3b2c
Binomial a + 7b 4x2 − y2 y2 − 16 3p3q − 9p2q
Trinomial x2 − 7x + 12 9m2 + 2mn − 8n2 6k4 − k3 + 8k z4 + 3z2 − 1

The degree of a polynomial and the degree of its terms are determined by the exponents of the variable.
A monomial that has no variable, just a constant, is a special case. The degree of a constant is then 0. In the table above, the example of monomial “14” would have a degree of 0.

The degree of a term is the sum of the exponents of its variables.

The degree of a constant is 0.

The degree of a polynomial is the highest degree of all its terms.

Let’s start by looking at a monomial. The monomial 8ab2 has two variables a and b. To find the degree we need to find the sum of the exponents. The variable a doesn’t have an exponent written, but remember that means the exponent is 1. The exponent of b is 2. The sum of the exponents, 1 + 2, is 3, so the degree is 3.

Try it!

Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. Then, find the degree of each polynomial.

a. 7y2 − 5y + 3  b. −2a4b2  c. 3x5 − 4x3 − 6x2 + x − 8  d. 2y−8xy3 ⓔ 15

Solution

Polynomial Number of terms Type Degree of terms Degree of polynomial
7y2 − 5y + 3 3 Trinomial 2, 1, 0  2
−2a4b2 1 Monomial 4, 2 6
3x5 − 4x3 − 6x2 + x − 8 5 Polynomial 5, 3, 2, 1, 0 5
2y − 8xy3 2 Binomial 1, 4 4
15 1 Monomial 0 0

A polynomial, which is a sum of or difference of terms, each consist of a variable raised to a nonnegative integer power. A number multiplied by a variable raised to an exponent, such as the 384 in  384x, is known as a coefficient.

Coefficients can be positive, negative, or zero, and can be whole numbers, decimals, or fractions. Each product aixi, such as 384xw, is a term of a polynomial. If a term does not contain a variable, it is called a constant.

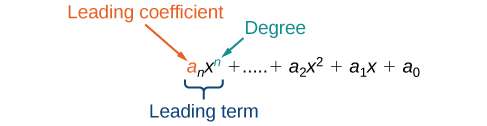
The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form.

A polynomial reading: a sub n times x to the nth power plus and so on plus a sub 2 times x squared plus a sub one times x plus a subzero is shown. The a in the term a sub n is labeled: leading coefficient. The n in the term x to the nth power is labeled: degree. Finally, the entire term is labeled as: Leading term.

Polynomials

A polynomial is an expression that can be written in the form anxn + … + a2x2 + a1x + a0

Each real number ai is called a coefficient. The number a0 that is not multiplied by a variable is called a constant. Each product aixi is a term of a polynomial. The highest power of the variable that occurs in the polynomial is called the degree of a polynomial. The leading term is the term with the highest power, and its coefficient is called the leading coefficient.

Given a polynomial expression, identify the degree and leading coefficient.

  1. Find the highest power of x to determine the degree.
  2. Identify the term containing the highest power of x to find the leading term.
  3. Identify the coefficient of the leading term.

 

Try it! – Identifying the Degree and Leading Coefficient of a Polynomial

For the following polynomials, identify the degree, the leading term, and the leading coefficient.

  1. 3 + 2x2 − 4x3     b. 5t5 − 2t3 + 7     c. 6p − p3 − 2

 Solution

  1. The highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, −4x3. The leading coefficient is the coefficient of that term, −4.
  2. The highest power of t is 5, so the degree is 5. The leading term is the term containing that degree, 5t5. The leading coefficient is the coefficient of that term, 5.
  3. The highest power of p is 3, so the degree is 3. The leading term is the term containing that degree, −p3, The leading coefficient is the coefficient of that term, −1.

Adding and Subtracting Polynomials

We can add and subtract polynomials by combining like terms, which are terms that contain the same variables raised to the same exponents. For example, 5x2 and −2x2 are like terms, and can be added to get 3x2, but 3x and 3x2 are not like terms, and therefore cannot be added.

Try it!

Add or subtract: a. 25y2 + 15y2       b.  16pq3 − (−7pq3).

Solution

a.

Steps Algebraic
Problem 25y2 + 15y2
Combine like terms.    40y2

b.

Steps Algebraic
Problem   16pq3 − (−7pq3)
Combine like terms. 23pq3

Given multiple polynomials, add or subtract them to simplify the expressions.

We can think of adding and subtracting polynomials as just adding and subtracting a series of monomial’s. Look for the like terms—those with the same variables and the same exponent.

The Commutative Property allows us to rearrange the terms to put like terms together.

  1. Combine like terms.
  2. Simplify and write in standard form.

Try it!

Find the sum:  (7y2 − 2y + 9) + (4y2 − 8y − 7).

Solution

Steps Algebraic
Identify like terms. (7y2 − 2y + 9)+(4y2 − 8y − 7)
Rewrite without the parentheses, rearranging to get the like terms together.      7y2 + 4y2 − 2y − 8y + 9 − 7
Combine like terms.            11y2 − 10y + 2

Try it! – Adding Polynomials

Find the sum.

(12x2 + 9x − 21) + (4x3 + 8x2 − 5x + 20)

Solution

Steps Algebraic
Combine like terms.            4x3 + (12x2 + 8x2) + (9x − 5x) + (−21 + 20)     
Simplify. 4x3 + 20x2 + 4x − 1

Analysis

We can check our answers to these types of problems using a graphing calculator. To check, graph the problem as given along with the simplified answer. The two graphs should be equivalent. Be sure to use the same window to compare the graphs. Using different windows can make the expressions seem equivalent when they are not.

Be careful with the signs as you distribute while subtracting the polynomials in the next example.

 

Tip!

Be careful with the signs as you distribute while subtracting the polynomials in the next example.

Try it!

Find the difference:  (9w2 − 7w + 5) − (2w2 − 4).

Solution

Steps Algebraic
Problem    (9w2 − 7w + 5) − (2w2 − 4)
Distribute and identify like terms.  9w2 − 7w + 5 – 2w2 + 4
Rearrange the terms.  9w2 − 2w2 − 7w + 5 + 4
Combine like terms. 7w2 − 7w + 9

Try it! – Subtracting Polynomials

Find the difference.

(7x4 − x2 + 6x + 1) − (5x3 − 2x2 + 3x + 2)

Solution

Steps Algebraic
Combine like terms.      7x4 − 5x3 + (−x2 + 2x2) + (6x − 3x) + (1 − 2)
Simplify.        7x4 − 5x3 + x2 + 3x − 1

Analysis

Note that finding the difference between two polynomials is the same as adding the opposite of the second polynomial to the first.

Multiplying Polynomials

Since monomials are algebraic expressions, we can use the properties of exponents to multiply monomials. Review Module 2 if you need to review exponent rules.

Try it!

Multiply:  a. (3x2)(−4x3)   b. (\frac{5}{6}x3y)(12xy2).

Solution

a.

Steps Algebraic
Problem  (3x2)(−4x3)
Use the Commutative Property to rearrange the terms. 3 · (−4) · x2 · x3
Multiply. -12x5

b. 

Steps Algebraic
Problem   (\frac{5}{6}x3y)(12xy2)
Use the Commutative Property to rearrange the terms. \frac{5}{6}·12·x3·x·y·y2
Multiply. 10x4y3

Multiplying a polynomial by a monomial is really just applying the Distributive Property.

Notice that before combining like terms, you have four terms. You multiply the two terms of the first binomial by the two terms of the second binomial—four multiplications.

Steps Algebraic
Distribute p This figure has two columns. In the first row, the right column contains the expression x plus 3, in parentheses, times p. Two red arrows extend from the p, terminating at x and 3.
We distributed the p to get: In the second row, the text in the left column says “We distributed the p to get”. The right column contains xp plus 3p. lus 10x plus 21.
What if we have (x + 7) instead of p? In the third row, the text in the left column says “What if we have x plus 7 instead of p?” In the right column is the product of two binomials, x plus 3 and x plus 7. Two red arrows extend from x plus 7, terminating at the x and the 3 in the first binomial.
Distribute (x + 7). In the fourth row, the text in the left column says “Think of the x plus 7 as the p above.” In the right column is x times x plus 7 plus 3 times x plus 7, where x plus 7 is in parentheses twice.
Distribute again. In the fifth row, the text in the left column says “Distribute x plus 7.” In the right column is x squared plus 7x plus 3x plus 21.
Combine like terms. In the sixth row, the text in the left column says “Combine like terms.” In the right column is x squared plus 10x plus 21.

Try it!

Multiply:  a. −2y(4y2 + 3y − 5)  b. 3x3y(x2 − 8xy + y2)

Solution

a.

Steps Algebraic
Example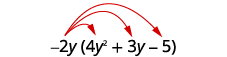
This figure shows how to distribute the multiplication of negative 2 y with the polynomial 4 y squared plus 3 y minus 5 in parentheses. Three arrows are drawn from the negative 2y pointing to each term in the polynomial in parentheses indicating the three multiplications.
Distribute.
The next line shows the result when the negative 2 y is distributed: negative 2 y times 4 y squared plus negative 2 y times 3 y minus negative 2 y times 5.
Multiply.
The simplified form is then negative 8 y to power of 3 minus 6 y to the power of 2 plus 10 y.

b.

Steps Algebraic
Example   3x3y(x2 − 8xy + y2)
Distribute      3x3y · x2 + (3x3y) · (−8xy) + (3x3y) · y2
Multiply.             3x5y − 24x4y2 + 3x3y3

 

Multiplying polynomials is a bit more challenging than adding and subtracting polynomials. We must use the distributive property to multiply each term in the first polynomial by each term in the second polynomial. We then combine like terms. We can also use a shortcut called the FOIL method when multiplying binomials. Certain special products follow patterns that we can memorize and use instead of multiplying the polynomials by hand each time. We will look at a variety of ways to multiply polynomials.

Multiplying Polynomials Using the Distributive Property

To multiply a number by a polynomial, we use the distributive property. The number must be distributed to each term of the polynomial. We can distribute the

2 in 2(x+7) to obtain the equivalent expression 2x+14. When multiplying polynomials, the distributive property allows us to multiply each term of the first polynomial by each term of the second. We then add the products together and combine like terms to simplify.

Given the multiplication of two polynomials, use the distributive property to simplify the expression.

  1. Multiply each term of the first polynomial by each term of the second.
  2. Combine like terms.
  3. Simplify.

 

Try it! – Multiplying Polynomials Using the Distributive Property

Find the product.

(2x + 1)(3x2 − x + 4)

Solution

 

Steps Algebraic
Use the distributive property. 2x(3×2 − x + 4) + (3×2 − x + 4)
Multiply.  (6x3 − 2x2 + 8x) + (3x2 − x + 4)
Combine like terms.   6x3 + (−2x2 + 3x2) + (8x − x) + 4
Simplify.           6x3 + x2 + 7x + 4
Analysis

We can use a table to keep track of our work. Write one polynomial across the top and the other down the side. For each box in the table, multiply the term for that row by the term for that column. Then add all of the terms together, combine like terms, and simplify.

—                          3x2                            -x                            +4
                         2x                          6x3                            -2x2                            8x
                         +1                          3x2                            -x                            +4

Try it!

Multiply (b + 3)(2b2 – 5b + 8) using a. the Distributive Property and b. the Vertical Method.

Solution

a.

Steps Algebraic
This figure shows how to distribute the multiplication of b plus 3 in parentheses with 2 b squared minus 5 b plus 8 in parentheses.
Distribute. After distributing the trinomial the result is b times the quantity 2 b squared minus 5 b plus 8 in parentheses plus 3 times the quantity 2 b squared minus 5 b plus 8 in parentheses 2 y minus 5 in parentheses.
Multiply. Then we distribute the b to the trinomial to get 2 b to the power of 3 minus 5 b squared plus 8 b and distribute the 3 to the trinomial to get 6 b squared minus 15 b plus 24.
Combine like terms. Combining like terms results in the simplified form 2 b to power of 3 plus b squared minus 7 b plus 24.

b. It is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way.

Steps Algebraic
Multiply (2b2 − 5b + 8) by 3.                                                
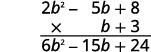 This figure shows how to multiply the polynomials with the vertical method. The polynomial 2 b squared minus 5 b plus 8 is written directly over the polynomial b plus 3. The 8 is directly over the 3 and the negative 5 b is directly over the b. A horizontal line is drawn below the b plus 3. The result of multiplying 3 with the quantity 2 b squared minus 5 b plus 8 is written below the horizontal line. The result is get 6 b squared minus 15 b plus 24 with the 24 under the 3 and 8. The result of multiplying the b with the quantity 2 b squared minus 5 b plus 8 is written below the last calculation but shifted one term to the left. The result is 2 b to the power of 3 minus 5 b squared plus 8 b with the 8 b under the negative 15 b from the first multiplication. A second horizontal line is draw below the last result. The two multiplications are then added column by column. 24 is brought down since nothing is below it. Negative 15 b is added to 8 b to get negative 7 b. 6 b squared is added to negative 5 b squared to get b squared. 2 b to the power of 3 is brought down since nothing is above it. The final result is 2 b to power of 3 plus b squared minus 7 b plus 24.
Multiply (2b2 − 5b + 8) by b. The result of multiplying the b with the quantity 2 b squared minus 5 b plus 8 is written below the last calculation but shifted one term to the left. The result is 2 b to the power of 3 minus 5 b squared plus 8 b with the 8 b under the negative 15 b from the first multiplication. A second horizontal line is draw below the last result.
Combine like terms. The two multiplications are then added column by column. 24 is brought down since nothing is below it. Negative 15 b is added to 8 b to get negative 7 b. 6 b squared is added to negative 5 b squared to get b squared. 2 b to the power of 3 is brought down since nothing is above it. The final result is 2 b to power of 3 plus b squared minus 7 b plus 24.

 

Using FOIL to Multiply Binomials

A shortcut called FOIL is sometimes used to find the product of two binomials. It is called FOIL because we multiply the first terms, the outer terms, the inner terms, and then the last terms of each binomial.

Two quantities in parentheses are being multiplied, the first being: a times x plus b and the second being: c times x plus d. This expression equals ac times x squared plus ad times x plus bc times x plus bd. The terms ax and cx are labeled: First Terms. The terms ax and d are labeled: Outer Terms. The terms b and cx are labeled: Inner Terms. The terms b and d are labeled: Last Terms.

The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial, and then combining like terms.

Given two binomials, use FOIL to simplify the expression.

The figure shows how to use the FOIL method to multiply two binomials. The example is the quantity a plus b in parentheses times the quantity c plus d in parentheses. The numbers a and c are labeled first and the numbers b and d are labeled last. The numbers b and c are labeled inner and the numbers a and d are labeled outer. A note on the side of the expression tells you to Say it as you multiply! FOIL First Outer Inner Last. The directions are then given in numbered steps. Step 1. Multiply the First terms. Step 2. Multiply the Outer terms. Step 3. Multiply the Inner terms. Step 4. Multiply the Last Terms. Step 5. Combine like terms when possible.

Try it! – Using FOIL to Multiply Binomials

Use FOIL to find the product:  (2x – 18)(3x + 3)

Solution

Find the product of the first terms.

Shows 2x -18, a blue arrow connects the 2x to another expressions 3x+3. On the right shows the expression 2x times 3x equals 3x squared.

Find the product of the outer terms.

Shows 2x-18 and the expression 3x+3. A blue arrow connects the 2x to the 3 in the 2nd. To the right is the equation 2x-3 = 6x

Find the product of the inner terms.

Shows the expression 2x-8 and 3x+3, with a blue arrow linking the -18 and 3x. On the right is the result: -18x times 3x = -54x

Find the product of the last terms.

Shows 2x-18 and 3x+3, with a blue arrow linking the -18 and 3 of the 2nd expression. On the right shows the result: -18 times 3 is -54

Add the products.                                                                                                                                                                       6x2 + 6x − 54x − 54

Combine like terms.                                                                                                                                                                   6x2 + (6x − 54x) − 54

Simplify.                                                                                                                                                                                       6x2 − 48x − 54

The FOIL method is usually the quickest method for multiplying two binomials, but it only works for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

This figure shows the vertical multiplication of 23 and 46. The number 23 is above the number 46. Below this, there is the partial product 138 over the partial product 92. The final product is at the bottom and is 1058. Text on the right side of the image says “Start by multiplying 23 by 6 to get 138. Next, multiply 23 by 4, lining up the partial product in the correct columns. Last you add the partial products.”

Try it!

Multiply using the Vertical Method:

(3y − 1)(2y − 6)

Solution

It does not matter which binomial goes on the top.

Steps Algebraic
Multiply 3y – 1 by −6.
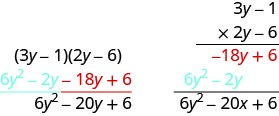Multiply 3y − 1 by 2y.Combine like terms.		 This figure has two columns. In the left column is the product of two binomials, 3y minus 1 and 2y minus 6. Below this is 6y squared minus 2y minus 18y plus 6. Below this is 6y squared minus 20y plus 6. In the right column is the vertical multiplication of 3y minus 1 and 2y minus 6. Below this is the partial product negative 18y plus 6. Below this is the partial product 6y squared minus 2y. Below this is 6y squared minus 20y plus 6.

 

Notice the partial products are the same as the terms in the FOIL method.

Sum or Difference (aka Difference of Squares or Conjugates)

Another special product is called the difference of squares, or Sum and Difference of Two Terms (as its called in the Algebra book.

A pair of binomials that each have the same first term and the same last term, but one is a sum and one is a difference is called a conjugate pair and is of the form

(a − b), (a + b).

Notice how each pair has one sum and one difference.

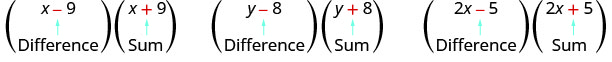
This figure has three products. The first is x minus 9, in parentheses, times x plus 9, in parentheses. Below the x minus 9 is the word “difference”. Below x plus 9 is the word “sum”. The second is y minus 8, in parentheses, times y plus 8, in parentheses. Below y minus 8 is the word “difference”. Below y plus 8 is the word “sum”. The last is 2x minus 5, in parentheses, times 2x plus 5, in parentheses. Below the 2x minus 5 is the word “difference” and below 2x plus 5 is the word “sum”.

The figure shows two examples of multiplying a binomial with its conjugate. In the first example x plus 9 is multiplied with x minus 9 to get x squared minus 9 x plus 9 x minus 81 which simplifies to x squared minus 81. Colors show that x squared comes from the square of the x in the original binomial and 81 comes from the square of the 9 in the original binomial. In the secondexample 2 x minus 5 is multiplied with 2 x plus 5 to get 4 x squared plus 10 x minus 10 x minus 25 which simplifies to 4 x squared minus 25. Colors show that 4 x squared comes from the square of the 2 x in the original binomial and 25 comes from the square of the 5 in the original binomial.

Because the sign changes in the second binomial, the outer and inner terms cancel each other out, and we are left only with the square of the first term minus the square of the last term.

Difference of Squares or Sum and Difference

When a binomial is multiplied by a binomial with the same terms separated by the opposite sign, the result is the square of the first term minus the square of the last term.


This figure is divided into two sides. On the left side is the following formula: the product of a minus b and a plus b equals a squared minus b squared. On the right side is the same formula labeled: a minus b and a plus b are labeled “conjugates”, the a squared and b squared are labeled squares and the minus sign between the squares is labeled “difference”. Therefore, the product of two conjugates is called a difference of squares.

 

Try it!

Multiply:     (x − 8)(x + 8).

Solution

First, recognize this as a product of conjugates. The binomials have the same first terms, and the same last terms, and one binomial is a sum and the other is a difference.

Steps Algebraic
It fits the pattern. The product of x minus 8 and x plus 8. Above this is the general form a minus b, in parentheses, times a plus b, in parentheses.
Square the first term, x. x squared minus blank. Above this is the general form a squared minus b squared.
Square the last term, 8. x squared minus 8 squared.
The product is a difference of squares. x squared minus 64. with a squared of the x minus b squared over the 64.

Binomial (Perfect) Square Trinomials

Certain binomial products have special forms. When a binomial is squared, the result is called a perfect square trinomial. We can find the square by multiplying the binomial by itself. However, there is a special form that each of these perfect square trinomials takes, and memorizing the form makes squaring binomials much easier and faster. Let’s look at a few perfect square trinomials to familiarize ourselves with the form.

(x + 5)2 = x2 + 10x + 25

(x − 3)2 = x2 − 6x + 9 

(4x − 1)2 = 16x2 − 8x + 1

Notice that the first term of each trinomial is the square of the first term of the binomial and, similarly, the last term of each trinomial is the square of the last term of the binomial. The middle term is double the product of the two terms. Lastly, we see that the first sign of the trinomial is the same as the sign of the binomial.

 

Perfect Square Trinomials

When a binomial is squared, the result is the first term squared added to double the product of both terms and the last term squared.

(x + a)2 = (x + a)(x + a) = x2 + 2ax + a2

Or


The figure shows the result of squaring two binomials. The first example is a plus b squared equals a squared plus 2 a b plus b squared. The equation is written out again with each part labeled. The quantity a plus b squared is labeled binomial squared. The terms a squared is labeled first term squared. The term 2 a b is labeled 2 times product of terms. The term b squared is labeled last term squared. The second example is a minus b squared equals a squared minus 2 a b plus b squared. The equation is written out again with each part labeled. The quantity a minus b squared is labeled binomial squared. The terms a squared is labeled first term squared. The term negative 2 a b is labeled 2 times product of terms. The term b squared is labeled last term squared.

Given a binomial, square it using the formula for perfect square trinomials.

  1. Square the first term of the binomial.
  2. Square the last term of the binomial.
  3. For the middle term of the trinomial, double the product of the two terms.
  4. Add and simplify.

 

Try it!

Multiply:  a. (x + 5)2  b. (2x − 3y)2.

a.

Steps Algebraic
Example The example shows how to multiply x plus 5 squared wiht a plus b written above the expression.

 
Square the first term.
Using the formula a squared plus 2 a b plus b squared. Squaring the first term results in x squared which matches up with the term a squared in the formula. Image shows x square with a squared in red above it + blank with 2ab above that, + blank with b squared above that.
Square the last term.
Squaring the last term results in 5 squared which matches up with the term b squared in the formula. So x squared under the a squared of the formula, + blank under the 2ab of the formula, + 5 squared under the b squared of the formula.
Double their product.
Doubling the product results in 2 times x times 5 which matches up with 2 a b in the formula.
Simplify.
The simplified version is x squared plus 10 x plus 25.

b.

Steps Algebraic
Example
The example shows how to multiply 2 x minus 3 y squared using the formula, with a minus b labelling the 2x and 3y.
Use the pattern.
Squaring the first term results in 2 x squared which matches up with the term a squared in the formula. Squaring the last term results in 3 y squared which matches up with the term b squared in the formula. Doubling the product results in 2 times 2 x times 3 y which matches up with 2 a b in the formula.
Simplify.
The simplified version is 4 x squared minus 12 x y plus 9 y squared.

Try it!

Expand (4x − 1)2.

Solution

16x2 − 8x + 1

Performing Operations with Polynomials of Several Variables

We have looked at polynomials containing only one variable. However, a polynomial can contain several variables. All of the same rules apply when working with polynomials containing several variables. Consider an example:

(a + 2b)(4a − b − c)

Steps Algebraic
Use the distributive property.                                                          a(4a − b − c) + 2b(4a − b − c)
Multiply.     4a2 − ab − ac + 8ab − 2b2 − 2bc
Combine like terms.      4a2 + (−ab + 8ab) − ac − 2b2 – 2bc
Simplify.   4a2 + 7ab − ac − 2bc − 2b2

 

Try it!

Find the sum:  (u2 − 6uv + 5v2) + (3u2 + 2uv)
Solution:
Steps Algebraic
Use the distributive property.                                                           u2 − 6uv + 5v2 + 3u2 + 2uv
Rearrange the terms to put like terms together. u2 + 3u2 − 6uv + 2uv + 5v2
Combine like terms.   4u2 − 4uv + 5v2

Try it! – Multiplying Polynomials Containing Several Variables

Multiply  (x + 4)(3x − 2y + 5).

Solution

Follow the same steps that we used to multiply polynomials containing only one variable.

Steps Algebraic
Use the distributive property.                                                       x(3x − 2y + 5) + 4(3x − 2y + 5)
Multiply.      3x2 − 2xy + 5x + 12x − 8y + 20
Combine like terms.     3x2 − 2xy + (5x + 12x) − 8y + 20
Simplify.      3x2 − 2xy + 17x − 8y + 20

Try it!

Multiply  (3x − 1)(2x + 7y − 9).

Solution

6x2 + 21xy − 29x − 7y + 9

Access these online resources for additional instruction and practice with polynomials.

    Key Concepts

    • A polynomial is a sum of terms each consisting of a variable raised to a non-negative integer power. The degree is the highest power of the variable that occurs in the polynomial. The leading term is the term containing the highest degree, and the leading coefficient is the coefficient of that term.
    • We can add and subtract polynomials by combining like terms.
    • To multiply polynomials, use the distributive property to multiply each term in the first polynomial by each term in the second. Then add the products.
    • FOIL (First, Outer, Inner, Last) is a shortcut that can be used to multiply binomials.
    • Perfect square trinomials and difference of squares are special products.
    • Follow the same rules to work with polynomials containing several variables.
    Binomial Squares Sum or Difference (Product of Conjugates)
    (a + b)2 = a2 + 2ab + b2 (a − b)(a + b) = a2 − b2
    (a − b)2 = a2 − 2ab + b2
    Squaring a binomial Multiplying conjugates
    Product is a trinomial Product is a binomial.
    Inner and outer terms with FOIL are the same. Inner and outer terms with FOIL are opposites.
    Middle term is double the product of the terms There is no middle term.
    definition

    License

    Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

    NCB 0502 - Support for Corequisite Algebra Copyright © by Elizabeth Pople is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

    Share This Book