18 Radicals and Rational Exponents
Topics Covered
-
- Simplify Expressions with Roots
- Product Property to Simplify Roots
- Quotient Property to Simplify Roots
- Add, Subtract Square Roots
- Rationalize Denominators
- Simplify Expressions with Nth Roots
- Product Rule with Nth Roots
- Quotient Rule with Nth Roots
- Rational Exponents in
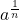 form
form - Rational Exponents in
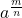 form
form - Use the Properties of Exponents to Simplify Expressions with Rational Exponents
- Key Concepts
Simplify Expressions with Roots
Remember that when a real number n is multiplied by itself, we write n2 and read it ‘n squared’. This number is called the square of n, and n is called the square root. For example,
Square and Square Root of a number
Square
Square Root
Notice (−13)2 = 169 also, so −13 is also a square root of 169. Therefore, both 13 and −13 are square roots of 169.
So, every positive number has two square roots—one positive and one negative. What if we only wanted the positive square root of a positive number? We use a radical sign, and write, ![]() , which denotes the positive square root of m. The positive square root is also called the principal square root.
, which denotes the positive square root of m. The positive square root is also called the principal square root.
We also use the radical sign for the square root of zero. Because ![]() . Notice that zero has only one square root.
. Notice that zero has only one square root.
Square Root Notation
We know that every positive number has two square roots and the radical sign indicates the positive one. We write ![]() . If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example,
. If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, ![]() .
.
Try it!
Simplify: a. ![]() b.
b. ![]()
Solution:
a.
| Steps | Algebraic |
| Problem | |
| Since 122 = 144. | 12 |
b.
| Steps | Algebraic |
| Problem | |
| Since 172 = 289 and the negative is in front of the radical sign. | -17 |
Can we simplify ![]() ? Is there a number whose square is −49?
? Is there a number whose square is −49?
Any positive number squared is positive. Any negative number squared is positive. There is no real number equal to ![]() . The square root of a negative number is not a real number.
. The square root of a negative number is not a real number.
Try it!
Simplify: a. ![]() b.
b. ![]()
Solution:
a.
| Steps | Algebraic |
| Problem | |
| There is no real number whose square is −196. |
b.
| Steps | Algebraic |
| Problem | |
| The negative is in front of the radical. | -8 |
But what if we want to estimate ![]() ? If we simplify the square root first, we’ll be able to estimate it easily. There are other reasons, too, to simplify square roots as you’ll see later in this section.
? If we simplify the square root first, we’ll be able to estimate it easily. There are other reasons, too, to simplify square roots as you’ll see later in this section.
Simplified Square Root
![]() is considered simplified if a (radicand) has no perfect square factors.
is considered simplified if a (radicand) has no perfect square factors.
So ![]() is simplified. But
is simplified. But ![]() is not simplified, because 16 is a perfect square factor of 32.
is not simplified, because 16 is a perfect square factor of 32.
Use Product Property to Simplify Square Roots
The properties we will use to simplify expressions with square roots are similar to the properties of exponents. We know that (ab)m = ambm. The corresponding property of square roots says that ![]() .
.
Product Property of Square Roots
If a, b are non-negative real numbers, then
We use the Product Property of Square Roots to remove all perfect square factors from a radical.
Try it!
Simplify: ![]() .
.
Solution:



Notice in the previous example that the simplified form of ![]() is
is ![]() , which is the product of an integer and a square root. We always write the integer in front of the square root.
, which is the product of an integer and a square root. We always write the integer in front of the square root.
Simplify a square root using the product property.
- Find the largest perfect square factor of the radicand. Rewrite the radicand as a product using the perfect-square factor.
- Use the product rule to rewrite the radical as the product of two radicals.
- Simplify the square root of the perfect square.
Try it!
Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Problem | |
| Rewrite the radicand as a product using the largest perfect square factor. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
The next example is much like the previous examples, but with variables.
Try it!
1. Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Problem | |
| Rewrite the radicand as a product using the largest perfect square factor. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
2. Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Problem | |
| Rewrite the radicand as a product using the largest perfect square factor. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
So we can multiply ![]() in this way:
in this way:
![]()
![]()
![]()
Even when the product is not a perfect square, we must look for perfect-square factors and simplify the radical whenever possible.
Try it!
Simplify: a. ![]() b.
b. ![]() .
.
Solution:
a.
| Steps | Algebraic |
| Problem | |
| Multiply using the Product Property. | |
| Simplify the radical. | |
| Simplify. |
b.
| Steps | Algebraic |
| Problem | |
| Multiply using the Product Property. | |
| Simplify the radical. | |
| Simplify. |
Notice that in (b) we multiplied the coefficients and multiplied the radicals. Also, we did not simplify ![]() . We waited to get the product and then simplified.
. We waited to get the product and then simplified.
Try it!
Simplify: a. ![]() b.
b. ![]()
| Steps | Algebraic |
| Problem | |
| Multiply using the Product Property. | |
| Simplify the radical. | |
| Simplify. |
b.
| Steps | Algebraic |
| Problem | |
| Multiply using the Product Property. | |
| Simplify the radical. |
Quotient Property with Roots
Whenever you have to simplify a square root, the first step you should take is to determine whether the radicand is a perfect square. A perfect square fraction is a fraction in which both the numerator and the denominator are perfect squares.
Try it!
Simplify: ![]()
Solution:
| Steps | Algebraic |
| Problem | |
| Since |
|
If the numerator and denominator have any common factors, remove them. You may find a perfect square fraction!
Try it!
Simplify: ![]()
Solution:
| Steps | Algebraic |
| Problem | |
| Simplify inside the radical first. | |
| Rewrite showing the common factors of the numerator and denominator. | |
| Simplify. |
|
In the last example, our first step was to simplify the fraction under the radical by removing common factors. In the next example, we will use the Quotient Property to simplify under the radical. We divide the like bases by subtracting their exponents, ![]() .
.
Try it!
Simplify: 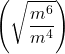
Solution:
| Steps | Algebraic |
| Problem | |
| Simplify the fraction inside the radical first. | |
| Divide the like bases by subtracting the exponents. | |
| Simplify. | |
Remember the Quotient to a Power Property? It said we could raise a fraction to a power by raising the numerator and denominator to the power separately.
![]()
We can use a similar property to simplify a square root of a fraction. After removing all common factors from the numerator and denominator, if the fraction is not a perfect square, we simplify the numerator and denominator separately.
Quotient Property of Square Roots
If a, b are non-negative real numbers and b ≠ 0, then
![]()
Try it!
Simplify: 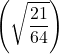 .
.
| Steps | Algebraic |
| Problem | |
| We cannot simplify the fraction inside the radical. Rewrite using the quotient property. | 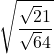 |
| Simplify the square root of 64. The numerator cannot be simplified. |
We will use the Quotient Property for Exponents, ![]() =
= ![]() , when we have variables with exponents in the radicands.
, when we have variables with exponents in the radicands.
Try it!
1. Simplify: ![]() .
.
| Steps | Explanation | Algebraic |
| Step 1. Simplify the fraction in the radicand, if possible. |
|
|
| Step 2. Use the Quotient Property to rewrite the radicals as the quotient of two radicals. | We rewrite
|
|
| Step 3. Simplify the radicals in the numerator and enumerator. |
|
2. Simplify: 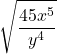 .
.
Solution:
| Steps | Algebraic |
| Problem | 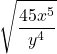 |
| We cannot simplify the fraction in the radicand. Rewrite using the Quotient Property. | |
| Simplify the radicals in the numerator and the denominator. | |
| Simplify. | |
3. Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Problem | |
| Simplify the fraction in the radicand. | |
| Rewrite using the Quotient Property | |
| Simplify the radicals in the numerator and the denominator. | |
| Simplify. |
4. Simplify: ![]() .
.
Solution:
| Steps | Algebraic |
| Problem | |
| Neither radicand is a perfect square, so rewrite using the quotient property of square roots. | |
| Remove common factors in the numerator and denominator. | 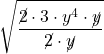 |
| Simplify. | |
| Simplify the radical. |
We will use the Quotient Property of Square Roots ‘in reverse’ when the fraction we start with is the quotient of two square roots, and neither radicand is a perfect square. When we write the fraction in a single square root, we may find common factors in the numerator and denominator.
Try it!
Simplify: ![]() .
.
| Steps | Algebraic |
| Problem | |
| Neither radicand is a perfect square, so rewrite using the quotient property of square roots. | |
| Remove common factors in the numerator and denominator. | |
| Simplify. | |
Add, Subtract Square Roots
We know that we must follow the order of operations to simplify expressions with square roots. The radical is a grouping symbol, so we work inside the radical first. We simplify ![]() in this way:
in this way:
| Expression | |
| Add inside the radical. | |
| Simplify. |
So if we have to add ![]() , we must not combine them into one radical.
, we must not combine them into one radical.
![]() ≠
≠ ![]()
Trying to add square roots with different radicands is like trying to add unlike terms.
But, just like we can add x + x = 2x, we can add ![]() .
.
Adding square roots with the same radicand is just like adding like terms. We call square roots with the same radicand like square roots to remind us they work the same as like terms.
Square roots with the same radicand are called like square roots.
We add and subtract like square roots in the same way we add and subtract like terms. We know that 3x + 8x is 11x.
Similarly we add ![]() and the result is
and the result is ![]()
Think about adding like terms with variables as you do the next few examples. When you have like radicands, you just add or subtract the coefficients. When the radicands are not like, you cannot combine the terms.
Try it!
Simplify: ![]() .
.
| Steps | Algebraic |
| Expression | |
| Since the radicals are like, we subtract the coefficients |
2. Simplify: ![]() .
.
| Steps | Algebraic |
| Expression | |
| Since the radicals are like, we subtract the coefficients |
Remember that we always simplify square roots by removing the largest perfect-square factor. Sometimes when we have to add or subtract square roots that do not appear to have like radicals, we find like radicals after simplifying the square roots.
Try it!
Simplify: ![]()
| Steps | Algebraic |
| Expression | |
| Simplify the radicals, when possible. |
|
| Combine the like radicals. |
Tip!
Just like we use the Associative Property of Multiplication to simplify 5(3x) and get 15x, we can simplify ![]() and get
and get ![]() .
.
We will use the Associative Property to do this in the next example.
Try it!
Simplify: ![]()
| Steps | Algebraic |
| Example | |
| Simplify the radicals. |
|
| Combine the like radicals. |
Try it!
Simplify: ![]()
Solution:
| Steps | Algebraic |
| ExampleExample | |
| Simplify the radicals. |
|
| Combine the like radicals. |
Rationalize Denominators
Before the calculator became a tool of everyday life, approximating the value of a fraction with a radical in the denominator was a very cumbersome process!
For this reason, a process called rationalizing the denominator was developed. A fraction with a radical in the denominator is converted to an equivalent fraction whose denominator is an integer. Square roots of numbers that are not perfect squares are irrational numbers. When we rationalize the denominator, we write an equivalent fraction with a rational number in the denominator.
| Suppose we need an approximate value for the fraction. | |
| A five decimal place approximation to |
|
| Without a calculator, would you want to do this division? |
But we can find a fraction equivalent to ![]() by multiplying the numerator and denominator by
by multiplying the numerator and denominator by ![]() .
.
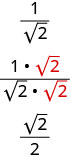 Now if we need an approximate value, we divide
Now if we need an approximate value, we divide ![]() . This is much easier.
. This is much easier.
Even though we have calculators available nearly everywhere, a fraction with a radical in the denominator still must be rationalized. It is not considered simplified if the denominator contains a square root.
A square root is considered simplified if there are
- no perfect-square factors in the radicand
- no fractions in the radicand
- no square roots in the denominator of a fraction
To rationalize a denominator with a square root, we use the property that ![]() . If we square an irrational square root, we get a rational number.
. If we square an irrational square root, we get a rational number.
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
To rationalize a denominator with one term, we can multiply a square root by itself. To keep the fraction equivalent, we multiply both the numerator and denominator by the same factor.
a.
| Steps | Algebraic |
| Example | |
| Multiply both the numerator and denominator by |
|
| Simplify. |
b. We always simplify the radical in the denominator first, before we rationalize it. This way the numbers stay smaller and easier to work with.
| Steps | Algebraic |
| Example | |
| The fraction is not a perfect square, so rewrite using the Quotient Property. | |
| Simplify the denominator. | |
| Multiply the numerator and denominator by |
|
| Simplify. | |
| Simplify. |
c.
| Steps | Algebraic |
| Example | |
| Multiply the numerator and denominator by |
|
| Simplify. | |
| Simplify. |
When the denominator of a fraction is a sum or difference with square roots, we use the Product of Conjugates pattern to rationalize the denominator.
| (a − b)(a + b) | |
| a2 − b2 | |
| -1 |
Try it!
1. Simplify: ![]()
| Steps | Algebraic |
| Example | |
| Multiply the numerator and denominator by the conjugate of the denominator. | |
| Multiply the conjugates in the denominator. | |
| Simplify the denominator. | |
| Simplify the denominator. | |
| Remove common factors from the numerator and denominator. | |
| We leave the numerator in factored form to make it easier to look for common factors after we have simplified the denominator. | |
2. Simplify: ![]()
| Steps | Algebraic |
| Example | |
| Multiply the numerator and denominator by the conjugate of the denominator. | |
| Multiply the conjugates in the denominator. | |
| Simplify the denominator. |
Simplify Variable Expressions with Roots
So far we have only talked about squares and square roots. Let’s now extend our work to include higher powers and higher roots.
Let’s review some vocabulary first.
| We write: | We say: |
| n2 | n squared |
| n3 | n cubed |
| n4 | n to the fourth power |
| n5 | n to the fifth power |
The terms ‘squared’ and ‘cubed’ come from the formulas for area of a square and volume of a cube.
It will be helpful to have a table of the powers of the integers from −5 to 5.
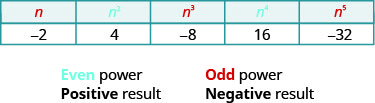
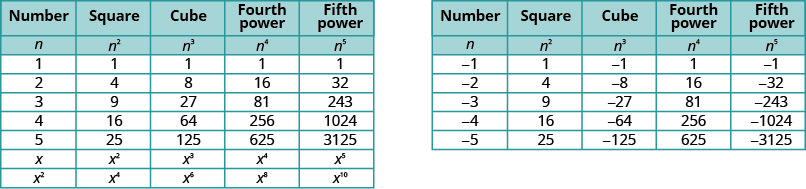 Notice the signs in the table. All powers of positive numbers are positive, of course. But when we have a negative number, the even powers are positive and the odd powers are negative. We’ll copy the row with the powers of −2 to help you see this.
Notice the signs in the table. All powers of positive numbers are positive, of course. But when we have a negative number, the even powers are positive and the odd powers are negative. We’ll copy the row with the powers of −2 to help you see this.
We will now extend the square root definition to higher roots.
nth Root of a Number
Just like we use the word ‘cubed’ for b3, we use the term ‘cube root’ for ![]() .
.
We can refer to the table of powers of the integers from -5 to 5 to help find higher roots.
Could we have an even root of a negative number? We know that the square root of a negative number is not a real number. The same is true for any even root. Even roots of negative numbers are not real numbers. Odd roots of negative numbers are real numbers.
Properties of ![Rendered by QuickLaTeX.com \displaystyle \boldsymbol{\sqrt[n]{a}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-90bdecb50ec8776e17c46eca45278946_l3.png)
When n is an even number and
- a ≥ 0, then
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c64bb5ee91e0e0e9f4f4abba832b5625_l3.png) is a real number.
is a real number. - a < 0, then
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c64bb5ee91e0e0e9f4f4abba832b5625_l3.png) is not a real number.
is not a real number.
When n is an odd number, ![]() is a real number for all values of a.
is a real number for all values of a.
We will apply these properties in the next two examples.
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]() .
.
Solution
a.
| Steps | Algebraic |
| Example | |
| Since |
b.
| Steps | Algebraic |
| Example | |
| Since |
c.
| Steps | Algebraic |
| Example | |
| Since |
In this example be alert for the negative signs as well as even and odd powers.
Exercises
Simplify: a. ![]() b.
b. ![]() c.
c. ![]() .
.
Solution
a.
| Steps | Algebraic |
| Example | |
| Since |
b.
| Steps | Algebraic |
| Example | |
| Think, (?)4 = −16. No real number raised to the fourth power is negative. | Not a real number. |
c.
| Steps | Algebraic |
| Example | |
| Since |
The odd root of a number can be either positive or negative. For example,
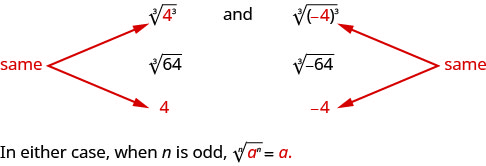
But what about an even root? We want the principal root, so ![]() .
.
But notice,
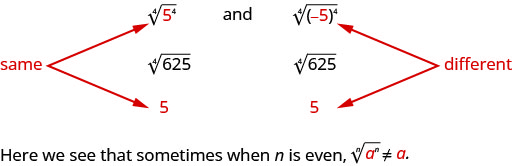
How can we make sure the fourth root of −5 raised to the fourth power is 5? We can use the absolute value. |−5| = 5. So we say that when n is even ![]() . This guarantees the principal root is positive.
. This guarantees the principal root is positive.
Simplifying Odd and Even Roots (nth root of Perfect nth power)
| when the index n is odd | |
| when the index n is even |
We must use the absolute value signs when we take an even root of an expression with a variable in the radical.
Try it!
1. Simplify: a. ![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
Solution:
a. We use the absolute value to be sure to get the positive root.
| Steps | Algebraic |
| Example | |
| Since the index n is even, |
b. This is an odd indexed root so there is no need for an absolute value sign.
| Steps | Algebraic |
| Example | |
| Since the index n is odd, |
c.
| Steps | Algebraic |
| Since the index n is even, |
d.
| Steps | Algebraic |
| Example | |
| Since the index n is odd, |
2. Simplify: a. ![]() b.
b. ![]() .
.
Solution:
a.
| Steps | Algebraic |
| Example | |
| Since |
|
| Since the index n is even, |
b.
| Steps | Algebraic |
| Example | |
| Since |
|
| Since the index n is even, |
|
| In this case the absolute value sign is not needed as |
|
The next example uses the same idea for higher roots.
Try it!
Simplify: a. ![]() b.
b. ![]() .
.
Solution
a.
| Steps | Algebraic |
| Example | |
| Since |
|
| Since the index n is odd, |
b.
| Steps | Algebraic |
| Example | |
| Since |
|
| Since |
Access this online resource for additional instruction and practice with simplifying expressions with roots.
Simplifying Variables Exponents with Roots using Absolute Values
Use Product and Quotient Rule to Simplify
We will simplify radical expressions in a way similar to how we simplified fractions. A fraction is simplified if there are no common factors in the numerator and denominator. To simplify a fraction, we look for any common factors in the numerator and denominator.
A radical expression, ![]() is considered simplified if it has no factors of mn. So, to simplify a radical expression, we look for any factors in the radicand that are powers of the index.
is considered simplified if it has no factors of mn. So, to simplify a radical expression, we look for any factors in the radicand that are powers of the index.
Simplified Radical Expression
For real numbers a and m, and n ≥ 2,
For example, ![]() is considered simplified because there are no perfect square factors in 5. But
is considered simplified because there are no perfect square factors in 5. But ![]() is not simplified because 12 has a perfect square factor of 4.
is not simplified because 12 has a perfect square factor of 4.
Similarly, ![]() is simplified because there are no perfect cube factors in 4. But
is simplified because there are no perfect cube factors in 4. But ![]() is not simplified because 24 has a perfect cube factor of 8.
is not simplified because 24 has a perfect cube factor of 8.
To simplify radical expressions, we will also use some properties of roots. The properties we will use to simplify radical expressions are similar to the properties of exponents. We know that (ab)n = an bn. The corresponding of Product Property of Roots says that ![]() .
.
Product Property of nth Roots
If ![]() and
and ![]() are real numbers, and
are real numbers, and ![]() is an integer, then
is an integer, then
![]()
Try it!
Simplify: ![]()
Solution:
| Steps | Algebraic |
| Step 1. Find the largest factor in the radicand that is a perfect power of the index.
Rewrite the the radicand as a product of two factors, using that factor.
|
We see that 49 is the largest factor of 98 that has a power of 2. In other words, 49 is the largest perfect square factor of 98.
|
| Step 2. Use the product rule to rewrite the radical as the product of two radicals. Always write the perfect square factor first. | |
| Step 3. Simplify the root of the perfect power. |
Simplify a radical expression using the Product Property.
- Find the largest factor in the radicand that is a perfect power of the index. Rewrite the radicand as a product of two factors, using that factor.
- Use the product rule to rewrite the radical as the product of two radicals.
- Simplify the root of the perfect power.
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
a.
| Steps | Algebraic |
| Example | |
| Rewrite the radicand as a product using the largest perfect square factor. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
b.
| Steps | Algebraic |
| Example | |
| Rewrite the radicand as a product using the largest perfect cube factor. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
c.
| Steps | Algebraic |
| Example | |
| Rewrite the radicand as a product using the greatest perfect fourth power factor. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
Using Quotient Property to Simplify
Whenever you have to simplify a radical expression, the first step you should take is to determine whether the radicand is a perfect power of the index. If not, check the numerator and denominator for any common factors, and remove them. You may find a fraction in which both the numerator and the denominator are perfect powers of the index.
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
a.
| Steps | Algebraic |
| Example | |
| Simplify inside the radical first.
Rewrite showing the common factors of the numerator and denominator. |
|
| Simplify the fraction by removing common factors. | |
| Simplify. Note |
b.
| Steps | Algebraic |
| Example | |
| Simplify inside the radical first.
Rewrite showing the common factors of the numerator and denominator. |
|
| Simplify the fraction by removing common factors. | |
| Simplify. Note |
c.
| Steps | Algebraic |
| Example | |
| Simplify inside the radical first.
Rewrite showing the common factors of the numerator and denominator. |
|
| Simplify the fraction by removing common factors. | |
| Simplify. Note |
In the next example we will use the Quotient Property to simplify under the radical. We divide the like bases by subtracting their exponents,
![]()
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
a.
| Steps | Algebraic |
| Example | |
| Simplify the fraction inside the radical first.
Divide the like bases by subtracting the exponents. |
|
| Simplify. |
b.
| Steps | Algebraic |
| Example | |
| Use the Quotient Property of exponents to simplify the fraction under the radical first. | |
| Simplify. |
c.
| Steps | Algebraic |
| Example | |
| Use the Quotient Property of exponents to simplify the fraction under the radical first. | |
| Rewrite the radicand using perfect fourth power factors | |
| Simplify. |
Quotient Property of Radical Expressions
If and ![]() are real numbers, b ≠ 0, and for any integer n ≥ 2 then,
are real numbers, b ≠ 0, and for any integer n ≥ 2 then,
![]()
- Simplify the fraction in the radicand, if possible.
- Use the Quotient Property to rewrite the radical as the quotient of two radicals.
- Simplify the radicals in the numerator and the denominator.
Try it! – How to Simplify the Quotient of Radical Expressions
| Steps | Explanation | Algebraic |
| Step 1. Simplify the fraction in the radicand, if possible. |
|
|
| Step 2. Use the Quotient Property to rewrite the radicals as the quotient of two radicals. | We rewrite
|
|
| Step 3. Simplify the radicals in the numerator and enumerator. |
|
2. Simplify: a. ![]() b.
b. ![]()
a.
| Steps | Algebraic |
| Example | |
| Neither radicand is a perfect cube, so use the Quotient Property to write as one radical. | |
| Simplify the fraction under the radical. | |
| Rewrite the radicand as a product using perfect cube factors. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
b.
| Steps | Algebraic |
| Example | |
| Neither radicand is a perfect cube, so use the Quotient Property to write as one radical. | |
| Simplify the fraction under the radical. | |
| Rewrite the radicand as a product using perfect fourth power factors. | |
| Rewrite the radical as the product of two radicals. | |
| Simplify. |
Simplify Expressions with 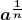
Rational exponents are another way of writing expressions with radicals. When we use rational exponents, we can apply the properties of exponents to simplify expressions.
The Power Property for Exponents says that ![]() when m and n are whole numbers. Let’s assume we are now not limited to whole numbers.
when m and n are whole numbers. Let’s assume we are now not limited to whole numbers.
Suppose we want to find a number p such that ![]() . We will use the Power Property of Exponents to find the value of p.
. We will use the Power Property of Exponents to find the value of p.
| Steps | Algebraic |
| Example | |
| Multiply the exponents on the left. | |
| Write the exponent 1 on the right | |
| Since the bases are the same, the exponents must be equal. | |
| Solve for p. |
So ![]() . But we know also
. But we know also ![]() . Then it must be that
. Then it must be that ![]() .
.
This same logic can be used for any positive integer exponent n to show that ![]() .
.
Rational Exponent 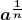
If ![]() is a real number and n ≥ 2, then
is a real number and n ≥ 2, then
![]()
The denominator of the rational exponent is the index of the radical.
There will be times when working with expressions will be easier if you use rational exponents and times when it will be easier if you use radicals. In the first few examples, you’ll practice converting expressions between these two notations.
Try it!
1. Write as a radical expression: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
We want to write each expression in the form ![]()
a.
| Steps | Algebraic |
| Expression | |
| The denominator of the rational exponent is 2, sothe index of the radical is 2. We do not show theindex when it is 2. |
b.
| Steps | Algebraic |
| Expression | |
| The denominator of the exponent is 3, so the index is 3. |
c.
| Steps | Algebraic |
| Expression | |
| The denominator of the exponent is 4, so the index is 4. |
2. Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
a.
| Steps | Algebraic |
| Expression | |
| Rewrite as square root. | |
| Simplify. |
b.
| Steps | Algebraic |
| Expression | |
| Rewrite as a cube root. | |
| Recognize 64 is a perfect cube. | |
| Simplify. |
c.
| Steps | Algebraic |
| Expression | |
| Rewrite as a fourth root. | |
| Recognize 256 is a perfect fourth power. | |
| Simplify. |
Be careful of the placement of the negative signs in the next example. We will need to use the property ![]() in one case.
in one case.
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
a.
| Steps | Algebraic |
| Expression | |
| Rewrite as a fourth root. | |
| Simplify. | No real solution. |
b.
| Steps | Algebraic |
| Expression | |
| The exponent only applies to the 16.
Rewrite as a fourth root. |
|
| Rewrite 16 as 24. | |
| Simplify. |
c.
| Steps | Algebraic |
| Expression | |
| Rewrite using the property |
|
| Rewrite as a fourth root. | |
| Rewrite 16 as 24. | |
| Simplify. |
Simplify Expressions with 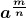
We can look at ![]() in two ways. Remember, the Power Property tells us to multiply the exponents and so
in two ways. Remember, the Power Property tells us to multiply the exponents and so ![]() and
and ![]() both equal
both equal ![]() . If we write these expressions in radical form, we get
. If we write these expressions in radical form, we get
![]()
This leads us to the following definition.
Rational Exponent 
For any positive integers m and n,
![]()
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
We will rewrite the expression as a radical first using the definition, ![]() . This form lets us take the root first and so we keep the numbers in the radicand smaller than if we used the other form.
. This form lets us take the root first and so we keep the numbers in the radicand smaller than if we used the other form.
a.
| Steps | Algebraic |
| Expression | |
| The power of the radical is the numerator of the exponent, 2.
The index of the radical is the denominator of the exponent, 3. |
|
| Simplify. | |
b. We will rewrite each expression first using ![]() and then change to radical form.
and then change to radical form.
| Rewrite using |
|
| Change to radical form. The power of the radical is the numerator of the exponent, 3. The index is the denominator of the exponent, 2. | |
| Simplify. | |
c.
| Steps | Algebraic |
| Rewrite using |
|
| Change to radical form. | |
| Rewrite the radicand as a power | ![Rendered by QuickLaTeX.com \displaystyle \frac{1}{\left(\sqrt[5]{2^5}\right)^2}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1bb00f4c70ce0d0c6305c7218036c966_l3.png) |
| Simplify. | |
Use the Properties of Exponents to Simplify Expressions with Rational Exponents
The same properties of exponents that we have already used also apply to rational exponents. We will list the Properties of Exponents here to have them for reference as we simplify expressions.
Properties of Exponents
If a and b are real numbers and m and n are rational numbers, then
| Properties | Definitions |
| Product Property | |
| Power Property | |
| Product to a Power Property | |
| Quotient Property | |
| Zero Exponent Property | |
| Quotient to a Power Property | |
| Negative Exponent Property |
We will apply these properties in the next example.
Try it!
Simplify: a. ![]() b.
b. ![]() c.
c. ![]()
Solution:
a. The Product Property tells us that when we multiply the same base, we add the exponents.
| Steps | Algebraic |
| Example | |
| The bases are the same, so we add the exponents. | |
| Add the fractions. | |
| Simplify the exponent. |
b. The Power Property tells us that when we raise a power to a power, we multiply the exponents.
| Steps | Algebraic |
| Example | |
| To raise a power to a power, we multiply the exponents. | |
| Simplify. |
c. The Quotient Property tells us that when we divide with the same base, we subtract the exponents.
| Steps | Algebraic |
| Example | |
| To divide with the same base, we subtract the exponents. | |
| Simplify. |
Access these online resources for additional instruction and practice with simplifying rational exponents.
Key Concepts
- Square Root Notation
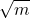 is read ‘the square root of m’
is read ‘the square root of m’- If
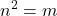 , then
, then 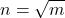 , for n ≥ 0.
, for n ≥ 0.
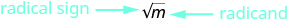
- The square root of m,
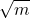 , is a positive number whose square is m.
, is a positive number whose square is m. - Simplified Square Root
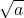 is considered simplified if a has no perfect-square factors.
is considered simplified if a has no perfect-square factors.
- Product Property of Square Roots If a, b are non-negative real numbers, then
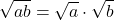
- Simplify a Square Root Using the Product Property To simplify a square root using the Product Property:
- Find the largest perfect square factor of the radicand. Rewrite the radicand as a product using the perfect square factor.
- Use the product rule to rewrite the radical as the product of two radicals.
- Simplify the square root of the perfect square.
- Quotient Property of Square Roots If a, b are non-negative real numbers and b ≠ 0, then
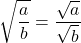
- Simplify a Square Root Using the Quotient Property To simplify a square root using the Quotient Property:
- Simplify the fraction in the radicand, if possible.
- Use the Quotient Rule to rewrite the radical as the quotient of two radicals.
- Simplify the radicals in the numerator and the denominator.
- nth Root of a Number
- If bn = a, then b is an nth root of a.
- The principal nth root of a is written
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) .
. - n is called the index of the radical.
- Properties of
![Rendered by QuickLaTeX.com \displaystyle \boldsymbol{\sqrt[n]{a}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d810b1c6a1c69af13c1748cd0c5195ef_l3.png)
- When n is an even number and
- a ≥ 0, then
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) is a real number
is a real number - a < 0, then
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) is not a real number
is not a real number
- a ≥ 0, then
- When n is an odd number,
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) is a real number for all values of a.
is a real number for all values of a.
- When n is an even number and
- Simplifying Odd and Even Roots
- For any integer n ≥ 2,
- when n is odd
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a} = a](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a8977e1fe675fe21feeb4c5b1806686a_l3.png)
- when n is even
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a} = |a|](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-18dfd41f6c2fce288e989a66acac8bec_l3.png)
- when n is odd
- We must use the absolute value signs when we take an even root of an expression with a variable in the radical.
- For any integer n ≥ 2,
- Simplified Radical Expression
- For real numbers a, m and n ≥ 2
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) is considered simplified if a has no factors of mn
is considered simplified if a has no factors of mn
- For real numbers a, m and n ≥ 2
- Product Property of nth Roots
- For any real numbers,
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) and
and ![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{b}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6abde419f6338ada5958e7564f3fb0b3_l3.png) and for any integer n ≥ 2
and for any integer n ≥ 2
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{ab} = \sqrt[n]{a}\cdot \sqrt[n]{b}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4cdd53df23b91f3bc2493efcec1920d3_l3.png) and
and ![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}\cdot \sqrt[n]{b} = \sqrt[n]{ab}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-52ea796a1db33cb9c6a9acc80e7d0eb4_l3.png)
- For any real numbers,
- How to simplify a radical expression using the Product Property
- Find the largest factor in the radicand that is a perfect power of the index.
Rewrite the radicand as a product of two factors, using that factor. - Use the product rule to rewrite the radical as the product of two radicals.
- Simplify the root of the perfect power.
- Find the largest factor in the radicand that is a perfect power of the index.
- Quotient Property of Radical Expressions
- If
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) and
and ![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{b}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6abde419f6338ada5958e7564f3fb0b3_l3.png) are real numbers, b ≠ 0, and for any integer n ≥ 2 then,
are real numbers, b ≠ 0, and for any integer n ≥ 2 then,
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-09d36d33f92f0f0f7c30e621f7196e7f_l3.png) and
and ![Rendered by QuickLaTeX.com \displaystyle \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4185044406c2258d6673b01a0fd143da_l3.png)
- If
- How to simplify a radical expression using the Quotient Property.
- Simplify the fraction in the radicand, if possible.
- Use the Quotient Property to rewrite the radical as the quotient of two radicals.
- Simplify the radicals in the numerator and the denominator.
- Rational Exponent
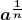
- If
![Rendered by QuickLaTeX.com \displaystyle \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d74057e47af4d348442b579fdaec3170_l3.png) is a real number and n ≥ 2, then
is a real number and n ≥ 2, then ![Rendered by QuickLaTeX.com \displaystyle a^{\frac{1}{n}} = \sqrt[n]{a}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e1ce8540e9f104f1759b4aac15f9ce54_l3.png) .
.
- If
- Rational Exponent
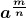
- For any positive integers m and n,
![Rendered by QuickLaTeX.com \displaystyle a^{\frac{m}{n}} = (\sqrt[n]{a})^m](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cd915a611b6a3135f5ef717a14df2325_l3.png) and
and ![Rendered by QuickLaTeX.com \displaystyle a^{\frac{m}{n}} = \sqrt[n]{a^m}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2d42fb5a23791bc191ff6aae16f11188_l3.png)
- For any positive integers m and n,
- Properties of Exponents
- If a, b are real numbers and m, n are rational numbers, then
- Product Property:
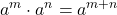
- Power Property:
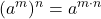
- Product to a Power Property:
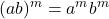
- Quotient Property:
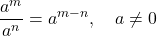
- Zero Exponent Definition:
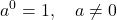
- Quotient to a Power Property:
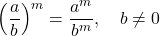
- Negative Exponent Property:
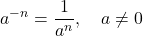
- Product Property:
- If a, b are real numbers and m, n are rational numbers, then

