3 Fractions, Decimals, Percents
Topics Covered:
Fraction Basics[1]
A fraction is a way to represent parts of a whole. The fraction ![]() represents two of three equal parts. In the fraction
represents two of three equal parts. In the fraction ![]() , the 2 is called the numerator and the 3 is called the denominator. The line is called the fraction bar.
, the 2 is called the numerator and the 3 is called the denominator. The line is called the fraction bar.
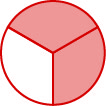
 of the circle is shaded – 2 of the 3 equal parts.
of the circle is shaded – 2 of the 3 equal parts.A fraction is written ![]() , where b ≠ 0 and
, where b ≠ 0 and
a is the numerator and b is the denominator.
A fraction represents parts of a whole. The denominator b is the number of equal parts the whole has been divided into, and the numerator a indicates how many parts are included.
Fractions that have the same value are equivalent fractions.
The Equivalent Fractions Property allows us to find equivalent fractions and also simplify fractions.
If a, b, and c are numbers where b ≠ 0, c ≠ 0,
then ![]() =
= ![]() and
and ![]()
A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator.
For example,
![]() is simplified because there are no common factors of 2 and 3.
is simplified because there are no common factors of 2 and 3.
![]() is not simplified because 5 is a common factor of 10 and 15.
is not simplified because 5 is a common factor of 10 and 15.
We simplify, or reduce, a fraction by removing the common factors of the numerator and denominator. A fraction is not simplified until all common factors have been removed. If an expression has fractions, it is not completely simplified until the fractions are simplified.
Sometimes it may not be easy to find common factors of the numerator and denominator. When this happens, a good idea is to factor the numerator and the denominator into prime numbers. Then divide out the common factors using the Equivalent Fractions Property.
Try it!
- Simplify:
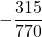
Solution
Solution (click to reveal)



2. Simplify: ![]()
Solution
Solution (click to reveal)
![]()
We now summarize the steps you should follow to simplify fractions.
How to simplify a fraction.
- Rewrite the numerator and denominator to show the common factors.
If needed, factor the numerator and denominator into prime numbers first. - Simplify using the Equivalent Fractions Property by dividing out common factors.
- Multiply any remaining factors.
Multiply and Divide Fractions[2]
Many people find multiplying and dividing fractions easier than adding and subtracting fractions.
To multiply fractions, we multiply the numerators and multiply the denominators.
Fraction Multiplication
If a, b, c, and d are numbers where b ≠ 0, and d ≠ 0, then:
![]()
To multiply fractions, multiply the numerators and multiply the denominators.
When multiplying fractions, the properties of positive and negative numbers still apply, of course. It is a good idea to determine the sign of the product as the first step. In the next example, we will multiply a negative and a positive, so the product will be negative.
When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, a, can be written as ![]() . So, for example,
. So, for example, ![]() .
.
Try it!
- Multiply:
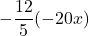
Solution
Solution (click to reveal)
The first step is to find the sign of the product. Since the signs are the same, the product is positive.
| Steps | Algebraic |
| Example | |
| Determine the sign of the product. The signs are the same, so the product is positive.. | |
| Write 20x as a fraction. | |
| Multiply. | |
| Rewrite 20 to show the common factor 5 and divide it out. | |
| Simplify. |
2. Multiply: ![]()
Solution
Solution (click to reveal)
−33a
3. Multiply: ![]()
Solution
Solution (click to reveal)
Now that we know how to multiply fractions, we are almost ready to divide. Before we can do that, we need some vocabulary. The reciprocal of a fraction is found by inverting the fraction, placing the numerator in the denominator and the denominator in the numerator. The reciprocal of ![]() is
is ![]() . Since 4 is written in fraction form as
. Since 4 is written in fraction form as ![]() , the reciprocal of 4 is
, the reciprocal of 4 is ![]() .
.
To divide fractions, we multiply the first fraction by the reciprocal of the second.
Fraction Division
If a, b, c, and d are numbers where b ≠ 0, c ≠ 0, and d ≠ 0, then
![]()
To divide fractions, we multiply the first fraction by the reciprocal of the second.
We need to say b ≠ 0, c ≠ 0, and d ≠ 0, to be sure we don’t divide by zero!
Try it!
- Find the quotient:
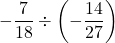
Solution
Solution (click to reveal)
| Steps | Algebraic |
| Example | |
| To divide, multiply the first fraction by the reciprocal of the second. | |
| Determine the sign of the product, and then multiply. |
|
| Rewrite showing common factors. | |
| Remove common factors. | |
| Simplify. |
2. Divide: ![]()
Solution
Solution (click to reveal)
3. Divide: ![]()
Solution
Solution (click to reveal)
The numerators or denominators of some fractions contain fractions themselves. A fraction in which the numerator or the denominator is a fraction is called a complex fraction.
A complex fraction is a fraction in which the numerator or the denominator contains a fraction.
Some examples of complex fractions are:
![]()
To simplify a complex fraction, remember that the fraction bar means division. For example, the complex fraction ![]() means
means ![]() .
.
Try it!
- Simplify:
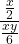
Solution
Solution (click to reveal)
| Steps | Algebraic |
| Example | |
| Rewrite as division. | |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Look for common factors. | |
| Divide common factors and simplify. |
Solution
Solution (click to reveal)
![]()
Add and Subtract Fractions[3]
When we multiplied fractions, we just multiplied the numerators and multiplied the denominators right straight across. To add or subtract fractions, they must have a common denominator.
Fraction Addition and Subtraction
If a, b, and c are numbers where c ≠ 0, then
![]()
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
The least common denominator (LCD) of two fractions is the smallest number that can be used as a common denominator of the fractions. The LCD of the two fractions is the least common multiple (LCM) of their denominators.
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
After we find the least common denominator of two fractions, we convert the fractions to equivalent fractions with the LCD. Putting these steps together allows us to add and subtract fractions because their denominators will be the same!
Try it!
- Add:
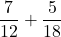
Solution



Solution
![]()
Solution
How to add or subtract fractions.
- Do they have a common denominator?
- Yes—go to step 2.
- No—rewrite each fraction with the LCD (least common denominator).
- Find the LCD.
- Change each fraction into an equivalent fraction with the LCD as its denominator.
- Add or subtract the fractions.
- Simplify, if possible.
We now have all four operations for fractions. The table summarizes fraction operations.
| Fraction Multiplication | Fraction Division |
|---|---|
| Multiply the numerators and multiply the denominators | Multiply the first fraction by the reciprocal of the second. |
| Fraction Addition | Fraction Subtraction |
| Add the numerators and place the sum over the common denominator. | Subtract the numerators and place the difference over the common denominator. |
| To multiply or divide fractions, an LCD is NOT needed. To add or subtract fractions, an LCD is needed. |
|
When starting an exercise, always identify the operation and then recall the methods needed for that operation.
Try it!
- Simplify: a.
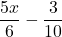 b.
b. 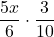
First ask, “What is the operation?” Identifying the operation will determine whether or not we need a common denominator. Remember, we need a common denominator to add or subtract, but not to multiply or divide.
a.
| Steps | Algebraic |
| What is the operation? | The operation is subtraction. |
| Do the fractions have a common denominator? No. | |
| Find the LCD of 6 and 10
6 = 2 • 3 10 = 2 • 5 LCD = 2 • 3 • 5 LCD = 30 |
The LCD is 30. |
| Rewrite each fraction as an equivalent fraction with the LCD. |
|
| Subtract the numerators and place the difference over the common denominators. | |
| Simplify, if possible. | There are no common factors. The fraction is simplified. |
b.
| Steps | Algebraic |
| What is the operation? Multiplication | |
| To multiply fractions, multiply the numerators and multiply the denominators. | |
| Rewrite, showing common factors & Remove common factors. | 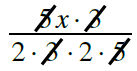 |
| Simplify |
Notice, we needed an LCD to add in the first exercise, but not to multiply in the second.
2. Simplify: a. ![]() b.
b. ![]()
3. Simplify: a. ![]() b.
b. ![]()
Decimal Basics[4]
To add or subtract decimals, we line up the decimal points. By lining up the decimal points this way, we can add or subtract the corresponding place values. We then add or subtract the numbers as if they were whole numbers and then place the decimal point in the sum.
How to add or subtract decimals.
- Determine the sign of the sum or difference.
- Write the numbers so the decimal points line up vertically.
- Use zeros as placeholders, as needed.
- Add or subtract the numbers as if they were whole numbers. Then place the decimal point in the answer under the decimal points in the given numbers.
- Write the sum or difference with the appropriate sign.
Try it!
Add or subtract: a. ![]() b.
b. ![]()
Solution
a. ![]()
| Steps |
Algebraic |
| The difference will be negative. To subtract, we add the numerals. Write the numbers so the decimal points line up vertically. |
23.5 + 41.38 |
| Put 0 as a placeholder after the 5 in 23.5. Remember, |
23.50 + 41.38 |
| Add the numbers as if they were whole numbers. Then place the decimal point in the sum. | |
| Write the result with the correct sign. |
b. ![]()
| Steps |
Algebraic |
| The difference will be negative. To subtract, we subtract 14.65 from 20. Write the numbers so the decimal points line up vertically. |
20 – 14.65 |
| Remember, 20 is a whole number, so place the decimal point after the 0. Put in zeros to the right as placeholders. |
20.00 – 14.65 |
| Subtract and place the decimal point in the answer. | 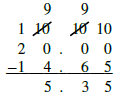 |
| Write the result with the correct sign. |
When we multiply signed decimals, first we determine the sign of the product and then multiply as if the numbers were both positive. We multiply the numbers temporarily ignoring the decimal point and then count the number of decimal points in the factors and that sum tells us the number of decimal places in the product. Finally, we write the product with the appropriate sign.
How to multiply decimals.
- Determine the sign of the product.
- Write in vertical format, lining up the numbers on the right. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors.
- Write the product with the appropriate sign.
Try it!
Multiply: ![]()
Solution
| Steps | Algebraic |
| Example | |
| The signs are different. The product will be negative. |
The product will be negative. |
| Write in vertical format, lining up the numbers on the right. |
|
| Multiply. |  |
| Add the number of decimal places in the factors (1 + 3). Place the decimal point 4 places from the right. |
 |
| The signs are different, so the product is negative. |
Often, especially in the sciences, you will multiply decimals by powers of 10 (10, 100, 1000, etc). If you multiply a few products on paper, you may notice a pattern relating the number of zeros in the power of 10 to number of decimal places we move the decimal point to the right to get the product.
How to multiply a decimal by a power of ten.
- Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
- Add zeros at the end of the number as needed.
Try it!
Multiply: 5.63 by a. 10 b. 100 c. 1000.
Solution
By looking at the number of zeros in the multiple of ten, we see the number of places we need to move the decimal to the right.
a.
| Steps | Algebraic |
| Example | 5.63 (10) |
| There is 1 zero in 10, so move the decimal point 1 place to the right. | |
| Solution | 56.3 |
b.
| Steps | Algebraic |
| Example | 5.63 (100) |
| There are 2 zeroes in 100, so move the decimal point 2 places to the right. | |
| Solution | 563 |
c.
| Steps | Algebraic |
| Example | 5.63 (1000) |
| There are 3 zeroes in 1,000, so move the decimal point 3 place to the right. | |
| A zero must be added to the end. | 5630 |
Just as with multiplication, division of signed decimals is very much like dividing whole numbers. We just have to figure out where the decimal point must be placed and the sign of the quotient. When dividing signed decimals, first determine the sign of the quotient and then divide as if the numbers were both positive. Finally, write the quotient with the appropriate sign.
We review the notation and vocabulary for division:

We’ll write the steps to take when dividing decimals for easy reference.
How to divide decimals.
- Determine the sign of the quotient.
- Make the divisor a whole number by “moving” the decimal point all the way to the right. “Move” the decimal point in the dividend the same number of places—adding zeros as needed.
- Divide. Place the decimal point in the quotient above the decimal point in the dividend.
- Write the quotient with the appropriate sign.
Try it!
Divide: ![]() .
.
Solution
Remember, you can “move” the decimals in the divisor and dividend because of the Equivalent Fractions Property.
| Steps | Algebraic |
| The signs are the same. | The quotient is positive. |
| Make the divisor a whole number by “moving” the decimal point all the way to the right. | |
| “Move” the decimal point in the dividend the same number of places. |
|
| Divide.
Place the decimal point in the quotient above the |
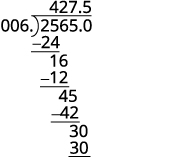 |
| Write the quotient with the appropriate sign. | |
Percent Basics[5]
How many cents are in one dollar? There are 100 cents in a dollar. How many years are in a century? There are 100 years in a century. Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is 100. We use the percent symbol %, to show percent.
A percent is a ratio whose denominator is 100.
According to data from the American Association of Community Colleges (2015), about 57% of community college students are female. This means 57 out of every 100 community college students are female, as the image below shows. Out of the 100 squares on the grid, 57 are shaded, which we write as the ratio ![]() .
.

Similarly, 25% means a ratio of ![]() , 3% means a ratio of
, 3% means a ratio of ![]() , and 100% means a ratio of
, and 100% means a ratio of ![]() . In words, “one hundred percent” means the total 100% is
. In words, “one hundred percent” means the total 100% is ![]() , and since
, and since ![]() , we see that 100% means 1 whole.
, we see that 100% means 1 whole.
Try it!
- According to the Public Policy Institute of California (2010), 44% of parents of public school children would like their youngest child to earn a graduate degree. Write this percent as a ratio.
| Steps | Algebraic |
| The amount we want to convert is 44%. | 44% |
| Write the percent as a ratio. Remember that percent means per 100. |
2. In 2007, according to a U.S. Department of Education report, 21 out of every 100 first-time freshmen college students at 4-year public institutions took at least one remedial course. Write this as a ratio and then as a percent.
| Steps | Algebraic |
| The amount we want to convert is 21 out of 100. | 21 out of 100 |
| Write as a ratio. | |
| Convert the 21 per 100 to percent. | 21% |
Since percents are ratios, they can easily be expressed as fractions. Remember that percent means per 100, so the denominator of the fraction is 100.
How to convert a percent to a fraction.
- Write the percent as a ratio with the denominator 100.
- Simplify the fraction if possible.
Try it!
Convert each percent to a fraction: a. 36% b. 125%
Solution
a.
| Steps | Algebraic |
| Percentage | 36% |
| Write as a ratio with denominator 100. | |
| Simplify. |
b.
| Steps | Algebraic |
| Percentage | 125% |
| Write as a ratio with denominator 100. | |
| Simplify. |
The previous example shows that a percent can be greater than 1. We saw that 125% means ![]() , or
, or ![]() . These are improper fractions, and their values are greater than one.
. These are improper fractions, and their values are greater than one.
Try it!
Convert each percent to a fraction: a. 24.5% b. ![]() %
%
| Steps | Algebraic |
| Percentage | 24.5% |
| Write as a ratio with denominator 100. | |
| Clear the decimal by multiplying numerator and denominator by 10. | |
| Multiply. | |
| Rewrite showing common factors. | |
| Simplify. |
b.
| Steps | Algebraic |
| Percentage | |
| Write as a ratio with denominator 100. | |
| Write the numerator as an improper fraction. | |
| Rewrite as fraction division, replacing 100 with |
|
| Multiply by the reciprocal. | |
| Simplify. |
In decimals, we learned how to convert fractions to decimals. To convert a percent to a decimal, we first convert it to a fraction and then change the fraction to a decimal.
How to convert a percent to a decimal.
- Write the percent as a ratio with the denominator 100.
- Convert the fraction to a decimal by dividing the numerator by the denominator.
Try it!
- Convert each percent to a decimal: a. 6% b. 78%
Solution
Because we want to change to a decimal, we will leave the fractions with denominator 100 instead of removing common factors.
a.
| Steps | Algebraic |
| Percentage | 6% |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.06 |
b.
| Steps | Algebraic |
| Percentage | 78% |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.78 |
2. Convert each percent to a decimal: a. 135%b. 12.5%
Solution
a.
| Steps | Algebraic |
| Percentage | 135% |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 1.35 |
b.
| Steps | Algebraic |
| Percentage | 12.5% |
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.125 |
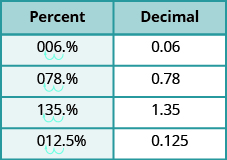
Let’s summarize the results from the previous examples in the table, and look for a pattern we could use to quickly convert a percent number to a decimal number.
| Percent | Decimal |
|---|---|
| 6% | 0.06 |
| 78% | 0.78 |
| 135% | 1.35 |
| 12.5% | 0.125 |
Do you see the pattern?
To convert a percent number to a decimal number, we move the decimal point two places to the left and remove the % sign. (Sometimes the decimal point does not appear in the percent number, but just like we can think of the integer 6 as 6.0, we can think of 6% as 6.0%.) Notice that we may need to add zeros in front of the number when moving the decimal to the left.
The table below uses the percents from the table above and shows visually how to convert them to decimals by moving the decimal point two places to the left.
Try it!
- Among a group of business leaders, 77% believe that poor math and science education in the U.S. will lead to higher unemployment rates.
Convert the percent to: a. a fraction b. a decimal
Solution
a.
| Steps | Algebraic |
| Percentage | 77% |
| Write as a ratio with denominator 100. |
b.
| Steps | Algebraic |
| Percentage | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.77 |
2. There are four suits of cards in a deck of cards—hearts, diamonds, clubs, and spades. The probability of randomly choosing a heart from a shuffled deck of cards is 25%.
Convert the percent to: a. a fraction b. a decimal
Solution
a.
| Steps | Algebraic |
| Percentage | 25% |
| Write as a ratio with denominator 100. | |
| Simplify. |
b.
| Steps | Algebraic |
| Percentage | |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.25 |
Key Concepts
- Equivalent Fractions Property
If a, b, and c are numbers where b ≠ 0, c ≠ 0, then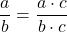 and
and 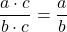
- How to simplify a fraction.
- Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers first.
- Simplify using the Equivalent Fractions Property by dividing out common factors.
- Multiply any remaining factors.
- Fraction Multiplication
If a, b, c, and d are numbers where b ≠ 0, and d ≠ 0, then:
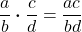
To multiply fractions, multiply the numerators and multiply the denominators.
- Fraction Division
If a, b, c, and d are numbers where b ≠ 0, c ≠ 0, and d ≠ 0, then
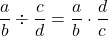
To divide fractions, we multiply the first fraction by the reciprocal of the second.
- Fraction Addition and Subtraction
If a, b, and c are numbers where c ≠ 0, then
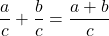 and
and 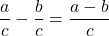
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
- Placement of Negative Sign in a Fraction
For any positive numbers a and b,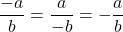
- How to simplify complex fractions.
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator. Simplify if possible.
- Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
- Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
- Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
- Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
- Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction ↵

