29 Properties of Logarithms
Topics Covered
Now that we have learned about exponential and logarithmic functions, we can introduce some of the properties of logarithms. These will be very helpful as we continue to solve both exponential and logarithmic equations. In the previous section we already introduced Basic property and inverse property, which we will review below.
Properties of Logarithms
The first two properties derive from the definition of logarithms. Since a0 = 1, we can convert this to logarithmic form and get ![]() . Also, since a1 = a, we get
. Also, since a1 = a, we get ![]() .
.
![]()
Inverse Properties of Logarithms
These two properties are called inverse properties because, when we have the same base, raising to a power “undoes” the log and taking the log “undoes” raising to a power. These two properties show the composition of functions. Both ended up with the identity function which shows again that the exponential and logarithmic functions are inverse functions.
For a > 0, x > 0 and a ≠ 1,
![]()
Use the Properties of Logarithms
Recall that the logarithmic and exponential functions “undo” each other. This means that logarithms have similar properties to exponents. Our definition of logarithm shows us that a logarithm is the exponent of the equivalent exponential function. The properties of exponents have related properties for logarithms. There are three more properties of logarithms that will be useful in our work.
Before we can solve an equation like ![]() , we need a method for combining terms on the left side of the equation.
, we need a method for combining terms on the left side of the equation.
Recall that we use the Product Property of Exponents, am · an = am+n, we see that to multiply the same base, we add the exponents. We have a similar property for logarithms, called the Product Property of Logarithms, which tells us that to take the log of a product, we add the log of the factors. Because logs are exponents, and we multiply like bases, we can add the exponents.
Product Property of Logarithms
If M > 0, N > 0, a > 0 and a ≠ 1, then,
![]()
The logarithm of a product is the sum of the logarithms.
We use this property to write the log of a product as a sum of the logs of each factor.
Given the logarithm of a product, use the product rule of logarithms to write an equivalent sum of logarithms.
- Factor the argument completely, expressing each whole number factor as a product of primes.
- Write the equivalent expression by summing the logarithms of each factor.
Try it!
1. Use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify, if possible:
![]()
Solution:
a)
| Steps | Algebraic |
| Use the Product Property, |
|
b)
| Steps | Algebraic |
| Use the Product Property, |
|
2. Use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify, if possible.
![]()
Solution:
a) ![]()
b) ![]()
Try it! – Using the Product Rule for Logarithms
Expand ![]() .
.
Solution:
We begin by factoring the argument completely, expressing 30 as a product of primes.
![]()
Next, we write the equivalent equation by summing the logarithms of each factor.
![]()
Quotient Property
Similarly, in the Quotient Property of Exponents, ![]() , we see that to divide the same base, we subtract the exponents. The Quotient Property of Logarithms,
, we see that to divide the same base, we subtract the exponents. The Quotient Property of Logarithms, ![]() tells us to take the log of a quotient, we subtract the log of the numerator and denominator.
tells us to take the log of a quotient, we subtract the log of the numerator and denominator.
Quotient Property of Logarithms
If M > 0, N > 0, a > 0 and a ≠ 1, then,
![]()
The logarithm of a quotient is the difference of the logarithms.
We use this property to write the log of a quotient as the difference of the logs of each factor.
Given the logarithm of a quotient, use the quotient rule of logarithms to write an equivalent difference of logarithms.
- Express the argument in lowest terms by factoring the numerator and denominator and canceling common terms.
- Write the equivalent expression by subtracting the logarithm of the denominator from the logarithm of the numerator.
- Check to see that each term is fully expanded. If not, apply the product rule for logarithms to expand completely.
Try it!
1. Use the Quotient Property of Logarithms to write each logarithm as a difference of logarithms. Simplify, if possible.
![]() .
.
Solution:
a)
| Steps | Algebraic |
| Use the Quotient Property, |
|
b)
| Steps | Algebraic |
| Use the Quotient Property, |
|
2. Use the Quotient Property of Logarithms to write each logarithm as a difference of logarithms. Simplify, if possible.
![]() .
.
Solution:
a) ![]() and
and
b) ![]()
3. Use the Quotient Property of Logarithms to write each logarithm as a difference of logarithms. Simplify, if possible.
![]() .
.
Solution:
a) ![]() and
and
b) ![]()
Try it! – Using the Quotient Rule for Logarithms
Expand ![]() .
.
Solution:
First, we note that the quotient is factored and in lowest terms, so we apply the quotient rule.
![]()
Notice that the resulting terms are logarithms of products. To expand completely, we apply the product rule, noting that the prime factors of the factor 15 are 3 and 5.
![Rendered by QuickLaTeX.com \begin{align*} \log_2(15x(x - 1)) - \log_2((3x + 4)(2 - x)) &= [\log_2(3) + \log_2(5) + \log_2(x) + \log_2(x -1)] \\ & \quad - [\log_2(3x + 4) + \log_2(2 - x)] \\[0.15cm] &= \log_2(3) + \log_2(5) + \log_2(x) + \log_2(x - 1) \\ &\quad - \log_2(3x + 4) - \log_2 (2 -x)\end{align*}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7e9125a0757ba767dbed9d6775537d64_l3.png)
Analysis:
There are exceptions to consider in this and later examples. First, because denominators must never be zero, this expression is not defined for ![]() and
and ![]() . Also, since the argument of a logarithm must be positive, we note as we observe the expanded logarithm, that
. Also, since the argument of a logarithm must be positive, we note as we observe the expanded logarithm, that ![]() , and
, and ![]() . Combining these conditions is beyond the scope of this section, and we will not consider them here or in subsequent exercises.
. Combining these conditions is beyond the scope of this section, and we will not consider them here or in subsequent exercises.
Power Property
We’ve explored the product rule and the quotient rule, but how can we take the logarithm of a power, such as x2? The third property of logarithms is related to the Power Property of Exponents, (am)n = am·n, we see that to raise a power to a power, we multiply the exponents.
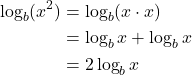
Notice that we used the product property for logarithms to find a solution for the example above. By doing so, we have derived the Power Property of Logarithms, ![]() , which tells us to take the log of a number raised to a power, we multiply the power times the log of the number.
, which tells us to take the log of a number raised to a power, we multiply the power times the log of the number.
Power Property of Logarithms
If M > 0, N > 0, a > 0 and a ≠ 1, and p is any real number then,
![]()
We use this property to write the log of a number raised to a power as the product of the power times the log of the number. We essentially take the exponent and throw it in front of the logarithm.
Try it!
1. Use the Power Property of Logarithms to write each logarithm as a product of logarithms. Simplify, if possible.
![]() .
.
Solution:
a)
| Steps | Algebraic |
| Use the Power Property, |
|
b)
| Steps | Algebraic |
| Use the Power Property, |
|
2. Use the Power Property of Logarithms to write each logarithm as a product of logarithms. Simplify, if possible.
![]() .
.
Solution:
a) ![]() b)
b) ![]()
Expand and Condense Logarithms
We summarize the Properties of Logarithms here for easy reference. While the natural logarithms are a special case of these properties, it is often helpful to also show the natural logarithm version of each property.
If M > 0, N > 0, a > 0, a ≠ 1 and p is any real number then,
| Property | Base a | Base e |
| Inverse Properties |
|
|
| Product Property of Logarithms | ||
| Quotient Property of Logarithms | ||
| Power Property of Logarithms |
Now that we have the properties we can use them to “expand” a logarithmic expression. This means to write the logarithm as a sum or difference and without any powers.
Taken together, the product rule, quotient rule, and power rule are often called “laws of logs.” Sometimes we apply more than one rule in order to simplify an expression. For example:
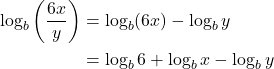
We generally apply the Product and Quotient Properties before we apply the Power Property. Remember, however, that we can only do this with products, quotients, powers, and roots—never with addition or subtraction inside the argument of the logarithm.
Try it!
1. Use the Properties of Logarithms to expand the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
| Steps | Algebraic |
| Use the Product Property, |
|
| Use the Power Property, |
|
| Simplify. | |
2. Use the Properties of Logarithms to expand the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
![]()
Try it! – Expanding Logarithms Using Product, Quotient, and Power Rules
1. Rewrite ![]() as a sum or difference of logs.
as a sum or difference of logs.
Solution:
First, because we have a quotient of two expressions, we can use the quotient rule:
![]()
Then seeing the product in the first term, we use the product rule:
![]()
Finally, we use the power rule on the first term:
![]()
2. Expand ![]()
Solution:
![]()
Try it! – Expanding Complex Logarithmic Expressions
Expand ![]() .
.
Solution:
We can expand by applying the Product and Quotient Rules.
| Steps | Algebraic |
| Apply the Quotient Rule. | |
| Simplify by writing 64 as 26. | |
| Apply the Power Rule. |
When we have a radical in the logarithmic expression, it is helpful to first write its radicand as a rational exponent.
Try it! – Using the Power Rule for Logarithms to Simplify the Logarithm of a Radical Expression
1. Expand ![]() .
.
Solution:
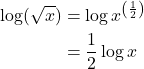
2. Use the Properties of Logarithms to expand the logarithm ![Rendered by QuickLaTeX.com \displaystyle \log_2\sqrt[4]{\frac{x^3}{3y^2 z}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b1d020bd7c12722bea4876b8cf9d82a0_l3.png) . Simplify, if possible.
. Simplify, if possible.
Solution:
| Steps | Algebraic |
![Rendered by QuickLaTeX.com \displaystyle \log_2\sqrt[4]{\frac{x^3}{3y^2 z}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b1d020bd7c12722bea4876b8cf9d82a0_l3.png) |
|
| Rewrite the radical with a rational exponent. | 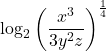 |
| Use the Power Property,
|
|
| Use the Quotient Property, |
|
| Use the Product Property,
|
|
| Use the Power Property,
|
|
| Simplify by distributing. | |
![Rendered by QuickLaTeX.com \displaystyle \log_2\sqrt[4]{\frac{x^3}{3y^2 z}} = \frac{1}{4}\big(3\log_2 x- \log_2 3 - 2\log_2 y - \log_2 z\big)](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bc8f1623b93eb1a7fd26b96031df028d_l3.png) |
3. Use the Properties of Logarithms to expand the logarithm ![Rendered by QuickLaTeX.com \displaystyle \log_4\sqrt[5]{\frac{x^4}{2y^3 z^2}}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4adaaee101e42fcb9ad4a26744dc9207_l3.png) . Simplify, if possible.
. Simplify, if possible.
Solution:
![]()
4. Expand ![]() .
.
Solution:
![]()
Can we expand ln(x2 + y2)?
No. There is no way to expand the logarithm of a sum or difference inside the argument of the logarithm.
Condense Logarithms
The opposite of expanding a logarithm is to condense a sum or difference of logarithms that have the same base into a single logarithm. We again use the properties of logarithms to help us, but in reverse.
To condense logarithmic expressions with the same base into one logarithm, we start by using the Power Property to get the coefficients of the log terms to be one and then the Product and Quotient Properties as needed.
Given a sum, difference, or product of logarithms with the same base, write an equivalent expression as a single logarithm.
- Apply the power property first. Identify terms that are products of factors and a logarithm, and rewrite each as the logarithm of a power.
- Next apply the product property. Rewrite sums of logarithms as the logarithm of a product.
- Apply the quotient property last. Rewrite differences of logarithms as the logarithm of a quotient.
Try it!
1. Use the Properties of Logarithms to condense the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
| Steps | Algebraic |
| The log expressions all have the same base, 4. | |
| The first two terms are added, so we use the Product Property,
|
|
| Since the logs are subtracted, we use the Quotient Property,
|
|
| |
2. Use the Properties of Logarithms to condense the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
![]()
3. Use the Properties of Logarithms to condense the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
![]()
4. Use the Properties of Logarithms to condense the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
| Steps | Algebraic |
| The log expressions have the same base, 3. | |
| Use the Power Property,
|
|
| The terms are added, so we use the ProductProperty,
|
|
5. Use the Properties of Logarithms to condense the logarithm ![]() . Simplify, if possible.
. Simplify, if possible.
Solution:
![]()
Try it! – Condensing Complex Logarithmic Expressions
Condense ![]() .
.
Solution:
We apply the power rule first:
![]()
Next, we apply the product rule to the sum:
![]()
Finally, we apply the quotient rule to the difference:
![]()
Use the Change-of-Base Formula
Most calculators can evaluate only common and natural logs. In order to evaluate logarithms with a base other than 10 or e, we use the change-of-base formula to rewrite the logarithm as the quotient of logarithms of any other base; when using a calculator, we would change them to common or natural logs. We will show how this is derived by using the one-to-one property and power rule for logarithms.
| Steps | Algebraic |
| Suppose we want to evaluate |
|
| Let |
|
| Rewrite the expression in exponential form. | |
| Take the |
|
| Use the Power Property. | |
| Solve for |
|
| Substitute |
The Change-of-Base Formulaintroduces a new base b. This can be any base b we want where b > 0, b ≠ 1. Because our calculators have keys for logarithms base 10 and base e, we will rewrite the Change-of-Base Formula with the new base as 10 or e.
Change-of-Base Formula
The change-of-base formula can be used to evaluate a logarithm with any base.
For any logarithmic bases a, b and M > 0,
| xxx | xxx | ||
|---|---|---|---|
| Formula | |||
| Base | new base b | new base 10 | new base e |
Given a logarithm with the form logbM, use the change-of-base formula to rewrite it as a quotient of logs with any positive base n, where n ≠ 1.
- Determine the new base n, remembering that the common log, log(x), has base 10, and the natural log, ln(x), has base e.
- Rewrite the log as a quotient using the change-of-base formula
- The numerator of the quotient will be a logarithm with base n and argument M.
- The denominator of the quotient will be a logarithm with base n and argument b.
Try it! – Changing Logarithmic Expressions to Expressions Involving Only Natural Logs
Change ![]() to a quotient of natural logarithms.
to a quotient of natural logarithms.
Solution:
Because we will be expressing ![]() as a quotient of natural logarithms, the new base, n = e.
as a quotient of natural logarithms, the new base, n = e.
We rewrite the log as a quotient using the change-of-base formula. The numerator of the quotient will be the natural log with argument 3. The denominator of the quotient will be the natural log with argument 5.
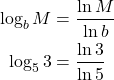
When we use a calculator to find the logarithm value, we usually round to three decimal places. This gives us an approximate value and so we use the approximately equal symbol (≈).
Try it!
Rounding to three decimal places, approximate ![]() .
.
Solution:
| Steps | Algebraic |
| Use the Change-of-Base Formula. | |
| Identify a and M. Choose 10 for b. | |
| Enter the expression |
Try it! – Using the Change-of-Base Formula with a Calculator
1. Evaluate ![]() using the change-of-base formula with a calculator.
using the change-of-base formula with a calculator.
Solution:
According to the change-of-base formula, we can rewrite the log base 2 as a logarithm of any other base. Since our calculators can evaluate the natural log, we might choose to use the natural logarithm, which is the log base e.

2. Rounding to three decimal places, approximate ![]() .
.
Solution:
3.402
Access these online resources for additional instruction and practice with using the properties of logarithms.
Solve Logarithmic Equations Using the Properties of Logarithms[1]
In the section on logarithmic functions, we solved some equations by rewriting the equation in exponential form. Now that we have the properties of logarithms, we have additional methods we can use to solve logarithmic equations.
If our equation has two logarithms we can use a property that says that if logaM=logaN then it is true that M=N. This is the One-to-One Property of Logarithmic Equations.
One-to-One Property of Logarithmic Equations
For M > 0, N > 0, a > 0, and a ≠ 1 is any real number:
If logaM = logaN, then M = N.
To use this property, we must be certain that both sides of the equation are written with the same base.
Remember that logarithms are defined only for positive real numbers. Check your results in the original equation. You may have obtained a result that gives a logarithm of zero or a negative number.
Try-it!
Solve: 2log5x=log581.
Solution
| Steps | Algebraic |
| 2log5x=log581 | |
| Use the Power Property. | log5x2=log581 |
| Use the One-to-One Property, if logaM=logaN, then M=N | x2=81 |
| Solve using the Square Root Property. | x=±9 |
| We eliminate x=-9 as we cannot take the logarithm of a negative number | x=9,x=-9 |
| Check. | |
| x=92log5x2log59log592log581==?=?=log581log581log581log581 |
Another strategy to use to solve logarithmic equations is to condense sums or differences into a single logarithm.
Try it!
Solve: log3x+log3(x-8)=2.
Solution
| Steps | Algebraic |
| log3x+log3(x-8)=2 | |
| Use the Product Property, logaM+logaN=logaM·N. | log3x(x-8)=2 |
| Rewrite in exponential form. | 32=x(x-8) |
| Simplify. | 9=x2-8x |
| Subtract 9 from each side. | 0=x2-8x-9 |
| Factor. | 0=(x-9)(x+1) |
| Use the Zero-Product Property. | x-9=0,x+1=0 |
| Solve each equation. | x=9,x=-1 |
| Check. | |
| x=-1log3x+log3(x-8)=2log3(-1)+log3(-1-8)?2 | |
| We cannot take the log of a negative number. | |
| x=9log3x+log3(x-8)=2log39+log3(9-8)=?22+0=?22=2 |
# 2 Solve: log4(x+6)-log4(2x+5)=-log4x.
Solution
| Steps | Algebraic |
| log4(x+6)-log4(2x+5)=-log4x | |
| Use the Quotient Property on the left side and the Power Property on the right. | log4(x+62x+5)=log4x-1 |
| Rewrite x-1=1x. | log4(x+62x+5)=log41x |
| Use the One-to-One Property, if logaM=logaN, then M=N. | x+62x+5=1x |
| Solve the rational equation. | x(x+6)=2x+5 |
| Distribute. | x2+6x=2x+5 |
| Write in standard form. | x2+4x-5=0 |
| Factor. | (x+5)(x-1)=0 |
| Use the Zero-Product Propriety. | x+5=0,x-1=0 |
| Solve each equation. | x=-5,x=1 |
| Check. | |
| We leave the check for you. |
Solve Exponential Equations Using Logarithms
In the section on exponential functions, we solved some equations by writing both sides of the equation with the same base. Next we wrote a new equation by setting the exponents equal.
It is not always possible or convenient to write the expressions with the same base. In that case we often take the common logarithm or natural logarithm of both sides once the exponential is isolated.
Try it!
Solve 5x=11. Find the exact number and then approximate it to three decimal places.
| Steps | Algebraic |
| 5x=11 | |
| Since the exponential is isolated, take the logarithm of both sides. Use the Power Property to get the x as a factor, not an exponent. | |
| Solve for x. Find the exact answer. | log5xxlog5xx===≈log11log11log11log51.490 |
| Approximate the answer. | |
| Since 51=5 and 52=25, does it make sense that 51.490≈11? |
Exercises
#2 Solve 3ex+2=24. Find the exact answer and then approximate it to three decimal places.
Solution
| Steps | Algebraic |
| 3ex+2=24 | |
| Isolate the exponential by dividing both sides by 3. | ex+2=8 |
| Take the natural logarithm of both sides. | lnex+2=ln8 |
| Use the Power Property to get the x as a factor, not an exponent. | (x+2)lne=ln8 |
| Use the property lne=1 to simplify. | x+2=ln8 |
| Solve the equation. Find the exact answer. | x=ln8-2 |
| Approximate the answer. | x≈0.079 |
Key Concepts
- Properties of Logarithms

- Inverse Properties of Logarithms
- For a > 0, x > 0 and a ≠ 1

- For a > 0, x > 0 and a ≠ 1
- Product Property of Logarithms
- If M > 0, N > 0, a > 0 and a ≠ 1, then,
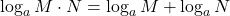
The logarithm of a product is the sum of the logarithms.
- If M > 0, N > 0, a > 0 and a ≠ 1, then,
- Quotient Property of Logarithms
- If M > 0, N > 0, a > 0 and a ≠ 1, then,
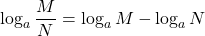
The logarithm of a quotient is the difference of the logarithms.
- If M > 0, N > 0, a > 0 and a ≠ 1, then,
- Power Property of Logarithms
- If M > 0, a > 0, a ≠ 1 and p is any real number then,
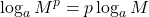
The log of a number raised to a power is the product of the power times the log of the number.
- If M > 0, a > 0, a ≠ 1 and p is any real number then,
- Properties of Logarithms Summary
If M > 0, N > 0, a > 0, a ≠ 1 and p is any real number then,
Property Base a Base e 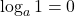
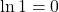
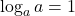
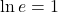
Inverse Properties 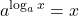
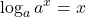
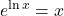
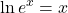
Product Property of Logarithms 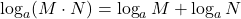
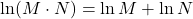
Quotient Property of Logarithms 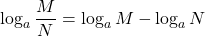
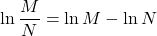
Power Property of Logarithms 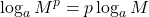
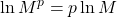
- Change-of-Base Formula
For any logarithmic bases a, b and M > 0,xxx xxx Formula 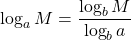
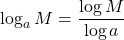
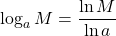
Base new base b new base 10 new base e
- Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction ↵
a rule of logarithms that states that the log of a product is equal to a sum of logarithms
a rule of logarithms that states that the log of a quotient is equal to a difference of logarithms
a rule of logarithms that states that the log of a power is equal to the product of the exponent and the log of its base
a formula for converting a logarithm with any base to a quotient of logarithms with any other base.

