Learning Module 06B Polynomial Functions
Zeros of Polynomial Functions
Learning Objectives
In this section, you will:
- Evaluate a polynomial using the Remainder Theorem.
- Use the Factor Theorem to solve a polynomial equation.
- Use the Rational Zero Theorem to find rational zeros.
- Find zeros of a polynomial function.
- Solve real-world applications of polynomial equations
A new bakery offers decorated sheet cakes for children’s birthday parties and other special occasions. The bakery wants the volume of a small cake to be 351 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be four inches longer than the width of the cake and the height of the cake to be one-third of the width. What should the dimensions of the cake pan be?
This problem can be solved by writing a cubic function and solving a cubic equation for the volume of the cake. In this section, we will discuss a variety of tools for writing polynomial functions and solving polynomial equations.
Evaluating a Polynomial Using the Remainder Theorem
In the last section, we learned how to divide polynomials. We can now use polynomial division to evaluate polynomials using the Remainder Theorem. If the polynomial is divided by ![]() the remainder may be found quickly by evaluating the polynomial function at
the remainder may be found quickly by evaluating the polynomial function at ![]() that is,
that is, ![]() Let’s walk through the proof of the theorem.
Let’s walk through the proof of the theorem.
Recall that the Division Algorithm states that, given a polynomial dividend ![]() and a non-zero polynomial divisor
and a non-zero polynomial divisor ![]() where the degree of
where the degree of ![]() is less than or equal to the degree of
is less than or equal to the degree of ![]() , there exist unique polynomials
, there exist unique polynomials ![]() and
and ![]() such that
such that
If the divisor, ![]() is
is ![]() this takes the form
this takes the form
Since the divisor ![]() is linear, the remainder will be a constant,
is linear, the remainder will be a constant, ![]() And, if we evaluate this for
And, if we evaluate this for ![]() we have
we have
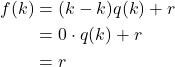
In other words, ![]() is the remainder obtained by dividing
is the remainder obtained by dividing ![]() by
by ![]()
The Remainder Theorem
If a polynomial ![]() is divided by
is divided by ![]() then the remainder is the value
then the remainder is the value ![]()
How To
Given a polynomial function ![]() evaluate
evaluate ![]() at
at ![]() using the Remainder Theorem.
using the Remainder Theorem.
- Use synthetic division to divide the polynomial by

- The remainder is the value
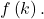
Using the Remainder Theorem to Evaluate a Polynomial
Use the Remainder Theorem to evaluate ![]() at
at ![]()
Show Solution
To find the remainder using the Remainder Theorem, use synthetic division to divide the polynomial by ![]()

The remainder is 25. Therefore, ![]()
Analysis
We can check our answer by evaluating ![]()
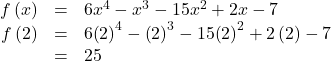
Try It
Use the Remainder Theorem to evaluate ![]() at
at ![]()
Show Solution
![]()
Using the Factor Theorem to Solve a Polynomial Equation
The Factor Theorem is another theorem that helps us analyze polynomial equations. It tells us how the zeros of a polynomial are related to the factors. Recall that the Division Algorithm.
If ![]() is a zero, then the remainder
is a zero, then the remainder ![]() is
is ![]() and
and ![]() or
or ![]()
Notice, written in this form, ![]() is a factor of
is a factor of ![]() We can conclude if
We can conclude if ![]() is a zero of
is a zero of ![]() then
then ![]() is a factor of
is a factor of ![]()
Similarly, if ![]() is a factor of
is a factor of ![]()
then the remainder of the Division Algorithm ![]() is 0. This tells us that
is 0. This tells us that ![]()
is a zero.
This pair of implications is the Factor Theorem. As we will soon see, a polynomial of degree ![]() in the complex number system will have
in the complex number system will have ![]() zeros. We can use the Factor Theorem to completely factor a polynomial into the product of
zeros. We can use the Factor Theorem to completely factor a polynomial into the product of ![]() factors. Once the polynomial has been completely factored, we can easily determine the zeros of the polynomial.
factors. Once the polynomial has been completely factored, we can easily determine the zeros of the polynomial.
The Factor Theorem
According to the Factor Theorem, ![]() is a zero of
is a zero of ![]() if and only if
if and only if ![]() is a factor of
is a factor of ![]()
How To
Given a factor and a third-degree polynomial, use the Factor Theorem to factor the polynomial.
- Use synthetic division to divide the polynomial by
- Confirm that the remainder is 0.
- Write the polynomial as the product of
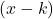 and the quadratic quotient.
and the quadratic quotient. - If possible, factor the quadratic.
- Write the polynomial as the product of factors.
Using the Factor Theorem to Find the Zeros of a Polynomial Expression
Show that ![]() is a factor of
is a factor of ![]() Find the remaining factors. Use the factors to determine the zeros of the polynomial.
Find the remaining factors. Use the factors to determine the zeros of the polynomial.
Show Solution
We can use synthetic division to show that ![]() is a factor of the polynomial.
is a factor of the polynomial.

The remainder is zero, so ![]() is a factor of the polynomial. We can use the Division Algorithm to write the polynomial as the product of the divisor and the quotient:
is a factor of the polynomial. We can use the Division Algorithm to write the polynomial as the product of the divisor and the quotient:
We can factor the quadratic factor to write the polynomial as
By the Factor Theorem, the zeros of ![]() are –2, 3, and 5.
are –2, 3, and 5.
Try It
Use the Factor Theorem to find the zeros of ![]() given that
given that ![]() is a factor of the polynomial.
is a factor of the polynomial.
Show Solution
The zeros are 2, –2, and –4.
Using the Rational Zero Theorem to Find Rational Zeros
Another use for the Remainder Theorem is to test whether a rational number is a zero for a given polynomial. But first we need a pool of rational numbers to test. The Rational Zero Theorem helps us to narrow down the number of possible rational zeros using the ratio of the factors of the constant term and factors of the leading coefficient of the polynomial
Consider a quadratic function with two zeros, ![]() and
and ![]() By the Factor Theorem, these zeros have factors associated with them. Let us set each factor equal to 0, and then construct the original quadratic function absent its stretching factor.
By the Factor Theorem, these zeros have factors associated with them. Let us set each factor equal to 0, and then construct the original quadratic function absent its stretching factor.

Notice that two of the factors of the constant term, 6, are the two numerators from the original rational roots: 2 and 3. Similarly, two of the factors from the leading coefficient, 20, are the two denominators from the original rational roots: 5 and 4.
We can infer that the numerators of the rational roots will always be factors of the constant term and the denominators will be factors of the leading coefficient. This is the essence of the Rational Zero Theorem; it is a means to give us a pool of possible rational zeros.
The Rational Zero Theorem
The Rational Zero Theorem states that, if the polynomial ![]() has integer coefficients, then every rational zero of
has integer coefficients, then every rational zero of ![]() has the form
has the form ![]() where
where ![]() is a factor of the constant term
is a factor of the constant term ![]() and
and ![]() is a factor of the leading coefficient
is a factor of the leading coefficient ![]()
When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.
How To
Given a polynomial function ![]() use the Rational Zero Theorem to find rational zeros.
use the Rational Zero Theorem to find rational zeros.
- Determine all factors of the constant term and all factors of the leading coefficient.
- Determine all possible values of
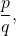 where
where 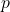 is a factor of the constant term and
is a factor of the constant term and 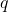 is a factor of the leading coefficient. Be sure to include both positive and negative candidates.
is a factor of the leading coefficient. Be sure to include both positive and negative candidates. - Determine which possible zeros are actual zeros by evaluating each case of
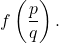
Listing All Possible Rational Zeros
List all possible rational zeros of ![]()
Show Solution
The only possible rational zeros of ![]() are the quotients of the factors of the last term, –4, and the factors of the leading coefficient, 2.
are the quotients of the factors of the last term, –4, and the factors of the leading coefficient, 2.
The constant term is –4; the factors of –4 are ![]()
The leading coefficient is 2; the factors of 2 are ![]()
If any of the four real zeros are rational zeros, then they will be of one of the following factors of –4 divided by one of the factors of 2.
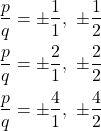
Note that ![]() and
and ![]() which have already been listed. So we can shorten our list.
which have already been listed. So we can shorten our list.
Using the Rational Zero Theorem to Find Rational Zeros
Use the Rational Zero Theorem to find the rational zeros of ![]()
Show Solution
The Rational Zero Theorem tells us that if ![]() is a zero of
is a zero of ![]() then
then ![]() is a factor of 1 and
is a factor of 1 and ![]() is a factor of 2.
is a factor of 2.

The factors of 1 are ![]() and the factors of 2 are
and the factors of 2 are ![]() and
and ![]() The possible values for
The possible values for ![]() are
are ![]() and
and ![]() These are the possible rational zeros for the function. We can determine which of the possible zeros are actual zeros by substituting these values for
These are the possible rational zeros for the function. We can determine which of the possible zeros are actual zeros by substituting these values for ![]() in
in ![]()
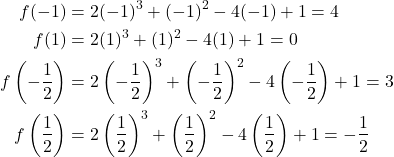
Of those, ![]() are not zeros of
are not zeros of ![]() 1 is the only rational zero of
1 is the only rational zero of ![]()
Try It
Use the Rational Zero Theorem to find the rational zeros of ![]()
Show Solution
There are no rational zeros.
Finding the Zeros of Polynomial Functions
The Rational Zero Theorem helps us to narrow down the list of possible rational zeros for a polynomial function. Once we have done this, we can use synthetic division repeatedly to determine all of the zeros of a polynomial function.
How To
Given a polynomial function ![]() use synthetic division to find its zeros.
use synthetic division to find its zeros.
- Use the Rational Zero Theorem to list all possible rational zeros of the function.
- Use synthetic division to evaluate a given possible zero by synthetically dividing the candidate into the polynomial. If the remainder is 0, the candidate is a zero. If the remainder is not zero, discard the candidate.
- Repeat step two using the quotient found with synthetic division. If possible, continue until the quotient is a quadratic.
- Find the zeros of the quadratic function. Two possible methods for solving quadratics are factoring and using the quadratic formula.
Finding the Zeros of a Polynomial Function with Repeated Real Zeros
Find the zeros of ![]()
Show Solution
The Rational Zero Theorem tells us that if ![]() is a zero of
is a zero of ![]() then
then ![]()
is a factor of –1 and ![]() is a factor of 4.
is a factor of 4.

The factors of ![]() are
are ![]() and the factors of
and the factors of ![]() are
are ![]() and
and ![]() The possible values for
The possible values for ![]() are
are ![]() and
and ![]() These are the possible rational zeros for the function. We will use synthetic division to evaluate each possible zero until we find one that gives a remainder of 0. Let’s begin with 1.
These are the possible rational zeros for the function. We will use synthetic division to evaluate each possible zero until we find one that gives a remainder of 0. Let’s begin with 1.

Dividing by ![]() gives a remainder of 0, so 1 is a zero of the function. The polynomial can be written as
gives a remainder of 0, so 1 is a zero of the function. The polynomial can be written as
The quadratic is a perfect square. ![]() can be written as
can be written as
We already know that 1 is a zero. The other zero will have a multiplicity of 2 because the factor is squared. To find the other zero, we can set the factor equal to 0.
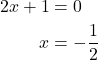
The zeros of the function are 1 and ![]() with multiplicity 2.
with multiplicity 2.
Using the Fundamental Theorem of Algebra
Now that we can find rational zeros for a polynomial function, we will look at a theorem that discusses the number of complex zeros of a polynomial function. The Fundamental Theorem of Algebra tells us that every polynomial function has at least one complex zero. This theorem forms the foundation for solving polynomial equations.
Suppose ![]() is a polynomial function of degree four, and
is a polynomial function of degree four, and ![]() The Fundamental Theorem of Algebra states that there is at least one complex solution, call it
The Fundamental Theorem of Algebra states that there is at least one complex solution, call it ![]() By the Factor Theorem, we can write
By the Factor Theorem, we can write ![]() as a product of
as a product of ![]() and a polynomial quotient. Since
and a polynomial quotient. Since ![]() is linear, the polynomial quotient will be of degree three. Now we apply the Fundamental Theorem of Algebra to the third-degree polynomial quotient. It will have at least one complex zero, call it
is linear, the polynomial quotient will be of degree three. Now we apply the Fundamental Theorem of Algebra to the third-degree polynomial quotient. It will have at least one complex zero, call it ![]() So we can write the polynomial quotient as a product of
So we can write the polynomial quotient as a product of ![]() and a new polynomial quotient of degree two. Continue to apply the Fundamental Theorem of Algebra until all of the zeros are found. There will be four of them and each one will yield a factor of
and a new polynomial quotient of degree two. Continue to apply the Fundamental Theorem of Algebra until all of the zeros are found. There will be four of them and each one will yield a factor of ![]()
The Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra states that, if ![]() is a polynomial of degree n > 0, then
is a polynomial of degree n > 0, then ![]() has at least one complex zero.
has at least one complex zero.
We can use this theorem to argue that, if ![]() is a polynomial of degree
is a polynomial of degree ![]() and
and ![]() is a non-zero real number, then
is a non-zero real number, then ![]() has exactly
has exactly ![]() linear factors
linear factors
where ![]() are complex numbers. Therefore,
are complex numbers. Therefore, ![]() has
has ![]() roots if we allow for multiplicities.
roots if we allow for multiplicities.
Does every polynomial have at least one imaginary zero?
No. Real numbers are a subset of complex numbers, but not the other way around. A complex number is not necessarily imaginary. Real numbers are also complex numbers.
Finding the Zeros of a Polynomial Function with Complex Zeros
Find the zeros of ![]()
Show Solution
The Rational Zero Theorem tells us that if ![]() is a zero of
is a zero of ![]() then
then ![]() is a factor of 3 and
is a factor of 3 and ![]() is a factor of 3.
is a factor of 3.

The factors of 3 are ![]() and
and ![]() The possible values for
The possible values for ![]() and therefore the possible rational zeros for the function, are
and therefore the possible rational zeros for the function, are ![]() We will use synthetic division to evaluate each possible zero until we find one that gives a remainder of 0. Let’s begin with –3.
We will use synthetic division to evaluate each possible zero until we find one that gives a remainder of 0. Let’s begin with –3.

Dividing by ![]() gives a remainder of 0, so –3 is a zero of the function. The polynomial can be written as
gives a remainder of 0, so –3 is a zero of the function. The polynomial can be written as
We can then set the quadratic equal to 0 and solve to find the other zeros of the function.
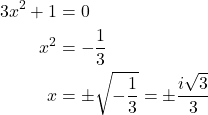
The zeros of ![]() are –3 and
are –3 and ![]()
Analysis
Look at the graph of the function ![]() . Notice that, at
. Notice that, at ![]() the graph crosses the x-axis, indicating an odd multiplicity (1) for the zero
the graph crosses the x-axis, indicating an odd multiplicity (1) for the zero ![]() Also note the presence of the two turning points. This means that, since there is a 3rd degree polynomial, we are looking at the maximum number of turning points. So, the end behavior of increasing without bound to the right and decreasing without bound to the left will continue. Thus, all the x-intercepts for the function are shown. So either the multiplicity of
Also note the presence of the two turning points. This means that, since there is a 3rd degree polynomial, we are looking at the maximum number of turning points. So, the end behavior of increasing without bound to the right and decreasing without bound to the left will continue. Thus, all the x-intercepts for the function are shown. So either the multiplicity of ![]() is 1 and there are two complex solutions, which is what we found, or the multiplicity at
is 1 and there are two complex solutions, which is what we found, or the multiplicity at ![]() is three. Either way, our result is correct.
is three. Either way, our result is correct.

Try It
Find the zeros of ![]()
Show Solution
The zeros are ![]() , and
, and ![]() .
.
Using the Linear Factorization Theorem to Find Polynomials with Given Zeros
A vital implication of the Fundamental Theorem of Algebra, as we stated above, is that a polynomial function of degree ![]()
will have ![]() zeros in the set of complex numbers, if we allow for multiplicities. This means that we can factor the polynomial function into
zeros in the set of complex numbers, if we allow for multiplicities. This means that we can factor the polynomial function into ![]() factors. The Linear Factorization Theorem tells us that a polynomial function will have the same number of factors as its degree, and that each factor will be in the form
factors. The Linear Factorization Theorem tells us that a polynomial function will have the same number of factors as its degree, and that each factor will be in the form ![]() where
where ![]() is a complex number.
is a complex number.
Let ![]() be a polynomial function with real coefficients, and suppose
be a polynomial function with real coefficients, and suppose ![]() is a zero of
is a zero of ![]() Then, by the Factor Theorem,
Then, by the Factor Theorem, ![]() is a factor of
is a factor of ![]() For
For ![]() to have real coefficients,
to have real coefficients, ![]() must also be a factor of
must also be a factor of ![]() This is true because any factor other than
This is true because any factor other than ![]() when multiplied by
when multiplied by ![]() will leave imaginary components in the product. Only multiplication with conjugate pairs will eliminate the imaginary parts and result in real coefficients. In other words, if a polynomial function
will leave imaginary components in the product. Only multiplication with conjugate pairs will eliminate the imaginary parts and result in real coefficients. In other words, if a polynomial function ![]() with real coefficients has a complex zero
with real coefficients has a complex zero ![]()
then the complex conjugate ![]() must also be a zero of
must also be a zero of ![]() This is called the Complex Conjugate Theorem.
This is called the Complex Conjugate Theorem.
Complex Conjugate Theorem
According to the Linear Factorization Theorem, a polynomial function will have the same number of factors as its degree, and each factor will be in the form ![]() , where
, where ![]() is a complex number.
is a complex number.
If the polynomial function ![]() has real coefficients and a complex zero in the form
has real coefficients and a complex zero in the form ![]() then the complex conjugate of the zero,
then the complex conjugate of the zero, ![]() is also a zero.
is also a zero.
How To
Given the zeros of a polynomial function ![]() and a point (c, f(c)) on the graph of
and a point (c, f(c)) on the graph of ![]() use the Linear Factorization Theorem to find the polynomial function.
use the Linear Factorization Theorem to find the polynomial function.
- Use the zeros to construct the linear factors of the polynomial.
- Multiply the linear factors to expand the polynomial.
- Substitute
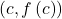 into the function to determine the leading coefficient.
into the function to determine the leading coefficient. - Simplify.
Using the Linear Factorization Theorem to Find a Polynomial with Given Zeros
Find a fourth degree polynomial with real coefficients that has zeros of –3, 2, ![]() such that
such that ![]()
Show Solution
Because ![]() is a zero, by the Complex Conjugate Theorem
is a zero, by the Complex Conjugate Theorem ![]() is also a zero. The polynomial must have factors of
is also a zero. The polynomial must have factors of ![]() and
and ![]() Since we are looking for a degree 4 polynomial, and now have four zeros, we have all four factors. Let’s begin by multiplying these factors.
Since we are looking for a degree 4 polynomial, and now have four zeros, we have all four factors. Let’s begin by multiplying these factors.
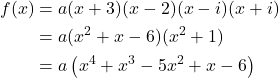
We need to find a to ensure ![]() Substitute
Substitute ![]() and
and ![]() into
into ![]()
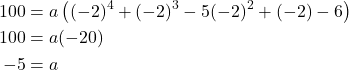
So the polynomial function is
or
Analysis
We found that both ![]() and
and ![]() were zeros, but only one of these zeros needed to be given. If
were zeros, but only one of these zeros needed to be given. If ![]() is a zero of a polynomial with real coefficients, then
is a zero of a polynomial with real coefficients, then ![]() must also be a zero of the polynomial because
must also be a zero of the polynomial because ![]() is the complex conjugate of
is the complex conjugate of ![]()
If ![]() were given as a zero of a polynomial with real coefficients, would
were given as a zero of a polynomial with real coefficients, would ![]() also need to be a zero?
also need to be a zero?
Yes. When any complex number with an imaginary component is given as a zero of a polynomial with real coefficients, the conjugate must also be a zero of the polynomial.
Try It
Find a third degree polynomial with real coefficients that has zeros of 5 and ![]() such that
such that ![]()
Show Solution
![]()
Using Descartes’ Rule of Signs
There is a straightforward way to determine the possible numbers of positive and negative real zeros for any polynomial function. If the polynomial is written in descending order, Descartes’ Rule of Signs tells us of a relationship between the number of sign changes in ![]() and the number of positive real zeros. For example, the polynomial function below has one sign change. The function,
and the number of positive real zeros. For example, the polynomial function below has one sign change. The function, ![]() , has one sign change between
, has one sign change between ![]() and
and ![]() . This tells us that the function must have 1 positive real zero.
. This tells us that the function must have 1 positive real zero.
There is a similar relationship between the number of sign changes in ![]() and the number of negative real zeros. The function,
and the number of negative real zeros. The function, ![]() , has three sign changes between
, has three sign changes between ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . In this case,
. In this case, ![]() has 3 sign changes. This tells us that
has 3 sign changes. This tells us that ![]() could have 3 or 1 negative real zeros.
could have 3 or 1 negative real zeros.
Descartes’ Rule of Signs
According to Descartes’ Rule of Signs, if we let ![]() be a polynomial function with real coefficients:
be a polynomial function with real coefficients:
- The number of positive real zeros is either equal to the number of sign changes of
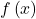 or is less than the number of sign changes by an even integer.
or is less than the number of sign changes by an even integer. - The number of negative real zeros is either equal to the number of sign changes of
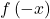 or is less than the number of sign changes by an even integer.
or is less than the number of sign changes by an even integer.
Using Descartes’ Rule of Signs
Use Descartes’ Rule of Signs to determine the possible numbers of positive and negative real zeros for ![]()
Show Solution
Begin by determining the number of sign changes. ![]() has two sign changes. One between
has two sign changes. One between ![]() and
and ![]() and one between
and one between ![]() and
and ![]() . There are two sign changes, so there are either 2 or 0 positive real roots.
. There are two sign changes, so there are either 2 or 0 positive real roots.
Next, we examine ![]() to determine the number of negative real roots.
to determine the number of negative real roots. ![]() has two sign changes. One between
has two sign changes. One between ![]() and
and ![]() and one between
and one between ![]() and
and ![]() . Again, there are two sign changes, so there are either 2 or 0 negative real roots.
. Again, there are two sign changes, so there are either 2 or 0 negative real roots.
There are four possibilities, as we can see in the table below.
| Positive Real Zeros |
Negative Real Zeros |
Complex Zeros |
Total Zeros |
|---|---|---|---|
| 2 | 2 | 0 | 4 |
| 2 | 0 | 2 | 4 |
| 0 | 2 | 2 | 4 |
| 0 | 0 | 4 | 4 |
We can confirm the numbers of positive and negative real roots by examining a graph of the function. We can see from the graph that the function has 0 positive real roots and 2 negative real roots.
Try It
Use Descartes’ Rule of Signs to determine the maximum possible numbers of positive and negative real zeros for ![]() Use a graph to verify the numbers of positive and negative real zeros for the function.
Use a graph to verify the numbers of positive and negative real zeros for the function.
Show Solution
There must be 4, 2, or 0 positive real roots and 0 negative real roots. The graph shows that there are 2 positive real zeros and 0 negative real zeros.
Access these online resources for additional instruction and practice with zeros of polynomial functions.
Key Concepts
- To find
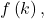 determine the remainder of the polynomial
determine the remainder of the polynomial 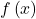 when it is divided by
when it is divided by  This is known as the Remainder Theorem.
This is known as the Remainder Theorem. - According to the Factor Theorem,
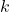 is a zero of
is a zero of 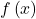 if and only if
if and only if 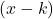 is a factor of
is a factor of 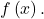
- According to the Rational Zero Theorem, each rational zero of a polynomial function with integer coefficients will be equal to a factor of the constant term divided by a factor of the leading coefficient.
- When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.
- Synthetic division can be used to find the zeros of a polynomial function.
- According to the Fundamental Theorem, every polynomial function has at least one complex zero.
- Every polynomial function with degree greater than 0 has at least one complex zero.
- Allowing for multiplicities, a polynomial function will have the same number of factors as its degree. Each factor will be in the form
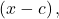 where
where  is a complex number.
is a complex number. - The number of positive real zeros of a polynomial function is either the number of sign changes of the function or less than the number of sign changes by an even integer.
- The number of negative real zeros of a polynomial function is either the number of sign changes of
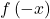 or less than the number of sign changes by an even integer.
or less than the number of sign changes by an even integer.

