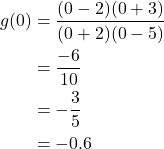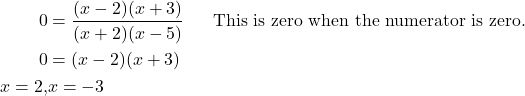Learning Module 07B Rational Functions & Graphs
Analyzing Rational Functions
Learning Objectives
In this section, you will:
- Use arrow notation.
- Solve applied problems involving rational functions.
- Find the domains of rational functions.
- Identify vertical asymptotes.
- Identify horizontal asymptotes.
- Identify
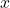 intercept(s) for rational functions.
intercept(s) for rational functions. - Identify
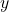 intercept for rational functions.
intercept for rational functions.
Suppose we know that the cost of making a product is dependent on the number of items ![]() produced. This is given by the equation
produced. This is given by the equation ![]() .If we want to know the average cost for producing
.If we want to know the average cost for producing ![]() items, we would divide the cost function by the number of items
items, we would divide the cost function by the number of items ![]() .
.
The average cost function, which yields the average cost per item for ![]() items produced, is
items produced, is
Many other application problems require finding an average value in a similar way, giving us variables in the denominator. Written without a variable in the denominator, this function will contain a negative integer power.
In the last few sections, we have worked with polynomial functions, which are functions with non-negative integers for exponents. In this section, we explore rational functions, which have variables in the denominator.
Using Arrow Notation
We have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Examine these toolkit function graphs and notice some of their features.
Several things are apparent if we examine the graph of ![]() .
.
- On the left branch of the graph, the curve approaches the x-axis
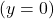 as
as 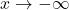 .
. - As the graph approaches
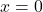 from the left, the curve drops, but as we approach zero from the right, the curve rises.
from the left, the curve drops, but as we approach zero from the right, the curve rises. - Finally, on the right branch of the graph, the curves approaches the x-axis
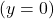 as
as 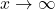 .
.
To summarize, we use arrow notation to show that ![]() or
or ![]() is approaching a particular value.
is approaching a particular value.
| Symbol | Meaning |
|---|---|
| the output approaches infinity (the output increases without bound) | |
| the output approaches negative infinity (the output decreases without bound) | |
| the output approaches |
Local Behavior of 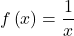
Let’s begin by looking at the reciprocal function ![]() .We cannot divide by zero, which means the function is undefined at
.We cannot divide by zero, which means the function is undefined at ![]() so zero is not in the domain. As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in the table below. This is a similar concept to vertical asymptotes for logarithmic functions. The difference for the reciprocal function,
so zero is not in the domain. As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in the table below. This is a similar concept to vertical asymptotes for logarithmic functions. The difference for the reciprocal function, ![]() , is that the graph behavior around the asymptotes is opposite. We use specific left and and right hand arrow notation to denote this change in behavior.
, is that the graph behavior around the asymptotes is opposite. We use specific left and and right hand arrow notation to denote this change in behavior.
| |
–0.1 | –0.01 | –0.001 | –0.0001 |
| |
–10 | –100 | –1000 | –10,000 |
We write in arrow notation as ![]() ,
, ![]() . Notice when the
. Notice when the ![]() values are approaching zero from the left, or values that are smaller than 0, we use the notation
values are approaching zero from the left, or values that are smaller than 0, we use the notation ![]() .
.
As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). We can see this behavior in the table below.
| |
0.1 | 0.01 | 0.001 | 0.0001 |
| |
10 | 100 | 1000 | 10,000 |
We write in arrow notation as ![]() . Notice when the
. Notice when the ![]() values are approaching zero from the right, or values that are larger than 0, we use the notation
values are approaching zero from the right, or values that are larger than 0, we use the notation ![]() .
.
This behavior creates a vertical asymptote, which is a vertical line that the graph approaches but never crosses. In this case, the graph is approaching the vertical line ![]() as the input becomes close to zero.
as the input becomes close to zero.
Vertical Asymptote
A vertical asymptote of a graph is a vertical line ![]() where the graph tends toward positive or negative infinity as the inputs approach
where the graph tends toward positive or negative infinity as the inputs approach ![]() .We write
.We write
End Behavior of 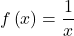
As the values of ![]() approach infinity, the function values approach 0. As the values of
approach infinity, the function values approach 0. As the values of ![]() approach negative infinity, the function values approach 0. Symbolically, using arrow notation.
approach negative infinity, the function values approach 0. Symbolically, using arrow notation.
As ![]()
![]() and as
and as ![]()
![]() .
.
Based on this overall behavior and the graph, we can see that the function approaches 0 but never actually reaches 0; it seems to level off as the inputs become large. This behavior creates a horizontal asymptote, a horizontal line that the graph approaches as the input increases or decreases without bound. In this case, the graph is approaching the horizontal line ![]() This is a similar concept to horizontal asymptotes for exponential functions.
This is a similar concept to horizontal asymptotes for exponential functions.
Horizontal Asymptote
A horizontal asymptote of a graph is a horizontal line ![]() where the graph approaches the line as the inputs increase or decrease without bound. We write
where the graph approaches the line as the inputs increase or decrease without bound. We write
Using Arrow Notation
Use arrow notation to describe the end behavior and local behavior of the function graphed below.
Show Solution
Notice that the graph is showing a vertical asymptote at ![]() which tells us that the function is undefined at
which tells us that the function is undefined at ![]() .
.
And as the inputs decrease without bound, the graph appears to be leveling off at output values of 4, indicating a horizontal asymptote at ![]() .As the inputs increase without bound, the graph levels off at 4.
.As the inputs increase without bound, the graph levels off at 4.
Try It
Use arrow notation to describe the end behavior and local behavior for the reciprocal squared function.
Show Solution
End behavior: as ![]() Local behavior: as
Local behavior: as ![]() (there are no x– or y-intercepts)
(there are no x– or y-intercepts)
Solving Applied Problems Involving Rational Functions
A rational function is a function that can be written as the quotient of two polynomial functions. Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.
Rational Function
A rational function is a function that can be written as the quotient of two polynomial functions ![]() and
and ![]() .
.
Solving an Applied Problem Involving a Rational Function
A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the ratio of sugar to water, in pounds per gallon in the tank after 12 minutes. Is that a greater ratio of sugar to water, in pounds per gallon than at the beginning?
Show Solution
Let ![]() be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:
be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:
![]()
The ratio of sugar to water, in pounds per gallon ![]() will be the ratio of pounds of sugar to gallons of water
will be the ratio of pounds of sugar to gallons of water
![]()
The ratio of sugar to water, in pounds per gallon after 12 minutes is given by evaluating ![]() at
at ![]() .
.
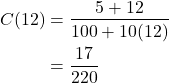
This means the ratio of sugar to water, in pounds per gallon is 17 pounds of sugar to 220 gallons of water.
At the beginning, the ratio of sugar to water, in pounds per gallon is
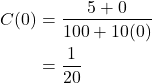
Since ![]() the ratio of sugar to water, in pounds per gallon is greater after 12 minutes than at the beginning.
the ratio of sugar to water, in pounds per gallon is greater after 12 minutes than at the beginning.
Finding the Domains of Rational Functions
A vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A reciprocal function cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.
Domain of a Rational Function
The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.
How To
Given a rational function, find the domain.
- Set the denominator equal to zero.
- Solve to find the x-values that cause the denominator to equal zero.
- The domain is all real numbers except those found in Step 2.
Finding the Domain of a Rational Function
Find the domain of ![]() .
.
Show Solution
Begin by setting the denominator equal to zero and solving.
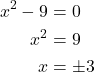
The denominator is equal to zero when ![]() .The domain of the function is all real numbers except
.The domain of the function is all real numbers except ![]() .
.
Try It
Find the domain of ![]() .
.
Show Solution
The domain is all real numbers except ![]() and
and ![]() .
.
Identifying Vertical Asymptotes of Rational Functions
By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location.
Vertical Asymptotes
The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.
Given a rational function, identify any vertical asymptotes of its graph.
- Factor the numerator and denominator.
- Note any restrictions in the domain of the function.
- Reduce the expression by canceling common factors in the numerator and the denominator.
- Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
- Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities, or “holes.”
Identifying Vertical Asymptotes
Find the vertical asymptotes of the graph of ![]() .
.
Show Solution
First, factor the numerator and denominator.
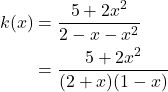
To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:
![]()
Neither ![]() nor
nor ![]() are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph confirms the location of the two vertical asymptotes.
are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph confirms the location of the two vertical asymptotes.
Removable Discontinuities
Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity.
For example, the function ![]() may be re-written by factoring the numerator and the denominator.
may be re-written by factoring the numerator and the denominator.
![]()
Removable Discontinuities of Rational Functions
A removable discontinuity occurs in the graph of a rational function at ![]() if
if ![]() is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.
is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.
Identifying Vertical Asymptotes and Removable Discontinuities for a Graph
Find the vertical asymptotes and removable discontinuities of the graph ![]()
Show Solution
Factor the numerator and the denominator.
![]() .
.
Notice that there is a common factor in the numerator and the denominator, ![]() . The zero for this factor is
. The zero for this factor is ![]() . This is the location of the removable discontinuity.
. This is the location of the removable discontinuity.
Notice that there is a factor in the denominator that is not in the numerator, ![]() . The zeros for this factor is
. The zeros for this factor is ![]() . The vertical asymptote is
. The vertical asymptote is ![]() .
.
Identifying Horizontal Asymptotes of Rational Functions
While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the function that is the ratio of the leading terms.
There are three distinct outcomes when checking for horizontal asymptotes:
Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at ![]() .
.
In this case, the end behavior is ![]() .This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function
.This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function ![]() and the outputs will approach zero, resulting in a horizontal asymptote at
and the outputs will approach zero, resulting in a horizontal asymptote at ![]() . Note that this graph crosses the horizontal asymptote. We can cross horizontal asymptotes when it is necessary to create a continuous graph connecting the
. Note that this graph crosses the horizontal asymptote. We can cross horizontal asymptotes when it is necessary to create a continuous graph connecting the ![]() intercept on one side of the horizontal asymptote to a
intercept on one side of the horizontal asymptote to a ![]() on the other side.
on the other side.
Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.
In this case, the end behavior is ![]() .This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function
.This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function ![]() .As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of
.As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of ![]() looks like a diagonal line, and since
looks like a diagonal line, and since ![]() will behave similarly to
will behave similarly to ![]() it will approach a line close to
it will approach a line close to ![]() . This line is a slant asymptote.
. This line is a slant asymptote.
To find the equation of the slant asymptote, divide ![]() .The quotient is
.The quotient is ![]() and the remainder is 2. The slant asymptote is the graph of the line
and the remainder is 2. The slant asymptote is the graph of the line ![]() .
.
Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at ![]() where
where ![]() and
and ![]() are the leading coefficients of
are the leading coefficients of ![]() and
and ![]() for
for ![]() .
.
In this case, the end behavior is ![]() .This tells us that as the inputs grow large, this function will behave like the function
.This tells us that as the inputs grow large, this function will behave like the function ![]() which is a horizontal line. As
which is a horizontal line. As ![]() resulting in a horizontal asymptote at
resulting in a horizontal asymptote at ![]() . Note that this graph crosses the horizontal asymptote.
. Note that this graph crosses the horizontal asymptote.
Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.
It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function
with end behavior
the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.
Horizontal Asymptotes of Rational Functions
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
- Degree of numerator is less than degree of denominator: horizontal asymptote at
 .
. - Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
- Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.
Identifying Horizontal and Slant Asymptotes
For the functions listed, identify the horizontal or slant asymptote.
Show Solution
For these solutions, we will use ![]() .
.
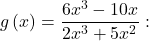 The degree of
The degree of 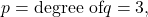 so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at
so we can find the horizontal asymptote by taking the ratio of the leading terms. There is a horizontal asymptote at 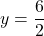 or
or 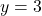 .
.

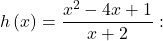 The degree of
The degree of 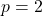 and degree of
and degree of 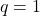 .Since
.Since 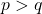 by 1, there is a slant asymptote found at
by 1, there is a slant asymptote found at 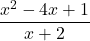 .
. The quotient is
The quotient is 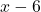 and the remainder is 13. There is a slant asymptote at
and the remainder is 13. There is a slant asymptote at 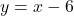 .
.

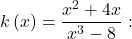 The degree of
The degree of 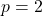 degree of
degree of 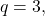 so there is a horizontal asymptote
so there is a horizontal asymptote 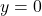 .
.
Identifying Horizontal Asymptotes
In the sugar concentration problem earlier, we created the equation ![]() .
.
Find the horizontal asymptote and interpret it in context of the problem.
Show Solution
Both the numerator and denominator are linear (degree 1). Because the degrees are equal, there will be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is ![]() with coefficient 1. In the denominator, the leading term is
with coefficient 1. In the denominator, the leading term is ![]() with coefficient 10. The horizontal asymptote will be at the ratio of these values:
with coefficient 10. The horizontal asymptote will be at the ratio of these values:
This function will have a horizontal asymptote at ![]() .
.
This tells us that as the values of t increase, the values of ![]() will approach
will approach ![]() .In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or
.In context, this means that, as more time goes by, the concentration of sugar in the tank will approach one-tenth of a pound of sugar per gallon of water or ![]() pounds per gallon.
pounds per gallon.
Intercepts of Rational Functions
A rational function will have a y-intercept at ![]() if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero.
if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero.
Likewise, a rational function will have x-intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x-intercepts can only occur when the numerator of the rational function is equal to zero.
Finding the Intercepts of a Rational Function
Find the intercepts of ![]()
Try It
Given the reciprocal squared function that is shifted right 3 units and down 4 units, write this as a rational function. Then, find the x– and y-intercepts and the horizontal and vertical asymptotes.
Show Solution
For the transformed reciprocal squared function, we find the rational form 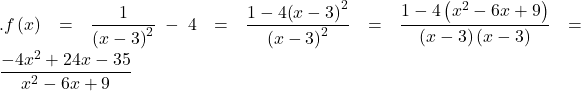
Because the numerator is the same degree as the denominator we know that as ![]() so
so ![]() is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is
is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is ![]() because as
because as ![]() ,
, ![]() .We then set the numerator equal to 0 and find the x-intercepts are at
.We then set the numerator equal to 0 and find the x-intercepts are at ![]() and
and ![]() .Finally, we evaluate the function at 0 and find the y-intercept to be at
.Finally, we evaluate the function at 0 and find the y-intercept to be at ![]() .
.
Key Concepts
- We can use arrow notation to describe local behavior and end behavior of the toolkit functions
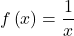 and
and 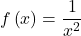 .
. - A function that levels off at a horizontal value has a horizontal asymptote. A function can have more than one vertical asymptote.
- Application problems involving rates and concentrations often involve rational functions.
- The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.
- The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero.
- A removable discontinuity might occur in the graph of a rational function if an input causes both numerator and denominator to be zero.
- A rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
- Graph rational functions by finding the intercepts, behavior at the intercepts and asymptotes, and end behavior.
- If a rational function has x-intercepts at
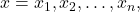 vertical asymptotes at
vertical asymptotes at 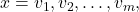 and no
and no 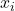 = any
= any 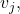 then the function can be written in the form
then the function can be written in the form
![]()