Learning Module 05B Quadratic Equations & Quadratic Functions
Quadratic Equations
Learning Objectives
In this section you will:
- Solve quadratic equations by factoring.
- Solve quadratic equations by the square root property.
- Solve quadratic equations by using the quadratic formula.
- Define and classify solutions of a quadratic equation using the discriminant.

The computer monitor on the left is a 23.6-inch model and the one on the right is a 27-inch model. Proportionally, the monitors appear very similar. If there is a limited amount of space and we desire the largest monitor possible, how do we decide which one to choose? In this section, we will learn how to solve problems such as this using four different methods.
Solving Quadratic Equations by Factoring
An equation containing a second-degree polynomial is called a quadratic equation. For example, equations such as ![]() and
and ![]() are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics.
are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics.
Often the easiest method of solving a quadratic equation is factoring. Factoring means finding expressions that can be multiplied together to give the expression on one side of the equation.
If a quadratic equation can be factored, it is written as a product of linear terms. Solving by factoring depends on the zero-product property, which states that if ![]() then
then ![]() or
or ![]() where a and b are real numbers or algebraic expressions. In other words, if the product of two numbers or two expressions equals zero, then one of the numbers or one of the expressions must equal zero because zero multiplied by anything equals zero.
where a and b are real numbers or algebraic expressions. In other words, if the product of two numbers or two expressions equals zero, then one of the numbers or one of the expressions must equal zero because zero multiplied by anything equals zero.
Multiplying the factors expands the equation to a string of terms separated by plus or minus signs. So, in that sense, the operation of multiplication undoes the operation of factoring. For example, expand the factored expression ![]() by multiplying the two factors together.
by multiplying the two factors together.
![]()
The product is a quadratic expression. Set equal to zero, ![]() is a quadratic equation. If we were to factor the equation, we would get back the factors we multiplied.
is a quadratic equation. If we were to factor the equation, we would get back the factors we multiplied.
The process of factoring a quadratic equation depends on the leading coefficient, whether it is 1 or another integer. We will look at both situations; but first, we want to confirm that the equation is written in standard form, ![]() where a, b, and c are real numbers, and
where a, b, and c are real numbers, and ![]() The equation
The equation ![]() is in standard form.
is in standard form.
We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF), and for equations that have special factoring formulas as well, such as the difference of squares, both of which we will see later in this section.
The Zero-Product Property and Quadratic Equations
The zero-product property states
where a and b are real numbers or algebraic expressions.
A quadratic equation is an equation containing a second-degree polynomial; for example
where a, b, and c are real numbers, and if ![]() it is in standard form.
it is in standard form.
Solving Quadratics with a Leading Coefficient of 1
In the quadratic equation ![]() the leading coefficient, or the coefficient of
the leading coefficient, or the coefficient of ![]() is 1. We have one method of factoring quadratic equations in this form.
is 1. We have one method of factoring quadratic equations in this form.
How To
Given a quadratic equation with the leading coefficient of 1, solve it.
- Find two numbers whose product equals c and whose sum equals b.
- Use those numbers to write two factors of the form
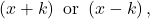 where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and
where k is one of the numbers found in step 1. Use the numbers exactly as they are. In other words, if the two numbers are 1 and 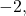 the factors are
the factors are 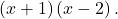
- Solve using the zero-product property by setting each factor equal to zero and solving for the variable.
Solving a Quadratic Equation by Factoring when the Leading Coefficient is not 1
Factor and solve the equation: ![]()
Show Solution
To factor ![]() we look for two numbers whose product equals
we look for two numbers whose product equals ![]() and whose sum equals 1. Begin by looking at the possible factors of
and whose sum equals 1. Begin by looking at the possible factors of ![]()
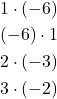
The last pair, ![]() sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.
sums to 1, so these are the numbers. Note that only one pair of numbers will work. Then, write the factors.
To solve this equation, we use the zero-product property. Set each factor equal to zero and solve.
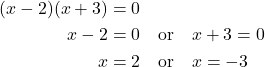
The two solutions are ![]() and
and ![]() We can see how the solutions relate to the graph. The solutions are the x-intercepts of
We can see how the solutions relate to the graph. The solutions are the x-intercepts of ![]()

Try It
Factor and solve the quadratic equation: ![]()
Show Solution
![]()
Solve the Quadratic Equation by Factoring
Solve the quadratic equation by factoring: ![]()
Show Solution
Find two numbers whose product equals ![]() and whose sum equals
and whose sum equals ![]() List the factors of
List the factors of ![]()
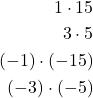
The numbers that add to 8 are 3 and 5. Then, write the factors, set each factor equal to zero, and solve.
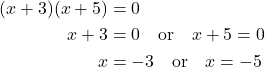
The solutions are ![]() and
and ![]()
Try It
Solve the quadratic equation by factoring: ![]()
Show Solution
![]()
![]()
![]()
Using the Zero-Product Property to Solve a Quadratic Equation Written as the Difference of Squares
Solve the difference of squares equation using the zero-product property: ![]()
Show Solution
Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property.
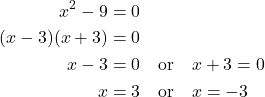
The solutions are ![]() and
and ![]()
Try It
Solve by factoring: ![]()
Show Solution
![]()
![]()
![]()
Solving a Quadratic Equation by Factoring when the Leading Coefficient is not 1
When the leading coefficient is not 1, we factor a quadratic equation using the method called grouping, which requires four terms. With the equation in standard form, let’s review the grouping procedures:
How To
- With the quadratic in standard form,
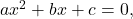 multiply
multiply 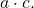
- Find two numbers whose product equals
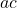 and whose sum equals
and whose sum equals 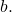
- Rewrite the equation replacing the
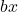 term with two terms using the numbers found in step 1 as coefficients of x.
term with two terms using the numbers found in step 1 as coefficients of x. - Factor the first two terms and then factor the last two terms. The expressions in parentheses must be exactly the same to use grouping.
- Factor out the expression in parentheses.
- Set the expressions equal to zero and solve for the variable.
Solving a Quadratic Equation Using Grouping
Use grouping to factor and solve the quadratic equation: ![]()
Show Solution
First, multiply ![]() Then list the factors of
Then list the factors of ![]()
![]()
The only pair of factors that sums to ![]() is
is ![]() Rewrite the equation replacing the b term,
Rewrite the equation replacing the b term, ![]() with two terms using 3 and 12 as coefficients of x. Factor the first two terms, and then factor the last two terms.
with two terms using 3 and 12 as coefficients of x. Factor the first two terms, and then factor the last two terms.
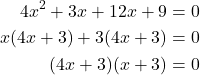
Solve using the zero-product property.
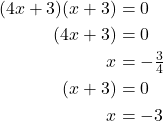

The solutions are ![]()
![]()
Try It
Solve using factoring by grouping: ![]()
Show Solution
![]()
![]()
![]()
Solving a Polynomial of Higher Degree by Factoring
Solve the equation by factoring: ![]()
Show Solution
This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out ![]() from all of the terms and then proceed with grouping.
from all of the terms and then proceed with grouping.
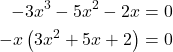
Use grouping on the expression in parentheses.
![Rendered by QuickLaTeX.com \begin{align*} -x\left(3x^{2} + 3x + 2x + 2\right) &= 0 \\ -x\left[3x(x+1) + 2(x+1)\right] &= 0 \\ -x(3x+2)(x+1) &= 0 \end{align*}](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9febbd86bff1a9d971e8b094db1e330a_l3.png)
Now, we use the zero-product property. Notice that we have three factors.
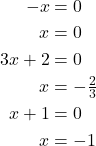
The solutions are ![]()
![]() and
and ![]()
Try It
Solve by factoring: ![]()
Show Solution
![]()
Using the Square Root Property
When there is no linear term in the equation, another method of solving a quadratic equation is by using the square root property, in which we isolate the ![]() term and take the square root of the number on the other side of the equals sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the
term and take the square root of the number on the other side of the equals sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the ![]() term so that the square root property can be used.
term so that the square root property can be used.
The Square Root Property
With the ![]() term isolated, the square root property states that:
term isolated, the square root property states that:
where k is a nonzero real number.
How To
Given a quadratic equation with an ![]() term but no
term but no ![]() term, use the square root property to solve it.
term, use the square root property to solve it.
- Isolate the
 term on one side of the equal sign.
term on one side of the equal sign. - Take the square root of both sides of the equation, putting a
 sign before the expression on the side opposite the squared term.
sign before the expression on the side opposite the squared term. - Simplify the numbers on the side with the
 sign.
sign.
Solving a Simple Quadratic Equation Using the Square Root Property
Solve the quadratic using the square root property: ![]()
Show Solution
Take the square root of both sides, and then simplify the radical. Remember to use a ![]() sign before the radical symbol.
sign before the radical symbol.
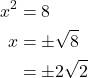
The solutions are ![]()
![]()
Solving a Quadratic Equation Using the Square Root Property
Solve the quadratic equation: ![]()
Show Solution
First, isolate the ![]() term. Then take the square root of both sides.
term. Then take the square root of both sides.
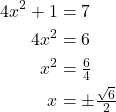
The solutions are ![]()
![]()
Try It
Solve the quadratic equation using the square root property: ![]()
Show Solution
![]()
Using the Quadratic Formula
The third method of solving a quadratic equation is by using the quadratic formula, a formula that will solve all quadratic equations. Although the quadratic formula works on any quadratic equation in standard form, it is easy to make errors in substituting the values into the formula. Pay close attention when substituting, and use parentheses when inserting a negative number.
We can derive the quadratic formula by completing the square. We will assume that the leading coefficient is positive; if it is negative, we can multiply the equation by ![]() and obtain a positive a. Given
and obtain a positive a. Given ![]()
![]() we will complete the square as follows:
we will complete the square as follows:
- First, move the constant term to the right side of the equal sign:
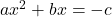
- As we want the leading coefficient to equal 1, divide through by a:
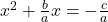
- Then, find
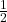 of the middle term, and add
of the middle term, and add 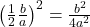 to both sides of the equal sign:
to both sides of the equal sign:
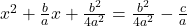
- Next, write the left side as a perfect square. Find the common denominator of the right side and write it as a single fraction:
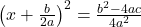
- Now, use the square root property, which gives
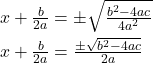
- Finally, add
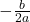 to both sides of the equation and combine the terms on the right side. Thus,
to both sides of the equation and combine the terms on the right side. Thus,
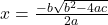
The Quadratic Formula
Written in standard form, ![]() any quadratic equation can be solved using the quadratic formula:
any quadratic equation can be solved using the quadratic formula:
where a, b, and c are real numbers and ![]()
How To
Given a quadratic equation, solve it using the quadratic formula
- Make sure the equation is in standard form:
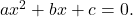
- Make note of the values of the coefficients and constant term,
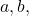 and
and 
- Carefully substitute the values noted in step 2 into the equation. To avoid needless errors, use parentheses around each number input into the formula.
- Calculate and solve.
Solve the Quadratic Equation Using the Quadratic Formula
Solve the quadratic equation: ![]()
Show Solution
Identify the coefficients: ![]() Then use the quadratic formula.
Then use the quadratic formula.
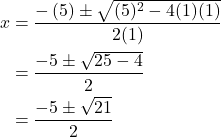
Solving a Quadratic Equation with the Quadratic Formula
Use the quadratic formula to solve ![]()
Show Solution
First, we identify the coefficients: ![]() and
and ![]()
Substitute these values into the quadratic formula.
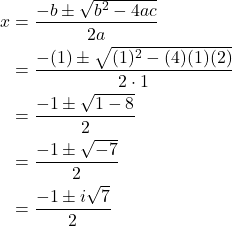
The solutions to the equation are ![]() and
and ![]() or
or ![]() and
and ![]()
Try It
Solve the quadratic equation using the quadratic formula: ![]()
Show Solution
![]()
![]()
The Discriminant
The quadratic formula not only generates the solutions to a quadratic equation, it tells us about the nature of the solutions when we consider the discriminant, or the expression under the radical, ![]() The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. The table below relates the value of the discriminant to the solutions of a quadratic equation.
The discriminant tells us whether the solutions are real numbers or complex numbers, and how many solutions of each type to expect. The table below relates the value of the discriminant to the solutions of a quadratic equation.
| Value of Discriminant | Results |
|---|---|
| One rational solution (double solution) | |
| Two rational solutions | |
| Two irrational solutions | |
| Two complex solutions |
The Discriminant
For ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are real numbers, the discriminant is the expression under the radical in the quadratic formula:
are real numbers, the discriminant is the expression under the radical in the quadratic formula: ![]() It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.
It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to expect.
Using the Discriminant to Find the Nature of the Solutions to a Quadratic Equation
Use the discriminant to find the nature of the solutions to the following quadratic equations:
Show Solution
Calculate the discriminant ![]() for each equation and state the expected type of solutions.
for each equation and state the expected type of solutions.
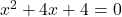
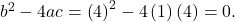 There will be one rational double solution.
There will be one rational double solution.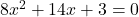
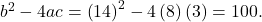 As
As 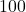 is a perfect square, there will be two rational solutions.
is a perfect square, there will be two rational solutions.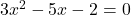
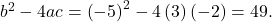 As
As 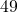 is a perfect square, there will be two rational solutions.
is a perfect square, there will be two rational solutions.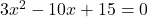
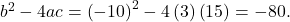 There will be two complex solutions.
There will be two complex solutions.
Access these online resources for additional instruction and practice with quadratic equations.
- Solving Quadratic Equations by Factoring
- The Zero-Product Property
- Quadratic Formula with Two Rational Solutions
Key Concepts
- Many quadratic equations can be solved by factoring when the equation has a leading coefficient of 1 or if the equation is a difference of squares. The zero-factor property is then used to find solutions.
- Many quadratic equations with a leading coefficient other than 1 can be solved by factoring using the grouping method.
- Another method for solving quadratics is the square root property. The variable is squared. We isolate the squared term and take the square root of both sides of the equation. The solution will yield a positive and negative solution.
- A highly dependable method for solving quadratic equations is the quadratic formula, based on the coefficients and the constant term in the equation.
- The discriminant is used to indicate the nature of the roots that the quadratic equation will yield: real or complex, rational or irrational, and how many of each.

