Learning Module 03B Graphs of Exponential Functions
Graphs of Exponential Functions
Learning Objectives
- Graph exponential functions.
- Graph exponential functions using transformations.
As we discussed in the previous section, exponential functions are used for many real-world applications such as finance, forensics, computer science, and most of the life sciences. Working with an equation that describes a real-world situation gives us a method for making predictions. Most of the time, however, the equation itself is not enough. We learn a lot about things by seeing their pictorial representations, and that is exactly why graphing exponential equations is a powerful tool. It gives us another layer of insight for predicting future events.
Graphing Exponential Functions
Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form ![]() whose base is greater than one. We’ll use the function
whose base is greater than one. We’ll use the function ![]() Observe how the output values in the table below change as the input increases by
Observe how the output values in the table below change as the input increases by ![]()
| |
|||||||
| |
Each output value is the product of the previous output and the base ![]() We call the base
We call the base ![]() the constant ratio. In fact, for any exponential function with the form
the constant ratio. In fact, for any exponential function with the form ![]()
![]() is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of
is the constant ratio of the function. This means that as the input increases by 1, the output value will be the product of the base and the previous output, regardless of the value of ![]()
Notice from the table that
- the output values are positive for all values of
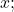
- as
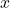 increases, the output values increase without bound; and
increases, the output values increase without bound; and - as
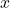 decreases, the output values grow smaller, approaching zero.
decreases, the output values grow smaller, approaching zero.
The graph below shows the exponential growth function ![]()
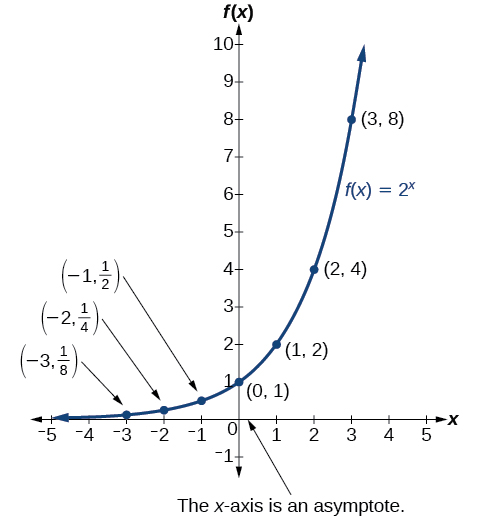
The domain of ![]() is all real numbers, the range is
is all real numbers, the range is ![]() and the horizontal asymptote is
and the horizontal asymptote is ![]()
To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form ![]() whose base is between zero and one. We’ll use the function
whose base is between zero and one. We’ll use the function ![]() Observe how the output values change as the input increases by
Observe how the output values change as the input increases by ![]()
| |
|||||||
Again, because the input is increasing by 1, each output value is the product of the previous output and the base, or constant ratio ![]()
Notice from the table that
- the output values are positive for all values of
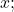
- as
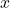 increases, the output values grow smaller, approaching zero; and
increases, the output values grow smaller, approaching zero; and - as
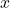 decreases, the output values grow without bound.
decreases, the output values grow without bound.
The graph below shows the exponential decay function ![]()
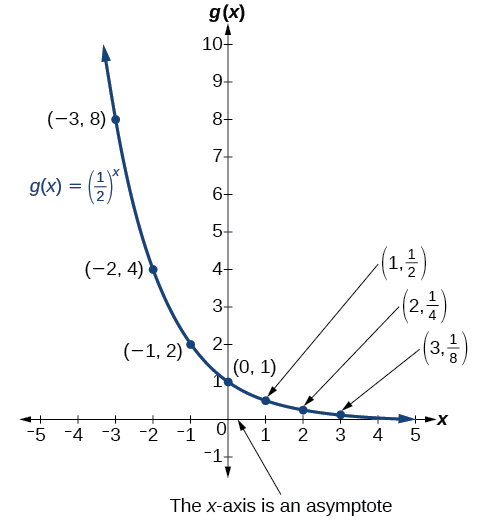
The domain of ![]() is all real numbers, the range is
is all real numbers, the range is ![]() and the horizontal asymptote is
and the horizontal asymptote is ![]()
Characteristics of the Graph of the Parent Function f(x) = bx
An exponential function with the form ![]()
![]()
![]() has these characteristics:
has these characteristics:
- one-to-one function
- horizontal asymptote:
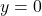
- domain:
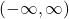
- range:
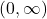
- x-intercept: none
- y-intercept:
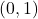
- increasing if
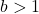
- decreasing if
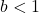
The graphs below compare the graphs of exponential growth and decay functions.

How To
Given an exponential function of the form ![]() graph the function.
graph the function.
- Create a table of points.
- Plot at least
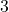 point from the table, including the y-intercept
point from the table, including the y-intercept 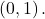
- Draw a smooth curve through the points.
- State the domain
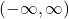 the range
the range 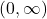 and the horizontal asymptote,
and the horizontal asymptote, 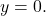
Sketching the Graph of an Exponential Function of the Form f(x) = bx
Sketch a graph of ![]() State the domain, range, and asymptote.
State the domain, range, and asymptote.
Show Solution
Before graphing, identify the behavior and create a table of points for the graph.
- Since
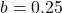 is between zero and one, we know the function is decreasing. The \left tail of the graph will increase without bound, and the right tail will approach the asymptote
is between zero and one, we know the function is decreasing. The \left tail of the graph will increase without bound, and the right tail will approach the asymptote 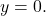
- Create a table of points.
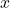
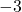
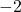
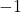
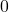
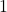
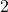
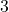
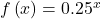
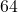
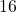
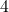
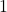
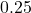
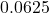
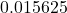
- Plot the y-intercept
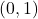 along with two other points. We can use
along with two other points. We can use 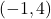 and
and 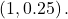
Draw a smooth curve connecting the points.

The domain is ![]() the range is
the range is ![]() the horizontal asymptote is
the horizontal asymptote is ![]()
Try It
Sketch the graph of ![]() State the domain, range, and asymptote.
State the domain, range, and asymptote.
Show Solution
The domain is ![]() the range is
the range is ![]() the horizontal asymptote is
the horizontal asymptote is ![]()

Graphing Transformations of Exponential Functions
Transformations of exponential graphs behave similarly to those of other functions. Just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function ![]() without loss of shape. For instance, just as the quadratic function maintains its parabolic shape when shifted, reflected, stretched, or compressed, the exponential function also maintains its general shape regardless of the transformations applied.
without loss of shape. For instance, just as the quadratic function maintains its parabolic shape when shifted, reflected, stretched, or compressed, the exponential function also maintains its general shape regardless of the transformations applied.
Graphing a Vertical Shift
The first transformation occurs when we add a constant ![]() to the parent function
to the parent function ![]() giving us a vertical shift
giving us a vertical shift ![]() units in the same direction as the sign. For example, if we begin by graphing a parent function
units in the same direction as the sign. For example, if we begin by graphing a parent function ![]() we can then graph two vertical shifts alongside it, using
we can then graph two vertical shifts alongside it, using ![]() the upward shift
the upward shift ![]() and the downward shift
and the downward shift ![]()

Observe the results of shifting ![]() vertically:
vertically:
- The domain
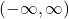 remains unchanged.
remains unchanged. - When the function is shifted up
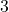 units to
units to 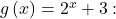
- The y-intercept shifts up
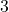 units to
units to 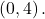
- The asymptote shifts up
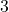 units to
units to 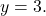
- The range becomes
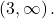
- The y-intercept shifts up
- When the function is shifted down
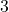 units to
units to 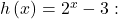
- The y-intercept shifts down
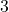 units to
units to 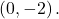
- The asymptote also shifts down
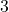 units to
units to 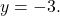
- The range becomes
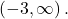
- The y-intercept shifts down
Graphing a Horizontal Shift
The next transformation occurs when we add a constant ![]() to the input of the parent function
to the input of the parent function ![]() giving us a horizontal shift
giving us a horizontal shift ![]() units in the opposite direction of the sign. For example, if we begin by graphing the parent function
units in the opposite direction of the sign. For example, if we begin by graphing the parent function ![]() we can then graph two horizontal shifts alongside it, using
we can then graph two horizontal shifts alongside it, using ![]() the shift left
the shift left ![]() and the shift right
and the shift right ![]() Both horizontal shifts are shown below.
Both horizontal shifts are shown below.

Observe the results of shifting ![]() horizontally:
horizontally:
- The domain
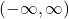 remains unchanged.
remains unchanged. - The asymptote
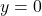 remains unchanged.
remains unchanged. - The y-intercept shifts such that:
- When the function is shifted left
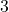 units to
units to 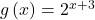 the y-intercept becomes
the y-intercept becomes 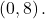 This is because
This is because 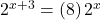 so the initial value of the function is
so the initial value of the function is 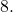
- When the function is shifted right
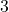 units to
units to 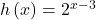 the y-intercept becomes
the y-intercept becomes 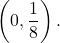 Again, see that
Again, see that 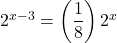 so the initial value of the function is
so the initial value of the function is 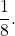
- When the function is shifted left
Shifts of the Parent Function f(x) = bx
For any constants ![]() and
and ![]() the function
the function ![]() shifts the parent function
shifts the parent function ![]()
- vertically
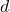 units, in the same direction of the sign of
units, in the same direction of the sign of 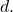
- horizontally
 units, in the opposite direction of the sign of
units, in the opposite direction of the sign of 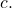
- The y-intercept becomes
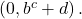
- The horizontal asymptote becomes
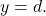
- The range becomes
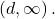
- The domain
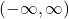 remains unchanged.
remains unchanged.
How To
Given an exponential function with the form ![]() graph the translation.
graph the translation.
- Draw the horizontal asymptote
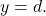
- Identify the shift as
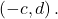 Shift the graph of
Shift the graph of 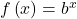 left
left  units if
units if  is positive, and right
is positive, and right  units if
units if  is negative.
is negative. - Shift the graph of
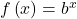 up
up 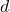 units if
units if 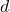 is positive, and down
is positive, and down 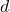 units if
units if 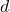 is negative.
is negative. - State the domain
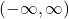 the range
the range 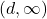 and the horizontal asymptote
and the horizontal asymptote 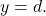
Graphing a Shift of an Exponential Function
Graph ![]() State the domain, range, and asymptote.
State the domain, range, and asymptote.
Show Solution
We have an exponential equation of the form ![]() with
with ![]()
![]() and
and ![]()
Draw the horizontal asymptote ![]() so draw
so draw ![]()
Identify the shift as ![]() so the shift is
so the shift is ![]()
Shift the graph of ![]() \left 1 units and down 3 units.
\left 1 units and down 3 units.
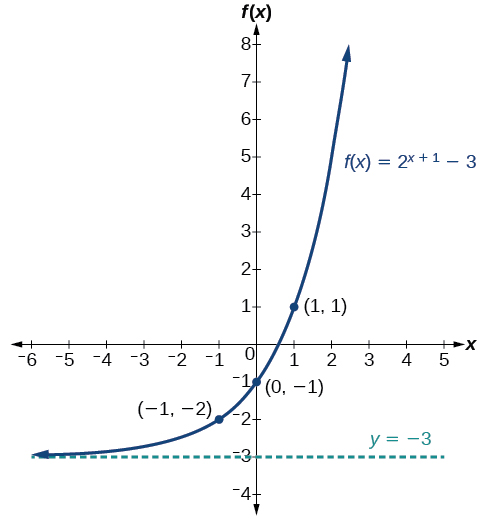
The domain is ![]() the range is
the range is ![]() the horizontal asymptote is
the horizontal asymptote is ![]()
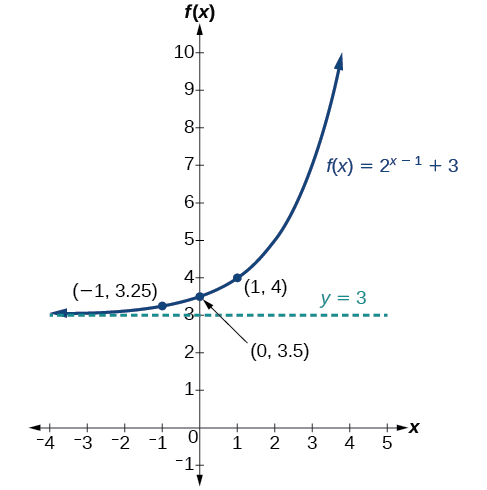
Try It
Graph ![]() State domain, range, and asymptote.
State domain, range, and asymptote.
Show Solution
The domain is ![]() the range is
the range is ![]() the horizontal asymptote is
the horizontal asymptote is ![]()
Try It
Solve ![]() graphically. Round to the nearest thousandth.
graphically. Round to the nearest thousandth.
Show Solution
![]()
Graphing a Stretch or Compression
While horizontal and vertical shifts involve adding constants to the input or to the function itself, a stretch or compression occurs when we multiply the parent function ![]() by a constant
by a constant ![]() For example, if we begin by graphing the parent function
For example, if we begin by graphing the parent function ![]() we can then graph the stretch, using
we can then graph the stretch, using ![]() to get
to get ![]() as shown on the left and the compression, using
as shown on the left and the compression, using ![]() to get
to get ![]() as shown on the right.
as shown on the right.

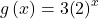 stretches the graph of
stretches the graph of 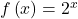 vertically by a factor of
vertically by a factor of 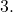 (b)
(b) 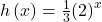 compresses the graph of
compresses the graph of 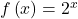 vertically by a factor of
vertically by a factor of 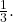
Stretches and Compressions of the Parent Function f(x) = bx
For any factor ![]() the function
the function ![]()
- is stretched vertically by a factor of
 if
if 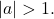
- is compressed vertically by a factor of
 if
if 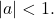
- has a y-intercept of
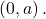
- has a horizontal asymptote at
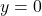 a range of
a range of 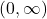 and a domain of
and a domain of 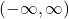 which are unchanged from the parent function.
which are unchanged from the parent function.
Graphing the Stretch of an Exponential Function
Sketch a graph of ![]() State the domain, range, and asymptote.
State the domain, range, and asymptote.
Show Solution
Before graphing, identify the behavior and key points on the graph.
- Since
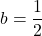 is between zero and one, the \left tail of the graph will increase without bound as
is between zero and one, the \left tail of the graph will increase without bound as 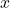 decreases, and the right tail will approach the x-axis as
decreases, and the right tail will approach the x-axis as 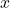 increases.
increases. - Since
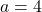 the graph of
the graph of 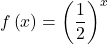 will be stretched by a factor of
will be stretched by a factor of 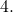
- Create a table of points.
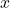
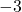
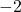
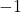
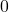
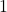
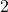
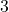
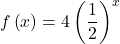
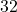
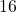
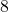
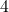
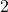
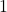
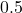
- Plot the y-intercept
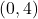 along with two other points. We can use
along with two other points. We can use 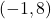 and
and 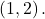
Draw a smooth curve connecting the points.

The domain is ![]() the range is
the range is ![]() the horizontal asymptote is
the horizontal asymptote is ![]()
Try It
Sketch the graph of ![]() State the domain, range, and asymptote.
State the domain, range, and asymptote.
Show Solution
The domain is ![]() the range is
the range is ![]() the horizontal asymptote is
the horizontal asymptote is ![]()

Key Equations
| General Form for the Translation of the Parent Function |
Key Concepts
- The graph of the function
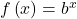 has a y-intercept at
has a y-intercept at 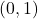 domain
domain 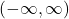 range
range 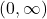 and horizontal asymptote
and horizontal asymptote 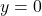 .
. - If
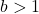 the function is increasing. The left tail of the graph will approach the asymptote
the function is increasing. The left tail of the graph will approach the asymptote 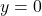 and the right tail will increase without bound.
and the right tail will increase without bound. - If
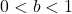 the function is decreasing. The left tail of the graph will increase without bound, and the right tail will approach the asymptote
the function is decreasing. The left tail of the graph will increase without bound, and the right tail will approach the asymptote 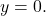
- The equation
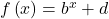 represents a vertical shift of the parent function
represents a vertical shift of the parent function 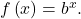
- The equation
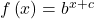 represents a horizontal shift of the parent function
represents a horizontal shift of the parent function 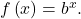
- Approximate solutions of the equation
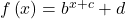 can be found using a graphing calculator.
can be found using a graphing calculator. - The equation
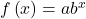 where
where 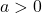 represents a vertical stretch if
represents a vertical stretch if 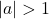 or compression if
or compression if 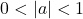 of the parent function
of the parent function 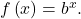
- When the parent function
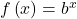 is multiplied by
is multiplied by 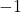 the result
the result 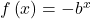 is a reflection about the x-axis. When the input is multiplied by
is a reflection about the x-axis. When the input is multiplied by 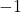 the result
the result 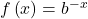 is a reflection about the y-axis.
is a reflection about the y-axis. - All translations of the exponential function can be summarized by the general equation
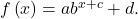
- Using the general equation
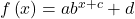 we can write the equation of a function given its description.
we can write the equation of a function given its description.

