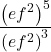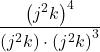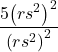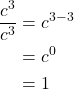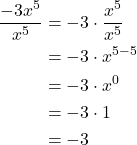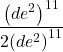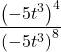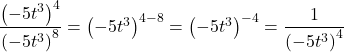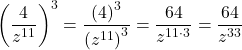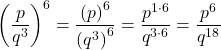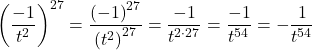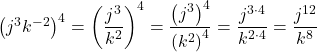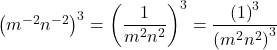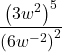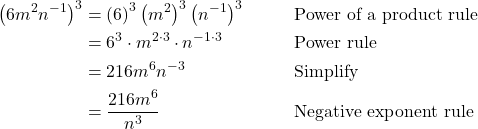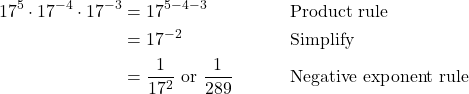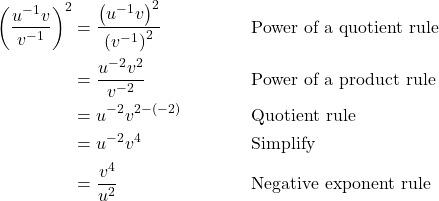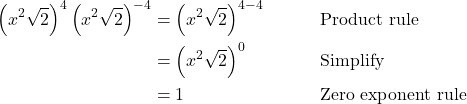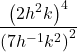Learning Module 03A Exponential Functions
Exponent Properties
Learning Objectives
In this section students will:
- Use the product rule of exponents.
- Use the quotient rule of exponents.
- Use the power rule of exponents.
- Use the zero exponent rule of exponents.
- Use the negative rule of exponents.
- Use the rational exponent rule of exponents.
- Find the power of a product and a quotient.
- Simplify exponential expressions.
Mathematicians, scientists, and economists commonly encounter very large and very small numbers. But it may not be obvious how common such figures are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is 2,048 pixels by 1,536 pixels, which is a very high resolution picture. It can also perceive a color depth (gradations in colors) of up to 48 bits per frame, and can shoot the equivalent of 24 frames per second. The maximum possible number of bits of information used to film a one-hour (3,600-second) digital film is then an extremely large number.
Using a calculator, we enter ![]() and press ENTER. The calculator displays 1.304596316E13. What does this mean? The “E13” portion of the result represents the exponent 13 of ten, so there are a maximum of approximately
and press ENTER. The calculator displays 1.304596316E13. What does this mean? The “E13” portion of the result represents the exponent 13 of ten, so there are a maximum of approximately ![]() bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
Using the Product Rule of Exponents
Consider the product ![]() . Both terms have the same base, x, but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
. Both terms have the same base, x, but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
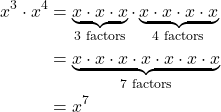
The result is that ![]() .
.
Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.
Now consider an example with real numbers.
We can always check that this is true by simplifying each exponential expression. We find that ![]() is 8
is 8 ![]() is 16, and
is 16, and ![]() is 128. The product
is 128. The product ![]() equals 128, so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.
equals 128, so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.
The Product Rule of Exponents
For any real number ![]() and natural numbers
and natural numbers ![]() and
and ![]() the product rule of exponents states that
the product rule of exponents states that
Using the Product Rule
Write each of the following products with a single base. Do not simplify further.
Show Solution
Use the product rule to simplify each expression.
At first, it may appear that we cannot simplify a product of three factors. However, using the associative property of multiplication, begin by simplifying the first two.
Notice we get the same result by adding the three exponents in one step.
Using the Quotient Rule of Exponents
The quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base but different exponents. In a similar way to the product rule, we can simplify an expression such as ![]() where
where ![]() . Consider the example
. Consider the example ![]() . Perform the division by canceling common factors.
. Perform the division by canceling common factors.
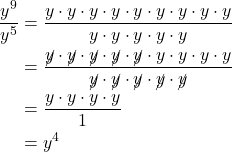
Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend.
In other words, when dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.
For the time being, we must be aware of the condition ![]() . Otherwise, the difference
. Otherwise, the difference ![]() could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.
could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.
The Quotient Rule of Exponents
For any real number ![]() and natural numbers
and natural numbers ![]() and
and ![]() such that
such that ![]() the quotient rule of exponents states that
the quotient rule of exponents states that
Using the Quotient Rule
Write each of the following products with a single base. Do not simplify further.
Show Solution
Use the quotient rule to simplify each expression.
Try It
Write each of the following products with a single base. Do not simplify further.
Show Solution
Using the Power Rule of Exponents
Suppose an exponential expression is raised to some power. Can we simplify the result? Yes. To do this, we use the power rule of exponents. Consider the expression ![]() . The expression inside the parentheses is multiplied twice because it has an exponent of 2. Then the result is multiplied three times because the entire expression has an exponent of 3.
. The expression inside the parentheses is multiplied twice because it has an exponent of 2. Then the result is multiplied three times because the entire expression has an exponent of 3.
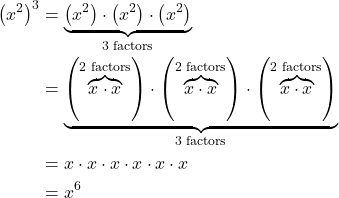
The exponent of the answer is the product of the exponents: ![]() .In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
.In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.
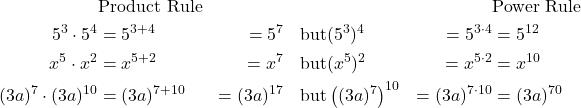
The Power Rule of Exponents
For any real number ![]() and positive integers
and positive integers ![]() and
and ![]() the power rule of exponents states that
the power rule of exponents states that
Using the Power Rule
Write each of the following products with a single base. Do not simplify further.
Show Solution
Use the power rule to simplify each expression.
Try It
Write each of the following products with a single base. Do not simplify further.
Show Solution
Using the Zero Exponent Rule of Exponents
Return to the quotient rule. We made the condition that ![]() so that the difference
so that the difference ![]() would never be zero or negative. What would happen if
would never be zero or negative. What would happen if ![]() ? In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
? In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
If we were to simplify the original expression using the quotient rule, we would have
If we equate the two answers, the result is ![]() . This is true for any nonzero real number, or any variable representing a real number.
. This is true for any nonzero real number, or any variable representing a real number.
The sole exception is the expression ![]() . This appears later in more advanced courses, but for now, we will consider the value to be undefined.
. This appears later in more advanced courses, but for now, we will consider the value to be undefined.
The Zero Exponent Rule of Exponents
For any nonzero real number ![]() the zero exponent rule of exponents states that
the zero exponent rule of exponents states that
Using the Zero Exponent Rule
Simplify each expression using the zero exponent rule of exponents.
Show Solution
Use the zero exponent and other rules to simplify each expression.
Try It
Simplify each expression using the zero exponent rule of exponents.
Show Solution
Using the Negative Rule of Exponents
Another useful result occurs if we relax the condition that ![]() in the quotient rule even further. For example, can we simplify
in the quotient rule even further. For example, can we simplify ![]() When
When ![]() —that is, where the difference
—that is, where the difference ![]() is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.
is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.
Divide one exponential expression by another with a larger exponent. Use our example ![]() .
.
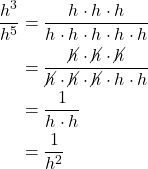
If we were to simplify the original expression using the quotient rule, we would have
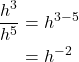
Putting the answers together, we have ![]() .This is true for any nonzero real number, or any variable representing a nonzero real number.
.This is true for any nonzero real number, or any variable representing a nonzero real number.
A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the \dfraction bar—from numerator to denominator or vice versa.
![]()
We have shown that the exponential expression ![]() is defined when
is defined when ![]() is a natural number, 0, or the negative of a natural number. That means that
is a natural number, 0, or the negative of a natural number. That means that ![]() is defined for any integer
is defined for any integer ![]() .Also, the product and quotient rules and all of the rules we will look at soon hold for any integer
.Also, the product and quotient rules and all of the rules we will look at soon hold for any integer ![]() .
.
The Negative Rule of Exponents
For any nonzero real number ![]() and natural number
and natural number ![]() the negative rule of exponents states that
the negative rule of exponents states that
Using the Negative Exponent Rule
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Try It
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Using the Product and Quotient Rules
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Try It
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
Show Solution
Finding the Power of a Product
To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents, which breaks up the power of a product of factors into the product of the powers of the factors. For instance, consider ![]() .We begin by using the associative and commutative properties of multiplication to regroup the factors.
.We begin by using the associative and commutative properties of multiplication to regroup the factors.
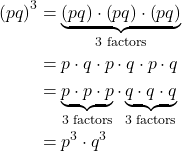
In other words ![]() .
.
The Power of a Product Rule of Exponents
For any real numbers ![]() and
and ![]() and any integer
and any integer ![]() the power of a product rule of exponents states that
the power of a product rule of exponents states that
Using the Power of a Product Rule
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
Show Solution
Use the product and quotient rules and the new definitions to simplify each expression.
Try It
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
Show Solution
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at the following example.
Let’s rewrite the original problem differently and look at the result.
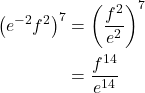
It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.
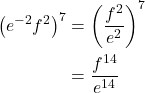
The Power of a Quotient Rule of Exponents
For any real numbers ![]() and
and ![]() and any integer
and any integer ![]() the power of a quotient rule of exponents states that
the power of a quotient rule of exponents states that
Using the Power of a Quotient Rule
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
Show Solution
Try It
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
Show Solution
Using Rational Exponents
Radical expressions can also be written without using the radical symbol. We can use rational (fractional) exponents. The index must be a positive integer. If the index ![]() is even, then
is even, then ![]() cannot be negative.
cannot be negative.
We can also have rational exponents with numerators other than 1. In these cases, the exponent must be a fraction in lowest terms. We raise the base to a power and take an nth root. The numerator tells us the power and the denominator tells us the root.
All of the properties of exponents that we learned for integer exponents also hold for rational exponents.
Rational Exponents
Rational exponents are another way to express principal nth roots. The general form for converting between a radical expression with a radical symbol and one with a rational exponent is
How To
Given an expression with a rational exponent, write the expression as a radical.
- Determine the power by looking at the numerator of the exponent.
- Determine the root by looking at the denominator of the exponent.
- Using the base as the radicand, raise the radicand to the power and use the root as the index.
Writing Rational Exponents as Radicals
Write ![]() as a radical. Simplify.
as a radical. Simplify.
Show Solution
The 2 tells us the power and the 3 tells us the root.
![]()
We know that ![]() because
because ![]() Because the cube root is easy to find, it is easiest to find the cube root before squaring for this problem. In general, it is easier to find the root first and then raise it to a power.
Because the cube root is easy to find, it is easiest to find the cube root before squaring for this problem. In general, it is easier to find the root first and then raise it to a power.
![]()
Try It
Write ![]() as a radical. Simplify.
as a radical. Simplify.
Show Solution
![]()
Writing Radicals as Rational Exponents
Write ![]() using a rational exponent.
using a rational exponent.
Show Solution
The index ![]() represents the denominator of the rational exponent. The
represents the denominator of the rational exponent. The ![]() represents the numerator of the rational exponent.
represents the numerator of the rational exponent.
![]() =
= ![]()
Try It
Write ![]() using a rational exponent.
using a rational exponent.
Show Solution
![]()
Simplifying Exponential Expressions
Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.
Simplifying Exponential Expressions
Simplify each expression and write the answer with positive exponents only.
Show Solution
Try It
Simplify each expression and write the answer with positive exponents only.
Show Solution
Access these online resources for additional instruction and practice with exponents and scientific notation.
Key Concepts
- Products of exponential expressions with the same base can be simplified by adding exponents.
- Quotients of exponential expressions with the same base can be simplified by subtracting exponents.
- Powers of exponential expressions with the same base can be simplified by multiplying exponents.
- An expression with exponent zero is defined as 1.
- An expression with a negative exponent is defined as a reciprocal.
- The power of a product of factors is the same as the product of the powers of the same factors.
- The power of a quotient of factors is the same as the quotient of the powers of the same factors.
- Radicals can be rewritten as rational exponents and rational exponents can be rewritten as radicals.
- The properties of exponents apply to rational exponents.
- The rules for exponential expressions can be combined to simplify more complicated expressions.